中考数学压轴题专题训练含答案解析 23页

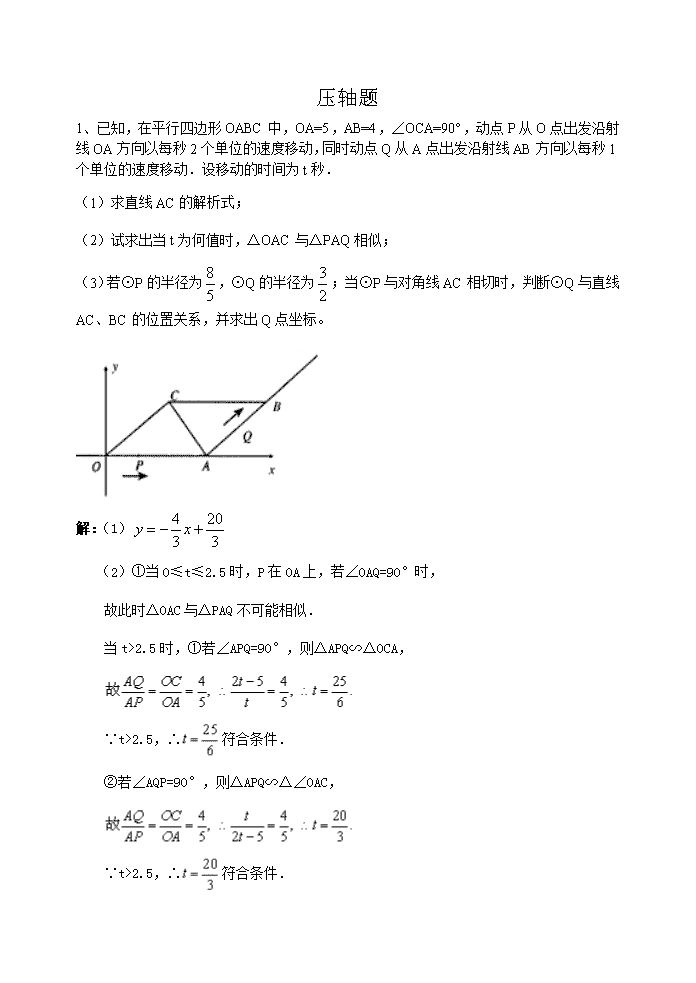
压轴题 ‎1、已知，在平行四边形OABC中，OA=5，AB=4，∠OCA=90°，动点P从O点出发沿射线OA方向以每秒2个单位的速度移动，同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动．设移动的时间为t秒．‎ ‎（1）求直线AC的解析式；‎ ‎（2）试求出当t为何值时，△OAC与△PAQ相似；‎ ‎（3）若⊙P的半径为，⊙Q的半径为；当⊙P与对角线AC相切时，判断⊙Q与直线AC、BC的位置关系，并求出Q点坐标。‎ 解：（1）‎ ‎（2）①当0≤t≤2.5时，P在OA上，若∠OAQ=90°时，‎ ‎　　故此时△OAC与△PAQ不可能相似．‎ ‎　　当t>2.5时，①若∠APQ=90°，则△APQ∽△OCA，‎ ‎　　‎ ‎　　∵t>2.5，∴符合条件．‎ ‎　　②若∠AQP=90°，则△APQ∽△∠OAC，‎ ‎　　‎ ‎　　∵t>2.5，∴符合条件．‎ ‎　　综上可知，当时，△OAC与△APQ相似．‎ ‎　　（3）⊙Q与直线AC、BC均相切，Q点坐标为（）。‎ ‎2、如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系．已知OA＝3，OC＝2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．‎ ‎（1）直接写出点E、F的坐标；‎ ‎（2）设顶点为F的抛物线交y轴正半轴于点P，且以点E、F、P为顶点的三角形是等腰三角形，求该抛物线的解析式；‎ ‎（第2题）‎ ‎（3）在x轴、y轴上是否分别存在点M、N，使得四边形MNFE的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由．‎ 解：（1）；．（2）在中，，‎ ‎．‎ 设点的坐标为，其中，顶点，‎ ‎∴设抛物线解析式为．‎ ‎①如图①，当时，，．‎ 解得（舍去）；．．．解得．‎ 抛物线的解析式为 ‎②如图②，当时，，．‎ 解得（舍去）．‎ ‎③当时，，这种情况不存在．‎ 综上所述，符合条件的抛物线解析式是．‎ ‎（3）存在点，使得四边形的周长最小．‎ 如图③，作点关于轴的对称点，作点关于 轴的对称点，连接，分别与轴、轴交于 点，则点就是所求点．‎ ‎，．‎ ‎．．又，，此时四边形的周长最小值是．‎ ‎3、如图，在边长为2的等边△ABC中，AD⊥BC,点P为边AB 上一个动点，过P点作PF//AC 交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设BP=x.‎ ‎（1）①试判断BG与2BP的大小关系,并说明理由;‎ ‎②用x的代数式表示线段DG的长,并写出自变量x的取值范围;‎ ‎（2）记△DEF的面积为S,求S与x之间的函数关系式,并求出S的最大值;‎ ‎（3）以P、E、F为顶点的三角形与△EDG是否可能相似？如果能相似，请求出BP的长，如果不能，请说明理由。‎ 第3题 解：（1）①在等边三角形ＡＢＣ中，∠Ｂ＝60°，∵ＰＧ⊥ＡＢ，‎ ‎　　　　　　∴∠ＢＧＰ＝30°，∴ＢＧ＝2ＢＰ．‎ ‎　　　　②∵ＰＦ／／ＡＣ，∴△ＰＢＦ为等边三角形，∴ＢＦ＝ＰＦ＝ＰＢ＝x.‎ 又∵ＢＧ＝2x，ＢＤ＝1，∴ＤＧ＝2x－1，∴０＜2x－1≤１，∴.‎ ‎（2）S=DE×DF=‎ ‎=‎ 当时，.‎ ‎（3）①如图１，若∠ＰＦＥ＝Ｒt∠，则两三角形相似，‎ 此时可得ＤＦ＝ＤＧ 即 解得：．‎ ‎②如图２，若∠ＰＥＦ＝Ｒt∠，则两三角形相似，‎ 此时可得ＤＦ＝ＥＦ＝ＢＰ，‎ 即．解得：．‎ ‎4、如图，二次函数的图像经过点，‎ 且与轴交于点.‎ ‎（1）试求此二次函数的解析式；‎ ‎（2）试证明：（其中是原点）；‎ ‎（3）若是线段上的一个动点（不与、重合），过作轴的平行线，分别交此二次函数图像及轴于、两点，试问：是否存在这样的点，使？若存在，请求出点的坐标；若不存在，请说明理由。‎ 解：（1）∵点与在二次函数图像上，‎ ‎∴，解得，‎ ‎∴二次函数解析式为.‎ ‎（2）过作轴于点，由（1）得，则在中，，又在中，， ‎ ‎∵，∴.‎ ‎（3）由与，可得直线的解析式为， ‎ 设，则，‎ ‎∴.∴.‎ 当，解得 （舍去），∴.‎ 当，解得 （舍去），∴.‎ 综上所述，存在满足条件的点，它们是与.‎ ‎5、如图1，在Rt△ABC中，∠C＝90°，BC＝8厘米，点D在AC上，CD＝3厘米．点P、Q分别由A、C两点同时出发，点P沿AC方向向点C匀速移动，速度为每秒k厘米，行完AC全程用时8秒；点Q沿CB方向向点B匀速移动，速度为每秒1‎ 厘米．设运动的时间为x秒，△DCQ的面积为y1平方厘米，△PCQ的面积为y2平方厘米．‎ ‎（1）求y1与x的函数关系，并在图2中画出y1的图象；‎ ‎（2）如图2，y2的图象是抛物线的一部分，其顶点坐标是（4，12），求点P的速度及AC的长；‎ ‎（3）在图2中，点G是x轴正半轴上一点（0＜OG＜6＝，过G作EF垂直于x轴，分别交y1、y2于点E、F．‎ ‎①说出线段EF的长在图1中所表示的实际意义；‎ 图2‎ G ‎2 4 6 8 10 ‎ ‎1210‎ ‎8‎ ‎6‎ ‎4‎ ‎2‎ y O x ‎②当0＜x＜６时，求线段EF长的最大值．‎ 图1‎ C Q→ B D A P↓‎ 解：（1）∵，CD＝3，CQ＝x，∴．‎ 图象如图所示．‎ ‎（2）方法一：，CP＝8k－xk，CQ＝x，‎ ‎∴．∵抛物线顶点坐标是（4，12），‎ ‎∴．解得．则点P的速度每秒厘米，AC＝12厘米．‎ 方法二：观察图象知，当x=4时，△PCQ面积为12．‎ 此时PC＝AC－AP＝8k－4k＝4k，CQ＝4．∴由，得 ．‎ 解得．则点P的速度每秒厘米，AC＝12厘米．‎ 方法三：设y2的图象所在抛物线的解析式是．‎ ‎∵图象过（0，0），（4，12），（8，0），‎ ‎∴ 解得 ∴． ①‎ ‎∵，CP＝8k－xk，CQ＝x，∴． ②‎ 比较①②得.则点P的速度每秒厘米，AC＝12厘米．‎ ‎（3）①观察图象，知线段的长EF＝y2－y1，表示△PCQ与△DCQ的面积差（或△PDQ面积）．②由⑵得 .（方法二，）‎ ‎∵EF＝y2－y1，∴EF＝，‎ ‎∵二次项系数小于０，∴在范围，当时，最大．‎ ‎6、如图，在中，，、分别是边、‎ 上的两个动点（不与、重合），且保持，以为边，在点的异侧作正方形.‎ ‎（1）试求的面积；‎ ‎（2）当边与重合时，求正方形的边长；‎ ‎（3）设，与正方形重叠部分的面积为，试求关于的函数关系式，并写出定义域；‎ ‎（4）当是等腰三角形时，请直接写出的长。‎ G F E D C B A 解：（1）过作于，∵，∴.‎ ‎ 则在中，，∴.‎ ‎（2）令此时正方形的边长为，则，解得.‎ ‎（3）当时，.‎ 当时，.‎ ‎ （4）.‎ ‎7、如图已知点A (-2，4) 和点B (1，0)都在抛物线上．‎ ‎（1）求、n；‎ ‎（2）向右平移上述抛物线，记平移后点A的对应点为A′，点B的对应点为B′，若四边形A A′B′B为菱形，求平移后抛物线的表达式；‎ ‎（3）记平移后抛物线的对称轴与直线AB′ 的交点为点C，试在轴上找点D，使得以点B′、C、D为顶点的三角形与相似．‎ 解：（1）根据题意，得： 解得 B A O ‎1‎ ‎1‎ ‎－1‎ ‎－1‎ x y A′‎ B′‎ ‎ （2）四边形A A′B′B为菱形，则A A′=B′B= AB=5‎ ‎ ∵‎ ‎ =‎ ‎∴ 向右平移5个单位的抛物线解析式为 ‎ ‎（3）设D（x，0）根据题意，得：AB=5，‎ ‎ ∵∠A=∠B B′A ‎ y B A O ‎1‎ ‎1‎ ‎－1‎ ‎－1‎ x C B′‎ D ⅰ) △ABC∽△B′CD时，∠ABC=∠B′CD ，∴BD=6－x， 由 得 解得x=3， ∴D（3，0）‎ ⅱ）△ABC∽△B′DC时，‎ ‎ ∴ 解得 ∴‎ ‎8、如 图，已知直角梯形ABCD中，AD∥BC，A B⊥BC ，AD＝2，AB＝8，‎ CD＝10．‎ ‎（1）求梯形ABCD的面积S；‎ ‎（2）动点P从点B出发，以1cm/s的速度、沿B→A→D→C方向，向点C运动；动点Q从点C出发，以1cm/s的速度、沿C→D→A方向，向点A运动，过点Q作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达目的地时整个运动随之结束，设运动时间为t秒．问：①当点P在B→A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值，并判断此时PQ是否平分梯形ABCD的面积；若不存在，请说明理由；‎ ‎②在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．‎ ‎（备用图）‎ 解：‎ 在Ｒt△DCH中，‎ ‎(2)①‎ 经计算，PQ不平分梯形ABCD的面积 ‎②‎ ‎，-‎ ‎9、如图，⊙O的半径为1，等腰直角三角形ABC的顶点B的坐标为（，0），CAB=90°，AC=AB，顶点A在⊙O上运动．‎ ‎（1）当点A在x轴上时，求点C的坐标；‎ ‎（2）当点A运动到x轴的负半轴上时，试判断直线BC与⊙O位置关系，并说明理由；‎ ‎（3）设点A的横坐标为x，△ABC的面积为S，求S与x之间的函数关系式，并求出S的最大值与最小值；‎ A B C O x y ‎（4）当直线AB与⊙O相切时，求AB所在直线对应的函数关系式．‎ 解：（1）当点A的坐标为（1，0）时，AB=AC=－1，点C的坐标为（1，－1）；‎ 当点A的坐标为（－1，0）时，AB=AC=＋1，点C的坐标为（－1，＋1）；‎ ‎（2）直线BC与⊙O相切，过点O作OM⊥BC于点M，∴∠OBM＝∠BOM=45°, ‎ ‎∴OM=OB·sin45°=1，∴直线BC与⊙O相切 ‎（3）过点A作AE⊥OB于点E 在Rt△OAE中，AE2=OA2－OE2=1－x2，‎ 在Rt△BAE中，AB2=AE2+BE2=(1-x2) +（-x）2=3-2x A B C O x y E ‎∴S=AB·AC= AB2=(3-2x)= ‎ 其中－1≤x≤1，‎ 当x=－1时，S的最大值为，‎ 当x=1时，S的最小值为．‎ ‎（4）①当点A位于第一象限时(如右图)：‎ 连接OA，并过点A作AE⊥OB于点E ‎∵直线AB与⊙O相切，∴∠OAB=90°，‎ A B ‎（C）‎ O x y E 又∵∠CAB=90°，∴∠CAB +∠OAB=180°，‎ ‎∴点O、A、C在同一条直线上，∴∠AOB=∠C=45°，‎ 在Rt△OAE中，OE=AE=．点A的坐标为（，）‎ 过A、B两点的直线为y=－x+．‎ ‎②当点A位于第四象限时(如右图)‎ 点A的坐标为（，－），过A、B两点的直线为y=x－． ‎ ‎10、已知抛物线y＝ax2＋bx＋c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OB