中考总复习整式与因式分解知识讲解基础 7页

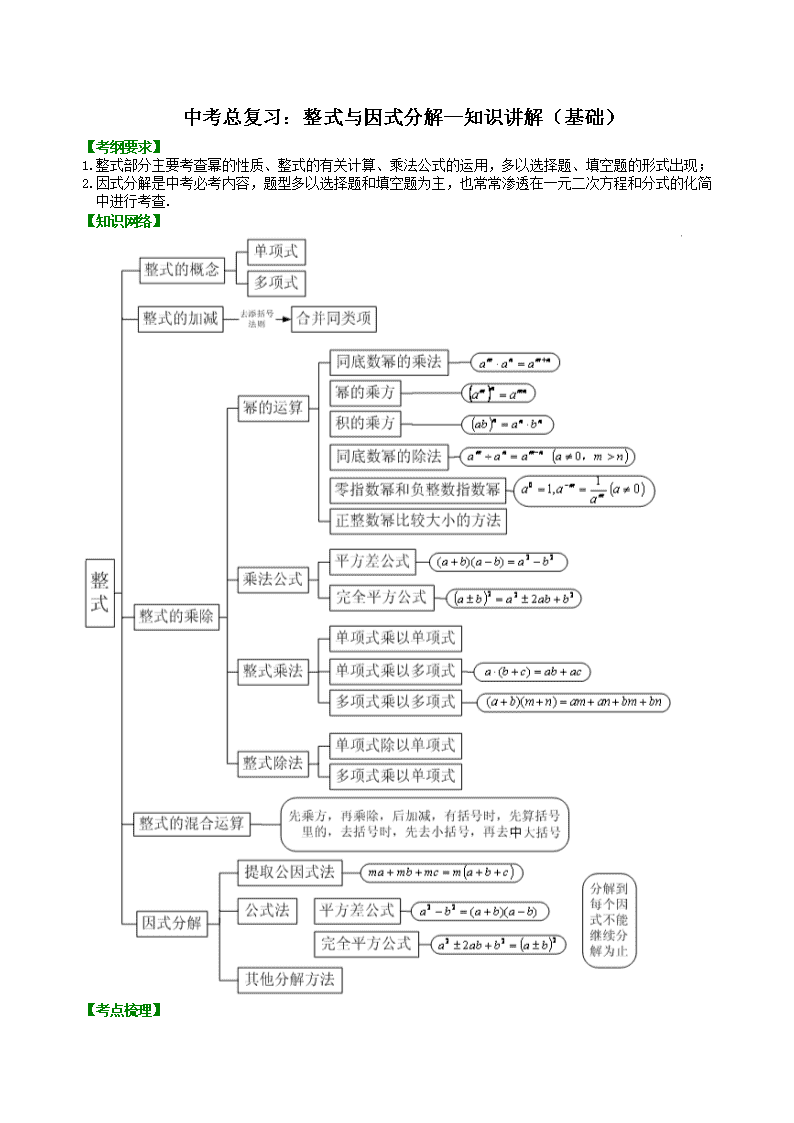
中考总复习：整式与因式分解—知识讲解（基础）‎ ‎【考纲要求】‎ ‎1.整式部分主要考查幂的性质、整式的有关计算、乘法公式的运用，多以选择题、填空题的形式出现；‎ ‎2.因式分解是中考必考内容，题型多以选择题和填空题为主，也常常渗透在一元二次方程和分式的化简中进行考查.‎ ‎【知识网络】‎ ‎【考点梳理】‎ 考点一、整式 1.单项式 　　数与字母的积的形式的代数式叫做单项式．单项式是代数式的一种特殊形式，它的特点是对字母来说只含有乘法的运算，不含有加减运算．在含有除法运算时，除数(分母)只能是一个具体的数，可以看成分数因数．单独一个数或一个字母也是单项式．‎ 要点诠释：‎ ‎（1）单项式的系数是指单项式中的数字因数．‎ ‎（2）单项式的次数是指单项式中所有字母的指数和．‎ ‎2.多项式 　　几个单项式的代数和叫做多项式．也就是说，多项式是由单项式相加或相减组成的．‎ 要点诠释：‎ ‎（1）在多项式中，不含字母的项叫做常数项．‎ ‎（2）多项式中次数最高的项的次数，就是这个多项式的次数．‎ ‎（3）多项式的次数是n次，有m个单项式，我们就把这个多项式称为n次m项式．‎ ‎ （4）把一个多项式按某一个字母的指数从大到小的顺序排列起来，叫做把这个多项式按这个字母降幂排列．另外，把一个多项式按某一个字母的指数从小到大的顺序排列起来，叫做把这个多项式按这个字母升幂排列．‎ ‎3.整式 　　单项式和多项式统称整式． 4.同类项 　　所含字母相同，并且相同字母的指数也分别相同的项，叫做同类项． 5.整式的加减 　　整式的加减其实是去括号法则与合并同类项法则的综合运用． 　　把多项式中的同类项合并成一项，叫做合并同类项.合并同类项后，所得项的系数是合并前各同类项的系数的和，且字母部分不变. 　　如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同；如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反. 　　整式加减的运算法则：一般地，几个整式相加减，如果有括号就先去括号，然后再合并同类项. 6.整式的乘除 　　①幂的运算性质： 　　　 　　②单项式相乘：两个单项式相乘，把系数、相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式． 　　③单项式与多项式相乘：单项式与多项式相乘，用单项式去乘多项式的每一项，再把所得的积相加．用式子表达： 　　④多项式与多项式相乘：一般地，多项式乘以多项式，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加．用式子表达： 　　　平方差公式：‎ 完全平方公式： 　　　 　　　在运用乘法公式计算时，有时要在式子中添括号，添括号时，如果括号前面是正号，括到括号里的各项都不变符号；如果括号前面是负号，括到括号里的各项都改变符号. 　　⑤单项式相除：两个单项式相除，把系数与同底数幂分别相除作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式． 　　⑥多项式除以单项式：多项式除以单项式，先把这个多项式的每一项除以这个单项式，再把所得的商相加． ‎ 要点诠释：‎ ‎（1）同底数幂是指底数相同的幂，底数可以是任意的有理数，也可以是单项式、多项式.‎ ‎（2）三个或三个以上同底数幂相乘时，也具有这一性质， ‎ 即（都是正整数）. ‎ ‎（3）公式的推广： (，均为正整数)‎ ‎ （4）公式的推广： (为正整数).‎ 考点二、因式分解 ‎1.因式分解 　　 把一个多项式化成几个整式的积的形式，这样的式子变形叫做把这个多项式因式分解． 2.因式分解常用的方法 ‎ （1）提取公因式法：‎ ‎ （2）运用公式法：‎ 平方差公式：；完全平方公式：‎ ‎（3）十字相乘法：‎ ‎3.因式分解的一般步骤 ‎（1）如果多项式的各项有公因式，那么先提公因式；‎ ‎（2）提出公因式或无公因式可提，再考虑可否运用公式或十字相乘法；‎ ‎（3）对二次三项式，应先尝试用十字相乘法分解，不行的再用求根公式法；‎ ‎（4）最后考虑用分组分解法及添、拆项法.‎ 要点诠释：‎ ‎（1）因式分解的对象是多项式；‎ ‎（2）最终把多项式化成乘积形式；‎ ‎（3）结果要彻底，即分解到每个因式都不能再分解为止．‎ ‎（4）十字相乘法分解思路为“看两端，凑中间”，二次项系数一般都化为正数，如果是负数，则提出负号，分解括号里面的二次三项式，最后结果不要忘记把提出的负号添上.‎ ‎【典型例题】‎ 类型一、整式的有关概念及运算 ‎ ‎1．若3xm+5y2与x3yn的和是单项式，则nm ．‎ ‎【答案】‎ ‎【解析】由3xm+5y2与x3yn的和是单项式得3xm+5y2与x3yn是同类项，‎ ‎∴ 解得 ， nm=2-2= ‎ ‎【点评】本题考查同类项定义结合求解二元一次方程组，负整数指数幂的计算. 　　 同类项的概念为：所含字母相同，并且相同字母的指数也相同的单项式. 举一反三：‎ ‎【变式】若单项式是同类项，则的值是( 　)‎ ‎ 　A、-3 　　　B、‎-1　　‎　 C、 　　　D、3‎ ‎【答案】由题意单项式是同类项， 　　　 　所以，解得 ，，应选C.‎ ‎2．下列各式中正确的是( 　) 　　 A. 　　　B.a2·a3=a‎6　　‎　 C.(‎-3a2)3=‎-9a6 　　　D.a5+a3=a8 　　‎ ‎【答案】A； 【解析】选项B为同底数幂乘法，底数不变，指数相加，a2·a3=a5，所以B错；‎ 选项C为积的乘方，应把每个因式分别乘方，再把所得的幂相乘，(-‎3a2)3=-‎27a6，所以C错；选项D为两个单项式的和，此两项不是同类项，不能合并，所以D错；‎ 选项A为负指数幂运算，一个数的负指数幂等于它的正指数幂的倒数，A正确.答案选A. ‎ ‎【点评】考查整数指数幂运算.‎ 举一反三：‎ ‎【变式1】下列运算正确的是 ( )‎ A．         B．         C．     D．‎ ‎【答案】A.2-3 = ； B. ；C. 正确 ；D.. 故选C.‎ ‎【高清课程名称： 整式与因式分解 高清ID号：399488‎ 关联的位置名称（播放点名称）：例1-例2】‎ ‎【变式2】下列运算中，计算结果正确的个数是( )．‎ ‎(1)a4·a3＝a12； (2)a6÷a3＝a2； (3)a5＋a5＝a10；‎ ‎(4)(a3)2＝a9； (5)(－ab2)2＝ab4； (6)‎ A．无 B．1个 C．2个 D．3个 ‎【答案】A.‎ ‎3．利用乘法公式计算： 　 　(1)(a+b+c)2 (2)(‎2a2-3b2+2)(2‎-2a2+3b2)‎ ‎【答案与解析】‎ ‎(1)(a+b+c)2可以利用完全平方公式，将a+b看成一项，则 　　　　(a+b+c)2=[(a+b)2+2(a+b)c+c2] 　　　　　 　=a2+2ab+b2+‎2ac+2bc+c2 　　　　　 =a2+b2+c2+2ab+‎2ac+2bc. 　　 (2)(‎2a2-3b2+2)(2‎-2a2+3b2)两个多项式中，每一项都只有符号的区别，所以，我们考虑用平方差公 式，将符号相同的看作公式中的a，将符号相反的项，看成公式中的b， 　　原式=[2+(‎2a2-3b2)][2-(‎2a2-3b2)] 　　 =4-(‎2a2-3b2)2=4‎-4a4+‎12a2b2-9b4. 【点评】利用乘法公式去计算时，要特别注意公式的形式及符号特点，灵活地进行各种变形.‎ 举一反三：‎ ‎【变式】如果a2+ma+9是一个完全平方式，那么m=______.‎ ‎【答案】利用完全平方公式：(a±3)2=a2±‎6a+9. m=±6.‎ 类型二、因式分解 ‎4．因式分解：①‎3a3‎-6a2+‎12a； ②(a+b)2-1； ③x2-12x+36； ④(a2+b2)2‎-4a2b2 　　‎ ‎【答案与解析】‎ ‎① ‎3a3‎-6a2+‎12a=‎3a(a2‎-2a+4) 　　　 ② (a+b)2-1=(a+b)2-12=[(a+b)+1][(a+b)-1]=(a+b+1)(a+b-1) 　　　 ③ x2-12x+36=(x-6)2 　　 ④ (a2+b2)2‎-4a2b2=(a2+b2-2ab)(a2+b2+2ab)=(a-b)2(a+b)2‎ ‎【点评】把一个多项式进行因式分解，首先要看多项式是否有公因式，有公因式就要先提取公因式，再看是否还可以继续进行分解，是否可以利用公式法进行分解，直到不能进行分解为止.‎ 举一反三：‎ ‎【高清课程名称： 整式与因式分解 高清ID号：399488‎ 关联的位置名称（播放点名称）：例3（1）-（2）】‎ ‎【变式】把下列各式分解因式：‎ ‎(1)6(a－b)2＋‎8a(b－a)； (2)(x＋y)2－4(x＋y)＋4.‎ ‎【答案】‎ ‎(1)原式＝6(a－b)2－‎8a(a－b)‎ ‎＝2(a－b)[3(a－b)－‎4a]‎ ‎＝2(a－b)(‎3a－3b－‎4a)‎ ‎＝－2(a－b)(a＋3b)．‎ ‎(2)原式＝[(x＋y)－2]2＝(x＋y－2)2．‎ ‎5．若能分解为两个一次因式的积，则m的值为（ ）‎ ‎ A. 1 B. ‎-1 ‎ C. D. 2‎ ‎【思路点拨】‎ ‎ 对二元二次多项式分解因式时，要先观察其二次项能否分解成两个一次式乘积，再通过待定系数法确定其系数，这是一种常用的方法.‎ ‎【答案】C.‎ ‎【解析】‎ 解：‎ ‎ -6可分解成或，因此，存在两种情况：‎ ‎ ‎ 由（1）可得：，‎ 由（2）可得：.‎ ‎ 故选择C.‎ ‎ ‎ ‎【总结升华】十字相乘法分解思路为“看两端，凑中间”，二次项系数一般都化为正数，如果是负数，则提出负号，分解括号里面的二次三项式，最后结果不要忘记把提出的负号添上.‎ 举一反三：‎ ‎【变式】因式分解：_______________.‎ ‎【答案】‎ 类型三、因式分解与其他知识的综合运用 ‎6．已知a、b、c 是△ABC的三边的长,且满足: a2+2b2+c2-2b(a+c)=0,试判断此三角形的形状.‎ ‎【思路点拨】‎ ‎ 式子a2+2b2+c2-2b(a+c)=0体现了三角形三边长关系，从形式上看与完全平方式相仿，把2b2写成b2+b2‎ ‎，故等式可变成2个完全平方式，从而得到结论．‎ ‎【答案与解析】 ‎ 解: a2+2b2+c2-2b(a+c)=0 ‎ ‎ a2+b2+ b2+c2-2ba-2bc=0‎ ‎ (a-b) 2+(b-c) 2=0 ‎ 即: a-b=0 , b-c=0，所以a=b=c.‎ 所以△ABC是等边三角形.‎ ‎【总结升华】通过对式子变化，化为平方和等于零的形式，从而求出三边长的关系．‎