中考几何证明题集锦主要是与圆有关的 6页

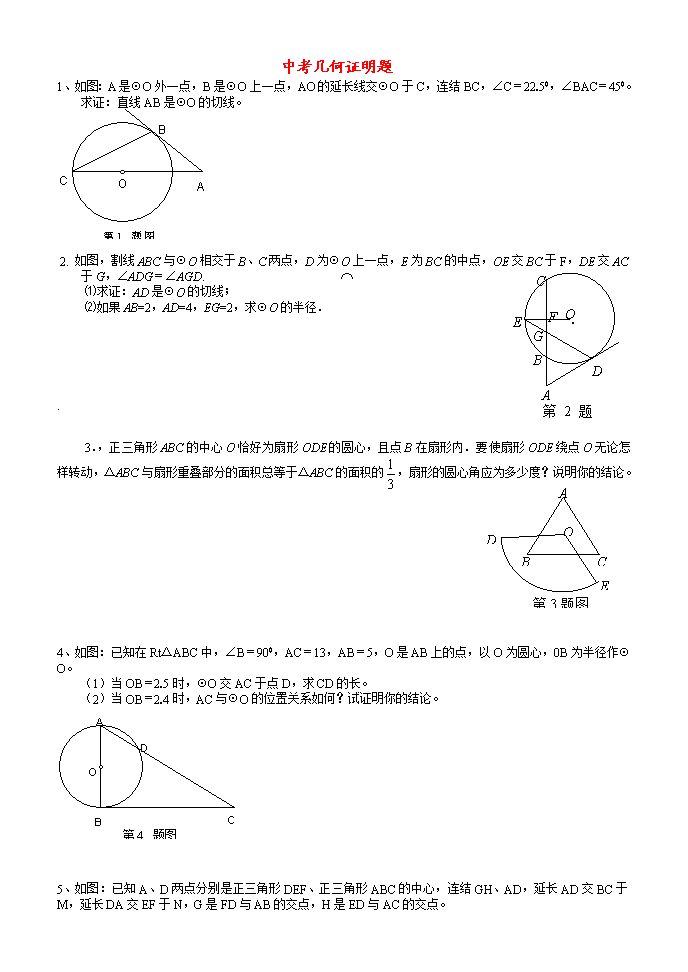
中考几何证明题 ‎1、如图：A是⊙O外一点，B是⊙O上一点，AO的延长线交⊙O于C，连结BC，∠C＝22.50，∠BAC＝450。求证：直线AB是⊙O的切线。‎ ‎ ‎ 第2题图 A ‎ ‎ ‎ D C E F G B O ‎·‎ ‎ 2. ‎⌒‎ 如图，割线ABC与⊙O相交于B、C两点，D为⊙O上一点，E为BC的中点，OE交BC于F，DE交AC于G，∠ADG＝∠AGD.‎ ‎⑴求证：AD是⊙O的切线；‎ ‎⑵如果AB=2，AD=4，EG=2，求⊙O的半径．‎ ‎. ‎ D A O B C E 第3题图 ‎3．，正三角形ABC的中心O恰好为扇形ODE的圆心，且点B在扇形内．要使扇形ODE绕点O无论怎样转动，△ABC与扇形重叠部分的面积总等于△ABC的面积的，扇形的圆心角应为多少度？说明你的结论。‎ ‎ ‎ ‎ ‎ ‎4、如图：已知在Rt△ABC中，∠B＝900，AC＝13，AB＝5，O是AB上的点，以O为圆心，0B为半径作⊙O。‎ ‎ （1）当OB＝2.5时，⊙O交AC于点D，求CD的长。‎ ‎ （2）当OB＝2.4时，AC与⊙O的位置关系如何？试证明你的结论。‎ ‎5、如图：已知A、D两点分别是正三角形DEF、正三角形ABC的中心，连结GH、AD，延长AD交BC于M，延长DA交EF于N，G是FD与AB的交点，H是ED与AC的交点。‎ ‎（1）写出三个不同类型的、必须经过至少两步推理才能得到的正确结论（不要求写出证明过程）；‎ ‎（2）问FE、GH、BC有何位置关系？试证明你的结论。‎ ‎ ‎ ‎6．如图（a），已知直线AB过圆心O，交⊙O于A、B，直线AF交⊙O于F ‎（不与B重合），直线l交⊙O于C、D，交AB于E，且与AF垂直，垂足为G，连结AC、AD．‎ 求证：①∠BAD＝∠CAG；②AC·AD＝AE·AF．‎ ‎（2）在问题（1）中，当直线l向上平行移动，与⊙O相切时，其他条件不变．‎ ‎①请你在图（b）中画出变化后的图形，并对照图（a），标记字母；‎ ‎②问题（1）中的两个结论是否成立？如果成立，请给出证明；如果不成立，请说明理由． ‎ 图(a)‎ B O A F D C G E l ‎·‎ B O A 图(b)‎ 第6题图 ‎·‎ ‎·‎ B D C F E A G O ‎7． 如图，△ABC中，∠BAC的平分线AD交BC于D，⊙O过点A，且和BC切于D，和AB、AC分别交于E、F。设EF交AD于G ，连结DF。‎ （1） 求证：EF∥BC ；‎ （2） 已知：DF =2 ，AG =3 ，求的值。‎ ‎8、 已知：如图，CD是Rt△ABC的斜边AB上的高，且BC＝，AB＝，CD＝，AD＝，DB＝。求证：，‎ ‎9、 已知：如图，线段AM∥DN，直线与AM、DN分别交于点B、C，直线绕BC的中点P旋转（点C由D点向N点方向移动）。‎ ‎（1）线段BC与AD、AB、CD围成的图形，在初始状态下，形状是△ABD，（即△ABC ‎），请你写出变化过程中其余的各种特殊四边形名称；（5分）‎ ‎（2）任取变化过程中的两个图形，测量AB、CD长度后分别计算同一个图形的AB＋CD（精确到1cm），比较这两个和是否相同，试加以证明。（7分）‎ ‎10、 ‎ 已知：如图，边长为2的正五边形ABCDE内接于⊙O，AB、DC的延长线交于点F，过点E作EG∥CB交BA的延长线于点G。‎ ‎（1）求证：（6分）‎ ‎（2）证明：EG与⊙O相切，并求AG、BF的长。（6分）‎ ‎11． 如图9，已知△ABC内接于⊙O，直线DE与⊙O相切于点A．BD∥CA．‎ ‎ 求证：AB·DA＝BC·BD．‎ ‎12. 已知△ABC中，AC＝5，BC＝12，∠ACB＝90°，P是AB边上的动点（与点A、B不重合）Q是BC边上的动点（与点B、C不重合）． （1）如图10，当PQ∥AC，且Q为BC的中点时，求线段CP的长； （2）当PQ与AC不平行时，△CPQ可能为直角三角形吗？若有可能，请求出线段CQ的长的取值范围；若不可能，请说明理由．‎ ‎13、如图10是线段AB上一点，△APC与△BPD是等边三角形，请你判断AD与BC相等吗？并证明你的判断。‎ ‎14、如图11，已知E是△ABC的内心，∠A的平分线交BC于点F，且与△ABC的外接回相交于点D。‎ ‎（1）求证：∠DBE＝∠DEB；‎ ‎（2）若AD＝8cm，DF∶FA＝1∶3。求DE的长。‎ ‎ ‎ ‎15. 将正方形ABCD绕点A按逆时针方向旋转（00