中考数学几何最值专题 8页

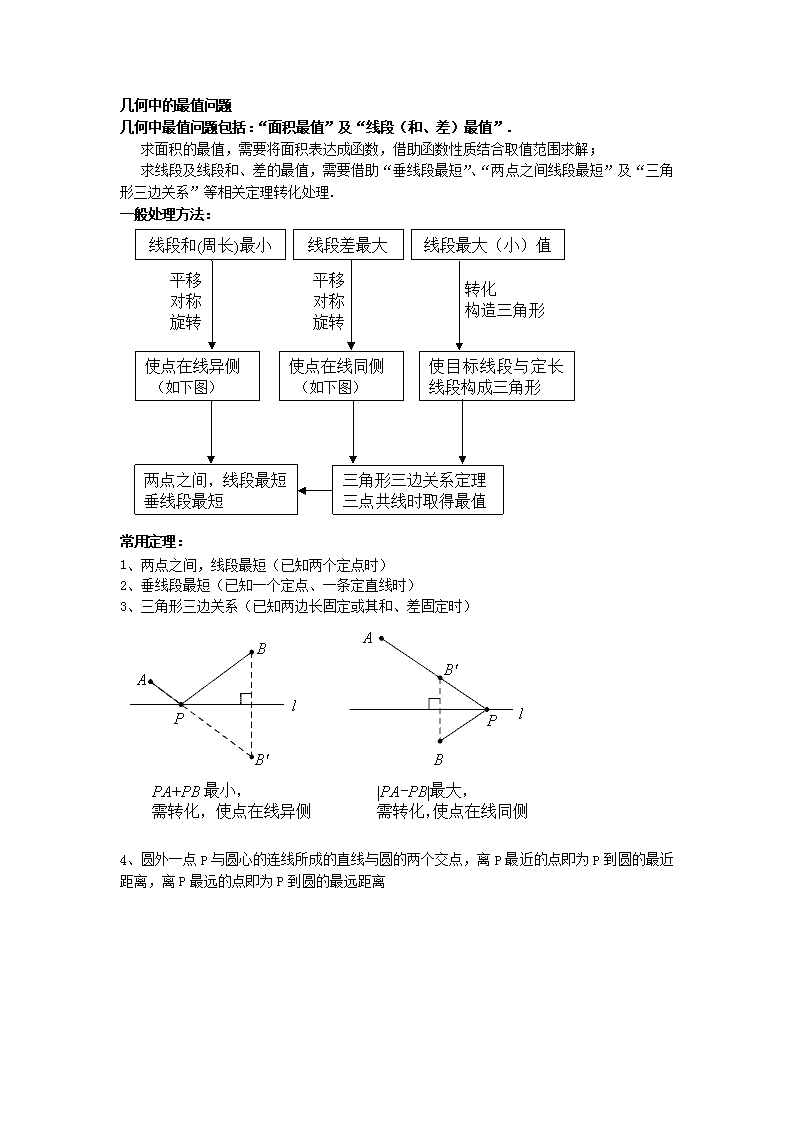
几何中的最值问题 几何中最值问题包括：“面积最值”及“线段（和、差）最值”.‎ ‎ 求面积的最值，需要将面积表达成函数，借助函数性质结合取值范围求解；‎ ‎ 求线段及线段和、差的最值，需要借助“垂线段最短”、“两点之间线段最短”及“三角形三边关系”等相关定理转化处理.‎ 一般处理方法：‎ 线段最大（小）值 线段差最大 线段和(周长)最小 平移 对称 旋转 平移 对称 旋转 转化 构造三角形 使目标线段与定长线段构成三角形 使点在线同侧 ‎（如下图）‎ 使点在线异侧 ‎（如下图）‎ 三角形三边关系定理 三点共线时取得最值 两点之间，线段最短 垂线段最短 常用定理：‎ ‎1、两点之间，线段最短（已知两个定点时）‎ ‎2、垂线段最短（已知一个定点、一条定直线时）‎ ‎3、三角形三边关系（已知两边长固定或其和、差固定时）‎ ‎|PA-PB|最大，‎ 需转化，使点在线同侧 PA+PB最小，‎ 需转化，使点在线异侧 ‎ ‎ ‎ ‎ 4、 圆外一点P与圆心的连线所成的直线与圆的两个交点，离P最近的点即为P到圆的最近距离，离P最远的点即为P到圆的最远距离 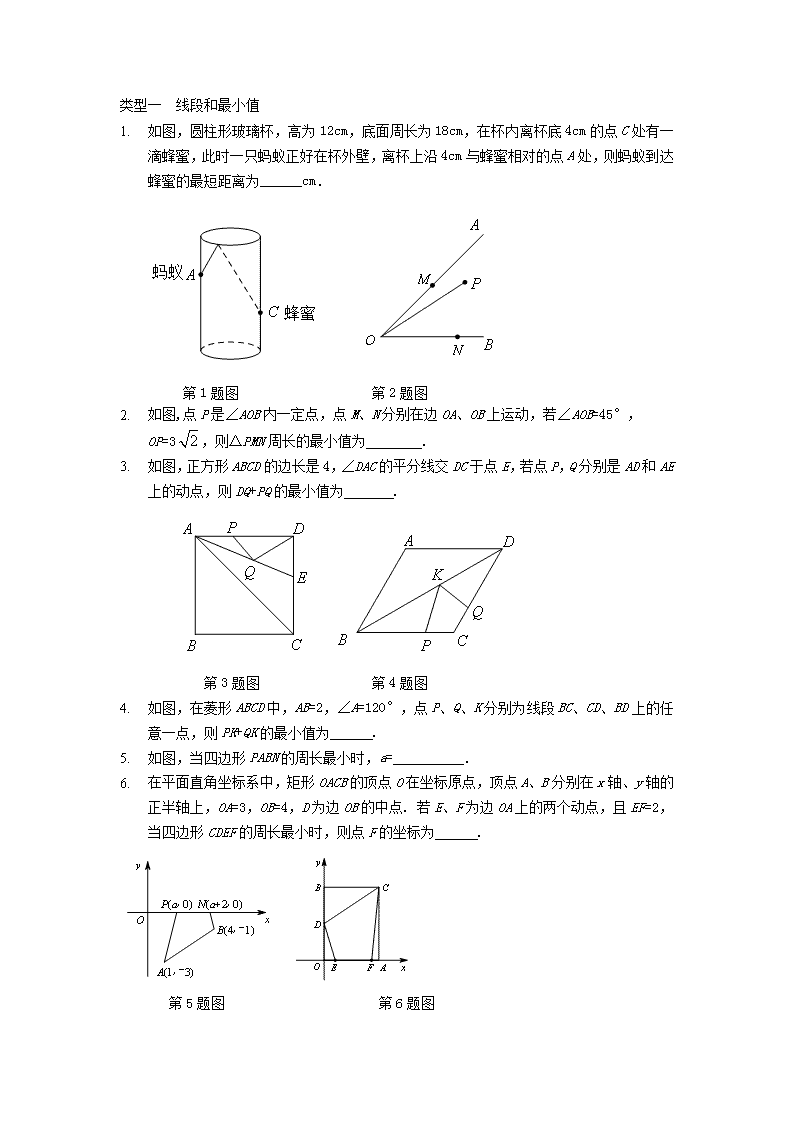类型一 线段和最小值 1. 如图，圆柱形玻璃杯，高为12cm，底面周长为18cm，在杯内离杯底4cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为______cm．‎ ‎ ‎ ‎ 第1题图 第2题图 2. 如图,点P是∠AOB内一定点，点M、N分别在边OA、OB上运动，若∠AOB=45°，OP=3，则△PMN周长的最小值为 . ‎ 3. 如图，正方形ABCD的边长是4，∠DAC的平分线交DC于点E，若点P，Q分别是AD和AE上的动点，则DQ+PQ的最小值为 .‎ ‎ ‎ ‎ 第3题图 第4题图 4. 如图，在菱形ABCD中，AB=2，∠A=120°，点P、Q、K分别为线段BC、CD、BD上的任意一点，则PK+QK的最小值为 .‎ 5. 如图，当四边形PABN的周长最小时，a= ．‎ 6. 在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点. 若E、F为边OA上的两个动点，且EF=2，当四边形CDEF的周长最小时，则点F的坐标为 .‎ ‎ ‎ ‎ 第5题图 第6题图 变式加深：‎ ‎1、如图,正方形ABCD边长为2,当点A在x轴上运动时,点D随之在y轴上运动,在运动过程中,点B到原点O的最大距离为()‎ A. B. C. D. ‎ ‎2、如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在边OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为 ‎ ‎3、如图，E、F是正方形ABCD的边AD上的两个动点，满足AE=DF，连接CF交BD于点G,连接BE交AG与点H。若正方形的边长为2，则线段DH长度的最小值是 ‎ ‎4、如图，点P在第一象限，△ABP是边长为2的等边三角形，当点A在x轴的正半轴上运动时，点B随之在y轴的正半轴上运动，运动过程中，点P到原点的最大距离是________.若将△ABP中边PA的长度改为，另两边长度不变，则点P到原点的最大距离变为_________．‎ 类型二 线段差最大值 ‎1、如图，两点A、B在直线MN外的同侧，A到MN的距离AC=8，B到MN的距离BD=5，CD=4，P在直线MN上运动，则的最大值等于 ． ‎ ‎ 2、点A、B均在由面积为1的相同小矩形组成的网格的格点上，建立平面直角坐标系如图所 示．若P是x轴上使得的值最大的点，Q是y轴上使得QA+QB的值最小的点，则＝　　　　　　．‎ ‎3、如图所示,已知A(,y1),B(2,y2)为反比例函数y=图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )‎ A. B.(1,0) C. D. ‎ ‎ ‎ ‎4、一次函数y1=kx-2与反比例函数y2=（m<0）的图象交于A，B两点，其中点A的坐标为（-6，2）‎ ‎（1）求m，k的值；‎ ‎（2）点P为y轴上的一个动点，当点P在什么位置时|PA-PB|‎ 的值最大？并求出最大值.‎ 核心：画曲为直 ‎1、已知如图，圆锥的底面圆的半径为1，母线长OA为2，C为母线OB的中点．在圆锥的侧面上，一只蚂蚁从点A爬行到点C的最短线路长为 ．‎ ‎2、如图，圆柱底面半径为，高为，点A、B分别是圆柱两底面圆周上的点，且A、B在同一母线上，用一棉线从A顺着圆柱侧面绕3圈到B，求棉线最短为 。‎ ‎3、在锐角三角形ABC中，BC=，∠ABC=45°，BD平分∠ABC，M、N分别是BD、BC上的动点，则CM+MN的最小值是 ‎ O C B A 类型三 线段最值 ‎1、已知⊙O是以原点为圆心，为半径的圆，点P是直线上的一点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为________ ‎ ‎2、在平面直角坐标系xOy中，以原点O为圆心的圆过点A（13,0），直线y=kx-3k+4与圆O交于B、C两点，则弦BC的长的最小值为______________.‎ ‎3、如图，在△ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为_________．‎ ‎4、如图，已知AB=10，P是线段AB上任意一点，在AB的同侧分别以AP和PB为边作等边△APC和等边△BPD，则CD长度的最小值为 ．‎ ‎5、如图，在△ABC中，∠BAC=120°，AB=AC=4，M、N两点分别是边AB、AC上的动点，将△AMN沿MN翻折，A点的对应点为A′，连接BA′，则BA′的最小值是_________．‎ ‎6、如图，一副三角板拼在一起，O为AD的中点，AB=a．将△ABO沿BO对折于△A′BO，点M为BC上一动点，则A′M的最小值为 ‎ ‎7、在Rt△ACB中，∠ACB=90°，AC=6，BC=8，P、Q两点分别是边AC、BC上的动点，将△PCQ沿PQ翻折，C点的对应点为，连接A，则A的最小值是_________‎ ‎8、如图，在△ABC中，∠ACB=90°，AC=4，BC=2，点A、C分别在x轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动，在运动过程中，点B到原点的最大距离是 .‎ ‎9、如图,△ABC是以AB为斜边的直角三角形,AC=4,BC=3,P为边AB上一动点,且PE⊥AC于点E,PF⊥BC于点F,则线段EF长度的最小值是_____‎ ‎10、如图,正方形ABCD边长为2,当点A在x轴上运动时,点D随之在y轴上运动,在运动过程中,点B到原点O的最大距离为_______‎ ‎11、如图，直角梯形纸片ABCD，AD⊥AB，AB=8，AD=CD=4，点E、F分别在线段AB、AD上，将△AEF沿EF翻折，点A的落点记为P．‎ ‎（1）当P落在线段CD上时，PD的取值范围为 ； （2）当P落在直角梯形ABCD内部时，PD的最小值等于 . ‎ 类型四 圆外点和圆的最值 圆O所在平面上的一点P到圆O上的点的最大距离是10，最小距离是2，求此圆的半径是多少？‎ 综合提升 ‎1、动手操作：在矩形纸片ABCD中，AB=3,AD=5．如图所示，折叠纸片，使点A落在BC边上的A′处，折痕为PQ，当点A′在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点A′在BC边上可移动的最大距离为 ．‎ ‎2、如图，菱形ABCD中，∠A=60°，AB=4，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙A和⊙B上的动点，则PE+PF的最小值是 ．‎ ‎3、在平面直角坐标系中，对于任意两点与的“非常距离”，给出如下定义：‎ 若，则点与点的“非常距离”为；‎ 若，则点与点的“非常距离”为．‎ 例如：点，点，因为，所以点与点的“非常距离”为，也就是图1中线段与线段长度的较大值（点为垂直于轴的直线与垂直于轴的直线的交点）．‎ ‎1）已知点，为轴上的一个动点，‎ ‎①若点与点的“非常距离”为2，写出一个满足条件的点的坐标；‎ ‎②直接写出点与点的“非常距离”的最小值；‎ ‎（2）已知是直线上的一个动点，‎ ‎①如图2，点的坐标是（0，1），求点与点的“非常距离”的最小值及相应的点的坐标；‎ ‎②如图3，是以原点为圆心，1为半径的圆上的一个动点，求点与点的“非常距离”的最小值及相应的点和点的坐标 ‎4、在平面直角坐标系中，已知抛物线（为常数）的顶点为，等腰直角三角形的定点的坐标为，的坐标为，直角顶点在第四象限.‎ ‎（1）如图，若该抛物线过 ，两点，求该抛物线的函数表达式；‎ ‎（2）平移（1）中的抛物线，使顶点在直线上滑动，且与交于另一点.‎ i）若点在直线下方，且为平移前（1）中的抛物线上的点，当以 三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点的坐标；‎ ii）取的中点，连接.试探究是否存在最大值？若存在，求出该最大值；若不存在，请说明理由.‎