2012年沈阳市中考数学仿真模拟及答案（3） 11页

‎2 012年中考仿真模拟（3）‎ ‎ 数 学 试 卷 ‎ ‎1、本卷共8页，总分120分，考试时间120分钟。‎ ‎ ‎ 题号 一 二 三 总分 得分 卷Ⅰ（选择题，共30分）‎ 一、选择题（本大题共12个小题，1—6小题，每小题2分；7—12小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．计算：的结果正确的是………………………………………………【 】‎ A．0 B．‎1 ‎C．2 D．‎ 图1‎ ‎1‎ ‎2‎ ‎2．如图1，把一块含有角的直角三角板的两个顶点放在直尺的对边上．如果，那么的度数是………………【 】‎ A．　　 B．　　 C．　　 D．‎ ‎3．下列计算正确的是……………………………【 】‎ ‎ A. B. ‎ C. D. ‎ ‎4．在平面直角坐标系中，点A（2,3）与点B关于轴对称，则点B的坐标为……【 】‎ A.（3,2） B.（－2，－3） C.（－2,3） D.(2,－3)‎ A B C D 图2‎ ‎5．如图2，这是一个正面为黑、反面为白的未拼完的拼木盘，给出如下四块正面为黑、反面为白的拼木，现欲拼满拼木盘使其颜色一致．那么应该选择的拼木是……【 】‎ ‎ ‎ ‎6．若x，y为实数，且，则的值是……………………【 】‎ A.0 B. －‎1 ‎‎ ‎ C. 1 D.－2012‎ ‎7．石家庄市2011年某一周的最高气温统计如下表：‎ 最高气温（℃）‎ ‎25‎ ‎26‎ ‎27‎ ‎28‎ 天 数 ‎1‎ ‎1‎ ‎2‎ ‎3‎ 则这组数据的中位数与众数分别是………………………………………………【 】‎ A．27，28 B．27.5，‎28 ‎ C．28，27 D．26.5，27‎ ‎8．已知一次函数(为常数)的图象经过点(3,5),则其图象不经过……【 】‎ 图3‎ ‎ A．第一象限　　 B．第二象限　 　C．第三象限　　 D．第四象限 ‎9．两个大小不同的球在水平面上靠在一起，组成如图3‎ 所示的几何体，则该几何体的左视图是……【 】‎ A．两个外离的圆 B．两个外切的圆 ‎ C．两个相交的圆 D．两个内切的圆 ‎10. 如图4所示，已知在三角形纸片ABC中，BC=3， ‎ A B C D E 图4‎ AB=5，∠BCA=90°，在AC上取一点E，以BE为折 痕，使AB的一部分与BC重合，A与BC延长线上的 点D重合，则DE的长度为…………………【 】‎ A． B．‎3 ‎C． D．‎ 图5‎ ‎11. 如图5，已知A、B是反比例函数 (k>0,x>0)图象上的两点，BC∥x轴,交y轴于点C．动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C．过P作PM⊥x轴，PN⊥y轴，垂足分别为M、N．设四边形OMPN的面积为S，P点运动时间为t，则S关于t的函数图象大致为…………………………【 】‎ A ‎ B ‎ C ‎ D ‎ E ‎ F ‎ G ‎ H ‎ 图6‎ ‎12．如图6，在菱形ABCD中，AB=BD，点E，F分 别在AB，AD上，且AE=DF.连接BF与DE相交 于点G，连接CG与BD相交于点H.下列结论：‎ ‎①△AED≌△DFB；②；‎ ‎③若AF=2DF，则BG=6GF.其中正确的结论【 】‎ A.只有①②  B.只有①③ C.只有②③  D.①②③‎ 卷Ⅱ（非选择题，共90分）‎ 二、填空题（本大题共6个小题；每小题3分，共18分．把答案写在题中横线上）‎ ‎13．-2的倒数是_________‎ ‎14．明天数学课要学“勾股定理”，小敏在“百度”搜索引擎中输入“勾股定理”，能搜索到与之相关的结果个数约为12 500 000，这个数用科学记数法表示为_________.‎ ‎15．若，，则的值为 ． ‎ ‎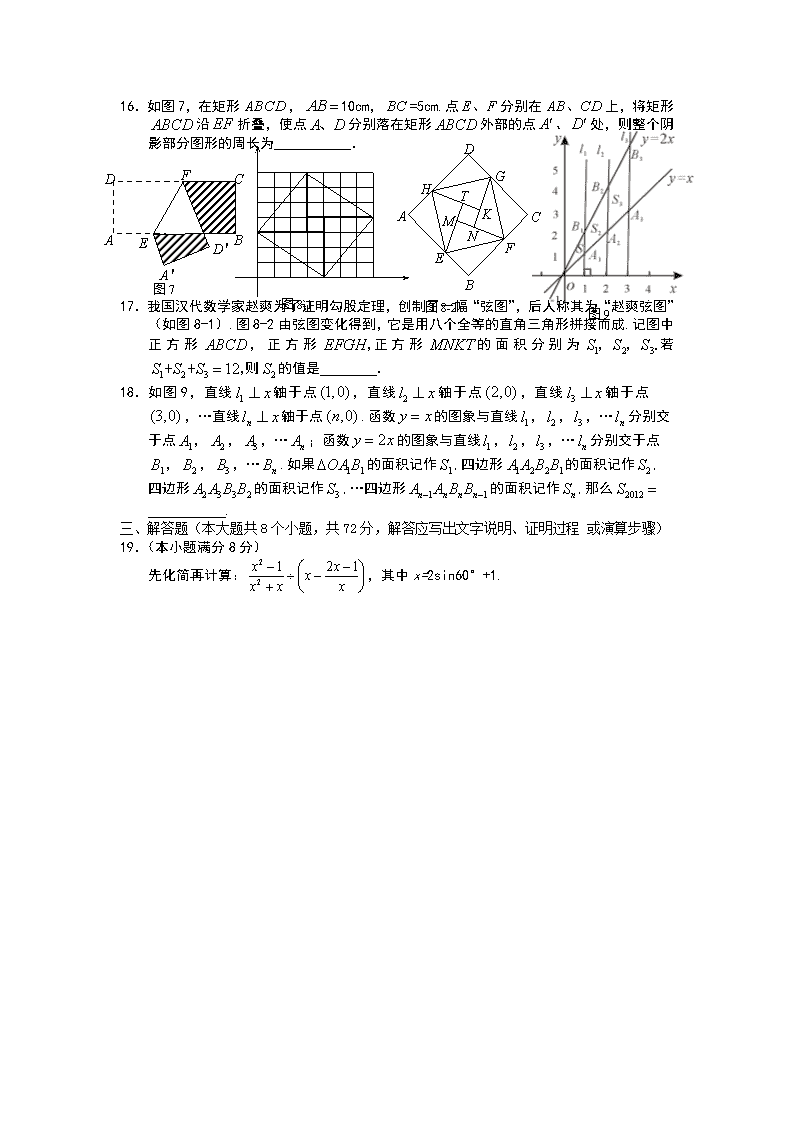16．如图7，在矩形，‎10cm，=‎5cm.点分别在上，将矩形沿折叠，使点分别落在矩形外部的点、处，则整个阴影部分图形的周长为___________．‎ 图9‎ 图8-2‎ D A B C H E M N K T G F 图8-1‎ A D C B E D＇‎ A＇‎ F ‎ 图7‎ ‎17．我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图8-1）.图8-2由弦图变化得到，它是用八个全等的直角三角形拼接而成.记图中正方形，正方形正方形的面积分别为若则的值是　　　　． ‎ ‎18．如图9，直线轴于点，直线轴于点，直线轴于点 ‎，…直线轴于点.函数的图象与直线，，，…分别交于点，，，…；函数的图象与直线，，，…分别交于点，，，….如果的面积记作,四边形的面积记作,四边形的面积记作,…四边形的面积记作,那么 ‎ . ‎ 三、解答题（本大题共8个小题，共72分，解答应写出文字说明、证明过程 或演算步骤）‎ ‎19．（本小题满分8分）‎ 先化简再计算：，其中x=2sin60°+1.‎ ‎20．（本小题满分8分）‎ 图10‎ 如图10，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．‎ ‎（1）请完成如下操作：‎ ‎①以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长，建立平面直角坐标系；②用直尺和圆规画出该圆弧所在圆的圆心D的位置（不用写作法，保留作图痕迹），并连接AD、CD．‎ ‎（2）请在（1）的基础上，完成下列问题：‎ ‎①写出点的坐标：C 、D ；‎ ‎②⊙D的半径= （结果保留根号）；‎ ‎③若扇形ADC是一个圆锥的侧面展开图，则该圆锥的底面面积为 （结果保留π）；‎ ‎④若E（7，0），试判断直线EC与⊙D的位置关系_____________．‎ ‎21．（本小题满分8分）‎ 为了加强食品安全管理，有关部门对石家庄某大型超市的甲、乙两种品牌食用油共抽取18瓶进行检测，检测结果分成“优秀”、“合格”、“不合格”三个等级，数据处理后制成以下折线统计图11-1和扇形统计图11-2．‎ ‎（1）甲、乙两种品牌食用油各被抽取了多少瓶用于检测？‎ ‎（2）在该超市购买一瓶乙品牌食用油，请估计能买到“优秀”等级的概率是多少？‎ 两种品牌食用油检测结果折线图 瓶数 优秀 合格 不合格 ‎7‎ ‎10‎ O ‎1‎ 等级 不合格的10%‎ 合格的30%‎ 优秀60%‎ 甲种品牌食用油检测结果 扇形分布图 图11-1‎ 图11-2‎ ‎22．（本小题满分8分）‎ 石家庄28中九年级（3）班到毕业时共结余班费1800元，班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品，其余资金用于在毕业晚会上给50位同学每人购买一件T恤或一本影集作为纪念品．已知每件T恤比每本影集贵9元，用200元恰好可以买到2件T恤和5本影集．‎ ‎（1）求每件T恤和每本影集的价格分别为多少元？‎ ‎（2）有几种购买T恤和影集的方案？‎ ‎23．（本小题满分9分）‎ ‎（1）正方形ABCD与等腰直角三角形PAQ如图12-1所示重叠在一起，其中∠PAQ=90°，点Q在BC上，连结PD，△ADP与△ABQ全等吗？请说明理由。‎ ‎（2）如图12-2，O为正方形ABCD对角线的交点，将一直角三角板FPQ的直角顶点F与点O重合转动三角板使两直角边始终与BC、AB相交于点M、N，使探索OM与ON的数量关系，并说明理由。‎ ‎（3）如图12-3，将（2）中的“正方形”改成“长方形”，其它的条件不变，且AB=4，AD=6，FM=x，FN=y，试求y与x之间的函数关系式。‎ A A A B B B C C C D D D P P P Q Q Q M M N N O(F)‎ O(F)‎ 图12-1‎ 图12-2‎ 图12-3‎ ‎24．（本小题满分9分）‎ 石家庄市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：．‎ ‎（1）设李明每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？‎ ‎（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？‎ ‎（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？（成本＝进价×销售量）‎ ‎25．（本小题满分10分）‎ 阅读下列材料：‎ 图13-2‎ 图13-1‎ 图13-3‎ 小伟遇到这样一个问题：如图13-1，在梯形中，，对角线、相较于点．若梯形的面积为1，试求以、、的长度为三边长的三角形的面积．‎ 小伟是这样思考的：要想解决这个问题，首先应想办法移动这些分散的线段，构造一个三角形，在计算面积即可．他先后尝试了翻折、旋转、平移的方法后，发现通过平移可以解决这个问题．他的方法是过点作的平行线交的延长线于点，得到的即是以、、的长度为三边长的三角形（如图13-2）．‎ 请你回答：图13-2中的面积等于 ．‎ 参考小伟同学思考问题的方法，解决下列问题：‎ 如图13-3，的三条中线分别为、、．‎ ‎（1）在图13-3中利用图形变换画出并指明以、、的长度为三边长的一个三角形（保留作图痕迹），并说明理由 ‎（2）若的面积为1，则以、、的长度为三边长的三角形的面积等于 ．‎ ‎26．(本小题满分12分)‎ ‎ 如图14，已知抛物线与轴交于A、B两点（A点在B点左侧），与y轴交于点C（0，－3），对称轴是直线x=1，直线BC与抛物线的对称轴交于点D．‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）求直线BC的函数表达式；‎ ‎（3）点E为y轴上一动点，CE的垂直平分线交CE于点F，交抛物线于P、Q两点，且点P在第三象限．①当线段PQ=AB时，求tan∠CED的值；②当以点C、D、E为顶点的三角形是直角三角形时，请直接写出点P的坐标．‎ 温馨提示：可以根据第⑶问的题意，在备图中补出图形，以便作答．‎ B A O C D ‎1‎ ‎1‎ x=1‎ x y 图14-1‎ 备用图 B A O C D ‎1‎ ‎1‎ x=1‎ x y ‎2012年中考仿真模拟（三）‎ 数学试卷参考答案 ‎1-5.DBCDB 6-10.CABDC 11-12.AD ‎ ‎13. 14. 15. 10 16. ‎30cm 17. 4 18. 2011.5 ‎ ‎19.解：‎ ‎=-----------------------------------2分 ‎==---------------------------------------5分 ‎ x=2sin60°+1=--------------------------6分 ‎ 所以原式===. ------------------------------8分 图1‎ ‎20. 解：如图1，（1）①建立平面直角坐标系-----1分 ‎②找出圆心-----------------------------3分 ‎（2）①C（6，2）；D（2，0）--------------5分 ‎②--------------------------------6分 ‎③π---------------------------------7分 ‎④直线EC与⊙D相切---------------------8分 ‎21. 解：21.(1)由不合格瓶数为1知道甲不合格的瓶数为1，‎ ‎%=10瓶，18-10=8瓶，‎ ‎∴甲被抽取了10瓶，乙被抽取了8瓶------------------------------4分 ‎(2)甲种品牌优秀的有1060%=6瓶，10-6=4瓶 ‎∴P（优秀）==，∴估计能买到“优秀”等级的概率是.--------------8分 ‎22. 解：（1）设T恤和影集的价格分别为元和元．则 ‎ ，解得----------------------2分 答：T恤和影集的价格分别为35元和26元．--------------------3分 ‎（2）设购买T恤件，则购买影集 (50-) 本，则 ‎，解得，---------------------6分 ‎∵为正整数，∴= 23，24，25，------------------------------------7分 即有三种方案．第一种方案：购T恤23件，影集27本；‎ 第二种方案：购T恤24件，影集26本；‎ 第三种方案：购T恤25件，影集25本．------------------8分 ‎23. 解：(1) △ADP与△ABQ全等-------------------------------------1分 ‎∵正方形ABCD，∴AB=AD ‎∵等腰直角三角形PAQ，∴AQ=AP----------------------------2分 ‎∵∠PAD+∠QAD =90°∠BAQ+∠QAD =90°‎ ‎∴∠PAD=∠BAQ，∴△ADP≌△ABQ---------------------------3分 ‎（2）OM=ON----------------------------------------------4分 ‎∵正方形ABCD，∴AC⊥BD ‎∵∠AON+∠NOB =90°∠BOM+∠NOB =90°‎ ‎∴∠AON=∠BOM------------------------------------------5分 ‎∵∠OBM=∠OAN=45°OA=OB，∴△AON≌△BOM ‎∴OM=ON------------------------------------------------6分 ‎（3）如图2，过点O作OE⊥AB于E，O H⊥BC于H-------------7分 A B C D P Q M N O(F)‎ H E 图2‎ ‎∴∠OEN=∠OHM =90°‎ ‎∵∠NOE+∠EOM =90°∠MOH+∠EOM =90°‎ ‎∴∠NOE =∠MOH，‎ ‎∴△OEN∽△OHM-----------8分 ‎∴,即，‎ 整理得--------------------9分 ‎24. 解：（1）由题意，得：w = (x－20)·y=(x－20)·(-10x+500)‎ ‎-----------------2分 ‎.‎ 答：当销售单价定为35元时，每月可获得最大利润．------------------3分 ‎（2）由题意，得：-----------------------4分 解这个方程得：x1 = 30，x2 = 40．‎ 答：李明想要每月获得2000元的利润，销售单价应定为30元或40元.-----5分 ‎ ‎（3）∵，∴抛物线开口向下.‎ ‎∴当30≤x≤40时，w≥2000．∵x≤32，∴30≤x≤32时，w≥2000．------6分 ‎∵，，‎ ‎∴y随x的增大而减小.∴当x = 32时，y最小＝180. ------------ ----7分 ‎∵当进价一定时，销售量越小，成本越小，‎ ‎∴（元）-------------------------------------8分 答：想要每月获得的利润不低于2000元，每月的成本最少为3600元．---------- 9分 ‎25. 解：△BDE的面积等于1．------------------------------------------2分 ‎（1）如图3．以AD、BE、CF的长度为三边长的一个三角形是△CFP．-----4分 平移AD至PC，连结AP、FE、FP得AD∥PC且AD =PC ‎∴四边形ADCP是平行四边形，∴AP∥DC且AP =DC ‎∵AF =FB AE =EC，∴EF∥DC EF ==DC ‎∴AP∥EF且AP =EF，∴四边形AFEP是平行四边形 ‎∴AB∥EP且AF =EP，∴BF =EP ‎∴四边形FBEP是平行四边形，∴BE =FP ‎∴以AD、BE、CF的长度为三边长的一个三角形是△CFP．-----------------8分 ‎（2） -----------------------------------10分 ‎26. 解：(1)∵抛物线的对称轴为直线x=1，‎ ‎∴，‎ ‎∴b=－2．‎ ‎∵抛物线与y轴交于点C（0，－3），‎ ‎∴c=－3， ‎ ‎∴抛物线的函数表达式为------------------3分 ‎(2)∵抛物线与x轴交于A、B两点，当y=0时，．‎ ‎∴,-----------------------------------------4分 ‎∵A点在B点左侧，‎ ‎∴A（－1，0），B（3，0）‎ 设过点B（3，0）、C（0，－3）的直线的函数表达式为y=kx＋m，‎ 则，‎ ‎∴ ‎ ‎∴直线BC的函数表达式为y=x－3．-----------------------------6分 ‎(3)①∵AB=4，PQ=AB，‎ ‎∴PQ =3…----------------------------7分 ‎∵PQ⊥y轴，‎ ‎∴PQ∥x轴，则由抛物线的对称性可得点P的横坐标为，‎ B A O C D ‎1‎ ‎1‎ x=1‎ x y E F P Q G 图4‎ ‎∴P（），‎ ‎∴F（0，），‎ ‎∴FC=3－OF=3－=．‎ ‎∵PQ垂直平分CE于点F，‎ ‎∴CE=2FC=-----------8分 ‎∵点D在直线BC上，‎ ‎∴当x=1时，y=－2，则D（1，－2）．‎ 过点D作DG⊥CE于点G，‎ ‎∴DG=1，CG=1，‎ ‎∴GE=CE－CG=－1=．----------------------------------9分 在Rt△EGD中，tan∠CED=．------------------------- 10分 ‎②（1－，－2），（1－，-）---------------------12分