中考数学模拟试卷含解析7 23页

广东省深圳市2016年中考数学模拟试卷 一、选择题 ‎1．﹣2012的相反数是（　　）‎ A．﹣ B． C．﹣2012 D．2012‎ ‎2．由七个大小相同的正方体组成的几何体如图所示，则它的左视图是（　　）‎ A． B． C． D．‎ ‎3． “提高节能，倡导低碳”，‎2012年3月30日“地球一小时”，深圳市民中心附近几座地标性建筑物都相继熄灭．据深圳供电局统计，在短短一小时里，深圳耗电量比上周六同时段相比减少了33900千瓦时，将33900用科学记数法表示为（结果保留2个有效数字）（　　）‎ A．3.3×104 B．3.4×103 C．33×103 D．3.4×104‎ ‎4．（2016•深圳模拟）下列运算正确的是（　　）‎ A．3a3+4a3=7a6 B．3a2﹣4a2=﹣a2‎ C．3a2•4a3=12a3 D．（3a3）2÷4a3=a2‎ ‎5．某商场试销一种新款衬衫，一周内销信情况如表所示：‎ 型号（厘米）‎ ‎38‎ ‎39‎ ‎40‎ ‎41‎ ‎42‎ ‎43‎ 数量（件）‎ ‎25‎ ‎30‎ ‎36‎ ‎50‎ ‎28‎ ‎8‎ 商场经理要了解哪种型号最畅销，则上述数据的统计量中，对商场经理来说最具有意义的是（　　）‎ A．平均数 B．众数 C．中位数 D．方差 ‎6．某种商品的进价为800元，出售时标价为1200元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于5%，则至多可打（　　）‎ A．6折 B．7折 C．8折 D．9折 ‎7．如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（　　）‎ A．30° B．25° C．20° D．15°‎ ‎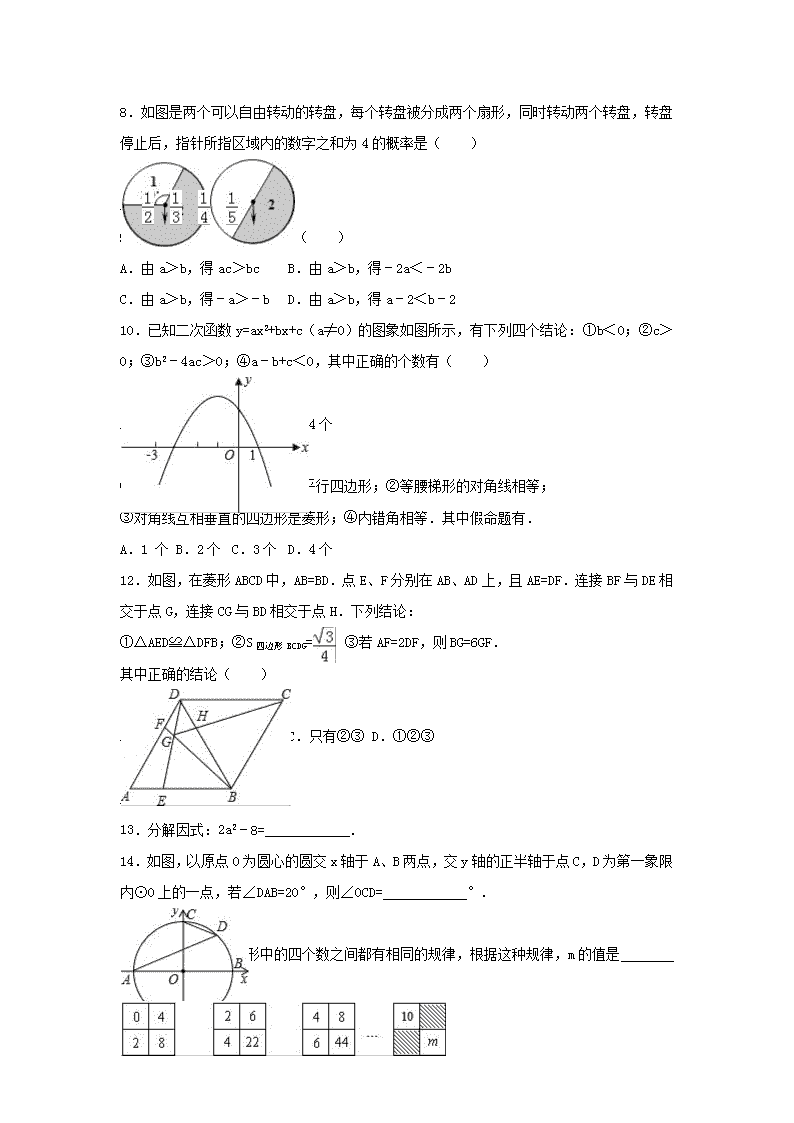8．如图是两个可以自由转动的转盘，每个转盘被分成两个扇形，同时转动两个转盘，转盘停止后，指针所指区域内的数字之和为4的概率是（　　）‎ A． B． C． D．‎ ‎9．下列不等式变形正确的是（　　）‎ A．由a＞b，得ac＞bc B．由a＞b，得﹣2a＜﹣2b C．由a＞b，得﹣a＞﹣b D．由a＞b，得a﹣2＜b﹣2‎ ‎10．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列四个结论：①b＜0；②c＞0；③b2﹣4ac＞0；④a﹣b+c＜0，其中正确的个数有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎11．已知下列命题：（　　）‎ ‎①对角线互相平分的四边形是平行四边形；②等腰梯形的对角线相等；‎ ‎③对角线互相垂直的四边形是菱形；④内错角相等．其中假命题有．‎ A．1 个 B．2个 C．3个 D．4个 ‎12．如图，在菱形ABCD中，AB=BD．点E、F分别在AB、AD上，且AE=DF．连接BF与DE相交于点G，连接CG与BD相交于点H．下列结论：‎ ‎①△AED≌△DFB；②S四边形BCDG=CG2；③若AF=2DF，则BG=6GF．‎ 其中正确的结论（　　）‎ A．只有①② B．只有①③ C．只有②③ D．①②③‎ ‎　‎ 二、填空题：‎ ‎13．分解因式：2a2﹣8=　　　　　　．‎ ‎14．如图，以原点O为圆心的圆交x轴于A、B两点，交y轴的正半轴于点C，D为第一象限内⊙O上的一点，若∠DAB=20°，则∠OCD=　　　　　　°．‎ ‎15．填在如图各正方形中的四个数之间都有相同的规律，根据这种规律，m的值是　　　　　　．‎ ‎16．如图，在平面直角坐标系中有一正方形AOBC，反比例函数经过正方形AOBC对角线的交点，半径为（4﹣2）的圆内切于△ABC，则k的值为　　　　　　．‎ ‎　‎ 三、解答题 ‎17．计算：．‎ ‎18．解方程：‎ ‎19．某中学为了解学生的课外阅读情况，就“我最喜爱的课外读物”从文学、艺术、科普和其它四个类别进行了抽样调查（每位同学仅选一项），并根据调查结果制作了尚不完整的频数分布表：‎ 类别 频数（人数）‎ 频率 文学 m ‎0.42‎ 艺术 ‎22‎ ‎0.11‎ 科普 ‎66‎ n 其他 ‎28‎ 合计 ‎1‎ ‎（1）表中m=　　　　　　，n=　　　　　　；‎ ‎（2）在这次抽样调查中，最喜爱阅读哪类读物的学生最少？‎ ‎（4）根据以上调查，试估计该校1200名学生中最喜爱阅读科普读物的学生有多少人？‎ ‎20．如图，在以O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于点A，与大圆相交于点B．小圆的切线AC与大圆相交于点D，且CO平分∠ACB．‎ ‎（1）试判断BC所在直线与小圆的位置关系，并说明理由；‎ ‎（2）试判断线段AC、AD、BC之间的数量关系，并说明理由．‎ ‎（3）若AB=8，BC=10，求大圆与小圆围成的圆环的面积．‎ ‎21．如图，在梯形ABCD中，已知AD∥BC，∠B=90°，AB=7，AD=9，BC=12，在线段BC上任取一点E，连接DE，作EF⊥DE，交直线AB于点F．‎ ‎（1）若点F与B重合，求CE的长；‎ ‎（2）若点F在线段AB上，且AF=CE，求CE的长．‎ ‎22．一家蔬菜公司收购到某种绿色蔬菜140吨，准备加工后进行销售，销售后获利情况如表所示：‎ 销售方式 粗加工后销售 精加工后销售 每吨获利（元）‎ ‎1000‎ ‎2000‎ 已知该公司的加工能力是：每天能精加工5吨或粗加工15吨，但两种加工不能同时进行．受季节等条件的限制，公司必须在一定时间内将这批蔬菜全部加工后销售完．‎ ‎（1）如果要求12天刚好加工完140吨蔬菜，则公司应安排几天精加工，几天粗加工？‎ ‎（2）如果先进行精加工，然后进行粗加工．‎ ‎①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式；‎ ‎②若要求在不超过10天的时间内，将140吨蔬菜全部加工完后进行销售，则加工这批蔬菜最多获得多少利润？此时如何分配加工时间？‎ ‎23．如图，已知知抛物线y=x2+bx+c与x轴交于点A（1，0）和点B，与y轴交于点C（0，﹣3）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）如图（1），己知点H（0，﹣1）．问在抛物线上是否存在点G （点G在y轴的左侧），使得S△GHC=S△GHA？若存在，求出点G的坐标；若不存在，请说明理由；‎ ‎（3）如图（2），抛物线上点D在x轴上的正投影为点E（﹣2，0），F是OC的中点，连接DF，P为线段BD上的一点，若∠EPF=∠BDF，求线段PE的长．‎ ‎　‎ ‎2016年广东省深圳市中考数学模拟试卷 参考答案与试题解析 ‎　‎ 一、选择题 ‎1．﹣2012的相反数是（　　）‎ A．﹣ B． C．﹣2012 D．2012‎ ‎【考点】相反数．‎ ‎【分析】根据相反数的定义，只有符号不同的两个数叫做互为相反数解答．‎ ‎【解答】解：﹣2012的相反数是2012．‎ 故选D．‎ ‎【点评】本题考查了相反数的定义，根据相反数的定义：a的相反数是﹣a即可得出正确答案，是基础题，比较简单．‎ ‎　‎ ‎2．由七个大小相同的正方体组成的几何体如图所示，则它的左视图是（　　）‎ A． B． C． D．‎ ‎【考点】简单组合体的三视图．‎ ‎【分析】找到从左面看所得到的图形即可．‎ ‎【解答】解：从左面看可得到第一列为3个正方形，第二列有一个正方形．‎ 故选D．‎ ‎【点评】本题考查了三视图的知识，左视图是从物体的左面看得到的视图．‎ ‎　‎ ‎3． “提高节能，倡导低碳”，‎2012年3月30日“地球一小时”，深圳市民中心附近几座地标性建筑物都相继熄灭．据深圳供电局统计，在短短一小时里，深圳耗电量比上周六同时段相比减少了33900千瓦时，将33900用科学记数法表示为（结果保留2个有效数字）（　　）‎ A．3.3×104 B．3.4×103 C．33×103 D．3.4×104‎ ‎【考点】科学记数法与有效数字．‎ ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值是易错点，由于33900有5位，所以可以确定n=5﹣1=4．‎ 有效数字的计算方法是：从左边第一个不是0的数字起，后面所有的数字都是有效数字．‎ 用科学记数法表示的数的有效数字只与前面的a有关，与10的多少次方无关．‎ ‎【解答】解：33900=3.39×104≈3.4×104．‎ 故选D．‎ ‎【点评】此题考查科学记数法的表示方法，以及用科学记数法表示的数的有效数字的确定方法．‎ ‎　‎ ‎4．下列运算正确的是（　　）‎ A．3a3+4a3=7a6 B．3a2﹣4a2=﹣a2‎ C．3a2•4a3=12a3 D．（3a3）2÷4a3=a2‎ ‎【考点】整式的混合运算．‎ ‎【分析】A、原式合并同类项得到结果，即可作出判断；‎ B、原式合并同类项得到结果，即可作出判断；‎ C、原式利用单项式乘以单项式法则计算得到结果，即可作出判断；‎ D、原式先计算乘方运算，再计算除法运算得到结果，即可作出判断．‎ ‎【解答】解：A、原式=7a3，错误；‎ B、原式=﹣a2，正确；‎ C、原式=12a5，错误；‎ D、原式=9a6÷4a3=a3，错误，‎ 故选B ‎【点评】此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．‎ ‎　‎ ‎5．某商场试销一种新款衬衫，一周内销信情况如表所示：‎ 型号（厘米）‎ ‎38‎ ‎39‎ ‎40‎ ‎41‎ ‎42‎ ‎43‎ 数量（件）‎ ‎25‎ ‎30‎ ‎36‎ ‎50‎ ‎28‎ ‎8‎ 商场经理要了解哪种型号最畅销，则上述数据的统计量中，对商场经理来说最具有意义的是（　　）‎ A．平均数 B．众数 C．中位数 D．方差 ‎【考点】统计量的选择．‎ ‎【分析】根据题意可知最畅销的应为众数，本题得以解决．‎ ‎【解答】解：由题意可知，‎ 最畅销的型号应该是销售量最多的型号，‎ 故对商场经理来说最具有意义的是众数，‎ 故选B．‎ ‎【点评】本题考查统计量的选择，解题的关键是明确题意，找出满足所求问题的条件．‎ ‎　‎ ‎6．某种商品的进价为800元，出售时标价为1200元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于5%，则至多可打（　　）‎ A．6折 B．7折 C．8折 D．9折 ‎【考点】一元一次不等式的应用．‎ ‎【分析】本题可设打x折，根据保持利润率不低于5%，可列出不等式：1200×﹣800≥800×5%，解出x的值即可得出打的折数．‎ ‎【解答】解：设可打x折，则有1200×﹣800≥800×5%，‎ 解得x≥7．‎ 即最多打7折．‎ 故选：B．‎ ‎【点评】本题考查的是一元一次不等式的应用，解此类题目时注意利润和折数，计算折数时注意要除以10．‎ ‎　‎ ‎7．如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（　　）‎ A．30° B．25° C．20° D．15°‎ ‎【考点】平行线的性质．‎ ‎【分析】本题主要利用两直线平行，内错角相等作答．‎ ‎【解答】解：根据题意可知，两直线平行，内错角相等，‎ ‎∴∠1=∠3，‎ ‎∵∠3+∠2=45°，‎ ‎∴∠1+∠2=45°‎ ‎∵∠1=20°，‎ ‎∴∠2=25°．‎ 故选：B．‎ ‎【点评】本题主要考查了两直线平行，内错角相等的性质，需要注意隐含条件，直尺的对边平行，等腰直角三角板的锐角是45°的利用．‎ ‎　‎ ‎8．如图是两个可以自由转动的转盘，每个转盘被分成两个扇形，同时转动两个转盘，转盘停止后，指针所指区域内的数字之和为4的概率是（　　）‎ A． B． C． D．‎ ‎【考点】几何概率．‎ ‎【分析】根据几何概率的定义，分别求出两圆中2所占的面积，即可求出针头扎在阴影区域内的概率．‎ ‎【解答】解：指针指向（1）中2的概率是，指针指向（2）中2的概率是，‎ 指针所指区域内的数字之和为4的概率是×=．‎ 故选B．‎ ‎【点评】此题考查学生对简单几何概型的掌握情况，既避免了单纯依靠公式机械计算的做法，又体现了数学知识在现实生活、甚至娱乐中的运用，体现了数学学科的基础性．两步完成的事件的概率=第一步事件的概率与第二步事件的概率的积．‎ ‎　‎ ‎9．下列不等式变形正确的是（　　）‎ A．由a＞b，得ac＞bc B．由a＞b，得﹣2a＜﹣2b C．由a＞b，得﹣a＞﹣b D．由a＞b，得a﹣2＜b﹣2‎ ‎【考点】不等式的性质．‎ ‎【分析】根据不等式的基本性质分别进行判定即可得出答案．‎ ‎【解答】解：A．由a＞b，得ac＞bc，当c＜0，不等号的方向改变．故A选项错误；‎ B．由a＞b，得﹣2a＜﹣2b，不等式两边乘以同一个负数，不等号的方向改变，故B选项正确；‎ C．由a＞b，得﹣a＞﹣b，不等式两边乘（或除以）同一个负数，不等号的方向改变；故C选项错误；‎ D．由a＞b，得a﹣2＜b﹣2，不等式两边同时减去一个数，不等号方向不改变，故D选项错误．‎ 故选B．‎ ‎【点评】此题主要考查了不等式的基本性质．“0”是很特殊的一个数，因此，解答不等式的问题时，应密切关注“0”存在与否，以防掉进“0”的陷阱．不等式的基本性质：‎ ‎（1）不等式两边加（或减）同一个数（或式子），不等号的方向不变．‎ ‎（2）不等式两边乘（或除以）同一个正数，不等号的方向不变．‎ ‎（3）不等式两边乘（或除以）同一个负数，不等号的方向改变．‎ ‎　‎ ‎10．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列四个结论：①b＜0；②c＞0；③b2﹣4ac＞0；④a﹣b+c＜0，其中正确的个数有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎【考点】二次函数图象与系数的关系．‎ ‎【分析】由抛物线开口向下知道a＜0，而对称轴在y轴左侧，即b＜0，因此判断①正确；‎ 由抛物线与y轴的交点在正半轴得到c＞0，因此可以判断②正确；‎ 由图象与x轴有两个交点得到以b2﹣4ac＞0，因此可以判断③正确；‎ 由图象可知当x=﹣1时，对应的函数值y=a﹣b+c＞0，所以判断④错．‎ ‎【解答】解：①∵抛物线开口向下，∴a＜0，而对称轴在y轴左侧，∴a、b同号，即b＜0，正确；‎ ‎②∵抛物线与y轴的交点在正半轴，∴c＞0，正确；‎ ‎③∵图象与x轴有两个交点，∴b2﹣4ac＞0，正确；‎ ‎④∵由图象可知当x=﹣1时，对应的函数值y=a﹣b+c＞0，错误．‎ 故选C．‎ ‎【点评】本题考查二次函数的字母系数与图象位置之间的关系．‎ ‎　‎ ‎11．已知下列命题：（　　）‎ ‎①对角线互相平分的四边形是平行四边形；②等腰梯形的对角线相等；‎ ‎③对角线互相垂直的四边形是菱形；④内错角相等．其中假命题有．‎ A．1 个 B．2个 C．3个 D．4个 ‎【考点】命题与定理．‎ ‎【分析】利用平行四边形的判定、菱形的判定、等腰梯形的性质及平行线的性质分别判断后即可确定正确的选项．‎ ‎【解答】解：①对角线互相平分的四边形是平行四边形，正确，是真命题；‎ ‎②等腰梯形的对角线相等，正确，是真命题；‎ ‎③对角线互相垂直的平行四边形是菱形，错误，为假命题；‎ ‎④两直线平行，内错角相等故错误，是假命题．‎ 其中假命题有2个，‎ 故选B．‎ ‎【点评】本题考查了命题与定理的知识，解题的关键是了解平行四边形的判定、菱形的判定、等腰梯形的性质及平行线的性质，难度不大．‎ ‎　‎ ‎12．如图，在菱形ABCD中，AB=BD．点E、F分别在AB、AD上，且AE=DF．连接BF与DE相交于点G，连接CG与BD相交于点H．下列结论：‎ ‎①△AED≌△DFB；②S四边形BCDG=CG2；③若AF=2DF，则BG=6GF．‎ 其中正确的结论（　　）‎ A．只有①② B．只有①③ C．只有②③ D．①②③‎ ‎【考点】旋转的性质；全等三角形的判定与性质；等边三角形的判定与性质；平行线分线段成比例．‎ ‎【分析】①易证△ABD为等边三角形，根据“SAS”证明△AED≌△DFB；‎ ‎②证明∠BGE=60°=∠BCD，从而得点B、C、D、G四点共圆，因此∠BGC=∠DGC=60°．过点C作CM⊥GB于M，CN⊥GD于N．证明△CBM≌△CDN，所以S四边形BCDG=S四边形CMGN，易求后者的面积．‎ ‎③过点F作FP∥AE于P点．‎ 根据题意有FP：AE=DF：DA=1：3，则FP：BE=1：6=FG：BG，即BG=6GF．‎ ‎【解答】解：①∵ABCD为菱形，∴AB=AD．‎ ‎∵AB=BD，∴△ABD为等边三角形．‎ ‎∴∠A=∠BDF=60°．‎ 又∵AE=DF，AD=BD，‎ ‎∴△AED≌△DFB；‎ ‎②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD，‎ 即∠BGD+∠BCD=180°，‎ ‎∴点B、C、D、G四点共圆，‎ ‎∴∠BGC=∠BDC=60°，∠DGC=∠DBC=60°．‎ ‎∴∠BGC=∠DGC=60°．‎ 过点C作CM⊥GB于M，CN⊥GD于N．‎ ‎∴CM=CN，‎ ‎∵，‎ ‎∴△CBM≌△CDN，（HL）‎ ‎∴S四边形BCDG=S四边形CMGN．‎ S四边形CMGN=2S△CMG，‎ ‎∵∠CGM=60°，‎ ‎∴GM=CG，CM=CG，‎ ‎∴S四边形CMGN=2S△CMG=2××CG×CG=CG2．‎ ‎③过点F作FP∥AE于P点．‎ ‎∵AF=2FD，‎ ‎∴FP：AE=DF：DA=1：3，‎ ‎∵AE=DF，AB=AD，‎ ‎∴BE=2AE，‎ ‎∴FP：BE=1：6=FG：BG，‎ 即 BG=6GF．‎ 故选D．‎ ‎【点评】此题综合考查了全等三角形的判定和性质、平行线分线段成比例、不规则图形的面积计算方法等知识点，综合性较强，难度较大．‎ ‎　‎ 二、填空题：‎ ‎13．分解因式：2a2﹣8=　2（a+2）（a﹣2）　．‎ ‎【考点】提公因式法与公式法的综合运用．‎ ‎【分析】先提取公因式2，再对余下的多项式利用平方差公式继续分解．‎ ‎【解答】解：2a2﹣8‎ ‎=2（a2﹣4），‎ ‎=2（a+2）（a﹣2）．‎ 故答案为：2（a+2）（a﹣2）．‎ ‎【点评】本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．‎ ‎　‎ ‎14．如图，以原点O为圆心的圆交x轴于A、B两点，交y轴的正半轴于点C，D为第一象限内⊙O上的一点，若∠DAB=20°，则∠OCD=　65　°．‎ ‎【考点】圆周角定理；坐标与图形性质．‎ ‎【分析】根据∠DAB=20°，得出∠DOB的度数，再利用等腰三角形的性质得出∠OCD=∠CDO，进而求出答案．‎ ‎【解答】解：连接DO，∵∠DAB=20°，‎ ‎∴∠DOB=40°，‎ ‎∴∠COD=90°﹣40°=50°，‎ ‎∵CO=DO，‎ ‎∴∠OCD=∠CDO，‎ ‎∴∠OCD=（180°﹣50°）÷2=65°．‎ 故答案为：65．‎ ‎【点评】此题主要考查了圆周角定理以及等腰三角形的性质，得出∠OCD=∠CDO是解决问题的关键．‎ ‎　‎ ‎15．填在如图各正方形中的四个数之间都有相同的规律，根据这种规律，m的值是　158　．‎ ‎【考点】规律型：数字的变化类．‎ ‎【分析】设第n个正方形中的四个数（从左上角开始按逆时针排列）为an、bn、cn、dn，根据给定的数据找出cn的变化规律“cn=4n2+2n+2”，依此规律即可解决问题．‎ ‎【解答】解：设第n个正方形中的四个数（从左上角开始按逆时针排列）为an、bn、cn、dn，‎ 观察，发现规律：‎ ‎∵a1=0，a2=2，a3=4，…，‎ ‎∴an=2（n﹣1）；‎ ‎∵b1=2，b2=4，b3=6，…，‎ ‎∴bn=2n；‎ ‎∵d1=4，d2=6，d3=8，…，‎ ‎∴dn=2（n+1）；‎ ‎∵c1=8═2×4﹣0=b1•d1﹣a1，c2=22=4×6﹣2=b2•d2﹣c2，c3=44=6×8﹣4=b3•d3﹣a3，…，‎ ‎∴cn=bn•dn﹣an=4n2+2n+2．‎ 令an=2（n﹣1）=10，解得：n=6．‎ ‎∴c6=4×62+2×6+2=158．‎ 故答案为：158．‎ ‎【点评】本题考查了规律型中的数字的变化类，解题的关键是求出正方形中右下角数的变化的规律“cn=4n2+2n+2”．本题属于中档题，难度不大，解题的关键是根据给定的数据，找出变化规律是关键．‎ ‎　‎ ‎16．如图，在平面直角坐标系中有一正方形AOBC，反比例函数经过正方形AOBC对角线的交点，半径为（4﹣2）的圆内切于△ABC，则k的值为　4　．‎ ‎【考点】三角形的内切圆与内心；待定系数法求反比例函数解析式；正方形的性质．‎ ‎【分析】根据正方形的性质得出AD=BD=DO=CD，NO=DN，HQ=QE，HC=CE，进而根据半径为（4﹣2）的圆内切于△ABC，得出CD的长，从而得出DO的长，再利用勾股定理得出DN的长进而得出k的值．‎ ‎【解答】解：设正方形对角线交点为D，过点D作DM⊥AO于点M，DN⊥BO于点N；‎ 设圆心为Q，切点为H、E，连接QH、QE．‎ ‎∵在正方形AOBC中，反比例函数经过正方形AOBC对角线的交点，‎ ‎∴AD=BD=DO=CD，NO=DN，HQ=QE，HC=CE，‎ QH⊥AC，QE⊥BC，∠ACB=90°，‎ ‎∴四边形HQEC是正方形，‎ ‎∵半径为（4﹣2）的圆内切于△ABC，‎ ‎∴DO=CD，‎ ‎∵HQ2+HC2=QC2，‎ ‎∴2HQ2=QC2=2×（4﹣2）2，‎ ‎∴QC2=48﹣32=（4﹣4）2，‎ ‎∴QC=4﹣4，‎ ‎∴CD=4﹣4+（4﹣2）=2，‎ ‎∴DO=2，‎ ‎∵NO2+DN2=DO2=（2）2=8，‎ ‎∴2NO2=8，‎ ‎∴NO2=4，‎ ‎∴DN×NO=4，‎ 即：xy=k=4．‎ 故答案为：4．‎ ‎【点评】此题主要考查了正方形的性质以及三角形内切圆的性质以及待定系数法求反比例函数解析式，根据已知求出CD的长度，进而得出DN×NO=4是解决问题的关键．‎ ‎　‎ 三、解答题 ‎17．计算：．‎ ‎【考点】实数的运算；零指数幂；负整数指数幂；特殊角的三角函数值．‎ ‎【分析】本题需先根据实数运算的步骤和法则分别进行计算，再把所得结果合并即可．‎ ‎【解答】解：原式=，‎ ‎=．‎ ‎【点评】本题主要考查了实数的运算，在解题时要注意运算顺序和公式的综合应用以及结果的符号是本题的关键．‎ ‎　‎ ‎18．解方程：‎ ‎【考点】解分式方程．‎ ‎【分析】观察方程可得最简公分母是：（x﹣2）（x+2），两边同时乘最简公分母可把分式方程化为整式方程来解答．‎ ‎【解答】解：方程两边同乘以（x﹣2）（x+2），‎ 得（x﹣2）2+4=（x﹣2）（x+2），‎ 解得x=3．‎ 经检验：x=3是原方程的解．‎ ‎【点评】（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．‎ ‎（2）解分式方程一定注意要验根．‎ ‎　‎ ‎19．某中学为了解学生的课外阅读情况，就“我最喜爱的课外读物”从文学、艺术、科普和其它四个类别进行了抽样调查（每位同学仅选一项），并根据调查结果制作了尚不完整的频数分布表：‎ 类别 频数（人数）‎ 频率 文学 m ‎0.42‎ 艺术 ‎22‎ ‎0.11‎ 科普 ‎66‎ n 其他 ‎28‎ 合计 ‎1‎ ‎（1）表中m=　84　，n=　0.33　；‎ ‎（2）在这次抽样调查中，最喜爱阅读哪类读物的学生最少？‎ ‎（4）根据以上调查，试估计该校1200名学生中最喜爱阅读科普读物的学生有多少人？‎ ‎【考点】频数（率）分布表；用样本估计总体．‎ ‎【分析】（1）首先求出总人数，利用艺术类的频数与频率进而求出答案；‎ ‎（2）利用（1）中所求，即可得出答案；‎ ‎（3）利用（1）中所求，利用总数乘以0.33即可得出答案．‎ ‎【解答】解：（1）由题意可得：22÷0.11=200，‎ 则m=200×0.42=84，‎ n==0.33，‎ 故答案为：84，0.33；‎ ‎（2）由题意可得：最喜爱阅读艺术类读物的学生最少；‎ ‎（3）1200名学生中最喜爱阅读科普读物的学生有：1200×0.33=396（人）．‎ ‎【点评】此题主要考查了频数与频率，正确得出m，n的值是解题关键．‎ ‎　‎ ‎20．如图，在以O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于点A，与大圆相交于点B．小圆的切线AC与大圆相交于点D，且CO平分∠ACB．‎ ‎（1）试判断BC所在直线与小圆的位置关系，并说明理由；‎ ‎（2）试判断线段AC、AD、BC之间的数量关系，并说明理由．‎ ‎（3）若AB=8，BC=10，求大圆与小圆围成的圆环的面积．‎ ‎【考点】直线与圆的位置关系；扇形面积的计算．‎ ‎【分析】（1）只要证明OE垂直BC即可得出BC是小圆的切线，即与小圆的关系是相切．‎ ‎（2）利用全等三角形的判定得出Rt△OAD≌Rt△OEB，从而得出EB=AD，从而得到三者的关系是前两者的和等于第三者．‎ ‎（3）根据大圆的面积减去小圆的面积即可得到圆环的面积．‎ ‎【解答】解：（1）BC所在直线与小圆相切．‎ 理由如下：‎ 过圆心O作OE⊥BC，垂足为E；‎ ‎∵AC是小圆的切线，AB经过圆心O，‎ ‎∴OA⊥AC；‎ 又∵CO平分∠ACB，OE⊥BC，‎ ‎∴OE=OA，‎ ‎∴BC所在直线是小圆的切线．‎ ‎（2）AC+AD=BC．‎ 理由如下：‎ 连接OD．‎ ‎∵AC切小圆O于点A，BC切小圆O于点E，‎ ‎∴CE=CA；‎ ‎∵在Rt△OAD与Rt△OEB中，‎ ‎，‎ ‎∴Rt△OAD≌Rt△OEB（HL），‎ ‎∴EB=AD；‎ ‎∵BC=CE+EB，‎ ‎∴BC=AC+AD．‎ ‎（3）∵∠BAC=90°，AB=8cm，BC=10cm，‎ ‎∴AC=6cm；‎ ‎∵BC=AC+AD，‎ ‎∴AD=BC﹣AC=4cm，‎ ‎∵圆环的面积为：S=π（OD）2﹣π（OA）2=π（OD2﹣OA2），‎ 又∵OD2﹣OA2=AD2，‎ ‎∴S=42π=16π（cm2）．‎ ‎【点评】本题考查了切线的判定，全等三角形的判定等知识点．要证某线是圆的切线，①已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可，②所证切线与圆的交点不明确，可以过圆心作该直线的垂线段，证明垂线段的长等于半径．‎ ‎　‎ ‎21．如图，在梯形ABCD中，已知AD∥BC，∠B=90°，AB=7，AD=9，BC=12，在线段BC上任取一点E，连接DE，作EF⊥DE，交直线AB于点F．‎ ‎（1）若点F与B重合，求CE的长；‎ ‎（2）若点F在线段AB上，且AF=CE，求CE的长．‎ ‎【考点】相似三角形的判定与性质；矩形的判定与性质；梯形．‎ ‎【分析】（1）根据题意画出图形，得出矩形ABEC求出BE，即可求出CE；‎ ‎（2）过D作DM⊥BC于M，得出四边形ABMD是矩形，推出AD=BM=9，AB=DM=7，CM=12﹣9=3，设AF=CE=a，则BF=7﹣a，EM=a﹣3，BE=12﹣a，求出∠BFE=∠DEM，∠B=∠DME，证△FBE∽△EMD，得出比例式=，求出a即可．‎ ‎【解答】解：（1）当F和B重合时，‎ ‎∵EF⊥DE，‎ ‎∵DE⊥BC，‎ ‎∵∠B=90°，‎ ‎∴AB⊥BC，‎ ‎∴AB∥DE，‎ ‎∵AD∥BC，‎ ‎∴四边形ABED是平行四边形，‎ ‎∴AD=EF=9，‎ ‎∴CE=BC﹣EF=12﹣9=3；‎ ‎（2）过D作DM⊥BC于M，‎ ‎∵∠B=90°，‎ ‎∴AB⊥BC，‎ ‎∴DM∥AB，‎ ‎∵AD∥BC，‎ ‎∴四边形ABMD是矩形，‎ ‎∴AD=BM=9，AB=DM=7，CM=12﹣9=3，‎ 设AF=CE=a，则BF=7﹣a，EM=a﹣3，BE=12﹣a，‎ ‎∵∠FEC=∠B=∠DMB=90°，‎ ‎∴∠FEB+∠DEM=90°，∠BFE+∠FEB=90°，‎ ‎∴∠BFE=∠DEM，‎ ‎∵∠B=∠DME，‎ ‎∴△FBE∽△EMD，‎ ‎∴=，‎ ‎∴=，‎ a=5，a=17，‎ ‎∵点F在线段AB上，AB=7，‎ ‎∴AF=CE=17（舍去），‎ 即CE=5．‎ ‎【点评】本题考查了直角梯形性质，矩形的性质和判定，相似三角形的性质和判定等知识点，主要考查学生综合运用性质进行推理和计算的能力，题目比较典型，是一道比较好的题目．‎ ‎　‎ ‎22．一家蔬菜公司收购到某种绿色蔬菜140吨，准备加工后进行销售，销售后获利情况如表所示：‎ 销售方式 粗加工后销售 精加工后销售 每吨获利（元）‎ ‎1000‎ ‎2000‎ 已知该公司的加工能力是：每天能精加工5吨或粗加工15吨，但两种加工不能同时进行．受季节等条件的限制，公司必须在一定时间内将这批蔬菜全部加工后销售完．‎ ‎（1）如果要求12天刚好加工完140吨蔬菜，则公司应安排几天精加工，几天粗加工？‎ ‎（2）如果先进行精加工，然后进行粗加工．‎ ‎①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式；‎ ‎②若要求在不超过10天的时间内，将140吨蔬菜全部加工完后进行销售，则加工这批蔬菜最多获得多少利润？此时如何分配加工时间？‎ ‎【考点】一次函数的应用．‎ ‎【分析】（1）本题等量关系为：精加工天数+粗加工天数=12，精加工吨数+粗加工吨数=140，列出方程组求解即可．‎ ‎（2）①根据精加工吨数和粗加工吨数的等量关系，用精加工吨数m来表示粗加工吨数，在列出W与m之间的关系，‎ ‎②根据题意要求先确定m的取值范围，然后表示W并求出W最大值．‎ ‎【解答】解：（1）设应安排x天进行精加工，y天进行粗加工，‎ 根据题意得，‎ 解得，‎ 答：应安排4天进行精加工，8天进行粗加工．‎ ‎（2）①精加工m吨，则粗加工（140﹣m）吨，根据题意得：‎ W=2000m+1000（140﹣m）‎ ‎=1000m+140000；‎ ‎②∵要求在不超过10天的时间内将所有蔬菜加工完，‎ ‎∴+≤10，‎ 解得：m≤5‎ ‎∴0≤m≤5，‎ 又∵在一次函数W=1000m+140000中，k=1000＞0，‎ ‎∴W随m的增大而增大，‎ ‎∴当m=5时，W最大=1000×5+140000=145000．‎ ‎∴精加工天数为5÷5=1，‎ 粗加工天数为（140﹣5）÷15=9．‎ ‎∴安排1天进行精加工，9天进行粗加工，可以获得最多利润为145000元．‎ ‎【点评】本题考查了二元一次方程组的应用以及一元一次不等式的应用和一次函数的应用，解题关键在于看清题意，找到正确的等量关系，列出方程式，最后解出答案．‎ ‎　‎ ‎23．如图，已知知抛物线y=x2+bx+c与x轴交于点A（1，0）和点B，与y轴交于点C（0，﹣3）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）如图（1），己知点H（0，﹣1）．问在抛物线上是否存在点G （点G在y轴的左侧），使得S△GHC=S△GHA？若存在，求出点G的坐标；若不存在，请说明理由；‎ ‎（3）如图（2），抛物线上点D在x轴上的正投影为点E（﹣2，0），F是OC的中点，连接DF，P为线段BD上的一点，若∠EPF=∠BDF，求线段PE的长．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）由抛物线y=x2+bx+c与x轴交于点A（1，0）和点B，与y轴交于点C（0，﹣3），利用待定系数法即可求得二次函数的解析式；‎ ‎（2）分别从GH∥AC与GH与AC不平行去分析，注意先求得直线GH的解析式，根据交点问题即可求得答案，小心不要漏解；‎ ‎（3）利用待定系数法求得直线DF的解析式，即可证得△PBE∽△FDP，由相似三角形的对应边成比例，即可求得答案．‎ ‎【解答】解：（1）由题意得：，‎ 解得：，‎ ‎∴抛物线的解析式为：y=x2+2x﹣3；‎ ‎（2）解法一：‎ 假设在抛物线上存在点G，设G（m，n），显然，当n=﹣3时，△HGC不存在．‎ ‎①当n＞﹣3时，‎ 可得S△GHA=﹣++，S△GHC=﹣m，‎ ‎∵S△GHC=S△GHA，‎ ‎∴m+n+1=0，‎ 由，‎ 解得：或，‎ ‎∵点G在y轴的左侧，‎ ‎∴G（﹣，）；‎ ‎②当﹣4≤n＜﹣3时，‎ 可得S△GHA=﹣﹣，S△GHC=﹣m，‎ ‎∵S△GHC=S△GHA，‎ ‎∴3m﹣n﹣1=0，‎ 由，‎ 解得：或，‎ ‎∵点G在y轴的左侧，‎ ‎∴G（﹣1，﹣4）．‎ ‎∴存在点G（﹣，）或G（﹣1，﹣4）．‎ 解法二：‎ ‎①如图①，当GH∥AC时，点A，点C到GH的距离相等，‎ ‎∴S△GHC=S△GHA，‎ 可得AC的解析式为y=3x﹣3，‎ ‎∵GH∥AC，得GH的解析式为y=3x﹣1，‎ ‎∴G（﹣1，﹣4）；‎ ‎②如图②，当GH与AC不平行时，‎ ‎∵点A，C到直线GH的距离相等，‎ ‎∴直线GH过线段AC的中点M（，﹣）．‎ ‎∴直线GH的解析式为y=﹣x﹣1，‎ ‎∴G（﹣，），‎ ‎∴存在点G（﹣，）或G（﹣1，﹣4）．‎ ‎（3）解法一：‎ 如图③，∵E（﹣2，0），‎ ‎∴D的横坐标为﹣2，‎ ‎∵点D在抛物线上，‎ ‎∴D（﹣2，﹣3），‎ ‎∵F是OC中点，‎ ‎∴F（0，﹣），‎ ‎∴直线DF的解析式为：y=x﹣，‎ 则它与x轴交于点Q（2，0），‎ 则QB=QD，得∠QBD=∠QDB，∠BPE+∠EPF+∠FPD=∠DFP+∠PDF+∠FPD=180°，‎ ‎∵∠EPF=∠PDF，‎ ‎∴∠BPE=∠DFP，‎ ‎∴△PBE∽△FDP，‎ ‎∴，‎ 得：PB•DP=，‎ ‎∵PB+DP=BD=，‎ ‎∴PB=，‎ 即P是BD的中点，‎ 连接DE，‎ ‎∴在Rt△DBE中，PE=BD=．‎ 解法二：‎ 可知四边形ABDC为等腰梯形，取BD的中点P′，‎ P′F=（OB+CD）=，‎ P′F∥CD∥AB，‎ 连接EF，可知EF=DF=，‎ 即EF=FP′=FD，‎ 即△FEP′相似△FP′D，‎ 即∠EP′F=∠FP′D=∠FDP′，‎ 即∠EP′F和∠EPF重合，‎ 即P和P′重合，‎ P为BC中点，‎ PE=BD=（△BDE为直角三角形）．‎ ‎【点评】此题考查了待定系数法求二次函数的解析式，直线与二次函数的交点问题以及三角形面积问题的求解等知识．此题综合性很强，难度较大，解题的关键是注意数形结合思想、分类讨论思想与方程思想的应用