上海中考九年级数学知识点分类讲解 13页

九年级年级数学学科 相似三角形 知识点1：相似形 ‎1．图形的放大或缩小，称为图形的放缩运动．‎ ‎2．将一个图形放大或缩小后，就得到与它形状相同的图形．‎ ‎3．形状相同的两个图形叫做相似的图形，即相似形．‎ ‎【总结】‎ ‎1．相似图形的大小不一定相同，如果两个相似图形的大小相同，则两个相似形全等，当两个多边形 是全等形时，它们的对应边的长度的比值都是1；‎ ‎2．对于大小不同的两个相似图形，可以看作是大（小）的图形由小（大）的图形放大（缩小）得到．‎ ‎4．如果两个多边形是相似形，那么这两个多边形的对应角相等，对应边的长度成比例．‎ ‎【注意】‎ ‎1．理解相似多边形的定义，明确“对应”关系； ‎ ‎2．多边形的相似，要求边数相同，形状相同（对应角相等，对应边的长度成比例）．‎ 知识点2：比例线段 ‎1．一般来说，两个数或两个同类的量与相除，叫做与的比，记作：（或），其中．‎ 除以所得的商叫做与的比值．如果：的比值等于，那么．‎ ‎2．两条线段的长度的比叫做两条线段的比．‎ ‎3．如果（或），那么就说成比例．其中叫做第一比例项，叫做第二比例 项；叫做第三比例项；叫做第四比例项．‎ ‎4．在四条线段中，如果其中两条线段的比与另两条线段的比相等，那么这四条线段叫做成比例线段，简 称比例线段．‎ ‎【注意】‎ 要注意比例线段的顺序性与单位要统一．‎ ‎5．如果比例的两个内项（或两个外项）相同，那么这个相同的项叫做比例中项．如 ‎（）时，叫做和的比例中项．、、满足：．‎ ‎ 【注意】比例中项的应用一定要注意题目中的表述：比如题目中若出现“线段”或“单位”时，‎ 值为正值；否则，取正、负两个值．‎ ‎6．比例的基本性质：‎ ‎（1）如果，那么． ‎ ‎（2）比例线段的比例式中，只要乘积形式不变，的位置可以灵活变化． ‎ 若，则、、、、、、．‎ ‎【思考】判断命题“如果，那么”是真命题还是假命题，为什么？‎ ‎7．合比性质：如果，那么； ‎ ‎ 如果，那么；‎ ‎ 如果，那么；‎ ‎ 如果，那么．‎ ‎8．等比性质：如果，那么（）；‎ 如果，那么（）．‎ ‎【注意】等比性质的存在条件．‎ ‎9．如果点把线段分割成和（>）两段，其中是和的比例中项，那么称这 种分割为黄金分割．点称为线段的黄金分割点．与的比值称为黄金分割数，它的近似值为． ‎ ‎　‎ ‎【注意】‎ ‎1．一般来说，一条线段的黄金分割点有两个；‎ ‎2．利用黄金分割时一定是： ．‎ 知识点3：三角形一边的平行线 ‎1．三角形一边的平行线性质定理：平行于三角形一边的直线截其他两边所在的直线，截得的对应线段成 比例． ‎ ‎2．三角形一边的平行线性质定理推论：平行于三角形一边的直线截其他两边所在的直线，截得的三角形 ‎ 的三边与原三角形的三边对应成比例．‎ ‎3．三角形一边的平行线判定定理：如果一条直线截三角形的两边所得的对应线段成比例，那么这条直线 平行于三角形的第三边．‎ ‎4．三角形一边的平行线判定定理推论：如果一条直线截三角形的两边的延长线（这两边的延长线在第三 边的同侧）所得的对应线段成比例，那么这条直线平行于三角形的第三边．‎ ‎【总结】‎ 三角形一边平行线的定理可以理解为两个基本图形：“”字形与“8”字形．‎ ‎【注意】在运用判定定理时一定要是两边上的比才能得平行。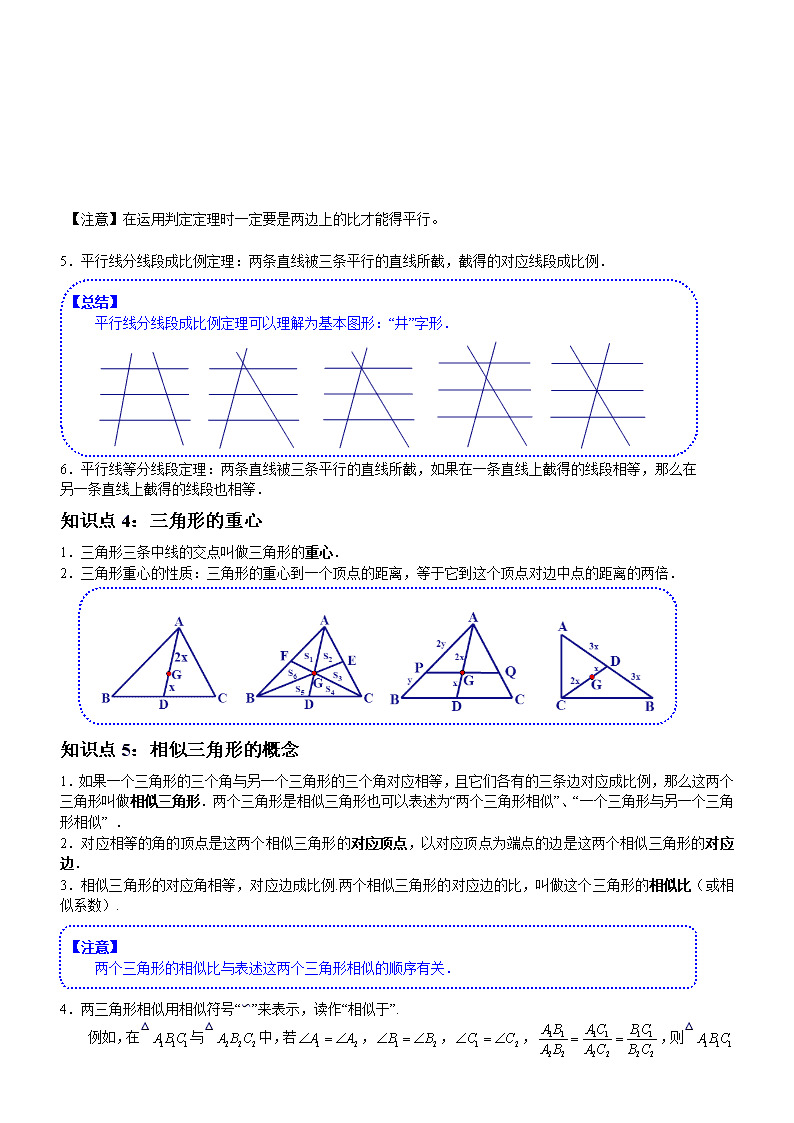‎ ‎5．平行线分线段成比例定理：两条直线被三条平行的直线所截，截得的对应线段成比例．‎ ‎【总结】‎ 平行线分线段成比例定理可以理解为基本图形：“井”字形．‎ ‎ ‎ ‎6．平行线等分线段定理：两条直线被三条平行的直线所截，如果在一条直线上截得的线段相等，那么在 另一条直线上截得的线段也相等．‎ 知识点4：三角形的重心 ‎1．三角形三条中线的交点叫做三角形的重心．‎ ‎2．三角形重心的性质：三角形的重心到一个顶点的距离，等于它到这个顶点对边中点的距离的两倍．‎ ‎ ‎ ‎ ‎ ‎ ‎ 知识点5：相似三角形的概念 ‎1．如果一个三角形的三个角与另一个三角形的三个角对应相等，且它们各有的三条边对应成比例，那么这两个三角形叫做相似三角形．两个三角形是相似三角形也可以表述为“两个三角形相似”、“一个三角形与另一个三角形相似” ．‎ ‎2．对应相等的角的顶点是这两个相似三角形的对应顶点，以对应顶点为端点的边是这两个相似三角形的对应边．‎ ‎3．相似三角形的对应角相等，对应边成比例.两个相似三角形的对应边的比，叫做这个三角形的相似比（或相似系数）.‎ ‎【注意】‎ ‎ 两个三角形的相似比与表述这两个三角形相似的顺序有关．‎ ‎4．两三角形相似用相似符号“∽”来表示，读作“相似于”.‎ 例如，在△与△中，若，，，，则△‎ 与△相似，其中点与点、点与点、点与点分别是对应点，记作△∽△．‎ ‎【注意】‎ 用符号表示两个三角形相似时，通常把对应顶点的字母分别写在三角形记号“△”后的相应位置上.‎ 思考：用符号表示两个相似三角形相似时，通常把对应顶点的字母分别写在三角形记号“△”后的相应的位置上.所以 ∽ 就一定意味着点“”与点“”的对应关系么？‎ 若已知“△∽△”或“△相似于△”，除非题目中给出点的对应关系，否则不能够确定点与点、点与点、点与点分别是对应点．‎ ‎ 【总结】‎ ‎ 全等三角形是相似三角形的特例. 当两个相似三角形的相似比时，这两个相似三角形就成为全等三角形.两个全等三角形一定是相似三角形；两个相似三角形不一定是全等三角形．‎ 知识点6：相似三角形的判定 ‎1．三角形相似的传递性：如果两个三角形分别与同一个三角形相似，那么这两个三角形也相似．‎ ‎2．相似三角形的预备定理：平行于三角形一边的直线截其他两边所在的直线，截得的三角形与原三角形相似．‎ ‎ 【总结】‎ ‎ 直线截△两边、两边所在的直线，截得的三角形与原三角形△相似.‎ ‎3．相似三角形判定定理1：如果一个三角形的两角与另一个三角形的两角对应相等，那么这两个三角形相似．简述为：两角对应相等，两个三角形相似．‎ 相似三角形判定定理2：如果一个三角形的两边与另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似．简述为：两边对应成比例且夹角相等，两个三角形相似．‎ 相似三角形判定定理3：如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．简述为：三边对应成比例，两个三角形相似．‎ ‎4．直角三角形相似的判定定理：如果一个直角三角形的斜边及一条直角边与另一个直角三角形的斜边及一条直角边对应成比例，那么这两个直角 三角形相似.简述为：斜边和直角边对应成比例，两个直角三角形相似.‎ ‎【记忆技巧】‎ 类比全等三角形的判定“、”、“”、“”、“”，相似的判定可以对照来理 解记忆.‎ ‎【注意】‎ 通过相似的判定应明确：相似只是图形的放缩，与位置无关．‎ 两个三角形中，如果一个三角形的两边和其中一边上的中线与另一个三角形的对应部分成比例，那么这两个三角形相似．‎ 注意：因为三角形的高线可能不在三角形内部，所以高线不具备相关的判定推论．‎ 知识点7：相似三角形的性质 1． 当我们知道两个三角形是相似的，我们能得到什么结论呢？‎ ‎ 根据相似三角形的定理，我们可以直接得到相似三角形最基本的性质：‎ ‎ 相似三角形的对应角相等，对应边成比例．‎ ‎ ‎ ‎【思考】 我们一般从哪些角度来讨论一个三角形？‎ ‎ 我们一般从角和边两方面出发来讨论三角形，当我们知道边角的对应关系之后，那么相关的对应高、对应中线、对应角平分线的比，分别与相似比有什么关系呢？‎ ‎【总结】‎ ‎ 我们由相似三角形的对应角相等，对应边成比例可以联想到它们对应的特殊线段及周长、面积，这样就形成了对于“对应特殊线段的比”、“周长比”、“面积比”分别与相似比之间的关系进行研究探索的三个问题.整个相似三角形性质的学习内容，就是围绕这些问题展开.‎ ‎【注意】‎ ‎“相似比”是揭示相似三角形本质特征与重要性质的一个基本概念，也是有关几何证明与计算中经常运用的一个数值．‎ ‎2. 我们利用相似三角形的判定和相似三角形的基本性质可以得到：‎ 相似三角形性质定理1 相似三角形对应高的比、对应中线的和对应角平分线的比都等于相似比.‎ 三角形的周长是三边之和，面积可用一边及这边上的高来表示，可见两个相似三角形的周长比、面积比与相似比之间有直接关系：‎ 相似三角形性质定理2 相似三角形的周长之比等于相似比.‎ 相似三角形性质定理3 相似三角形的面积的比等于相似比的平方.‎ ‎ 全等三角形的性质 ‎ 相似三角形的性质 全等三角形的对应角相等，对应边相等．‎ 全等三角形对应高、对应中线的和对应角平分线都相等 全等三角形的周长相等.‎ 全等三角形的面积相等.‎ 相似三角形的对应角相等，对应边成比例．‎ 相似三角形对应高的比、对应中线的和对应角平分线的比都等于相似比.‎ 相似三角形的周长之比等于相似比.‎ 相似三角形的面积的比等于相似比的平方.‎ 知识点8：向量的有关概念 ‎1．规定了方向的线段叫做有向线段．有向线段的方向是从一点到另一点的指向，这时线段的两个端点有顺序，我们把前一点叫做起点，另一点叫做终点，画图时在终点处画上箭头表示它的方向．‎ ‎【思考】我们知道线段与线段是一样的，那么有向线段与有向线段一样吗？如果不一样，那么它们有什么差别？‎ ‎2．既有大小、又有方向的量叫做向量．向量的大小也叫做向量的长度（或向量的模）．‎ ‎【思考】在数学中，时间和速度都是向量吗？‎ ‎3．向量的表示 ‎（1）向量可以用有向线段表示，有向线段的长度就表示向量的长度，有向线段的方向就表示向量的方向．如果有向线段表示一个向量，通常就直接说向量．这个向量的长度记作，它是一个数量；‎ ‎（2）向量还可以用一个小写的英文字母在上方加箭头表示，如、、、……．向量的长度记作．‎ ‎【注意】‎ ‎（1）用有向线段表示向量时，通常与有向线段的位置无关，我们把有向线段的起点和终点称为它所表示的向量的起点和终点；‎ ‎（2）两条不同的有向线段分别表示的向量，我们就说是“两个向量”．‎ 知识点9：向量的线性运算 1. 方向相同且长度相等的两个向量叫做相等的向量．‎ ‎2．方向相反且长度相等的两个向量叫做互为相反向量．向量的相反向量用表示．‎ ‎3．方向相同或相反的两个向量叫做平行向量．‎ ‎【思考】向量与是什么关系？‎ ‎4．一般地，我们把长度为零的向量叫做零向量，记作．‎ ‎ 规定的方向可以是任意的（或者说不确定）；．‎ ‎5．长度为1的向量叫做单位向量．设为单位向量，则．‎ ‎ 对于任意非零向量，与它同方向的单位向量记作，则，．‎ ‎【注意】‎ ‎（1）表示一个向量，0表示一个数量，它们是不一样的；‎ ‎（2）单位向量有无数个，不同的单位向量是指它们的方向不同．‎ ‎1．零向量的方向是任意的，与任何向量都平行．‎ ‎2．平行向量 ‎（1）平行向量不具有传递性，即根据∥，∥，只有在时才可以得到∥；‎ ‎（2）方向相同或相反的两个向量叫做平行向量，也可以叫做共线向量；‎ ‎（3）当向量∥时，直线与直线的位置关系有两种：平行或共线．‎ 锐角的三角比 知识点1：锐角的三角比 ‎1．如图，在△中，，直角边和分别叫做的对边和邻边．‎ ‎2．（1）直角三角形中一个锐角的对边与斜边的比叫做这个锐角的正弦．‎ ‎．‎ ‎（2）直角三角形中一个锐角的邻边与斜边的比叫做这个锐角的余弦．‎ ‎．‎ ‎（3）直角三角形中一个锐角的对边与邻边的比叫做这个锐角的正切．‎ ‎．‎ ‎ （4）直角三角形中一个锐角的邻边与对边的比叫做这个锐角的余切．‎ ‎．‎ ‎【记忆技巧】‎ 正（正对）弦（斜边）：对边比斜边； 余（余邻—“鱼鳞”）弦（斜边）：邻边比斜边．‎ 知识点2：特殊角的三角比 ‎1．特殊角的锐角三角比：‎ ‎【记忆技巧】‎ ‎1．图形推导法 ‎ ‎2．表格记忆法 ‎30°‎ ‎45°‎ ‎60°‎ ‎1‎ ‎1‎ ‎ ‎ 知识点3：解直角三角形 ‎1．在直角三角形中，由已知元素求未知元的过程叫做解直角三角形．‎ ‎2．在△中，90°，则它的三条边和两个锐角这五个元素间有以下关系：‎ ‎（1）锐角之间的关系：90°；‎ ‎（2）三边之间的关系：；‎ ‎（3）边角之间的关系：；；；．‎ 知识点4：解直角三角形的应用 ‎1．水平线：水平面上的直线以及和水平面平行的直线.‎ ‎2．铅垂线：垂直于水平面的直线，我们通常称为铅垂线.‎ ‎3．在测量时，如图，在视线与水平线所成的角中，视线在水平线上方的角叫做仰角，视线在水平线下方的角叫做俯角.‎ ‎4．如图，坡面的铅垂高度()和水平宽度()的比叫做坡面的坡度（或坡比），记作，即.‎ ‎ 坡度通常写成的形式，如1︰1.5．‎ ‎5．坡面与水平面的夹角叫做坡角,记作.‎ ‎ 坡度与坡角之间的关系: . ‎ ‎1．方向角：以观测者的位置为中心，将正北或正南方向作为起始方向，旋转到目标的方向线所成的小于 ‎90°的角，通常表达成北（南）偏东（西）* 度.若正好为45°，则表示为西（东）南（北）方向.‎ ‎2．方位角：从标准方向的北端起，顺时针方向到直线的水平角称为该直线的方位角.方位角的取值范围 为. ‎ 二次函数 知识点1：二次函数 一般的，解析式形如（其中是常数，且）的函数叫做二次函数．‎ ‎【总结】函数的定义给出了基本形式，因此我们通常可以用待定系数法去求解函数解析式，一般有几个未知系数就需要几个点的坐标来求解．‎ 知识点2：二次函数的基本性质 ‎1．抛物线（其中是常数，且）的对称轴是轴，即直线；顶点是原点．抛物线的开口方向由所取之的符号决定，当时，它的开口向上，顶点式抛物线的最低点；当时，它的开口向下，顶点式抛物线的最高点．‎ ‎【注意】‎ 抛物线的对称轴是一条直线，答题时一定要写直线.‎ ‎2．抛物线（其中、是常数，且）的对称轴是轴，即直线；顶点坐标是（0，）.抛物线的开口方向由所取之的符号决定，当时，它的开口向上，顶点式抛物线的最低点；当时，它的开口向下，顶点式抛物线的最高点．‎ ‎3．抛物线（其中、是常数，且）的对称轴是过点（，0）且平行（或重合）于轴的直线，即直线；顶点坐标是（，0）．当时，它的开口向上，顶点式抛物线的最低点；当时，它的开口向下，顶点式抛物线的最高点．‎ ‎4．抛物线（其中、、是常数，且）的对称轴是过点（，0）且平行（或重合）于轴的直线，即直线；顶点坐标是（，）．当时，它的开口向上，顶点式抛物线的最低点；当时，它的开口向下，顶点式抛物线的最高点．‎ ‎【注意】‎ 在二次函数中，我们常常会做到平移的题目，一般我们在做平移时都会把二次函数化为顶点式来进行平移的求解。.‎ ‎【记忆技巧】‎ 一般地，我们通常做二次函数平移时都会记住“左加右减，上加下减”.其中左右和上下分别代表着平移的方向，若二次函数向左右平移，则在后进行加减，若二次函数向上下平移，则在后进行加减 ‎5．抛物线（其中、、是常数，且）的对称轴是直线，顶点坐标是（，），与轴交点为（0，）.当时，它的开口向上，顶点式抛物线的最低点；当时，它的开口向下，顶点式抛物线的最高点．‎ ‎6．一般地，对于抛物线，沿着轴正方向看，可见它的变化情况如下：‎ ‎ 当时，抛物线在对称轴（即直线）左侧部分是下降的，在对称轴的右侧部分是上升的；‎ ‎ 当时，抛物线在对称轴（即直线）左侧部分是上升的，在对称轴的右侧部分是下降的．‎ ‎【注意】‎ 图像的上升或下降，是对图像变化情况的直观描述.规定以轴正方向为参照，一般不说明.‎ 圆 知识点1：圆和扇形 ‎1．用字母表示圆的周长，表示直径长，表示半径长，那么．‎ ‎2．圆上任意两点之间的部分叫做弧．‎ ‎3．设圆的半径长为，圆心角所对的弧长是，那么．‎ ‎4．设圆的半径长为，面积为，那么．‎ ‎5．由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形．‎ ‎6．设组成扇形的半径长为，圆心角度数为，弧长是，那么．‎ 知识点2：圆的基本性质 一、圆的确定：‎ ‎（一）相关定义：‎ ‎1．圆是平面上到一个定点的距离等于定长的所有点所成的图形．‎ ‎ 这个定点是圆心．‎ ‎ 联结圆心和圆上任意一点的线段是圆的半径．‎ ‎ 这个定长是圆的半径长．‎ ‎2．在圆所在的平面上，以圆周为分界线，含圆心的部分叫做圆的内部（简称圆内）；‎ ‎ 不含圆心的部分叫做圆的外部（简称圆外）．‎ ‎【总结】‎ 圆既是中心对称图形，又是轴对称图形，其对称中心为圆心，对称轴为过圆心的直线．‎ ‎（二）点与圆的位置关系：‎ ‎1．一般来说，对于给定的一个圆，平面上的点与这个圆的位置关系有三种：点在圆内、点在圆上、点在圆外．‎ ‎2．设一个圆的半径长为，点到圆心的距离为，则 点在圆外；‎ 点在圆上；‎ 点在圆内．‎ ‎（三）圆的确定：‎ ‎1．定理：不在同一直线上的三点确定一个圆．‎ ‎2．三角形的三个顶点确定一个圆．‎ 经过一个三角形各顶点的圆叫做这个三角形的外接圆，外接圆的圆心叫做这个三角形的外心，这个三角形叫做圆的内接三角形．‎ ‎3．如果一个圆经过一个多边形的各顶点，那么这个圆叫做这个多边形的外接圆，这个多边形叫做这个圆的内接多边形．‎ 二、圆心角、弧、弦、弦心距之间的关系：‎ ‎（一）相关定义：‎ ‎1．圆上任意两点之间的部分叫做圆弧，简称弧．‎ ‎2．联结圆上任意两点的线段叫做弦．‎ 过圆心的弦就是直径．‎ ‎3．以圆心为顶点的角叫做圆心角．‎ ‎4．圆的任意一条直径的两个端点将圆分成两条弧，每一条弧都叫做半圆．‎ ‎5．大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧．‎ ‎6．圆心到弦的距离叫做弦心距．‎ ‎（二）相关定理：‎ ‎1．定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等．‎ ‎2．推论：在同圆或等圆中，如果两个同心角、两条劣弧（或优弧）、两条弦、两条弦的弦心距得到的四组量中有一组量相等，那么它们所应的其余三组量也分别相等．‎ 三、垂径定理：‎ ‎1．垂径定理：如果圆的一条直径垂直于一条弦，那么这条直径平分这条弦，并且平分这条弦所对的弧．‎ ‎2．垂径定理推论1：如果圆的直径平分弦（这条弦不是直径），那么这条直径垂直于这条弦，并且平分 ‎ 这条弦所对的弧．‎ ‎3．垂径定理推论2：如果圆的直径平分弧，那么这条直径就垂直平分这条弧所对的弦．‎ ‎4．垂径定理推论3：如果一条直线是弦的垂直平分线，那么这条直线经过圆心，并平分这条弦所对的弧。‎ ‎5．垂径定理推论4：如果一条直线平分弦和弦所对的一条弧，那么这条直线经过圆心，并且垂直于这条 弦．‎ ‎6．垂径定理推论5：如果一条直线垂直于弦，并且平分弦所对的一条弧，那么这条直线经过圆心，并且 平分这条弦．‎ 知识点3：直线和圆的位置关系 一、基础定义：‎ ‎1．当直线与圆没有公共点时，叫做直线与圆相离．‎ ‎2．当直线与圆有唯一公共点时，叫做直线与圆相切，‎ 这时直线叫做圆的切线．‎ 唯一的公共点叫做切点．‎ ‎3．当直线与圆有两个公共点（即交点）时，叫做直线与圆相交．‎ 这时直线叫做圆的割线．‎ ‎4．根据直线与圆公共点个数的情况，相应得到直线与圆的位置关系有三种：相离，相切，相交．‎ 二、直线与圆位置关系用数量关系描述：‎ ‎ 如果的半径长为，圆心到直线的距离为 直线与⊙相交；‎ 直线与⊙相切；‎ 直线与⊙相离.‎ 三、相关定理：‎ ‎1．切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．‎ 知识点4：圆和圆的位置关系 一、相关定义：‎ ‎1．外离：两个圆没有公共点，并且每个圆上的点都在另一个圆的外部，叫做这两个圆外离． ‎ ‎2．外切：两个圆有唯一的公共点，并且除了这个公共点以外，每个圆上的点都在另一个圆的外部，叫做这两个圆外切．这个唯一的公共点叫做切点．‎ ‎3．相交：两个圆有两个公共点，叫做这两个圆相交．‎ ‎4．内切：两个圆有唯一的公共点，并且除了这个公共点以外，一个圆上的点都在另一个圆的内部，叫做 这两个圆内切，这个唯一的公共点叫做切点．‎ ‎5．内含：两个圆没有公共点，并且一个圆上的点都在另一个圆的内部，叫做这两个圆内含.当两个圆的圆 心重合时，称它们为同心圆．‎ ‎6．圆心距：两个圆的圆心之间的距离叫做圆心距．‎ ‎7．连心线：经过两个圆的圆心的直线叫做连心线．‎ 二、两圆位置关系：‎ ‎1．半径不等的两圆的位置关系：‎ 半径不等的两圆的半径分别为和，圆心距为，则两圆的位置关系可用、和之间的 数量关系表达，具体表达如下：‎ ‎①两圆外离；‎ ‎②两圆外切；‎ ‎③两圆相交；‎ ‎④两圆内切；‎ ‎⑤两圆内含．‎ ‎2．半径相等的两圆的位置关系有：外离、外切、相交、重合．‎ ‎【总结】‎ ‎1．半径不等两圆的位置关系用数轴表示：‎ ‎2．从两圆公共点个数考虑：‎ 交点个数 半径不等 半径相等 两圆无交点 两圆外离 两圆内含（同心圆）‎ 两圆外离 两圆有一个交点 两圆外切 两圆内切 两圆外切 两圆有两个交点 两圆相交 两圆相交 两圆有无数个交点 ‎——‎ 两圆重合 三、相关定理：‎ ‎1．相交两圆的连心线垂直平分两圆的公共弦．‎ ‎2．相切两圆的连心线经过切点．‎ ‎【结论】‎ 两圆的连心线是两圆的公共对称轴．‎ 知识点5：正多边形和圆 ‎1．各边相等，各角也相等的多边形叫做正多边形．‎ ‎2．有条边的正多边形（是正整数，且）就称作正边形．‎ ‎3．正多边形的外接圆（或内切圆）的圆心叫做正多边形的中心．‎ ‎4．正多边形的外接圆的半径叫做正多边形的半径．‎ ‎5．正多边形的内切圆的半径长叫做正多边形的边心距．‎ ‎6．正多边形一边所对的关于外接圆的圆心角叫做正多边形的中心角．‎ ‎【总结】‎ ‎1．正边形，若是奇数，则正边形是轴对称图形；‎ ‎ 若是偶数，则正边形既是轴对称图形，又是中心对称图形．‎ ‎2．正边形的条对称轴交于一点，其外接圆和内切圆的圆心都是这个正边形的对称轴的交点．这个交点到正边形的各顶点的距离相等，到正边形各边的距离也相等．‎ ‎ ‎