- 1.85 MB
- 2021-05-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
几何难题精选
解答题(共30小题)
1.(2015•河南)如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,= ;②当α=180°时,= .
(2)拓展探究
试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.
2.(2015•济南)如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.
(1)直接写出∠NDE的度数;
(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;
(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD=,其他条件不变,求线段AM的长.
3.(2015•岳阳)已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系: .
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PA•PB=k•AB.
4.(2015•重庆)在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E.DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
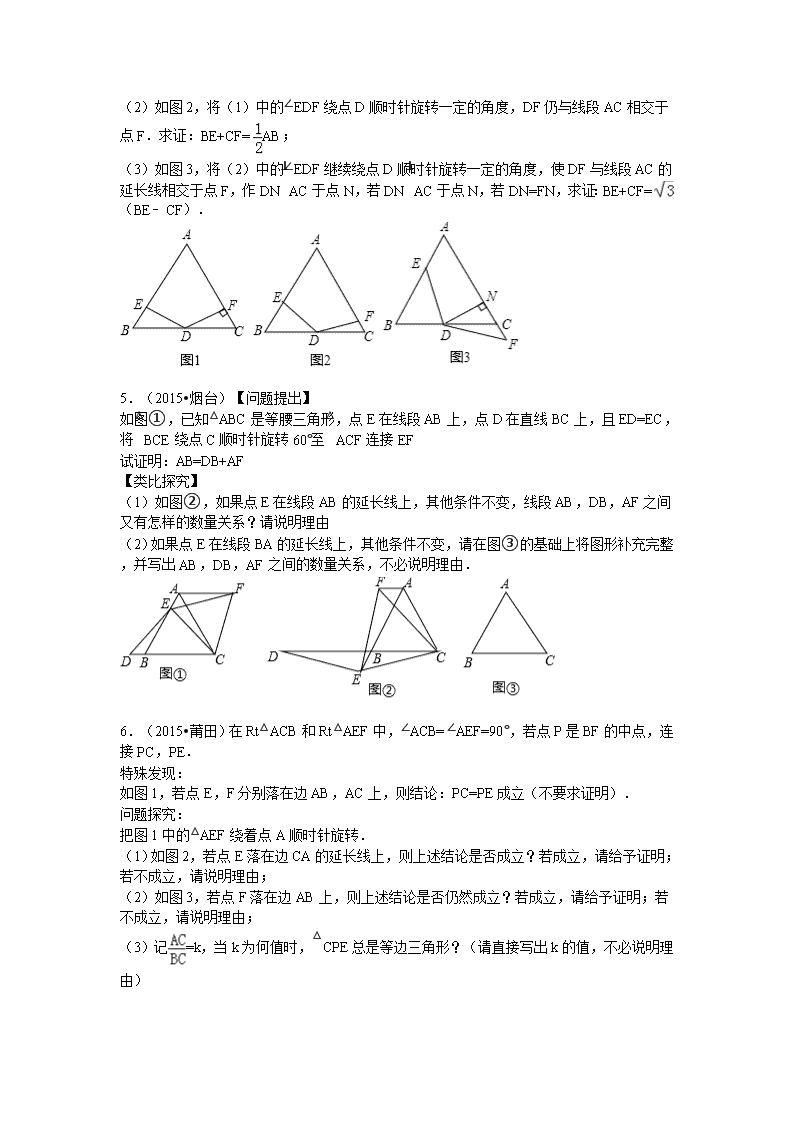
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=AB;
(3)如图3,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线相交于点F,作DN⊥AC于点N,若DN⊥AC于点N,若DN=FN,求证:BE+CF=(BE﹣CF).
5.(2015•烟台)【问题提出】
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
【类比探究】
(1)如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.
6.(2015•莆田)在Rt△ACB和Rt△AEF中,∠ACB=∠AEF=90°,若点P是BF的中点,连接PC,PE.
特殊发现:
如图1,若点E,F分别落在边AB,AC上,则结论:PC=PE成立(不要求证明).
问题探究:
把图1中的△AEF绕着点A顺时针旋转.
(1)如图2,若点E落在边CA的延长线上,则上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,若点F落在边AB上,则上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)记=k,当k为何值时,△CPE总是等边三角形?(请直接写出k的值,不必说明理由)
7.(2015•襄城区模拟)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;
(3)当∠1=∠2时,求直线PE的解析式;
(4)在(3)的条件下,直线PE上是否存在点M,使以M、A、G为顶点的三角形是等腰三角形?若存在,请直接写出M点坐标;若不存在,请说明理由.
8.(2015•重庆校级一模)已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,DF交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
(1)如图1,当点P与点G分别在线段BC与线段AD上时,若PC=1,计算出DG的长;
(2)如图1,当点P与点G分别在线段BC与线段AD上时,证明:四边形DFEP为菱形;
(3)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,(2)的结论:四边形DFEP为菱形是否依然成立?若成立,请给出证明;若不成立,请说明理由.
9.(2015•房山区二模)在△ABC中,AB=BC=2,∠ABC=90°,BD为斜边AC上的中线,将△ABD绕点D顺时针旋转α(0°<α<180°)得到△EFD,其中点A的对应点为点E,点B的对应点为点F.BE与FC相交于点H.
(1)如图1,直接写出BE与FC的数量关系: ;
(2)如图2,M、N分别为EF、BC的中点.求证:MN=;
(3)连接BF,CE,如图3,直接写出在此旋转过程中,线段BF、CE与AC之间的数量关系: .
10.(2015•衢州校级模拟)图1是边长分别为4和2的两个等边三角形纸片ABC和ODE叠放在一起(C与O重合).
(1)操作:固定△ABC,将△0DE绕点C顺时针旋转30°后得到△ODE,连结AD、BE,CE的延长线交AB于F(图2);
探究:在图2中,线段BE与AD之间有怎样的大小关系?试证明你的结论.
(2)在(1)的条件下将的△ODE,在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△PQR,当点P与点F重合时停止运动(图3)
探究:设△PQR移动的时间为x秒,△PQR与△ABC重叠部分的面积为y,求y与x之间的函数解析式,并写出函数自变量x的取值范围.
(3)将图1中△0DE固定,把△ABC沿着OE方向平移,使顶点C落在OE的中点G处,设为△ABG,然后将△ABG绕点G顺时针旋转,边BG交边DE于点M,边AG交边DO于点N,设∠BGE=α(30°<α<90°);(图4)
探究:在图4中,线段ON•EM的值是否随α的变化而变化?如果没有变化,请你求出ON•EM的值,如果有变化,请你说明理由.
11.(2015•武义县模拟)(1)将矩形OABC放在平面直角坐标系中,顶点O为原点,顶点C、A分别在x轴和y轴上,OA=8,OC=10,点E为OA边上一点,连结CE,将△EOC沿CE折叠.
①如图1,当点O落在AB边上的点D处时,求点E的坐标;
②如图2,当点O落在矩形OABC内部的点D处时,过点E作EG∥x轴交CD于点H,交BC于点G,设H(m,n),求m与n之间的关系式;
(2)如图3,将矩形OABC变为边长为10的正方形,点E为y轴上一动点,将△EOC沿CE折叠.点O落在点D处,延长CD交直线AB于点T,若=,求AT的长.
12.(2015•石家庄校级模拟)如图1,在菱形ABCD中,AC=6,BD=6,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别于边BC,CD相交于E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中是否存在线段EF最短,若存在,求出最小值,若不存在,请说明理由.
13.(2015春•泰安校级期中)如图,正方形OEFG绕着边长为30的正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.
(1)求证:OM=ON;
(2)设正方形OEFG的对角线OF与边AB相交于点P,连结PM.若PM=13,试求AM的长;
(3)连接MN,求△AMN周长的最小值,并指出此时线段MN与线段BD的关系.
14.(2014•天津)在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α.
(Ⅰ)如图①,当α=90°时,求AE′,BF′的长;
(Ⅱ)如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′;
(Ⅲ)若直线AE′与直线BF′相交于点P,求点P的纵坐标的最大值(直接写出结果即可).
15.(2014春•青山区期末)已知正方形ABCD和正方形EBGF共顶点B,连AF,H为AF的中点,连EH,正方形EBGF绕点B旋转.
(1)如图1,当F点落在BC上时,求证:EH=FC;
(2)如图2,当点E落在BC上时,连BH,若AB=5,BG=2,求BH的长;
(3)当正方形EBGF绕点B旋转到如图3的位置时,求的值.
16.(2013•盐城)阅读材料
如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.
解决问题
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出的值(用含α的式子表示出来)
17.(2013•梅州)用如图①,②所示的两个直角三角形(部分边长及角的度数在图中已标出),完成以下两个探究问题:
探究一:将以上两个三角形如图③拼接(BC和ED重合),在BC边上有一动点P.
(1)当点P运动到∠CFB的角平分线上时,连接AP,求线段AP的长;
(2)当点P在运动的过程中出现PA=FC时,求∠PAB的度数.
探究二:如图④,将△DEF的顶点D放在△ABC的BC边上的中点处,并以点D为旋转中心旋转△DEF,使△DEF的两直角边与△ABC的两直角边分别交于M、N两点,连接MN.在旋转△DEF的过程中,△AMN的周长是否存在有最小值?若存在,求出它的最小值;若不存在,请说明理由.
18.(2015•营口)如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
(1)求证:PC是⊙O的切线;
(2)若PD=,AC=8,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是的中点,连接CE,求CE的长.
19.(2015•永州)问题探究:
(一)新知学习:
圆内接四边形的判断定理:如果四边形对角互补,那么这个四边形内接于圆(即如果四边形EFGH的对角互补,那么四边形EFGH的四个顶点E、F、G、H都在同个圆上).
(二)问题解决:
已知⊙O的半径为2,AB,CD是⊙O的直径.P是上任意一点,过点P分别作AB,CD的垂线,垂足分别为N,M.
(1)若直径AB⊥CD,对于上任意一点P(不与B、C重合)(如图一),证明四边形PMON内接于圆,并求此圆直径的长;
(2)若直径AB⊥CD,在点P(不与B、C重合)从B运动到C的过程中,证明MN的长为定值,并求其定值;
(3)若直径AB与CD相交成120°角.
①当点P运动到的中点P1时(如图二),求MN的长;
②当点P(不与B、C重合)从B运动到C的过程中(如图三),证明MN的长为定值.
(4)试问当直径AB与CD相交成多少度角时,MN的长取最大值,并写出其最大值.
20.(2015•盘锦)如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
(1)请直接写出线段BE与线段CD的关系: ;
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0<α<360°),
①(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请说明理由;
②当AC=ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
21.(2015•朝阳)问题:如图(1),在Rt△ACB中,∠ACB=90°,AC=CB,∠DCE=45°,试探究AD、DE、EB满足的等量关系.
[探究发现]
小聪同学利用图形变换,将△CAD绕点C逆时针旋转90°得到△CBH,连接EH,由已知条件易得∠EBH=90°,∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°.
根据“边角边”,可证△CEH≌ ,得EH=ED.
在Rt△HBE中,由 定理,可得BH2+EB2=EH2,由BH=AD,可得AD、DE、EB之间的等量关系是 .
[实践运用]
(1)如图(2),在正方形ABCD中,△AEF的顶点E、F分别在BC、CD边上,高AG与正方形的边长相等,求∠EAF的度数;
(2)在(1)条件下,连接BD,分别交AE、AF于点M、N,若BE=2,DF=3,BM=2,运用小聪同学探究的结论,求正方形的边长及MN的长.
22.(2015•自贡)在△ABC中,AB=AC=5,cos∠ABC=,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1,求线段EF1长度的最大值与最小值的差.
23.(2015•吉林)两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).
(1)当点C落在边EF上时,x= cm;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,点M与点N之间距离的最小值.
24.(2015•汕尾)在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是边AB,AC的中点,若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)如图1,当α=90°时,线段BD1的长等于 ,线段CE1的长等于 ;(直接填写结果)
(2)如图2,当α=135°时,求证:BD1=CE1,且BD1⊥CE1;
(3)求点P到AB所在直线的距离的最大值.(直接写出结果)
25.(2015•赤峰)如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?
26.(2015•海南)如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点.
(1)求证:△ADP≌△ECP;
(2)若BP=n•PK,试求出n的值;
(3)作BM丄AE于点M,作KN丄AE于点N,连结MO、NO,如图2所示,请证明△MON是等腰三角形,并直接写出∠MON的度数.
27.(2015•丹东)在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.
(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=m•BP时,请直接写出PE与PF的数量关系.
28.(2015•成都)已知AC,EC分别是四边形ABCD和EFDC的对角线,点E在△ABC内,∠CAE+∠CBE=90°.
(1)如图①,当四边形ABCD和EFCG均为正方形时,连接BF.
(i)求证:△CAE∽△CBF;
(ii)若BE=1,AE=2,求CE的长;
(2)如图②,当四边形ABCD和EFCG均为矩形,且==k时,若BE=1,AE=2,CE=3,求k的值;
(3)如图③,当四边形ABCD和EFCG均为菱形,且∠DAB=∠GEF=45°时,设BE=m,AE=n,CE=p,试探究m,n,p三者之间满足的等量关系.(直接写出结果,不必写出解答过程)
29.(2015•锦州)如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是 ;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=AD,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
30.(2014•绵阳)如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.
几何难题精选(1) 旋转 圆 四边形
参考答案与试题解析
一.解答题(共30小题)
1.(2015•河南)如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,= ;②当α=180°时,= .
(2)拓展探究
试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.
【考点】几何变换综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)①当α=0°时,在Rt△ABC中,由勾股定理,求出AC的值是多少;然后根据点D、E分别是边BC、AC的中点,分别求出AE、BD的大小,即可求出的值是多少.
②α=180°时,可得AB∥DE,然后根据,求出的值是多少即可.
(2)首先判断出∠ECA=∠DCB,再根据,判断出△ECA∽△DCB,即可求出的值是多少,进而判断出的大小没有变化即可.
(3)根据题意,分两种情况:①点A,D,E所在的直线和BC平行时;②点A,D,E所在的直线和BC相交时;然后分类讨论,求出线段BD的长各是多少即可.
【解答】解:(1)①当α=0°时,
∵Rt△ABC中,∠B=90°,
∴AC=,
∵点D、E分别是边BC、AC的中点,
∴,
∴.
②如图1,,
当α=180°时,
可得AB∥DE,
∵,
∴=.
故答案为:.
(2)如图2,,
当0°≤α<360°时,的大小没有变化,
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵,
∴△ECA∽△DCB,
∴.
(3)①如图3,,
∵AC=4,CD=4,CD⊥AD,
∴AD==,
∵AD=BC,AB=DC,∠B=90°,
∴四边形ABCD是矩形,
∴.
②如图4,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P,,
∵AC=4,CD=4,CD⊥AD,
∴AD==,
∵点D、E分别是边BC、AC的中点,
∴DE==2,
∴AE=AD﹣DE=8﹣2=6,
由(2),可得
,
∴BD==.
综上所述,BD的长为4或.
【点评】(1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了相似三角形、全等三角形的判定和性质的应用,要熟练掌握.
(3)此题还考查了线段长度的求法,以及矩形的判定和性质的应用,要熟练掌握.
2.(2015•济南)如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.
(1)直接写出∠NDE的度数;
(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;
(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD=,其他条件不变,求线段AM的长.
【考点】几何变换综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)根据题意证明△MAC≌△NBC即可;
(2)与(1)的证明方法相似,证明△MAC≌△NBC即可;
(3)作GK⊥BC于K,证明AM=AG,根据△MAC≌△NBC,得到∠BDA=90°,根据直角三角形的性质和已知条件求出AG的长,得到答案.
【解答】解:(1)∵∠ACB=90°,∠MCN=90°,
∴∠ACM=∠BCN,
在△MAC和△NBC中,
,
∴△MAC≌△NBC,
∴∠NBC=∠MAC=90°,
又∵∠ACB=90°,∠EAC=90°,
∴∠NDE=90°;
(2)不变,
在△MAC≌△NBC中,
,
∴△MAC≌△NBC,
∴∠N=∠AMC,
又∵∠MFD=∠NFC,
∠MDF=∠FCN=90°,即∠NDE=90°;
(3)作GK⊥BC于K,
∵∠EAC=15°,
∴∠BAD=30°,
∵∠ACM=60°,
∴∠GCB=30°,
∴∠AGC=∠ABC+∠GCB=75°,
∠AMG=75°,
∴AM=AG,
∵△MAC≌△NBC,
∴∠MAC=∠NBC,
∴∠BDA=∠BCA=90°,
∵BD=,
∴AB=+,
AC=BC=+1,
设BK=a,则GK=a,CK=a,
∴a+a=+1,
∴a=1,
∴KB=KG=1,BG=,
AG=,
∴AM=.
【点评】本题考查的是矩形的判定和性质以及三角形全等的判定和性质,正确作出辅助线、利用方程的思想是解题的关键,注意旋转的性质的灵活运用.
3.(2015•岳阳)已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系: PA=PB .
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PA•PB=k•AB.
【考点】几何变换综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)根据三角形CBD是直角三角形,而且点P为线段CD的中点,应用直角三角形的性质,可得PA=PB,据此解答即可.
(2)首先过C作CE⊥n于点E,连接PE,然后分别判断出PC=PE、∠PCA=∠PEB、AC=BE;然后根据全等三角形判定的方法,判断出△PAC∽△PBE,即可判断出PA=PB仍然成立.
(3)首先延长AP交直线n于点F,作AE⊥BD于点E,然后根据相似三角形判定的方法,判断出△AEF∽△BPF,即可判断出AF•BP=AE•BF,再个AF=2PA,AE=2k,BF=AB,可得2PA•PB=2k.AB,所以PA•PB=k•AB,据此解答即可.
【解答】解:(1)∵l⊥n,
∴BC⊥BD,
∴三角形CBD是直角三角形,
又∵点P为线段CD的中点,
∴PA=PB.
(2)把直线l向上平移到如图②的位置,PA=PB仍然成立,理由如下:
如图②,过C作CE⊥n于点E,连接PE,
,
∵三角形CED是直角三角形,点P为线段CD的中点,
∴PD=PE,
又∵点P为线段CD的中点,
∴PC=PD,
∴PC=PE;
∵PD=PE,
∴∠CDE=∠PEB,
∵直线m∥n,
∴∠CDE=∠PCA,
∴∠PCA=∠PEB,
又∵直线l⊥m,l⊥n,CE⊥m,CE⊥n,
∴l∥CE,
∴AC=BE,
在△PAC和△PBE中,
∴△PAC≌△PBE,
∴PA=PB.
(3)如图③,延长AP交直线n于点F,作AE⊥BD于点E,,
∵直线m∥n,
∴,
∴AP=PF,
∵∠APB=90°,
∴BP⊥AF,
又∵AP=PF,
∴BF=AB;
在△AEF和△BPF中,
∴△AEF∽△BPF,
∴,
∴AF•BP=AE•BF,
∵AF=2PA,AE=2k,BF=AB,
∴2PA•PB=2k.AB,
∴PA•PB=k•AB.
【点评】(1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了直角三角形的性质和应用,要熟练掌握.
(3)此题还考查了全等三角形的判定和性质的应用,以及相似三角形的判定和性质的应用,要熟练掌握.
4.(2015•重庆)在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E.DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=AB;
(3)如图3,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线相交于点F,作DN⊥AC于点N,若DN⊥AC于点N,若DN=FN,求证:BE+CF=(BE﹣CF).
【考点】几何变换综合题;全等三角形的判定与性质;等边三角形的判定与性质;锐角三角函数的定义.菁优网版权所有
【专题】压轴题.
【分析】(1)如图1,易求得∠B=60°,∠BED=90°,BD=2,然后运用三角函数的定义就可求出BE的值;
(2)过点D作DM⊥AB于M,作DN⊥AC于N,如图2,易证△MBD≌△NCD,则有BM=CN,DM=DN,进而可证到△EMD≌△FND,则有EM=FN,就可得到BE+CF=BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD×cos60°=BD=BC=AB;
(3)过点D作DM⊥AB于M,如图3.同(1)可得:∠B=∠ACD=60°,同(2)可得:BM=CN,DM=DN,EM=FN.由DN=FN可得DM=DN=FN=EM,从而可得BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM,BE﹣CF=BM+EM﹣CF=BM+NF﹣CF=BM+NC=2BM.然后在Rt△BMD中,运用三角函数就可得到DM=BM,即BE+CF=(BE﹣CF).
【解答】解:(1)如图1,
∵AB=AC,∠A=60°,
∴△ABC是等边三角形,
∴∠B=∠C=60°,BC=AC=AB=4.
∵点D是线段BC的中点,
∴BD=DC=BC=2.
∵DF⊥AC,即∠AFD=90°,
∴∠AED=360°﹣60°﹣90°﹣120°=90°,
∴∠BED=90°,
∴BE=BD×cos∠B=2×cos60°=2×=1;
(2)过点D作DM⊥AB于M,作DN⊥AC于N,如图2,
则有∠AMD=∠BMD=∠AND=∠CND=90°.
∵∠A=60°,∴∠MDN=360°﹣60°﹣90°﹣90°=120°.
∵∠EDF=120°,∴∠MDE=∠NDF.
在△MBD和△NCD中,
,
∴△MBD≌△NCD,
∴BM=CN,DM=DN.
在△EMD和△FND中,
,
∴△EMD≌△FND,
∴EM=FN,
∴BE+CF=BM+EM+CF=BM+FN+CF=BM+CN
=2BM=2BD×cos60°=BD=BC=AB;
(3)过点D作DM⊥AB于M,如图3.
同(1)可得:∠B=∠ACD=60°.
同(2)可得:BM=CN,DM=DN,EM=FN.
∵DN=FN,∴DM=DN=FN=EM,
∴BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM,
BE﹣CF=BM+EM﹣CF=BM+NF﹣CF=BM+NC=2BM.
在Rt△BMD中,DM=BM•tanB=BM,
∴BE+CF=(BE﹣CF).
【点评】本题主要考查了等边三角形的判定与性质、四边形的内角和定理、全等三角形的判定与性质、三角函数的定义、特殊角的三角函数值等知识,通过证明三角形全等得到BM=CN,DM=DN,EM=FN是解决本题的关键.
5.(2015•烟台)【问题提出】
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
【类比探究】
(1)如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.
【考点】几何变换综合题.菁优网版权所有
【专题】压轴题.
【分析】首先判断出△CEF是等边三角形,即可判断出EF=EC,再根据ED=EC,可得ED=EF,∠CAF=∠BAC=60°,所以∠EAF=∠BAC+∠CAF=120°,∠DBE=120°,∠EAF=∠DBE;然后根据全等三角形判定的方法,判断出△EDB≌△FEA,即可判断出BD=AE,AB=AE+BF,所以AB=DB+AF.
(1)首先判断出△CEF是等边三角形,即可判断出EF=EC,再根据ED=EC,可得ED=EF,∠CAF=∠BAC=60°,所以∠EFC=∠FGC+∠FCG,∠BAC=∠FGC+∠FEA,∠FCG=∠FEA,再根据∠FCG=∠EAD,∠D=∠EAD,可得∠D=∠FEA;然后根据全等三角形判定的方法,判断出△EDB≌△FEA,即可判断出BD=AE,EB=AF,进而判断出AB=BD﹣AF即可.
(2)首先根据点E在线段BA的延长线上,在图③的基础上将图形补充完整,然后判断出△CEF是等边三角形,即可判断出EF=EC,再根据ED=EC,可得ED=EF,∠CAF=∠BAC=60°,再判断出∠DBE=∠EAF,∠BDE=∠AEF;最后根据全等三角形判定的方法,判断出△EDB≌△FEA,即可判断出BD=AE,EB=AF,进而判断出AF=AB+BD即可.
【解答】证明:ED=EC=CF,
∵△BCE绕点C顺时针旋转60°至△ACF,
∴∠ECF=60°,∠BCA=60°,BE=AF,EC=CF,
∴△CEF是等边三角形,
∴EF=EC,∠CEF=60°,
又∵ED=EC,
∴ED=EF,
∵△ABC是等腰三角形,∠BCA=60°,
∴△ABC是等边三角形,
∴∠CAF=∠CBA=60°,
∴∠EAF=∠BAC+∠CAF=120°,∠DBE=120°,∠EAF=∠DBE,
∵∠CAF=∠CEF=60°,
∴A、E、C、F四点共圆,
∴∠AEF=∠ACF,
又∵ED=EC,
∴∠D=∠BCE,∠BCE=∠ACF,
∴∠D=∠AEF,
在△EDB和△FEA中,
(AAS)
∴△EDB≌△FEA,
∴DB=AE,BE=AF,
∵AB=AE+BE,
∴AB=DB+AF.
(1)AB=BD+AF;
延长EF、CA交于点G,
∵△BCE绕点C顺时针旋转60°至△ACF,
∴∠ECF=60°,BE=AF,EC=CF,
∴△CEF是等边三角形,
∴EF=EC,
又∵ED=EC,
∴ED=EF,∠EFC=∠BAC=60°,
∵∠EFC=∠FGC+∠FCG,∠BAC=∠FGC+∠FEA,
∴∠FCG=∠FEA,
又∵∠FCG=∠ECD,∠D=∠ECD,
∴∠D=∠FEA,
由旋转的性质,可得
∠CBE=∠CAF=120°,
∴∠DBE=∠FAE=60°,
在△EDB和△FEA中,
(AAS)
∴△EDB≌△FEA,
∴BD=AE,EB=AF,
∴BD=FA+AB,
即AB=BD﹣AF.
(2)如图③,,
ED=EC=CF,
∵△BCE绕点C顺时针旋转60°至△ACF,
∴∠ECF=60°,BE=AF,EC=CF,BC=AC,
∴△CEF是等边三角形,
∴EF=EC,
又∵ED=EC,
∴ED=EF,
∵AB=AC,BC=AC,
∴△ABC是等边三角形,
∴∠ABC=60°,
又∵∠CBE=∠CAF,
∴∠CAF=60°,
∴∠EAF=180°﹣∠CAF﹣∠BAC
=180°﹣60°﹣60°
=60°
∴∠DBE=∠EAF;
∵ED=EC,
∴∠ECD=∠EDC,
∴∠BDE=∠ECD+∠DEC=∠EDC+∠DEC,
又∵∠EDC=∠EBC+∠BED,
∴∠BDE=∠EBC+∠BED+∠DEC=60°+∠BEC,
∵∠AEF=∠CEF+∠BEC=60°+∠BEC,
∴∠BDE=∠AEF,
在△EDB和△FEA中,
(AAS)
∴△EDB≌△FEA,
∴BD=AE,EB=AF,
∵BE=AB+AE,
∴AF=AB+BD,
即AB,DB,AF之间的数量关系是:
AF=AB+BD.
【点评】(1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了空间想象能力,考查了数形结合方法的应用,要熟练掌握.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握.
6.(2015•莆田)在Rt△ACB和Rt△AEF中,∠ACB=∠AEF=90°,若点P是BF的中点,连接PC,PE.
特殊发现:
如图1,若点E,F分别落在边AB,AC上,则结论:PC=PE成立(不要求证明).
问题探究:
把图1中的△AEF绕着点A顺时针旋转.
(1)如图2,若点E落在边CA的延长线上,则上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,若点F落在边AB上,则上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)记=k,当k为何值时,△CPE总是等边三角形?(请直接写出k的值,不必说明理由)
【考点】几何变换综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)首先过点P作PM⊥CE于点M,然后根据EF⊥AE,BC⊥AC,可得EF∥MP∥CB,推得,再根据点P是BF的中点,可得EM=MC,据此推得PC=PE即可.
(2)首先过点F作FD⊥AC于点D,过点P作PM⊥AC于点M,连接PD,然后根据全等三角形判定的方法,判断出△DAF≌△EAF,即可判断出AD=AE;再判断出△DAP≌△EAP,即可判断出PD=PE;最后根据FD⊥AC,BC⊥AC,PM⊥AC,可得FD∥BC∥PM,再根据点P是BF的中点,推得PC=PD,再根据PD=PE,即可推得PC=PE.
(3)首先根据△CPE总是等边三角形,可得将△AEF绕着点A顺时针旋转180°,△CPE仍是等边三角形;然后根据∠BCF=∠BEF=90°,点P是BF的中点,可得点C、E在以点P为圆心,BF为直径的圆上;最后根据圆周角定理,求出∠CBE的度数,即可求出当△CPE总是等边三角形时,k的值是多少.
【解答】解:(1)如图2,过点P作PM⊥CE于点M,
,
PC=PE成立,理由如下:
∵EF⊥AE,BC⊥AC,
∴EF∥MP∥CB,
∴,
∵点P是BF的中点,
∴EM=MC,
又∵PM⊥CE,
∴PC=PE.
(2)如图3,过点F作FD⊥AC于点D,过点P作PM⊥AC于点M,连接PD,
,
PC=PE成立,理由如下:
∵∠DAF=∠EAF,∠FDA=∠FEA=90°,
在△DAF和△EAF中,
,
∴△DAF≌△EAF(AAS),
∴AD=AE,
在△DAP和△EAP中,
,
∴△DAP≌△EAP(SAS),
∴PD=PE,
∵FD⊥AC,BC⊥AC,PM⊥AC,
∴FD∥BC∥PM,
∴,
∵点P是BF的中点,
∴DM=MC,
又∵PM⊥AC,
∴PC=PD,
又∵PD=PE,
∴PC=PE.
(3)如图4,,
∵△CPE总是等边三角形,
∴将△AEF绕着点A顺时针旋转180°,△CPE仍是等边三角形,
∵∠BCF=∠BEF=90°,点P是BF的中点,
∴点C、E在以点P为圆心,BF为直径的圆上,
∵△CPE是等边三角形,
∴∠CPE=60°,
根据圆周角定理,可得
∠CBE=∠CPE=60°=30°,
即∠ABC=30°,
在Rt△ABC中,
∵=k,=tan30°,
∴k=tan30°=,
∴当k为时,△CPE总是等边三角形.
【点评】(1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了全等三角形判定和性质的应用,以及直角三角形的性质和应用,要熟练掌握.
(3)解答第(3)题时,理解“△CPE总是等边三角形”的含义是解答此题的关键所在.
7.(2015•襄城区模拟)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;
(3)当∠1=∠2时,求直线PE的解析式;
(4)在(3)的条件下,直线PE上是否存在点M,使以M、A、G为顶点的三角形是等腰三角形?若存在,请直接写出M点坐标;若不存在,请说明理由.
【考点】几何变换综合题.菁优网版权所有
【分析】(1)由AO=AD,AG=AG,根据斜边和一条直角边对应相等的两个直角三角形全等,判断出△AOG≌△ADG即可.
(2)首先根据三角形全等的判定方法,判断出△ADP≌△ABP,再结合△AOG≌△ADG,可得∠DAP=∠BAP,∠1=∠DAG;然后根据∠1+∠DAG+∠DAP+∠BAP=90°,求出∠PAG的度数;最后判断出线段OG、PG、BP之间的数量关系即可.
(3)首先根据△AOG≌△ADG,判断出∠AGO=∠AGD;然后根据∠1+∠AGO=90°,∠2+∠PGC=90°,判断出当∠1=∠2时,∠AGO=∠AGD=∠PGC,而∠AGO+∠AGD+∠PGC=180°,求出∠1=∠2=30°;最后确定出P、G两点坐标,即可判断出直线PE的解析式.
(4)根据题意,分两种情况:①当点M在x轴的负半轴上时;②当点M在EP的延长线上时;根据以M、A、G为顶点的三角形是等腰三角形,求出M点坐标是多少即可.
【解答】(1)证明:在Rt△AOG和Rt△ADG中,
(HL)
∴△AOG≌△ADG.
(2)解:在Rt△ADP和Rt△ABP中,
∴△ADP≌△ABP,
则∠DAP=∠BAP;
∵△AOG≌△ADG,
∴∠1=∠DAG;
又∵∠1+∠DAG+∠DAP+∠BAP=90°,
∴2∠DAG+2∠DAP=90°,
∴∠DAG+∠DAP=45°,
∵∠PAG=∠DAG+∠DAP,
∴∠PAG=45°;
∵△AOG≌△ADG,
∴DG=OG,
∵△ADP≌△ABP,
∴DP=BP,
∴PG=DG+DP=OG+BP.
(3)解:∵△AOG≌△ADG,
∴∠AGO=∠AGD,
又∵∠1+∠AGO=90°,∠2+∠PGC=90°,∠1=∠2,
∴∠AGO=∠PGC,
又∵∠AGO=∠AGD,
∴∠AGO=∠AGD=∠PGC,
又∵∠AGO+∠AGD+∠PGC=180°,
∴∠AGO=∠AGD=∠PGC=180°÷3=60°,
∴∠1=∠2=90°﹣60°=30°;
在Rt△AOG中,
∵AO=3,
∴OG=AOtan30°=3×=,
∴G点坐标为(,0),CG=3﹣,
在Rt△PCG中,PC===3(﹣1),
∴P点坐标为:(3,3﹣3 ),
设直线PE的解析式为:y=kx+b,
则,
解得,
∴直线PE的解析式为y=x﹣3.
(4)①如图1,当点M在x轴的负半轴上时,,
∵AG=MG,点A坐标为(0,3),
∴点M坐标为(0,﹣3).
②如图2,当点M在EP的延长线上时,,
由(3),可得∠AGO=∠PGC=60°,
∴EP与AB的交点M,满足AG=MG,
∵A点的横坐标是0,G点横坐标为,
∴M的横坐标是2,纵坐标是3,
∴点M坐标为(2,3).
综上,可得
点M坐标为(0,﹣3)或(2,3).
【点评】(1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了空间想象能力,考查了数形结合方法的应用,要熟练掌握.
(2)此题还考查了全等三角形的判定和性质的应用,以及直线的解析式的求法,要熟练掌握.
(3)此题还考查了等腰三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:①等腰三角形的两腰相等.②等腰三角形的两个底角相等.③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
8.(2015•重庆校级一模)已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,DF交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
(1)如图1,当点P与点G分别在线段BC与线段AD上时,若PC=1,计算出DG的长;
(2)如图1,当点P与点G分别在线段BC与线段AD上时,证明:四边形DFEP为菱形;
(3)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,(2)的结论:四边形DFEP为菱形是否依然成立?若成立,请给出证明;若不成立,请说明理由.
【考点】几何变换综合题.菁优网版权所有
【分析】(1)作PM⊥DG于M,根据等腰三角形的性质由PD=PG得MG=MD,根据矩形的判定易得四边形PCDM为矩形,则PC=MD,于是有DG=2PC;
(2)根据四边形ABCD为正方形得AD=AB,由四边形ABPM为矩形得AB=PM,则AD=PM,再利用等角的余角相等得到∠GDH=∠MPG,于是可根据“ASA”证明△ADF≌△MPG,得到DF=PG,加上PD=PG,得到DF=PD,然后利用旋转的性质得∠EPG=90°,PE=PG,所以PE=PD=DF,再利用DF⊥PG得到DF∥PE,于是可判断四边形PEFD为平行四边形,加上DF=PD,则可判断四边形PEFD为菱形;
(3)与(1)中②的证明方法一样可得到四边形PEFD为菱形.
【解答】(1)证明:作PM⊥DG于M,如图1,
∵PD=PG,
∴MG=MD,
∵四边形ABCD为矩形,
∴PCDM为矩形,
∴PC=MD,
∴DG=2PC=2;
(2)∵四边形ABCD为正方形,
∴AD=AB,
∵四边形ABPM为矩形,
∴AB=PM,
∴AD=PM,
∵DF⊥PG,
∴∠DHG=90°,
∴∠GDH+∠DGH=90°,
∵∠MGP+∠MPG=90°,
∴∠GDH=∠MPG,
在△ADF和△MPG中,
,
∴△ADF≌△MPG(ASA),
∴DF=PG,
而PD=PG,
∴DF=PD,
∵线段PG绕点P逆时针旋转90°得到线段PE,
∴∠EPG=90°,PE=PG,
∴PE=PD=DF,
而DF⊥PG,
∴DF∥PE,
即DF∥PE,且DF=PE,
∴四边形PEFD为平行四边形,
∵DF=PD,
∴四边形PEFD为菱形;
(3)解:四边形PEFD是菱形.理由如下:
作PM⊥DG于M,如图2,
与(1)一样同理可证得△ADF≌△MPG,
∴DF=PG,
而PD=PG,
∴DF=PD,
∵线段PG绕点P逆时针旋转90°得到线段PE,
∴∠EPG=90°,PE=PG,
∴PE=PD=DF
而DF⊥PG,
∴DF∥PE,
即DF∥PE,且DF=PE,
∴四边形PEFD为平行四边形,
∵DF=PD,
∴四边形PEFD为菱形.
【点评】本题考查了四边形的综合题:熟练掌握平行四边形、矩形、菱形和正方形的判定与性质是解题的关键;同时会运用等腰三角形的性质和旋转的性质;会利用三角形全等解决线段相等的问题.
9.(2015•房山区二模)在△ABC中,AB=BC=2,∠ABC=90°,BD为斜边AC上的中线,将△ABD绕点D顺时针旋转α(0°<α<180°)得到△EFD,其中点A的对应点为点E,点B的对应点为点F.BE与FC相交于点H.
(1)如图1,直接写出BE与FC的数量关系: BE=FC ;
(2)如图2,M、N分别为EF、BC的中点.求证:MN=;
(3)连接BF,CE,如图3,直接写出在此旋转过程中,线段BF、CE与AC之间的数量关系: BF2+CE2=AC2 .
【考点】几何变换综合题.菁优网版权所有
【分析】(1)首先判断出BD=AD=CD,然后根据旋转的性质,判断出ED=FD,∠BDE=∠CDF;最后根据全等三角形的判定方法,判断出△BED≌△CFD,即可判断出BE=FC.
(2)首先连接BF,取BF中点G,连接MG、NG,判断出BE⊥CF;然后根据M为EF中点,G为BF中点,N为BC中点,判断出MG∥BE,MG=,NG∥FC,NG=;最后根据BE=FC,BE⊥FC,判断出MG=NG,∠MGN=90°,即△MGN为等腰直角三角形,即可判断出MN=.
(3)首先根据BE⊥FC,可得BF2+CE2=EF2+BC2=BH2+CH2+EH2+FH2;然后根据EF=AB,可得BF2+CE2=AB2+BC2=AC2,据此判断即可.
【解答】(1)解:∵AB=BC=2,∠ABC=90°,BD为斜边AC上的中线,
∴BD=AD=CD,
又∵ED=AD,FD=BD,
∴ED=FD,
∵∠BDE=∠FDE+∠α=90°+∠α,
∠CDF=∠CDB+∠α=90°+∠α,
∴∠BDE=∠CDF,
在△BED和△CFD中,
∴△BED≌△CFD,
∴BE=FC.
(2)证明:如图2,连接BF,取BF中点G,连接MG、NG,
,
∵△BED≌△CFD,
∴∠1=∠2,
又∵∠3=∠4,
∴∠FHE=∠FDE=90°,
∴BE⊥CF,
∵M为EF中点,G为BF中点,
∴MG∥BE,MG=,
∵G为BF中点,N为BC中点,
∴NG∥FC,NG=,
又∵BE=FC,BE⊥FC,
∴MG=NG,∠MGN=90°,
∴△MGN为等腰直角三角形,
∴MN=.
(3)解:由(2),可得BE⊥FC,
∴BF2=BH2+FH2,
CE2=CH2+EH2,
EF2=EH2+FH2,
BC2=BH2+CH2,
∴BF2+CE2=EF2+BC2=BH2+CH2+EH2+FH2,
∵EF=AB,
∴BF2+CE2=AB2+BC2=AC2,
∴BF2+CE2=AC2.
故答案为:BE=FC、BF2+CE2=AC2.
【点评】(1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了空间想象能力,考查了数形结合方法的应用,要熟练掌握.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握.
(3)此题还考查了直角三角形的性质和应用,以及勾股定理的应用,要熟练掌握.
(4)此题还考查了三角形中位线定理的应用,要熟练掌握,解答此题的关键是要明确:三角形的中位线平行于第三边,并且等于第三边的一半.
10.(2015•衢州校级模拟)图1是边长分别为4和2的两个等边三角形纸片ABC和ODE叠放在一起(C与O重合).
(1)操作:固定△ABC,将△0DE绕点C顺时针旋转30°后得到△ODE,连结AD、BE,CE的延长线交AB于F(图2);
探究:在图2中,线段BE与AD之间有怎样的大小关系?试证明你的结论.
(2)在(1)的条件下将的△ODE,在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△PQR,当点P与点F重合时停止运动(图3)
探究:设△PQR移动的时间为x秒,△PQR与△ABC重叠部分的面积为y,求y与x之间的函数解析式,并写出函数自变量x的取值范围.
(3)将图1中△0DE固定,把△ABC沿着OE方向平移,使顶点C落在OE的中点G处,设为△ABG,然后将△ABG绕点G顺时针旋转,边BG交边DE于点M,边AG交边DO于点N,设∠BGE=α(30°<α<90°);(图4)
探究:在图4中,线段ON•EM的值是否随α的变化而变化?如果没有变化,请你求出ON•EM的值,如果有变化,请你说明理由.
【考点】几何变换综合题.菁优网版权所有
【分析】(1)BE=AD,可通过证三角形BEC和ACD全等来得出.
(2)由于重合部分的面积无法直接求出,因此可用△RPQ的面积减去△RST的面积来求得(S、T为RP、RQ与AC的交点).△PRQ的面积易求得.关键是△RST的面积,三角形RST中,由于∠RTS=∠CTQ=60°﹣∠TCQ=30°,而∠R=60°,因此△RST是直角三角形,只需求出RS和ST的长即可.上面已经求得了∠QTC=∠QCT=30°,因此RT=RQ﹣QT=RQ﹣QC=3﹣x,然后根据△RTS中特殊角的度数即可得出RS和ST的长,进而可得出y,x的函数关系式.
(3)本题可通过证△GEM和△NGO相似来求解.
【解答】解:(1)BE=AD.
证明:∵△ABC与△DCE是等边三角形,
∴∠ACB=∠DCE=60°,CA=CB,CE=CD,
∴∠BCE=∠ACD,
在△BCE与△ACD中,
,
∴△BCE≌△ACD(SAS),
∴BE=AD;
(2)如图在△CQT中,
∵∠TCQ=30°∠RQP=60°,
∴∠QTC=30°,
∴∠QTC=∠TCQ,
∴QT=QC=x,
∴RT=2﹣x,
∵∠RTS+∠R=90°
∴∠RST=90°
∴y=(0≤x≤2).
(3)答:ON•EM的值不变,理由为:
证明:∵∠AGB=60°
∴∠MGE+∠NGO=120°
∵∠GNO+∠NGO=120°
∴∠MGE=∠GNO
∵∠E=∠O
∴△EMG∽△OGN
∴,
∴ON•EM=OG•EG=1.
【点评】此题考查了相似三角形的判定与性质,全等三角形的判定与性质以及一元二次方程的求解方法等知识.此题综合性很强,难度较大,解题的关键是方程思想与数形结合思想的应用.
11.(2015•武义县模拟)(1)将矩形OABC放在平面直角坐标系中,顶点O为原点,顶点C、A分别在x轴和y轴上,OA=8,OC=10,点E为OA边上一点,连结CE,将△EOC沿CE折叠.
①如图1,当点O落在AB边上的点D处时,求点E的坐标;
②如图2,当点O落在矩形OABC内部的点D处时,过点E作EG∥x轴交CD于点H,交BC于点G,设H(m,n),求m与n之间的关系式;
(2)如图3,将矩形OABC变为边长为10的正方形,点E为y轴上一动点,将△EOC沿CE折叠.点O落在点D处,延长CD交直线AB于点T,若=,求AT的长.
【考点】几何变换综合题.菁优网版权所有
【分析】(1)根据翻折变换的性质找出相等的线段,证明△EAD∽△DBC,根据相似三角形的性质得到成比例线段,代入求值即可;
(2)证明△EDH≌△CGH,得到DH=HG,在Rt△EDH中,根据勾股定理列出关于m、n的式子,整理得到答案;
(3)根据=,得到AE=EO,证明Rt△EDH≌Rt△CGH,得到TA=TD,根据勾股定理列式求值.
【解答】解:(1)由题意得,DE=OE,CD=OC=10,
在Rt△DBC中,BC=OA=8,CD=10,
由勾股定理得,BD=6,
∵∠A=∠EDC=∠B=90°,
∴△EAD∽△DBC,
∴=,即=,
解得,AE=3,则OE=5,
∴E(0,5);
(2)由题意得,DE=OE=n,EH=m,HG=10﹣m,
在△EDH和△CGH中,
,
∴△EDH≌△CGH,
∴DH=HG=10﹣m,
在Rt△EDH中,DE=n,EH=m,DH=10﹣m,
由勾股定理得m2=n2+(10﹣m)2,
整理得m=n2+5;
(3)如图3,连接ET,
∵=,∴AE=EO,
在△EAT和△EDT中,
,
∴Rt△EDH≌Rt△CGH,
∴TA=TD,
在Rt△TBC中,CT=10+AT,BT=10﹣AT,BC=10,
由勾股定理得,(10+AT)2=(10﹣AT)2+100,
解得AT=.
【点评】本题考查的是翻折变换的性质、相似三角形的判定和性质、全等三角形的判定和性质以及勾股定理的运用,灵活运用性质和定理,找准翻折变换对应的线段和角是解题的关键.
12.(2015•石家庄校级模拟)如图1,在菱形ABCD中,AC=6,BD=6,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别于边BC,CD相交于E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中是否存在线段EF最短,若存在,求出最小值,若不存在,请说明理由.
【考点】几何变换综合题.菁优网版权所有
【分析】(1)根据菱形的性质和勾股定理求出AB的长;
(2)①证明△EAC≌△FAD,得到AE=AF,根据等边三角形的判定得到结论;
(3)根据垂线段最短进行计算即可.
【解答】解:(1)∵AC=6,BD=6,
∴OA=3,BO=3,
∴AB==6;
(2)①△AEF是等边三角形,
∵OA=3,AB=6,
∴∠ABO=30°,
∴∠BAO=60°,
∵∠EAC+∠CAF=60°,∠FAD+∠CAF=60°,
∴∠EAC=∠FAD,
在△EAC和△FAD中,
,
∴△EAC≌△FAD,
∴AE=AF,又∠EAF=60°,
∴△AEF是等边三角形;
②当AE⊥BC时,AE最小,即线段EF最短,
在等边△ABC中,AB=6,
∴AE=3,
则当旋转至AE⊥BC时线段EF最短,最小值是3.
【点评】本题考查的是旋转变换的性质和菱形的性质,掌握菱形的四条边相等,对角线互相垂直是解题的关键.
13.(2015春•泰安校级期中)如图,正方形OEFG绕着边长为30的正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.
(1)求证:OM=ON;
(2)设正方形OEFG的对角线OF与边AB相交于点P,连结PM.若PM=13,试求AM的长;
(3)连接MN,求△AMN周长的最小值,并指出此时线段MN与线段BD的关系.
【考点】几何变换综合题.菁优网版权所有
【分析】(1)首先判断出∠OAM=∠OBN,∠AOM=∠BON,然后根据全等三角形的判定方法,判断出△AOM≌△BON,即可判断出OM=ON.
(2)首先根据全等三角形的判定方法,判断出△POM≌△PON,PN=PM=5;然后根据△AOM≌△BON,判断出BN=AM;最后在Rt△AMP中,根据AM2+AP2=PM2,求出AM的长是多少即可.
(3)首先根据在Rt△AMN中,AM2+AN2=MN2,判断出当x=6时,即AM=6时,线段MN的长度最小,并求出此时MN、AN的值,求出△AMN周长的最小值是多少;然后判断出MN是△ABD的中位线,即可判断出MN∥BD,且MN=.
【解答】(1)证明:在正方形ABCD中,∠OAM=∠OBN=45°,OA=OB,
∵∠AOM+∠AON=∠EOG=90°,∠BON+∠AON=∠AOB=90°,
∴∠AOM=∠BON,
在△AOM和△BON中,
∴△AOM≌△BON,
∴OM=ON.
(2)∵OF是正方形OEFG的对角线,
∴∠POM=∠PON,
在△POM和△PON中,
∴△POM≌△PON,
∴PN=PM=5,
∵△AOM≌△BON,
∴BN=AM,
设AM=BN=x,
则AP=AB﹣BN﹣PN=12﹣x﹣5=7﹣x,
在Rt△AMP中,
AM2+AP2=PM2,
即x2+(7﹣x)2=52,
整理,可得
x2﹣7x+12=0,
解得x1=3,x2=4,
所以AM的长为3或4.
(3)设AM=BN=x,
则AN=AB﹣BN=12﹣x,
在Rt△AMN中,
AM2+AN2=MN2,
即MN2=x2+(12﹣x)2=2(x﹣6)2+72
∴当x=6时,即AM=6时,线段MN的长度最小,
此时MN=,
AN=12﹣x=12﹣6=6,
∴△AMN周长的最小值是:
6+6+6=12+6,
∵点M是AD的中点,点N是AB的中点,
∴MN是△ABD的中位线,
∴MN∥BD,且MN=.
【点评】(1)此题主要考查了几何变换综合题,以及线段的最大值、最小值的求解,考查了分析推理能力,要熟练掌握.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握.
(3)此题还考查了直角三角形的性质和应用,以及三角形的中位线的性质和应用,要熟练掌握.
14.(2014•天津)在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α.
(Ⅰ)如图①,当α=90°时,求AE′,BF′的长;
(Ⅱ)如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′;
(Ⅲ)若直线AE′与直线BF′相交于点P,求点P的纵坐标的最大值(直接写出结果即可).
【考点】几何变换综合题;三角形的外角性质;全等三角形的判定与性质;含30度角的直角三角形;勾股定理.菁优网版权所有
【专题】综合题;压轴题.
【分析】(1)利用勾股定理即可求出AE′,BF′的长.
(2)运用全等三角形的判定与性质、三角形的外角性质就可解决问题.
(3)首先找到使点P的纵坐标最大时点P的位置(点P与点D′重合时),然后运用勾股定理及30°角所对的直角边等于斜边的一半等知识即可求出点P的纵坐标的最大值.
【解答】解:(Ⅰ)当α=90°时,点E′与点F重合,如图①.
∵点A(﹣2,0)点B(0,2),
∴OA=OB=2.
∵点E,点F分别为OA,OB的中点,
∴OE=OF=1
∵正方形OE′D′F′是正方形OEDF绕点O顺时针旋转90°得到的,
∴OE′=OE=1,OF′=OF=1.
在Rt△AE′O中,
AE′=.
在Rt△BOF′中,
BF′=.
∴AE′,BF′的长都等于.
(Ⅱ)当α=135°时,如图②.
∵正方形OE′D′F′是由正方形OEDF绕点O顺时针旋转135°所得,
∴∠AOE′=∠BOF′=135°.
在△AOE′和△BOF′中,
,
∴△AOE′≌△BOF′(SAS).
∴AE′=BF′,且∠OAE′=∠OBF′.
∵∠ACB=∠CAO+∠AOC=∠CBP+∠CPB,∠CAO=∠CBP,
∴∠CPB=∠AOC=90°
∴AE′⊥BF′.
(Ⅲ)∵∠BPA=∠BOA=90°,∴点P、B、A、O四点共圆,
∴当点P在劣弧OB上运动时,点P的纵坐标随着∠PAO的增大而增大.
∵OE′=1,∴点E′在以点O为圆心,1为半径的圆O上运动,
∴当AP与⊙O相切时,∠E′AO(即∠PAO)最大,
此时∠AE′O=90°,点D′与点P重合,点P的纵坐标达到最大.
过点P作PH⊥x轴,垂足为H,如图③所示.
∵∠AE′O=90°,E′O=1,AO=2,
∴∠E′AO=30°,AE′=.
∴AP=+1.
∵∠AHP=90°,∠PAH=30°,
∴PH=AP=.
∴点P的纵坐标的最大值为.
【点评】本题是在图形旋转过程中,考查了全等三角形的判定与性质、勾股定理、三角形的外角性质、30°角所对的直角边等于斜边的一半等知识,而找到使点P的纵坐标最大时点P的位置是解决最后一个问题的关键.
15.(2014春•青山区期末)已知正方形ABCD和正方形EBGF共顶点B,连AF,H为AF的中点,连EH,正方形EBGF绕点B旋转.
(1)如图1,当F点落在BC上时,求证:EH=FC;
(2)如图2,当点E落在BC上时,连BH,若AB=5,BG=2,求BH的长;
(3)当正方形EBGF绕点B旋转到如图3的位置时,求的值.
【考点】几何变换综合题;全等三角形的判定与性质;等腰三角形的判定与性质;直角三角形斜边上的中线;勾股定理;三角形中位线定理;正方形的性质.菁优网版权所有
【专题】压轴题.
【分析】(1)延长FE交AB于点Q,易证EF=QE,QB=FB,从而可以证到HE=AQ,AQ=CF,进而得到HE=CF.
(2)延长EH交AB于点N,易证△ANH≌△FEH,则有NH=EH,AN=EF,进而可以证到BH=EN,只需求出EN就可求出BH的值.
(3)过点A作EF平行线交EB的延长线于点T,延长EH交AT于S,连接SB、EC,易证△ASH≌△FEH,则有AS=EF,SH=EH.进而可以证到△SAB≌△EBC,则有SB=EC,∠ASB=∠BEC.由∠ASB=∠BEC可以推出∠SBE=∠CEF,从而可以证到△SBE≌△CEF,则有SE=CF,就可得到EH=SE=CF.
【解答】解:(1)证明:延长FE交AB于点Q,如图1,
∵四边形EFGB是正方形,
∴EF=EB,∠EFB=∠EBF=45°.
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC.
∴∠BQF=∠QBE=45°.
∴QE=EB.
∴QE=EF.
∵AH=FH,
∴HE=AQ.
∵∠BQF=∠BFQ=45°,
∴BQ=BF.
∵AB=BC,
∴AQ=CF.
∴HE=CF.
(2)延长EH交AB于点N,如图2,
∵四边形BEFG是正方形,
∴EF∥BG,EF=EB=BG=2.
∵EF∥AG,
∴∠FEH=∠ANH,∠EFH=∠NAH.
在△ANH和△FEH中,
∴△ANH≌△FEH.
∴NH=EH,AN=EF.
∵AB=5,AN=EF=2,
∴BN=AB﹣AN=3.
∵∠NBE=90°,BE=2,BN=3,
∴EN==.
∵∠NBE=90°,EH=NH,
∴BH=EN=.
∴BH的值为.
(3)过点A作EF平行线交EB的延长线于点T,
延长EH交AT于S,连接SB、EC,如图3,
∵EF∥AS,
∴∠FEH=∠ASH,∠EFH=∠SAH.
在△ASH和△FEH中,
∴△ASH≌△FEH.
∴AS=EF,SH=EH.
∵四边形BEFG是正方形,
∴BE=EF,∠FEB=90°.
∴AS=BE.
∵EF∥AS,
∴∠ATE=∠FEB=90°.
∴∠TAB+∠ABT=90°.
∵∠ABC=90°,
∴∠CBE+∠ABT=90°.
∴∠TAB=∠CBE.
在△SAB和△EBC中,
∴△SAB≌△EBC.
∴SB=EC.∠ASB=∠BEC.
∵∠ATB=90°,
∴∠TSB+∠TBS=90°.
∴∠ASB+∠SBE=360°﹣90°=270°.
∵∠BEC+∠CEF=360°﹣90°=270°,
∴∠SBE=∠CEF.
在△SBE和△CEF中,
.
∴△SBE≌△CEF.
∴SE=CF.
∵SH=EH,
∴EH=SE=CF.
∴的值为.
【点评】本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、正方形的性质、三角形的中位线定理、勾股定理、直角三角形斜边上的中线等于斜边的一半等知识,综合性非常强,有一定的难度.而利用点H为AF的中点构造全等三角形是解决第三小题的关键.
16.(2013•盐城)阅读材料
如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.
解决问题
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出的值(用含α的式子表示出来)
【考点】几何变换综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)如答图②所示,连接OC、OD,证明△BOF≌△COD;
(2)如答图③所示,连接OC、OD,证明△BOF∽△COD,相似比为;
(3)如答图④所示,连接OC、OD,证明△BOF∽△COD,相似比为tan.
【解答】解:(1)猜想:BF=CD.理由如下:
如答图②所示,连接OC、OD.
∵△ABC为等腰直角三角形,点O为斜边AB的中点,
∴OB=OC,∠BOC=90°.
∵△DEF为等腰直角三角形,点O为斜边EF的中点,
∴OF=OD,∠DOF=90°.
∵∠BOF=∠BOC+∠COF=90°+∠COF,∠COD=∠DOF+∠COF=90°+∠COF,
∴∠BOF=∠COD.
∵在△BOF与△COD中,
∴△BOF≌△COD(SAS),
∴BF=CD.
(2)答:(1)中的结论不成立.
如答图③所示,连接OC、OD.
∵△ABC为等边三角形,点O为边AB的中点,
∴=tan30°=,∠BOC=90°.
∵△DEF为等边三角形,点O为边EF的中点,
∴=tan30°=,∠DOF=90°.
∴==.
∵∠BOF=∠BOC+∠COF=90°+∠COF,∠COD=∠DOF+∠COF=90°+∠COF,
∴∠BOF=∠COD.
在△BOF与△COD中,
∵==,∠BOF=∠COD,
∴△BOF∽△COD,
∴=.
(3)如答图④所示,连接OC、OD.
∵△ABC为等腰三角形,点O为底边AB的中点,
∴=tan,∠BOC=90°.
∵△DEF为等腰三角形,点O为底边EF的中点,
∴=tan,∠DOF=90°.
∴==tan.
∵∠BOF=∠BOC+∠COF=90°+∠COF,∠COD=∠DOF+∠COF=90°+∠COF,
∴∠BOF=∠COD.
在△BOF与△COD中,
∵==tan,∠BOF=∠COD,
∴△BOF∽△COD,
∴=tan.
【点评】本题是几何综合题,考查了旋转变换中相似三角形、全等三角形的判定与性质.解题关键是:第一,善于发现几何变换中不变的逻辑关系,即△BOF≌△COD或△BOF∽△COD;第二,熟练运用等腰直角三角形、等边三角形、等腰三角形的相关性质.本题(1)(2)(3)问的解题思路一脉相承,由特殊到一般,有利于同学们进行学习与探究.
17.(2013•梅州)用如图①,②所示的两个直角三角形(部分边长及角的度数在图中已标出),完成以下两个探究问题:
探究一:将以上两个三角形如图③拼接(BC和ED重合),在BC边上有一动点P.
(1)当点P运动到∠CFB的角平分线上时,连接AP,求线段AP的长;
(2)当点P在运动的过程中出现PA=FC时,求∠PAB的度数.
探究二:如图④,将△DEF的顶点D放在△ABC的BC边上的中点处,并以点D为旋转中心旋转△DEF,使△DEF的两直角边与△ABC的两直角边分别交于M、N两点,连接MN.在旋转△DEF的过程中,△AMN的周长是否存在有最小值?若存在,求出它的最小值;若不存在,请说明理由.
【考点】几何变换综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)如答图1所示,过点A作AG⊥BC于点G,构造Rt△APG,利用勾股定理求出AP的长度;
(2)如答图2所示,符合条件的点P有两个.解直角三角形,利用特殊角的三角函数值求出角的度数;
(3)如答图3所示,证明△AMD≌△CND,得AM=CN,则△AMN两直角边长度之和为定值;设AM=x,求出斜边MN的表达式,利用二次函数的性质求出MN的最小值,从而得到△AMN周长的最小值.
【解答】解:探究一:(1)依题意画出图形,如答图1所示:
由题意,得∠CFB=60°,FP为角平分线,则∠CFP=30°,
∴CF=BC•tan30°=3×=,
∴CP=CF•tan∠CFP=×=1.
过点A作AG⊥BC于点G,则AG=BC=,
∴PG=CG﹣CP=﹣1=.
在Rt△APG中,由勾股定理得:
AP===.
(2)由(1)可知,FC=.
如答图2所示,以点A为圆心,以FC=长为半径画弧,与BC交于点P1、P2,则AP1=AP2=.
过点A过AG⊥BC于点G,则AG=BC=.
在Rt△AGP1中,cos∠P1AG===,
∴∠P1AG=30°,
∴∠P1AB=45°﹣30°=15°;
同理求得,∠P2AG=30°,∠P2AB=45°+30°=75°.
∴∠PAB的度数为15°或75°.
探究二:△AMN的周长存在有最小值.
如答图3所示,连接AD.
∵△ABC为等腰直角三角形,点D为斜边BC的中点,
∴AD=CD,∠C=∠MAD=45°.
∵∠EDF=90°,∠ADC=90°,
∴∠MDA=∠NDC.
∵在△AMD与△CND中,
∴△AMD≌△CND(ASA).
∴AM=CN.
设AM=x,则CN=x,AN=AC﹣CN=BC﹣CN=﹣x.
在Rt△AMN中,由勾股定理得:
MN====.
△AMN的周长为:AM+AN+MN=+,
当x=时,有最小值,最小值为+=.
∴△AMN周长的最小值为.
【点评】本题是几何综合题,考查了解直角三角形、勾股定理、全等三角形、二次函数最值等知识点.难点在于第(3)问,由发现并证明△AMD≌△CND取得解题的突破点,再利用勾股定理和二次函数的性质求出最小值.
18.(2015•营口)如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
(1)求证:PC是⊙O的切线;
(2)若PD=,AC=8,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是的中点,连接CE,求CE的长.
【考点】切线的判定;扇形面积的计算.菁优网版权所有
【专题】证明题.
【分析】(1)连接OC,证明△PAO≌△PCO,得到∠PCO=∠PAO=90°,证明结论;
(2)证明△ADP∽△PDA,得到成比例线段求出BC的长,根据S阴=S⊙O﹣S△ABC求出答案;
(3)连接AE、BE,作BM⊥CE于M,分别求出CM和EM的长,求和得到答案.
【解答】(1)证明:如图1,连接OC,
∵PA切⊙O于点A,∴∠PAO=90°,
∵BC∥OP,
∴∠AOP=∠OBC,∠COP=∠OCB,
∵OC=OB,∴∠OBC=∠OCB,
∴∠AOP=∠COP,
在△PAO和△PCO中,
,
∴△PAO≌△PCO,
∴∠PCO=∠PAO=90°,
∴PC是⊙O的切线;
(2)解:由(1)得PA,PC都为圆的切线,
∴PA=PC,OP平分∠APC,∠ADO=∠PAO=90°,
∴∠PAD+∠DAO=∠DAO+∠AOD,
∴∠PAD=∠AOD,
∴△ADP∽△ODA,
∴,
∴AD2=PD•DO,
∵AC=8,PD=,
∴AD=AC=4,OD=3,AO=5,
由题意知OD为△的中位线,
∴BC=6,OD=6,AB=10.
∴S阴=S⊙O﹣S△ABC=﹣24;
(3)解:如图2,连接AE、BE,作BM⊥CE于M,
∴∠CMB=∠EMB=∠AEB=90°,
∵点E是的中点,
∴∠ECB=∠CBM=∠ABE=45°,
CM=MB=3,
BE=AB•cos45°=5,
∴EM==4,
则CE=CM+EM=7.
【点评】本题考查的是切线的判定和性质、扇形面积的计算和相似三角形的判定和性质,灵活运用切线的性质:圆的切线垂直于过切点的半径和切线的判定是解题的关键.
19.(2015•永州)问题探究:
(一)新知学习:
圆内接四边形的判断定理:如果四边形对角互补,那么这个四边形内接于圆(即如果四边形EFGH的对角互补,那么四边形EFGH的四个顶点E、F、G、H都在同个圆上).
(二)问题解决:
已知⊙O的半径为2,AB,CD是⊙O的直径.P是上任意一点,过点P分别作AB,CD的垂线,垂足分别为N,M.
(1)若直径AB⊥CD,对于上任意一点P(不与B、C重合)(如图一),证明四边形PMON内接于圆,并求此圆直径的长;
(2)若直径AB⊥CD,在点P(不与B、C重合)从B运动到C的过程中,证明MN的长为定值,并求其定值;
(3)若直径AB与CD相交成120°角.
①当点P运动到的中点P1时(如图二),求MN的长;
②当点P(不与B、C重合)从B运动到C的过程中(如图三),证明MN的长为定值.
(4)试问当直径AB与CD相交成多少度角时,MN的长取最大值,并写出其最大值.
【考点】圆的综合题.菁优网版权所有
【专题】压轴题;探究型.
【分析】(1)如图一,易证∠PMO+∠PNO=180°,从而可得四边形PMON内接于圆,直径OP=2;
(2)如图一,易证四边形PMON是矩形,则有MN=OP=2,问题得以解决;
(3)①如图二,根据等弧所对的圆心角相等可得∠COP1=∠BOP1=60°,根据圆内接四边形的对角互补可得∠MP1N=60°.根据角平分线的性质可得P1M=P1N,从而得到△P1MN是等边三角形,则有MN=P1M.然后在Rt△P1MO运用三角函数就可解决问题;②设四边形PMON的外接圆为⊙O′,连接NO′并延长,交⊙O′于点Q,连接QM,如图三,根据圆周角定理可得∠QMN=90°,∠MQN=∠MPN=60°,在Rt△QMN中运用三角函数可得:MN=QN•sin∠MQN,从而可得MN=OP•sin∠MQN,由此即可解决问题;
(4)由(3)②中已得结论MN=OP•sin∠MQN可知,当∠MQN=90°时,MN最大,问题得以解决.
【解答】解:(1)如图一,
∵PM⊥OC,PN⊥OB,
∴∠PMO=∠PNO=90°,
∴∠PMO+∠PNO=180°,
∴四边形PMON内接于圆,直径OP=2;
(2)如图一,
∵AB⊥OC,即∠BOC=90°,
∴∠BOC=∠PMO=∠PNO=90°,
∴四边形PMON是矩形,
∴MN=OP=2,
∴MN的长为定值,该定值为2;
(3)①如图二,
∵P1是的中点,∠BOC=120°
∴∠COP1=∠BOP1=60°,∠MP1N=60°.
∵P1M⊥OC,P1N⊥OB,
∴P1M=P1N,
∴△P1MN是等边三角形,
∴MN=P1M.
∵P1M=OP1•sin∠MOP1=2×sin60°=,
∴MN=;
②设四边形PMON的外接圆为⊙O′,连接NO′并延长,
交⊙O′于点Q,连接QM,如图三,
则有∠QMN=90°,∠MQN=∠MPN=60°,
在Rt△QMN中,sin∠MQN=,
∴MN=QN•sin∠MQN,
∴MN=OP•sin∠MQN=2×sin60°=2×=,
∴MN是定值.
(4)由(3)②得MN=OP•sin∠MQN=2sin∠MQN.
当直径AB与CD相交成90°角时,∠MQN=180°﹣90°=90°,MN取得最大值2.
【点评】本题主要考查了圆内接四边形的判定定理、圆周角定理、在同圆中弧与圆心角的关系、矩形的判定与性质、等边三角形的判定与性质、三角函数、角平分线的性质等知识,推出MN=OP•sin∠MQN是解决本题的关键.
20.(2015•盘锦)如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
(1)请直接写出线段BE与线段CD的关系: BE=CD ;
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0<α<360°),
①(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请说明理由;
②当AC=ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
【考点】几何变换综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)根据等腰直角三角形的性质可得AB=AC,AE=AD,再根据等量关系可得线段BE与线段CD的关系;
(2)①根据等腰直角三角形的性质可得AB=AC,AE=AD,根据旋转的性质可得∠BAE=∠CAD,根据SAS可证△BAE≌△CAD,根据全等三角形的性质即可求解;
②根据平行四边形的性质可得∠ABC=∠ADC=45°,再根据等腰直角三角形的性质即可求解.
【解答】解:(1)∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD,
∴AE﹣AB=AD﹣AC,
∴BE=CD;
(2)①∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD,
由旋转的性质可得∠BAE=∠CAD,
在△BAE与△CAD中,
,
∴△BAE≌△CAD(SAS)
∴BE=CD;
②∵以A、B、C、D四点为顶点的四边形是平行四边形,△ABC和△AED都是等腰直角三角形,
∴∠ABC=∠ADC=45°,
∵AC=ED,
∴AC=CD,
∴∠CAD=45°
或360°﹣90°﹣45°=225°,或360°﹣45°=315°
∴角α的度数是45°或225°或315°.
故答案为:BE=CD.
【点评】考查了几何变换综合题,涉及的知识点有:等腰直角三角形的性质,等量代换,旋转的性质,全等三角形的判定和性质,平行四边形的判定和性质,综合性较强,难度中等.
21.(2015•朝阳)问题:如图(1),在Rt△ACB中,∠ACB=90°,AC=CB,∠DCE=45°,试探究AD、DE、EB满足的等量关系.
[探究发现]
小聪同学利用图形变换,将△CAD绕点C逆时针旋转90°得到△CBH,连接EH,由已知条件易得∠EBH=90°,∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°.
根据“边角边”,可证△CEH≌ △CDE ,得EH=ED.
在Rt△HBE中,由 勾股 定理,可得BH2+EB2=EH2,由BH=AD,可得AD、DE、EB之间的等量关系是 AD2+EB2=DE2 .
[实践运用]
(1)如图(2),在正方形ABCD中,△AEF的顶点E、F分别在BC、CD边上,高AG与正方形的边长相等,求∠EAF的度数;
(2)在(1)条件下,连接BD,分别交AE、AF于点M、N,若BE=2,DF=3,BM=2,运用小聪同学探究的结论,求正方形的边长及MN的长.
【考点】几何变换综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)根据正方形的性质和全等三角形的判定方法证明Rt△ABE≌Rt△AGE和Rt△ADF≌Rt△AGF,由全等三角形的性质即可求出∠EAF=∠BAD=45°;
(2)由(1)知,Rt△ABE≌Rt△AGE,Rt△ADF≌Rt△AGF,设AG=x,则CE=x﹣2,CF=x﹣3.因为CE2+CF2=EF2,所以(x﹣2)2+(x﹣3)2=52.解这个方程,求出x的值即可得到AG=6,在(2)中,MN2=MB2+ND2,MN=a,,所以a=.即MN=.
【解答】解:根据“边角边”,可证△CEH≌△CDE,得EH=ED.
在Rt△HBE中,由勾股定理,可得BH2+EB2=EH2,由BH=AD,可得AD、DE、EB之间的等量关系是AD2+EB2=DE2;故答案为:△CDE;勾股;AD2+EB2=DE2;
(1)在Rt△ABE和Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴∠BAE=∠GAE,
同理,Rt△ADF≌Rt△AGF,
∴∠GAF=∠DAF,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠EAF=∠BAD=45°;
(2)由(1)知,Rt△ABE≌Rt△AGE,Rt△ADF≌Rt△AGF,
∴BE=EG=2,DF=FG=3,则EF=5,
设AG=x,则CE=x﹣2,CF=x﹣3,
∵CE2+CF2=EF2,
∴(x﹣2)2+(x﹣3)2=52,
解这个方程,得x1=6,x2=﹣1(舍去),
∴AG=6,
∴BD=,
∴AB=6,
∵MN2=MB2+ND2
设MN=a,则,
所以a=,
即MN=.
【点评】本题考查了正方形的性质、直角三角形的性质、全等三角形的判定和性质以及勾股定理的运用和一元二次方程的运用,题目的综合性很强,难度不小.
22.(2015•自贡)在△ABC中,AB=AC=5,cos∠ABC=,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1,求线段EF1长度的最大值与最小值的差.
【考点】几何变换综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)①根据旋转的性质和平行线的性质证明;
②过A作AF⊥BC于F,过C作CE⊥AB于E,根据三角函数和三角形的面积公式解答;
(2)过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,和以C为圆心BC为半径画圆交BC的延长线于F1,得出最大和最小值解答即可.
【解答】解:(1)①证明:∵AB=AC,B1C=BC,
∴∠AB1C=∠B,∠B=∠ACB,
∵∠AB1C=∠ACB(旋转角相等),
∴∠B1CA1=∠AB1C,
∴BB1∥CA1;
②过A作AF⊥BC于F,过C作CE⊥AB于E,如图①:
∵AB=AC,AF⊥BC,
∴BF=CF,
∵cos∠ABC=,AB=5,
∴BF=3,
∴BC=6,
∴B1C=BC=6,
∵CE⊥AB,
∴BE=B1E=,
∴BB1=,CE=,
∴AB1=,
∴△AB1C的面积为:;
(2)如图2,过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,EF1有最小值,
此时在Rt△BFC中,CF=,
∴CF1=,
∴EF1的最小值为;
如图,以C为圆心BC为半径画圆交BC的延长线于F1,EF1有最大值;
此时EF1=EC+CF1=3+6=9,
∴线段EF1的最大值与最小值的差为.
【点评】此题考查几何变换问题,关键是根据旋转的性质和三角形的面积公式进行解答.
23.(2015•吉林)两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).
(1)当点C落在边EF上时,x= 15 cm;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,点M与点N之间距离的最小值.
【考点】几何变换综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)根据锐角三角函数,可得BG的长,根据线段的和差,可得GE的长,根据矩形的性质,可得答案;
(2)分类讨论:①当0≤t<6时,根据三角形的面积公式,可得答案;②当6≤t<12时,③当12<t≤15时,根据面积的和差,可得答案;
(3)根据点与直线上所有点的连线中垂线段最短,可得M在线段NG上,根据三角形的中位线,可得NG的长,根据锐角三角函数,可得MG的长,根据线段的和差,可得答案.
【解答】解:(1)如图1所示:作CG⊥AB于G点.,
在Rt△ABC中,由AC=6,∠ABC=30,得
BC==6.
在Rt△BCG中,BG=BC•cos30°=9.
四边形CGEH是矩形,
CH=GE=BG+BE=9+6=15cm,
故答案为:15;
(2)①当0≤x<6时,如图2所示.,
∠GDB=60°,∠GBD=30°,DB=x,得
DG=x,BG=x,重叠部分的面积为y=DG•BG=×x×x=x2
②当6≤x<12时,如图3所示.,
BD=x,DG=x,BG=x,BE=x﹣6,EH=(x﹣6).
重叠部分的面积为y=S△BDG﹣S△BEH=DG•BG﹣BE•EH,
即y=×x×x﹣(x﹣6)(x﹣6)
化简,得y=﹣x2+2x﹣6;
③当12<x≤15时,如图4所示.,
AC=6,BC=6,BD=x,BE=(x﹣6),EG=(x﹣6),
重叠部分的面积为y=S△ABC﹣S△BEG=AC•BC﹣BE•EG,
即y=×6×6﹣(x﹣6)(x﹣6),
化简,得y=18﹣(x2﹣12x+36)=﹣x2+2x+12;
综上所述:y=;
(3)如图5所示作NG⊥DE于G点.,
点M在NG上时MN最短,
NG是△DEF的中位线,
NG=EF=.
MB=CB=3,∠B=30°,
MG=MB=,
MN最小=3﹣=.
【点评】本题考查了几何变换综合题,(1)利用了锐角三角函数,矩形的性质;(2)利用面积的和差,分类讨论时解题关键,以防遗漏;(3)利用了垂线段最短的性质,三角形的中位线定理,锐角三角函数.
24.(2015•汕尾)在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是边AB,AC的中点,若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)如图1,当α=90°时,线段BD1的长等于 2 ,线段CE1的长等于 2 ;(直接填写结果)
(2)如图2,当α=135°时,求证:BD1=CE1,且BD1⊥CE1;
(3)求点P到AB所在直线的距离的最大值.(直接写出结果)
【考点】几何变换综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)利用等腰直角三角形的性质结合勾股定理分别得出BD1的长和CE1的长;
(2)根据旋转的性质得出,∠D1AB=∠E1AC=135°,进而求出△D1AB≌△E1AC(SAS),即可得出答案;
(3)首先作PG⊥AB,交AB所在直线于点G,则D1,E1在以A为圆心,AD为半径的圆上,当BD1所在直线与⊙A相切时,直线BD1与CE1的交点P到直线AB的距离最大,
此时四边形AD1PE1是正方形,进而求出PG的长.
【解答】(1)解:∵∠A=90°,AC=AB=4,D,E分别是边AB,AC的中点,
∴AE=AD=2,
∵等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,设旋转角为α(0<α≤180°),
∴当α=90°时,AE1=2,∠E1AE=90°,
∴BD1==2,E1C==2;
故答案为:2,2;
(2)证明:当α=135°时,如图2,
∵Rt△AD1E是由Rt△ADE绕点A逆时针旋转135°得到,
∴AD1=AE1,∠D1AB=∠E1AC=135°,
在△D1AB和△E1AC中
∵,
∴△D1AB≌△E1AC(SAS),
∴BD1=CE1,且∠D1BA=∠E1CA,
记直线BD1与AC交于点F,
∴∠BFA=∠CFP,
∴∠CPF=∠FAB=90°,
∴BD1⊥CE1;
(3)解:如图3,作PG⊥AB,交AB所在直线于点G,
∵D1,E1在以A为圆心,AD为半径的圆上,
当BD1所在直线与⊙A相切时,直线BD1与CE1的交点P到直线AB的距离最大,
此时四边形AD1PE1是正方形,PD1=2,则BD1==2,
故∠ABP=30°,
则PB=2+2,
故点P到AB所在直线的距离的最大值为:PG=1+.
【点评】此题主要考查了几何变换以及等腰腰直角三角形的性质和勾股定理以及切线的性质等知识,根据题意得出PG的最长时P点的位置是解题关键.
25.(2015•赤峰)如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?
【考点】几何变换综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)如答图1,连接BD.根据题干条件首先证明∠ADF=∠BDE,然后证明△ADF≌△BDE(ASA),得DF=DE;
(2)如答图2,连接BD.根据题干条件首先证明∠ADF=∠BDE,然后证明△ADF≌△BDE(ASA),得DF=DE;
(3)根据(2)中的△ADF≌△BDE得到:S△ADF=S△BDE,AF=BE.所以△DEF的面积转化为:y=S△BEF+S△ABD.据此列出y关于x的二次函数,通过求二次函数的最值来求y的最小值.
【解答】解:(1)DF=DE.理由如下:
如答图1,连接BD.
∵四边形ABCD是菱形,
∴AD=AB.
又∵∠DAB=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠DAF=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.∵在△ADF与△BDE中,,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(2)DF=DE.理由如下:
如答图2,连接BD.∵四边形ABCD是菱形,
∴AD=AB.
又∵∠DAB=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠DAF=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.
∵在△ADF与△BDE中,,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(3)由(2)知,DE=DF,又∵∠EDF=60°,
∴△DEF是等边三角形,
∵四边形ABCD是边长为2的菱形,
∴DH=,
∵BF=CE=x,
∴AF=x﹣2,
∴FH=AF+AH=x﹣2+1=x﹣1,
∴DF==,DG=×,
∴y=S△DEF=×EF×DG=×××=(x﹣1)2+.
∴当x=1时,y最小值=.
【点评】本题考查了几何变换综合题,解题过程中,利用了三角形全等的判定与性质,菱形的性质以及等边三角形的判定与性质,对于促进角与角(边与边)相互转换,将未知角转化为已知角(未知边转化为已知边)是关键.
26.(2015•海南)如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点.
(1)求证:△ADP≌△ECP;
(2)若BP=n•PK,试求出n的值;
(3)作BM丄AE于点M,作KN丄AE于点N,连结MO、NO,如图2所示,请证明△MON是等腰三角形,并直接写出∠MON的度数.
【考点】四边形综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)根据菱形的性质得到AD∥BC,根据平行线的性质得到对应角相等,根据全等三角形的判定定理证明结论;
(2)作PI∥CE交DE于I,根据点P是CD的中点证明CE=2PI,BE=4PI,根据相似三角形的性质证明结论;
(3)作OG⊥AE于G,根据平行线等分线段定理得到MG=NG,又OG⊥MN,证明△MON是等腰三角形,根据直角三角形的性质和锐角三角函数求出∠MON的度数.
【解答】(1)证明:∵四边形ABCD为菱形,
∴AD∥BC,
∴∠DAP=∠CEP,∠ADP=∠ECP,
在△ADP和△ECP中,
,
∴△ADP≌△ECP;
(2)如图1,作PI∥CE交DE于I,
则=,又点P是CD的中点,
∴=,
∵△ADP≌△ECP,
∴AD=CE,
∴==,
∴BP=3PK,
∴n=3;
(3)如图2,作OG⊥AE于G,
∵BM丄AE于M,KN丄AE于N,
∴BM∥OG∥KN,
∵点O是线段BK的中点,
∴MG=NG,又OG⊥MN,
∴OM=ON,
即△MON是等腰三角形,
由题意得,△BPC,△AMB,△ABP为直角三角形,
设BC=2,则CP=1,由勾股定理得,BP=,
则AP=,
根据三角形面积公式,BM=,
由(2)得,PB=3PO,
∴OG=BM=,
MG=MP=,
tan∠MOG==,
∴∠MOG=60°,
∴∠MON的度数为120°.
【点评】本题考查的是菱形的性质和相似三角形的判定和性质、全等三角形的判定和性质,灵活运用判定定理和性质定理是解题的关键,注意锐角三角函数在解题中的运用.
27.(2015•丹东)在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.
(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=m•BP时,请直接写出PE与PF的数量关系.
【考点】四边形综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)根据正方形的性质和角平分线的性质解答即可;
(2)①根据正方形的性质和旋转的性质证明△FOA≌△EOD,得到答案;
②作OG⊥AB于G,根据余弦的概念求出OF的长,根据勾股定理求值即可;
③过点P作HP⊥BD交AB于点H,根据相似三角形的判定和性质求出PE与PF的数量关系,根据解答结果总结规律得到当BD=m•BP时,PE与PF的数量关系.
【解答】解:(1)PE=PF,理由:
∵四边形ABCD为正方形,
∴∠BAC=∠DAC,又PM⊥AD、PN⊥AB,
∴PE=PF;
(2)①成立,理由:
∵AC、BD是正方形ABCD的对角线,
∴OA=OD,∠FAO=∠EDO=45°,∠AOD=90°,
∴∠DOE+∠AOE=90°,
∵∠MPN=90°,
∴∠FOA+∠AOE=90°,
∴∠FOA=∠DOE,
在△FOA和△EOD中,
,
∴△FOA≌△EOD,
∴OE=OF,即PE=PF;
②作OG⊥AB于G,
∵∠DOM=15°,
∴∠AOF=15°,则∠FOG=30°,
∵cos∠FOG=,
∴OF==,又OE=OF,
∴EF=;
③PE=2PF,
证明:如图3,过点P作HP⊥BD交AB于点H,
则△HPB为等腰直角三角形,∠HPD=90°,
∴HP=BP,
∵BD=3BP,
∴PD=2BP,
∴PD=2 HP,
又∵∠HPF+∠HPE=90°,∠DPE+∠HPE=90°,
∴∠HPF=∠DPE,
又∵∠BHP=∠EDP=45°,
∴△PHF∽△PDE,
∴==,
即PE=2PF,
由此规律可知,当BD=m•BP时,PE=(m﹣1)•PF.
【点评】本题考查的是正方形的性质和旋转变换,掌握旋转变换的性质、找准对应关系正确运用三角形全等和相似的判定和性质定理是解题的关键,正确作出辅助线是解答本题的重点.
28.(2015•成都)已知AC,EC分别是四边形ABCD和EFDC的对角线,点E在△ABC内,∠CAE+∠CBE=90°.
(1)如图①,当四边形ABCD和EFCG均为正方形时,连接BF.
(i)求证:△CAE∽△CBF;
(ii)若BE=1,AE=2,求CE的长;
(2)如图②,当四边形ABCD和EFCG均为矩形,且==k时,若BE=1,AE=2,CE=3,求k的值;
(3)如图③,当四边形ABCD和EFCG均为菱形,且∠DAB=∠GEF=45°时,设BE=m,AE=n,CE=p,试探究m,n,p三者之间满足的等量关系.(直接写出结果,不必写出解答过程)
【考点】四边形综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)(i)首先根据四边形ABCD和EFCG均为正方形,可得,∠ACE=∠BCF;然后根据相似三角形判定的方法,推得△CAE∽△CBF即可.
(ii)首先根据△CAE∽△CBF,判断出∠CAE=∠△CBF,再根据∠CAE+∠CBE=90°,判断出∠EBF=90°;然后在Rt△BEF中,根据勾股定理,求出EF的长度,再根据CE、EF的关系,求出CE的长是多少即可.
(2)首先根据相似三角形判定的方法,判断出△ACE∽△∠BCF,即可判断出,据此求出BF的长度是多少;然后判断出∠EBF=90°,在Rt△BEF中,根据勾股定理,求出EF的值是多少,进而求出k的值是多少即可.
(3)首先根据∠DAB=45°,可得∠ABC=180°﹣45°=135°,在△ABC中,根据勾股定理可求得AB2、BC2,AC2之间的关系,EF2、FC2,EC2之间的关系;然后根据相似三角形判定的方法,判断出△ACE∽△∠BCF,即可用n表示出BF的值;最后判断出EBF=90°,在Rt△BEF中,根据勾股定理,判断出m,n,p三者之间满足的等量关系即可.
【解答】(1)(i)证明:∵四边形ABCD和EFCG均为正方形,
∴,
∴∠ACB=∠ECF=45°,
∴∠ACE=∠BCF,
在△CAE和△CBF中,
,
∴△CAE∽△CBF.
(ii)解:∵△CAE∽△CBF,
∴∠CAE=∠△CBF,,
又∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
又∵,AE=2
∴,
∴,
∴EF2=BE2+BF2==3,
∴EF=,
∵CE2=2EF2=6,
∴CE=.
(2)如图②,连接BF,
∵==k,
∴BC=a,AB=ka,FC=b,EF=kb,
∴AC=,
CE==,
∴,∠ACE=∠BCF,
在△ACE和△∠BCF中,
,
∴△ACE∽△∠BCF,
∴,∠CAE=∠CBF,
又∵AE=2,
∴,
∴BF=,
∵∠CAE=∠CBF,∠CAE+∠CBE=90°,
∴∠CBE+∠CBF=90°,
∴∠EBF=90°,
∴EF2=BE2+BF2=1,
∵,
∴=,CE=3,
∴EF=,
∴1,
∴,
解得k=±,
∵==k>0,
∴k=.
(3)(3)连结BF,同理可得∠EBF=90°,过C点作CH⊥AB延长线于H,
∵四边形ABCD为菱形,
∴AB=BC,设AB=BC=x,
∵∠CBH=∠DAB=45°,∴BH=CH=x,
∴AC2=AH2+CH2=(x+x)2+(x)2,=(2+)x2,
∴AB2:BC2:AC2=1:1:(2+),
同理可得EF2:FC2:EC2=1:1:(2+),
∴EF2==,
在△ACE和△∠BCF中,
,
∴△ACE∽△∠BCF,
∴==2+,∠CAE=∠CBF,
又∵AE=n,
∴,
∵∠CAE=∠CBF,∠CAE+∠CBE=90°,
∴∠CBE+∠CBF=90°,
∴∠EBF=90°,
∴EF2=BE2+BF2,
∴,
∴(2)m2+n2=p2,
即m,n,p三者之间满足的等量关系是:(2)m2+n2=p2.
【点评】(1)此题主要考查了四边形综合题,考查了分析推理能力,考查了空间想象能力,考查了数形结合方法的应用,要熟练掌握.
(2)此题还考查了相似三角形的判定和性质的应用,要熟练掌握.
(3)此题还考查了直角三角形的性质和应用,以及勾股定理的应用,要熟练掌握.
29.(2015•锦州)如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是 DE+DF=AD ;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=AD,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
【考点】四边形综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)利用正方形的性质得出角与线段的关系,易证得△APE≌△DPF,可得出AE=DF,即可得出结论DE+DF=AD,
(2)取AD的中点M,连接PM,利用菱形的性质,可得出△MDP是等边三角形,易证△MPE≌△FPD,得出ME=DF,由DE+ME=AD,即可得出DE+DF=AD,
(3)①当点E落在AD上时,DE+DF=AD,②当点E落在AD的延长线上时,DF﹣DE=AD.
【解答】解:(1)正方形ABCD的对角线AC,BD交于点P,
∴PA=PD,∠PAE=∠PDF=45°,
∵∠APE+∠EPD=∠DPF+∠EPD=90°,
∴∠APE=∠DPF,
在△APE和△DPF中
∴△APE≌△DPF(ASA),
∴AE=DF,
∴DE+DF=AD;
(2)如图②,取AD的中点M,连接PM,
∵四边形ABCD为∠ADC=120°的菱形,
∴BD=AD,∠DAP=30°,∠ADP=∠CDP=60°,
∴△MDP是等边三角形,
∴PM=PD,∠PME=∠PDF=60°,
∵∠PAM=30°,
∴∠MPD=60°,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△MPE和△DPF中,
∴△MPE≌△DPF(ASA)
∴ME=DF,
∴DE+DF=AD;
(3)如图,
在整个运动变化过程中,
①当点E落在AD上时,DE+DF=AD;
②当点E落在AD的延长线上时,DF﹣DE=AD.
(如图3,取AD中点M,连接PM,证明△MPE≌△DPF)
【点评】本题主要考查了四边形的综合题,涉及全等三角形,正方形及菱形的性质,解答本题的关键是设计三角形全等,巧妙地借助两个三角形全等,寻找所求线段与线段之间的等量关系.
30.(2014•绵阳)如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.
【考点】四边形综合题.菁优网版权所有
【专题】压轴题.
【分析】(1)由矩形和翻折的性质可知AD=CE,DC=EA,根据“SSS”可求得△DEC≌△EDA;
(2)根据勾股定理即可求得.
(3)由矩形PQMN的性质得PQ∥CA,所以,从而求得PQ,由PN∥EG,得出=,求得PN,然后根据矩形的面积公式求得解析式,即可求得.
【解答】(1)证明:由矩形和翻折的性质可知:AD=CE,DC=EA,
在△ADE与△CED中,
∴△DEC≌△EDA(SSS);
(2)解:如图1,
∵∠ACD=∠BAC,∠BAC=∠CAE,
∴∠ACD=∠CAE,
∴AF=CF,
设DF=x,则AF=CF=4﹣x,
在Rt△ADF中,AD2+DF2=AF2,
即32+x2=(4﹣x)2,
解得:x=,
即DF=.
(3)解:如图2,由矩形PQMN的性质得PQ∥CA
∴
又∵CE=3,AC==5
设PE=x(0<x<3),则,即PQ=
过E作EG⊥AC于G,则PN∥EG,
∴=
又∵在Rt△AEC中,EG•AC=AE•CE,解得EG=,
∴=,即PN=(3﹣x),
设矩形PQMN的面积为S,
则S=PQ•PN=﹣x2+4x=﹣+3(0<x<3)
所以当x=,即PE=时,矩形PQMN的面积最大,最大面积为3.
【点评】本题考查了全等三角形的判定和性质,勾股定理的应用,平行线分线段成比例定理.