深圳中考数学试题与答案word版 9页

绝 密 ‎2009年深圳市初中毕业生学业考试数学试卷 说明：‎ ‎1.全卷分二部分，第一部分为选择题，第二部分为非选择题，共 4页。考试时间90分钟，满分100分。‎ ‎2.考生必须在答题卡上按规定作答；答题卡必须保持清洁，不能折叠。‎ ‎3.答题前，请将姓名、考生号、考场等用规定的笔填涂在答题卡指定的位置上。‎ ‎4.本卷选择题1—10，每小题选出答案后，用2B铅笔将答题卡选择题答题区内对应题目的答案标号涂黑；非选择题11—22，答案（含作辅助线）必须用规定的笔，按作答题目序号，写在答题卡非选择题答题区内相应位置上，写在本卷或其他地方无效。‎ 第一部分 选择题 一、选择题（本题有10小题，每题3分，共30分）‎ ‎1．如果a的倒数是1，那么a2009等于（ ）‎ A．1 B．1 ‎ C．2009 D．2009‎ ‎2．由若干个相同的小立方体搭成的几何体的三视图如图所示，则搭成这个几何体的小立方体的个数是（ ）‎ A．3 B．4 C．5 D．6‎ ‎ 主视图 左视图 俯视图 ‎3．用配方法将代数式a2+4a-5变形，结果正确的是（ ）‎ A.(a+2)2-1 B. (a+2)2-5 ‎ C. (a+2)2+4 D. (a+2)2-9‎ ‎4．横跨深圳及香港之间的深圳湾大桥（Shenzhen Bay Bridge）是中国唯一倾斜的独塔单索面桥，大桥全长4770米，这个数字用科学计数法表示为（保留两个有效数字）（ ）‎ A． B． ‎ C． D．‎ ‎5．下面的图形中，既是轴对称图形又是中心对称图形的是（ ）‎ A． B． C． D．‎ ‎6．下图是同一副扑克中的4张扑克牌的正面，将它们正面朝下洗匀后放在桌上，小明从中抽出一张，则抽到偶数的概率是（ ）‎ A O B C A． B． C． D．‎ ‎7．如图，反比例函数的图象与直线的交点 为A，B，过点A作y轴的平行线与过点B作x轴的平 行线相交于点C，则的面积为（　　）‎ A．8 ‎ B．6 ‎ C．4 ‎ D．2‎ ‎8．如图，数轴上与1，对应的点分别为A，B，点B关于点A的对称点为C，设点C表示的数为x，则（　　）‎ O C A B x ‎1‎ A． B． ‎ C． D．2‎ ‎9．某商场的老板销售一种商品，他要以不低于进价20%价格才能出售，但为了获得更多利润，他以高出进价80%的价格标价．若你想买下标价为360元的这种商品，最多降价多少时商店老板才能出售（　　）‎ A．80元 B．100元 ‎ C．120元 D．160元 A D C B ‎10．如图，已知点A、B、C、D均在已知圆上，AD//BC，AC平分，，四边形ABCD的周长为10cm．图中阴影部分的面积为（ ）‎ ‎ A. B. ‎ C. D. 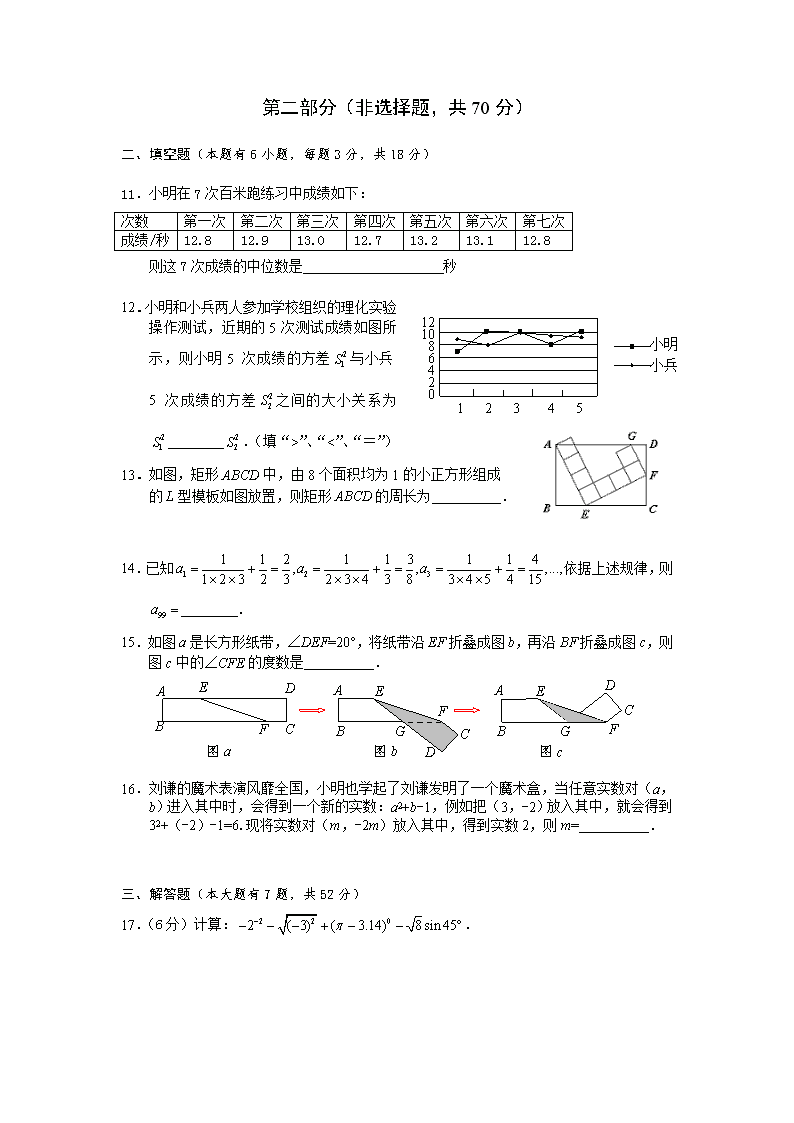‎ 第二部分（非选择题，共70分）‎ 二、填空题（本题有6小题，每题3分，共18分）‎ ‎11．小明在7次百米跑练习中成绩如下：‎ 次数 第一次 第二次 第三次 第四次 第五次 第六次 第七次 成绩/秒 ‎12.8‎ ‎12.9‎ ‎13.0‎ ‎12.7‎ ‎13.2‎ ‎13.1‎ ‎12.8‎ 则这7次成绩的中位数是 秒 ‎ ‎12‎ ‎10‎ ‎8‎ ‎6‎ ‎4‎ ‎2‎ ‎0‎ ‎1 2 3 4 5‎ 小明 小兵 ‎12．小明和小兵两人参加学校组织的理化实验操作测试，近期的5次测试成绩如图所示，则小明5次成绩的方差与小兵5次成绩的方差之间的大小关系为　　　　．（填“>”、“<”、“＝”）‎ ‎13．如图，矩形ABCD中，由8个面积均为1的小正方形组成 的L型模板如图放置，则矩形ABCD的周长为 _．‎ ‎14．已知依据上述规律，则 ． ‎ A DA C BA EA CA BA FA DA C DBA EA FCA GBA A BA EA FCA GBA A 图a 图b 图c ‎15．如图a是长方形纸带，∠DEF=20°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是 ．‎ ‎16．刘谦的魔术表演风靡全国，小明也学起了刘谦发明了一个魔术盒，当任意实数对（a，b）进入其中时，会得到一个新的实数：a2+b-1，例如把（3，-2）放入其中，就会得到 ‎32+（-2）-1=6.现将实数对（m，-2m）放入其中，得到实数2，则m= ．‎ 三、解答题（本大题有7题，共52分）‎ ‎17．（6分）计算：．‎ ‎18．（6分）先阅读理解下面的例题，再按要求解答：‎ 例题：解一元二次不等式.‎ 解：∵，‎ ‎∴.‎ 由有理数的乘法法则“两数相乘，同号得正”，有 ‎（1） （2）‎ 解不等式组（1），得，‎ 解不等式组（2），得，‎ 故的解集为或，‎ 即一元二次不等式的解集为或.‎ ‎ 问题：求分式不等式的解集.‎ A B C D ‎19．（6分）如图，斜坡AC的坡度（坡比）为1:，AC＝10米．坡顶有一旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB＝14米．‎ 试求旗杆BC的高度． ‎ ‎20．（7分）深圳大学青年志愿者协会对报名参加2011年深圳大运会志愿者选拔活动的学生进行了一次与大运知识有关的测试，小亮对自己班有报名参加测试的同学的测试成绩作了适当的处理，将成绩分成三个等级:一般、良好、优秀，并将统计结果绘成了如下两幅不完整的统计图，请你根据图中所给信息解答下列问题：‎ ‎（1）请将两幅统计图补充完整；‎ ‎（2）小亮班共有 名学生参加了这次测试，如果青年志愿者协会决定让成绩为“优秀”的学生参加下一轮的测试,那么小亮班有 人将参加下轮测试；‎ ‎（3）若这所高校共有1200名学生报名参加了这次志愿者选拔活动的测试，请以小亮班的测试成绩的统计结果来估算全校共有多少名学生可以参加下一轮的测试。‎ ‎21．（8分）迎接大运，美化深圳，园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在迎宾大道两侧，已知搭配一个A种造型需甲种花卉80盆，乙种花卉40盆，搭配一个B种造型需甲种花卉50盆，乙种花卉90盆．‎ ‎（1）某校九年级（1）班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来．‎ ‎（2）若搭配一个A种造型的成本是800元，搭配一个B种造型的成本是960元，试说明（1）中哪种方案成本最低？最低成本是多少元？‎ ‎22．（9分）如图，在直角坐标系中，点A的坐标为（－2，0），连结OA，将线段OA绕原点O顺时针旋转120°，得到线段OB.‎ ‎（1）求点B的坐标；‎ ‎（2）求经过A、O、B三点的抛物线的解析式；‎ ‎（3）在（2）中抛物线的对称轴上是否存在点C，使△BOC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由.‎ ‎（4）如果点P是（2）中的抛物线上的动点，且在x轴的下方，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由.‎ B A O y x ‎23．如图，在平面直角坐标系中，直线l：y=－2x－8分别与x轴，y轴相交于A，B两点，点P（0，k）是y轴的负半轴上的一个动点，以P为圆心，3为半径作⊙P.‎ ‎（1）连结PA，若PA=PB，试判断⊙P与x轴的位置关系，并说明理由；‎ ‎（2）当k为何值时，以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形？‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 参考答案：‎ 一、选择题 ‎1. B；2. B ；3. D；4. C；5. C；6. C ；7. A；8. C；9. C ；10. B ；‎ 二、填空题 ‎11. 12.9；12. ＜；13. ；14. ；15. 120° ；16. 3或－1；‎ 三、解答题 ‎17. ．‎ ‎18. 解：由有理数的除法法则“两数相除，同号得正”，有 ‎（1） （2）‎ 解不等式组（1），得，解不等式组（2），得无解，‎ 故分式不等式的解集为.‎ ‎19. 解：延长BC交AD于E点，则CE⊥AD．‎ A B C D E 在Rt△AEC中，AC＝10， 由坡比为1︰可知：∠CAE＝30°，‎ ‎∴ CE＝AC·sin30°＝10×＝5，‎ AE＝AC·cos30°＝10×＝ ．‎ 在Rt△ABE中，BE＝＝＝11．‎ ‎∵ BE＝BC＋CE，∴ BC＝BE－CE＝11-5＝6（米）． ‎ 答：旗杆的高度为6米．‎ ‎20. 解：（1）略；（2）40，20；（3）600．‎ ‎21. 解：设搭配A种造型x个，则B种造型为个，‎ 依题意，得：解得：，∴‎ ‎∵x是整数，x可取31、32、33，‎ ‎∴可设计三种搭配方案：①A种园艺造型31个，B种园艺造型19个；②A种园艺造型32个，B种园艺造型18个；③A种园艺造型33个，B种园艺造型17个．‎ ‎（2）方法一：由于B种造型的造价成本高于A种造型成本．所以B种造型越少，成本越低，故应选择方案③，成本最低，最低成本为：33×800+17×960=42720（元）‎ 方法二：方案①需成本：31×800+19×960=43040（元）；‎ 方案②需成本：32×800+18×960=42880（元）；‎ 方案③需成本：33×800+17×960=42720（元）；‎ ‎∴应选择方案③，成本最低，最低成本为42720元．‎ ‎22. 解：（1）B（1，）‎ ‎（2）设抛物线的解析式为y=ax(x+a)，代入点B（1, ），得，‎ 因此 ‎（3）如图，抛物线的对称轴是直线x=—1，当点C位于对称轴与线段AB的交点时，△BOC的周长最小.‎ C B A O y x 设直线AB为y=kx+b.所以，‎ 因此直线AB为，‎ 当x=－1时，，‎ 因此点C的坐标为（－1，）.‎ D B A O y x P ‎（4）如图，过P作y轴的平行线交AB于D.‎ ‎ ‎ 当x=－时，△PAB的面积的最大值为，此时.‎ ‎23. 解：（1）⊙P与x轴相切.‎ ‎ ∵直线y=－2x－8与x轴交于A（4，0），‎ 与y轴交于B（0，－8），‎ ‎∴OA=4，OB=8.‎ 由题意，OP=－k，‎ ‎∴PB=PA=8+k.‎ 在Rt△AOP中，k2+42=(8+k)2，‎ ‎∴k=－3，∴OP等于⊙P的半径，‎ ‎∴⊙P与x轴相切.‎ ‎（2）设⊙P与直线l交于C，D两点，连结PC，PD当圆心P在线段OB上时,作PE⊥CD于E.‎ ‎∵△PCD为正三角形，∴DE=CD=，PD=3，‎ ‎ ∴PE=.‎ ‎∵∠AOB=∠PEB=90°， ∠ABO=∠PBE，‎ ‎∴△AOB∽△PEB，‎ ‎∴，‎ ‎∴‎ ‎∴，‎ ‎∴，‎ ‎∴.‎ 当圆心P在线段OB延长线上时,同理可得P(0,－－8)，‎ ‎∴k=－－8，‎ ‎∴当k=－8或k=－－8时，以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.‎