数学中考总复习30讲一轮复习等腰三角形 9页

第18讲 等腰三角形 ‎【考点总汇】‎ 一、等腰三角形的判定与性质 ‎1.判定：如果一个三角形有两个角相等，那么这两个角所对的边也 （简写“ ”）。‎ ‎2.性质 ‎ ‎（1）等腰三角形的两个底角 （简写为“ ”）。 ‎ ‎（2）等腰三角形顶角的 、底边上的高和底边上的 互相重合（简写成“三线合一”）。‎ ‎（3）等腰三角形是 图形，底边上的中线（或底边上的高或顶角的平分线）所在的直线是它的对称轴。‎ 微拨炉：‎ ‎1.等腰三角形的定义既是等腰三角形的一个性质，又是等腰三角形的一种判定方法。‎ ‎2.等腰三角形性质是已知两腰相等得出两角相等，而等腰三角形的判定则是已知两角相等得出两边相等。二者题设和结论正好相反，注意不要混淆。‎ 二、等边三角形的判定与性质 ‎1.判定 ‎（1）三个角 的三角形是等边三角形。‎ ‎（2）有一个角等于60的 三角形是等边三角形。 ‎ ‎2.性质 ‎（1）等边三角形的三个内角都 ，并且每一个角都等于 。‎ ‎（2）等边三角形是轴对称图形，并且有 条对称轴。‎ 微拨炉：‎ ‎1.由于等边三角形是特殊的等腰三角形，所以等边三角形具有等腰三角形的所有性质，但等边三角形具有的性质等腰三角形不一定具有。‎ ‎2.等边三角形的性质和判定的题设和结论也正好相反，要注意区别。‎ 三、线段的垂直平分线 ‎1.性质：线段垂直平分线上的点与这条线段两个端点的距离 。‎ ‎2.判定：与一条线段两个端点距离相等的点，在这条线段的 上。‎ 微拨炉：‎ ‎1.线段的垂直平分线的性质是证明线段相等或垂直的重要方法。‎ ‎2.垂直平分线的性质与判定的题设和结论也正好相反，注意区别。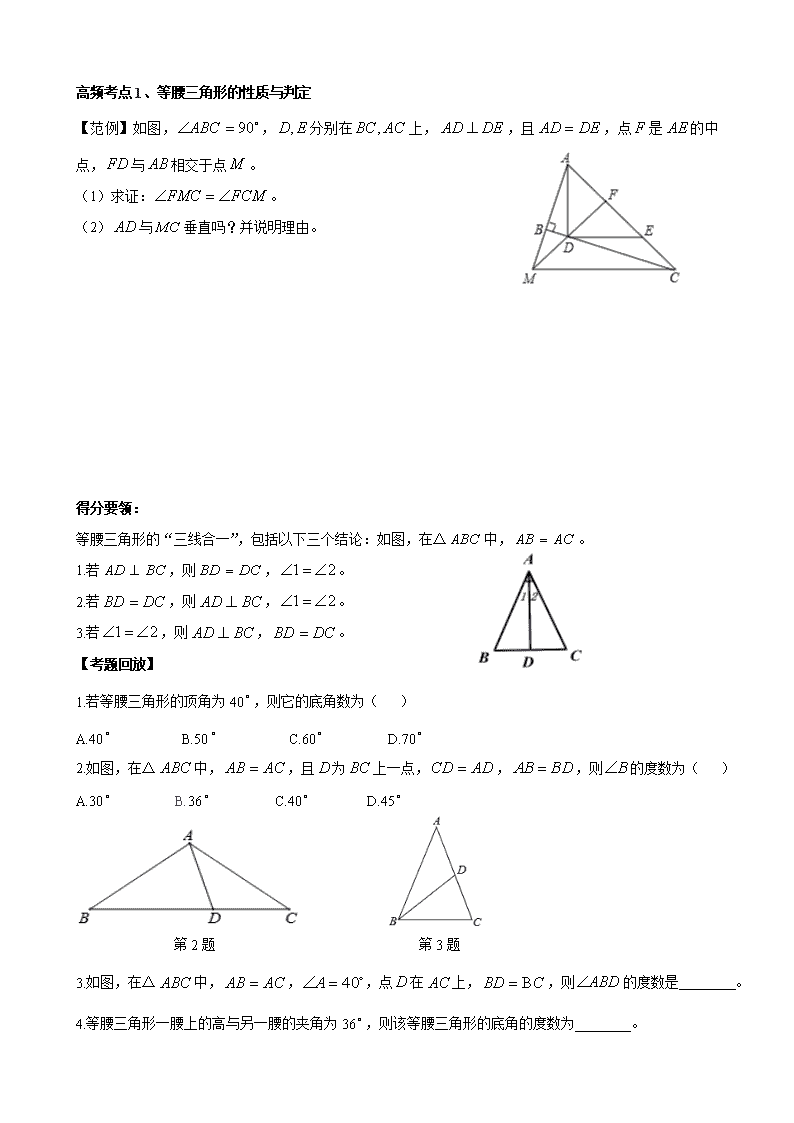‎ 高频考点1、等腰三角形的性质与判定 ‎【范例】如图，，分别在上，，且，点是的中点，与相交于点。‎ ‎（1）求证：。 ‎ ‎（2）与垂直吗？并说明理由。‎ 得分要领：‎ 等腰三角形的“三线合一”，包括以下三个结论：如图，在△中，。‎ ‎1.若，则，。‎ ‎2.若，则，。‎ ‎3.若，则，。‎ ‎【考题回放】‎ ‎1.若等腰三角形的顶角为40，则它的底角数为（ ）‎ A.40 B.50 C.60 D.70‎ ‎2.如图，在△中，，且为上一点，，，则的度数为（ ）‎ A.30 B.36 C.40 D.45‎ ‎ ‎ 第2题 第3题 ‎3.如图，在△中，，，点在上，，则的度数是 。‎ ‎4.等腰三角形一腰上的高与另一腰的夹角为36，则该等腰三角形的底角的度数为 。‎ ‎5.如图，在△中，点分别在边上，与交于点，给出下列三个条件：①；②；③。‎ ‎（1）上述三个条件中，由哪两个条件可以判定△是等腰三角形？（用序号写出所有在立的情形）‎ ‎（2）请选择（1）中的一种情形，写出证明的过程。‎ 高频考点2、等边三角形的性质与判定 ‎【范例】如图，在等边三角形中，点分别在边上，且∥，过点作，交的延长线于点。‎ ‎（1）求的度数。 ‎ ‎（2）若，求的长。‎ 得分要领：‎ 等边三角形是特殊的等腰三角形，解题时，要灵活运用下列性质：（1）三条边相等。（2）三个角相等，并且都等于60。（3）是轴对称图形，并且有三条对称轴。（4）具有“等边对等角”及“三线合一”的性质。‎ ‎【考题回放】‎ ‎1.如图，等边△中，点分别为边的中点，则的度数为（ ）‎ A.30 B.60 C.120 D.150 ‎ 第1题 第2题 ‎2.如图，△和△均是等边三角形，分别与交于点，有如下结论：‎ ‎①△≌△；②；③。其中，正确结论的个数是（ ）‎ A.3个 B.2个 C.1个 D.0个 ‎ ‎3.如图，已知矩形，把矩形沿直线折叠，点落在点 处，连接，若△是等边三角形，则 。‎ 高频考点3、线段垂直平分线的性质与判定 ‎【范例】如图，在Rt△中，，分别以点为圆心，大于长为半径画弧，两弧相交于点连接，与分别交于点，连接。‎ ‎（1）求。（直接写出结果）‎ ‎（2）当，时，求△的周长。‎ 得分要领：‎ 线段垂直平分线的应用特征 ‎1.线段垂直平分线中的两组线段相等：①线段垂直平分线上的点到线段两个端点的距离相等；②被垂直平分的线段，被分为两条相等的线段。‎ ‎2.当出现“垂直平分”字眼或题目中有垂直，且垂足是中点时，要联想到线段垂直平分线的性质。‎ ‎【考题回放】‎ ‎1.在△中，按以下步骤作图：①分别以为圆心，以大于的长为半径作弧，两弧相交于两点；②作直线交于点，连接。若，，则的度数为 。‎ ‎2.如图，等腰△中，，，的垂直平分线交于点，则的度数是 。‎ 第2题 第3题 ‎3.如图，Rt△中，，垂直平分，垂足为，∥，且，，则的长为 。‎ ‎【错误诊断】分析下面解题的错误并纠正在右边 ‎【例题】等腰三角形一腰长为5，一边上的高为3，则 底边长为 。‎ 解：若3是该等腰三角形底边上的高，如图1‎ 此时由勾股定理得：，则底 图1 ‎ 若3是该等腰三角形腰上的高，等腰三角形为锐角三角形时， ‎ 如图2，由勾股定理易得，则 在Rt△中，由勾股定理得：‎ 答案：8或 ‎ ‎ 图2‎ ‎【规避策略】‎ ‎1.确定底和腰。当已知等腰三角形的两边时，要先确定哪条边作腰或底边，分情况进行讨论。‎ ‎2.注意高的位置。当等腰三角形的顶角不确定时，这个三角形有可能是锐角三角形，也有可能是钝角三角形，也要进行分类讨论。‎ ‎【实战演练】‎ ‎1.等腰三角形两边长分别为4和8，则这个等腰三角形的周长为（ ）‎ A.16 B.18 C.20 D.16或20‎ ‎2.已知等腰三角形一腰上的高与另一腰的夹角为60，则这个等腰三角形的顶角是（ ）‎ A.30 B.60 C.150 D.30或150‎ ‎3.如图，在△中，，，的垂直平分 线交于，交于，下述结论错误的是（ ）‎ A.平分 B.△的周长等于 ‎ C. D.点是线段的中点 ‎4.如图，△是等边三角形，是的平分线上一 点，于点，线段的垂直平分线交于点，‎ 垂足为点，若，则的长为（ ）‎ A.2 B. C. D.3 ‎ ‎5.如图，△和△都是边长为4的等边三角形，点在同一条直线上，连接，则的长为（ ）‎ A. B. 　 C. 　 D.‎ ‎6.如图，是△的角平分线，，，则图中的等腰三角形有 个。‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 第6题 第7题 ‎7.如图，△中，的平分线相交于点，过作∥，若，则等于 。‎ ‎8.如图，点在上，，，，与交于点。‎ ‎（1）求证：。‎ ‎（2）判断△的形状，并说明理由。‎ ‎9.如图，已知△为等边三角形，点分别在边上，且，与相交于点。（1）求证：△≌△。 ‎ ‎（2）求的度数。‎ ‎10.如图，△是等边三角形，点是上一点，，。请判断△的形状，并说明理由。‎ ‎【限时小测】建议用时30分钟。总分50分 一、选择题（每小题3分，共12分）‎ ‎1.如图，已知，点在边上，，点在边上，，若，则（ ）‎ A.3 B.4 C.5 D.6‎ ‎ ‎ 第1题 第2题 ‎2.如图，在△中，，，cm，的垂直平分线交于点，交于点，的垂直平分线交于点，交于点，则的长为（ ）‎ A.4cm B.3cm C.2cm D.1cm ‎3. 如图，在△中，，，分别是△，△的角平分线，则图中的等腰三角形有（ ）‎ A.2个 B.3个 C.4个 D.5个 ‎ 第3题 第4题 ‎4.如图所示，在等边△中，高相交于点，连接，则的度数是（ ）‎ A.15 B.20 C.25 D.30‎ 二、填空题（每小题4分，共12分）‎ ‎5.若等腰三角形的一个内角为50，则它的顶角为 。‎ ‎6.已知等腰三角形的两边长分别为，且满足，则此等腰三角形的周长为 。‎ ‎7.如图钢架中，焊上等长的13根钢条来加固钢架，若…，则的度数是 。‎ 三、解答题（共26分）‎ ‎8.（12分）如图①，在△中，，点是的中点，点在上。‎ ‎（1）求证：。‎ ‎（2）如图②，若的延长线交于点，且，垂足为，，原题设其他条件不变。求证：△≌△。‎ ‎【培优训练】‎ ‎9.（14分）（1）如图1，在等边△中，点是上的任意一点（不含端点），连接，以为边作等边△，连接。求证：。‎ ‎（2）如图2，在等边△中，点是延长线上的任意一点（不含端点），其他条件不变，还成立吗？请说明理由。‎