2017厦门双十中考二模—数学 11页

‎2016—2017厦门双十中学中考数学第二次模拟考试 班级 姓名 座号 ‎ 一、 选择题：（共10小题，每题4分，共40分）命卷人：陈媚娜 审卷人：张建怀 ‎1.表示( )‎ A.的倒数 B. 的相反数 C. 的绝对值 D. 的算术平方根 ‎2. 我国最大的领海是南海，总面积有3 500 000平方公里，数据3 500 000用科学记数法表示应为（ ）‎ ‎ A． B． C． D．‎ ‎3.若∠A 与∠B 互为补角，则∠A＋∠B＝（ ） ‎ A.180° B.120° C.90° D .60°‎ ‎4．钟鼎文是我国古代的一种文字，是铸刻在殷周青铜器上的铭文，下列钟鼎文中，不是轴对称图形的是（ ）‎ ‎ A. B. C. D. ‎ ‎5.不等式组的解集是（　 　）‎ A．x≤2 B．x＞1 C．1＜x≤2 D．无解 ‎6.下列各式运算结果为的是( )‎ A． 　 B. C. D.‎ ‎7.正六边形ABCDEF内接于⊙O，⊙O的半径为2，则 的长为( )．‎ A. B. C. D.‎ ‎8．一组数据6,6,6,6,6,6,6的方差为m，若增加一个数0，则新数据的方差比原数据的方差是（ ）‎ A.变大 B.减小 C. 不变 D.无法确定 ‎9. 已知点A(2,b),B(-2,-b),C(b,2)在同一函数图像上,这个函数图像可以是（ ）‎ A．B．C．D．‎ ‎10.平 面 直 角 坐 标 系 中， 已 知□ABCD的 四 个 顶 点 坐 标 分 别 是 ‎，，，，则所满足的关系式是 ( ).‎ A. B. C. D. ‎ 二．填空题：（共6小题，每题4分，满分24分）‎ ‎11．如果分式有意义，那么x的取值范围是__________．‎ ‎12．计算：= ．‎ ‎13.一天上午林老师来到某中学参加该校的校园开放日活动，他打算随机听一节九年级的课程，下表是他拿到的当天上午九年级的课表，如果每一个班级的每一节课被听的可能性是一样的，那么听数学课的可能性是__________．‎ ‎14.如图，已知四边形ABCD为平行四边形，对角线AC，BD相交于点O,要使四边形ABCD为菱形，需要增加的一个条件是： ．（只填一个你认为正确的条件即可，不添加任何线段与字母）‎ ‎15．数学活动课上，老师让同学们围绕一道尺规作图题展开讨论，尽可能想出不同的作法：‎ 已知：如图，直线L和L外一点P.‎ 求作：直线PQ，使PQ⊥L于点Q．‎ 小强的作法如下：‎ ‎1.在直线L上任取一点A，连接PA；‎ ‎2.分别以A，P为圆心，以大于AP长为半径 作弧，两弧交于C，D两点；‎ ‎3.作直线CD，交AP于点O；‎ ‎4.以O为圆心，以OA长为半径作圆，交直线L于点Q；‎ ‎5.作直线PQ. ‎ 所以直线PQ即为所求.‎ 老师说：“小强的作法正确．”‎ 请回答：小强这样作图的依据是: ．‎ ‎16.我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”（如图1）。图2由弦图变化得到，它是由八个全等的直角三角形拼接而成。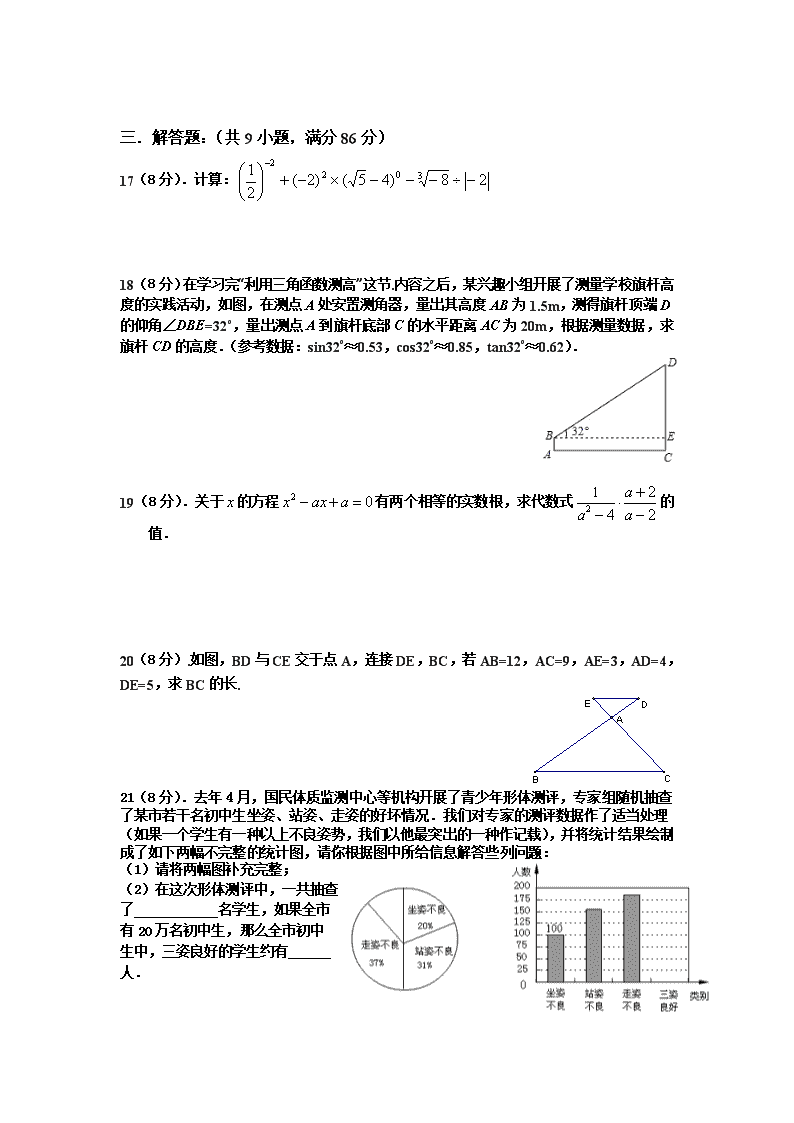记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为，，.‎ 若＋＋＝21，则的值是 ．‎ 三．解答题：（共9小题，满分86分）‎ ‎17（8分）．计算：‎ ‎18（8分）在学习完“利用三角函数测高”这节.内容之后，某兴趣小组开展了测量学校旗杆高度的实践活动，如图，在测点A处安置测角器，量出其高度AB为1.5m，测得旗杆顶端D的仰角∠DBE=32°，量出测点A到旗杆底部C的水平距离AC为20m，根据测量数据，求旗杆CD的高度．（参考数据：sin32°≈0.53，cos32°≈0.85，tan32°≈0.62）．‎ ‎19（8分）．关于的方程有两个相等的实数根，求代数式的值．‎ ‎20（8分）.如图，BD与CE交于点A，连接DE，BC，若AB=12，AC=9，AE=3，AD=4，DE=5，求BC的长.‎ ‎21（8分）．去年4月，国民体质监测中心等机构开展了青少年形体测评，专家组随机抽查了某市若干名初中生坐姿、站姿、走姿的好坏情况．我们对专家的测评数据作了适当处理（如果一个学生有一种以上不良姿势，我们以他最突出的一种作记载），并将统计结果绘制成了如下两幅不完整的统计图，请你根据图中所给信息解答些列问题： ‎ ‎（1）请将两幅图补充完整；‎ ‎（2）在这次形体测评中，一共抽查了　　　　　　名学生，如果全市有20万名初中生，那么全市初中生中，三姿良好的学生约有　　　人．‎ ‎22（10分）.如图，已知△ABC中，AB = AC，以AB为直径的⊙O交 BC于点D，过D作DE⊥AC于E.‎ ‎ (1)求证：直线DE是⊙O的切线；‎ ‎ (2)若CD=,∠ACB = 30°，分别求AB，OE的大小。‎ ‎23（10分）.某加气站某日的储气量为10000立方米．从7︰00开始,工作人员给在加气站排队等候的若干辆车加气,假设加气过程中每把加气枪均以每小时200立方米的速度为汽车加气．设加气站的储气量为y（立方米），加气总时间为x（小时）（加气期间关闭加气枪的时间忽略不计）．加气站加气枪的使用数量如下表所示：‎ 时间段 ‎7︰00—7︰30‎ ‎7︰30—8︰00‎ ‎8︰00以后 加气枪使用︰数量 ‎（单位：把）‎ ‎3‎ ‎5‎ ‎6‎ ‎（1）分别求出7︰00—7︰30及8︰00之后加气站的储气量y（立方米）与时间x（小时）的函数关系式．‎ ‎（2）若每辆车的加气量均为20立方米，请通过计算说明前50辆车能否在当天8︰00之前加完气．‎ ‎24（13分）.如图，正方形ABCD中，点E为边BC上的一点.‎ ‎(1)用尺规在DC上确定一点F,使得，并说明理由（保留作图痕迹，不写作法）‎ ‎(2) 在（1）的条件下，若AF与DE相交于点P,连接PC，点E为BC的中点， PE＝6，‎ PC＝，求PF的长 ‎(3) 在（1）的条件下若正方形边长为4，直接写出PB的最小值_______.‎ ‎25（13分）在平面直角坐标系xOy中，对于点和点，给出如下定义：‎ 若，则称点为点的限变点．例如：点的限变点的坐标是，点的限变点的坐标是．‎ ‎（1）点的限变点的坐标是___________；‎ ‎（2）若点在函数的图象上，其限变点的纵坐标的取值范围是，求的取值范围；‎ ‎（3）若点在关于的二次函数的图象上，其限变点的纵坐标的取值范围是或，其中．令，求关于的函数解析式及的取值范围．‎ ‎2016—2017厦门双十中学中考数学第二次模拟考试答案 一、选择题 C,D,A,D,C, B,B,A,B,D 二、填空题 11. ‎ 12. 13. 14. （或）‎ ‎15. 直径所对的圆周角是直角 16. 7‎ 三、解答题 18. 解：∵∠A＝∠C＝∠BEC＝90°，‎ ‎∴ 四边形ABEC为矩形 ‎ ‎∴ BE＝AC＝20, CE＝AB＝1.5-------------------2‎ ‎ 在Rt△BED中，∴ tan∠DBE＝即tan32°＝----------------6‎ ‎ ∴ DE＝20×tan32°12.4, CD＝CE＋DE13.9. [------------------8‎ ‎---‎ 答：旗杆CD的高度约为13.9 m.‎ 19. ‎∵关于的方程有两个相等的实数根 ‎ ∴---------------------2分 ‎ ‎ ‎---------------- 4分 ‎-------------------6分 ‎ ‎ ‎----------------------8分 18. ‎ 法一∵AE=3，AD=4，DE=5‎ ‎ ∴,-------------1分 ‎ ∴------------------3分 ‎ ∴‎ ‎ ∵‎ ‎ ∴-----------------4分 ‎ ‎ 在中------------6分 ‎ ∵AB=12，AC=9‎ ‎ ∴ ------------------8分 法二：判断相似，利用相似性质计算 ‎21.:（1）如图： （1）一个图2分，共4分 ‎（2）在这次形体测评中，一共抽查了　500 名学生，如果全市有20万名初中生，那么全市初中生中，三姿良好的学生约有　24000　　人．（毎空2分）‎ ‎22.（1）∵OD=OB，‎ ‎ ∴∠B=∠ODB， ∵AB=AC，‎ ‎ ∴∠B=∠C， ∴∠C=∠ODB， ∴OD∥AC，---------------2分 ∴∠ODE=∠DEC； ∵DE⊥AC， ∴∠DEC=90°， ∴∠ODE=90°， 即DE⊥OD， ∴DE是⊙O的切线．-----------4分 （2） ‎∵AB为直径 ‎ ∴‎ ‎ ∵ AB = AC ∠ACB = 30°‎ ‎ ∴ BD=DC ‎ ‎ ∵ CD=‎ ‎ ∴ BD= --------------------5分 ‎ 在中 ‎ ∴AB=----------7分（只要求出AB或AC，都7分）‎ ‎ ∴ OD=OB==2‎ ‎ 在中 ‎ ∴DE= ---------------------9分 在中 ‎∴ -------------------------------10分 ‎24.（1）保留作图痕迹，以D为圆心，CE长为半径画弧，交DC于F---------------------1分 ‎ 易证△ADF≌△DCE--------------------------------------------------------------------------4分 ‎ （2）法1：设PF=a，易证△DPF∽△APD∽△ADF，------------------------------------6分 ‎ ∴PF:DP=DP:AP=DF:AD=1:2----------------------------------7分 ‎ ∴DP=2a，AP=4a，AF=DE=5a ‎ ∴PE=3a=6-------------------8分 ‎ ∴a=2‎ ‎ ∴PF=2-----------------------9分 ‎ 法2：作CM⊥PC交PF延长线于点M，易证△PEC≌△MFC----------------6分 ‎ ∴PC=CM= MF=PE=6------------------7分 ‎ ∴在Rt△PCM中，PM=-------8分 ‎ ∴PF=2----------9分 ‎ （3）---------------------13分 ‎25.解：（1） ； ……………………………3分 ‎（2）依题意，图象上的点P的限变点必在函数的图象上．‎ ‎，即当时，取最大值2．‎ 当时，．‎ ‎． ………………………………………5分 当时，或．‎ 或． ………………………………7分 ‎，‎ 由图象可知，的取值范围是．‎ ‎……………………………………………8分 （3） ‎，‎ 顶点坐标为．………………………………………………………………9分 若，的取值范围是或，与题意不符．‎ 若，当时，的最小值为，即；‎ ‎ 当时，的值小于，即．‎ ‎．‎ 关于的函数解析式为 ． ……………………………11分 当t=1时，取最小值2．‎ 的取值范围是≥2． ………………………………………………………13分