- 1.61 MB
- 2021-05-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2014年安徽省初中毕业学业考试数学试题
一、选择题(本大题共10小题,每小题4分,满分40分)
1、(-2)×3的结果是( )
A、-5 B、1 C、-6 D、6
2、x2·x4=( )
A、x6 B、x5 C、x8 D、x9
3、如图,;图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视图是( )
A B C D
4、下列四个多项式中,能因式分解的是( )
A、a2+1 B、a2-6a+9 C、x2+5y D、x2-5y
5、某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如右表,则棉花纤维长度的数据在8≤x<32这个范围的频率为( )
棉花纤维长度x
频数
0≤x<8
1
8≤x<16
2
16≤x<24
8
24≤x<32
6
32≤x<40
3
A、0.8 B、0.7 C、0.4 D、0.2
6、设n为正整数,且n<<n+1,则n的值为( )
A、5 B、6 C、7 D、8
7、已知x2-2x-3=0,则2x2-4x的值为( )
A、-6 B、6 C、-2或6, D、-2或30
8、如图,RtΔABC中,AB=9,BC=6,∠B=900,将ΔABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A、 B、 C、4 D、5
9、如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
C
B
D
A
10、如图,正方形ABCD的对角线BD长为2,若直线l满足:(1)点D到直线l的距离为,(2)A、C两点到直线l的距离相等,则符合题意的直线l的条数为( )
A、1 B、2 C、3 D、4
二、填空题(本大题共4小题,每小题5分,满分20分)
11、据报载,2014年我国将发展固定宽带接入新用户25000000户,其中25000000用科学记数法表示为
F
A
E
D
C
B
12.某厂今年一月份新产品的研发资金为a元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y=
13.方程=3的解是x=
14.如图,在 ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
三、(本大题共2小题,每小题8分,满分16分)
15、计算:--(-π)0+2013
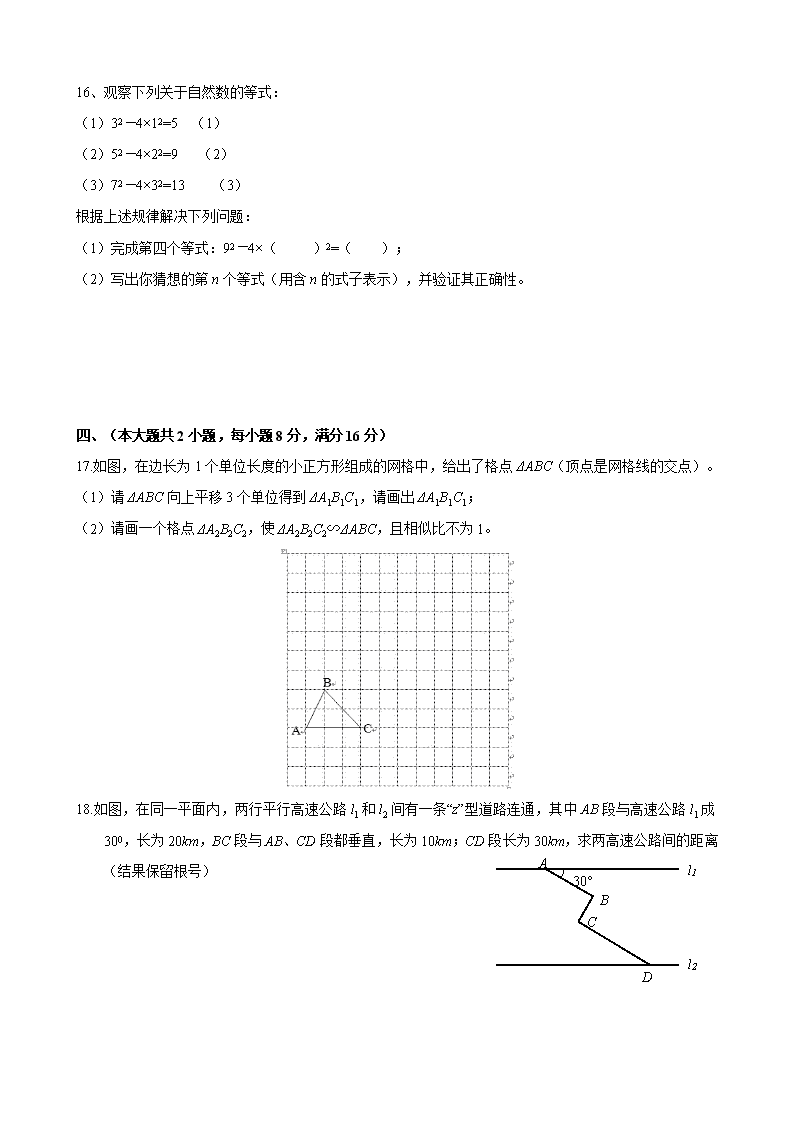
16、观察下列关于自然数的等式:
(1)32-4×12=5 (1)
(2)52-4×22=9 (2)
(3)72-4×32=13 (3)
根据上述规律解决下列问题:
(1)完成第四个等式:92-4×( )2=( );
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性。
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点ΔABC(顶点是网格线的交点)。
(1)请ΔABC向上平移3个单位得到ΔA1B1C1,请画出ΔA1B1C1;
(2)请画一个格点ΔA2B2C2,使ΔA2B2C2∽ΔABC,且相似比不为1。
A
B
C
D
l1
l2
30°
18.如图,在同一平面内,两行平行高速公路l1和l2间有一条“z”型道路连通,其中AB段与高速公路l1成300,长为20km,BC段与AB、CD段都垂直,长为10km;CD段长为30km,求两高速公路间的距离(结果保留根号)
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在⊙O中,半径OC与弦AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点,若OE=4,OF=6,求⊙O的半径和CD的长。
20.2013年某企业按餐厨垃圾处理费25元/吨,建筑垃圾处理费16元/吨标准,共支付餐厨和建筑垃圾处理费5200元,从2014年元月起,收费标准上调为:餐厨垃圾处理费100元/吨,建筑垃圾处理费30元/吨,若该企业2014年处理的这两种垃圾数量与2013年相比没有变化,就要多支付垃圾处理费8800元,
(1)该企业2013年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2014年将上述两种垃圾处理量减少到240吨,且建筑垃圾处理费不超过餐厨垃圾处理量的3倍,则2014年该企业最少需要支付这两种垃圾处理费共多少元?
六、(本题满分12分)
21.如图,管中放置着三根同样绳子AA1、BB1、CC1。
(1)小明从这三根绳子中随机选一根,恰好选中绳子AA1的概率是多少?
B1
B
C1
A1
A
C
(2)小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,求这三根绳子连结成一根长绳的概率。
七、(本题满分12分)
22.若两个二次函数图象的顶点,开口方向都相同,则称这两个二次函数为“同簇二次函数”。
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2-4mx+2m2+1,和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2为y1为“同簇二次函数”,求函数y2的表达式,并求当0≤x≤3时,y2的最大值。
八、(本题满分14分)
23.如图1,正六边形ABCDEF的边长为a,P是BC边上一动点,过P作PM∥AB交AF于M,作PN∥CD交DE于N,
P
N
M
F
E
D
C
B
A
(1)∠MPN=
(2)求证:PM+PN=3a
O
N
M
F
E
D
C
B
A
P
(2)如图2,点O是AD的中点,连接OM、ON。求证:OM=ON
(3)如图3,点O是AD的中点,OG平分∠MON,判断四边形OMGN是否为特殊四边形,并说明理由。
O
N
M
F
E
D
C
B
A
P
G