中考数学专题复习一次函数无答案 2页

‎1.已知m是整数，且一次函数y=(m＋4)x＋m＋2的图像不经过第二象限，则m=__ .‎ ‎2.—次函数y＝(a—2)x＋4a—3的图像与y轴的交点在x轴的下方，则a的取值范围是______.‎ ‎3.已知直线y=kx+b与直线y=−3x+7关于x轴对称，则直线解析式为____________‎ ‎4.已知直线y=kx+b与直线y=−3x+7关于Y轴对称，则直线解析式为____________‎ ‎5.一次函数y=mx+n(m≠0)，当−2≤x≤5时，对应的y值为0≤y≤7，则一次函数的解析式为_______________________________________.‎ ‎6.在平面直角坐标系中，线段AB的端点坐标为A（-2,4），B（4,2），直线y=kx-2与线段AB有交点，则k的取值范围是______________.‎ ‎7.如图所示，在同一直角坐标系中，一次函数y=k1x、y=k2x、y=k3x、y=k4x的图象分别为l1、l2、l3、l4，则k1，k2，k3，k4的大小关系是_____________________.‎ ‎8.已知一次函数y=kx+b与直线y=3x−2平行,与直线y=2x+3相交于y轴上一点,则k、b的值分别为______________________.‎ ‎9.直线l1向右平移3个单位，再向下平移2个单位，得到直线l2解析式为y=2x-1，则直线l1的解析式为_______________________.‎ ‎10.把直线y=-3x向上平移后得到直线AB，直线AB经过点（m，n），且3m＋n=8，则直线AB的解析式是_________________________.‎ ‎11.在平面直角坐标系中,已知直线y=−x+3与x,y轴分别交于A. B两点,点C(0,n)是y轴上一点,把坐标平面沿AC折叠,使点B刚好落在x轴上,则点C的坐标为____.‎ ‎12.已知关于x的一次函数y=mx+2m-7在-1≤x≤5上的函数值总是正数，则m的取值范围是_________________.‎ ‎13.已知关于x的一次函数y=nx+2n−1，无论n为何值时图象恒过一定点，则此定点坐标为___________.‎ ‎14.已知一次函数y=3x+m的图像与x轴的焦点到y轴的距离为4，求其函数解析式为____________________.‎ ‎15.在平面直角坐标系中。过一点分別作坐标轴的垂线，若与坐标轴围成矩形的周长的数值与面积的数值相等，则这个点叫做和谐点。例如。图中过点P分別作x轴，y轴的垂线。与坐标轴围成矩形OAPB的周长的数值与面积的数值相等，则点P是和谐点,若和谐点P(a,3)在直线y=−x+b(b为常数)上，则a=________,b=__________.‎ ‎16.如图,A(0,1),M(3,2),N(4,4).动点P从点A出发，沿y轴以每秒1个单位长的速度向上移动，且过点P的直线l: y=−x+b也随之移动，设移动时间为t秒.‎ ‎(1)当t=3时，l的解析式为________________‎ ‎(2)若点M，N位于l的异侧，t的取值范围是_____________‎ ‎(3)当t=________时，点M关于l的对称点落在坐标轴上.‎ ‎ (7题图） （15题图） （16题图） （18题图） ‎ ‎17.无论m为何值直线y=x+2m与直线y=−x+4的交点都不可能在第______象限。‎ ‎18.如图所示,函数y1=|x|和y2=x+的图象相交于(−1,1),(2,2)两点.当y1>y2时，x的取值范围是______________.‎ ‎19.若直线y=−2x−4与直线y=4x+b的交点在第三象限,则b的取值范围是______.‎ ‎20.已知一次函数y=ax+b的图象过第一、二、四象限,且与x轴交于点(2,0),则关于x的不等式a(x−1)−b>0的解集为_______________.‎ ‎21.已知函数y=−x+m与y=mx−4的图象的交点在x轴的负半轴上，那么m=____.‎ ‎22.对于三个数a、b、c,用min{a,b,c}表示这三个数中最小的数,例如,min{−1,2,3}=−1,min{−1 ,2 , a}= .那么观察图象,可得到min{x+1,2−x,2x−1}的最大值为___.‎ ‎23.如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠a=75∘,则b的值为___________.  ‎ ‎24.如图,直线y=−x+2与x轴、y轴分别交于A. B两点,把△AOB绕点A顺时针旋转60∘后得到△AO′B′,则点B′的坐标是______.‎ ‎(22题图) （23题图） （24题图）‎ 25. 平面直角坐标系中,O是坐标原点,点A的坐标是(4,0),点P在直线y=−x+m上,且AP=OP=4.则m的值为__________‎ 26. 若函数y=−x−4与x轴交于点A，直线上有一点M，若△AOM的面积为8，则点M的坐标为_________.‎ 27. 在直角坐标系中,O为坐标原点,已知A(1,a)在直线y=-x+2上，,在坐标轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有________.‎ 28. 直线y=X+1和x轴、y轴分别交于点A. B. 若以线段AB为边作等边三角形ABC，则点C的坐标是_______.‎ 29. 如图，点A的坐标为（﹣1，0），点B在直线y=x上运动，当线段AB最短时，点B的坐标为________.‎ 25. 在平面直角坐标系中有两点A(−2,2),B(1,4)，根据要求求出P点坐标：‎ 26. ‎(1)在x轴上找一点P，使得PA+PB最小,则p坐标为________‎ (2) 在x轴上找一点P，使得|PA−PB|最大,则p坐标为________‎ ‎32.探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的有关问题，这种方法称为面积法。请你运用面积法求解下列问题：在等腰三角形ABC中，AB=AC，BD为腰AC上的高。‎ ‎(1)若BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为h1,h2.‎ A. 若M在线段BC上,h1,h2,h之间的关系为_______________；‎ B. 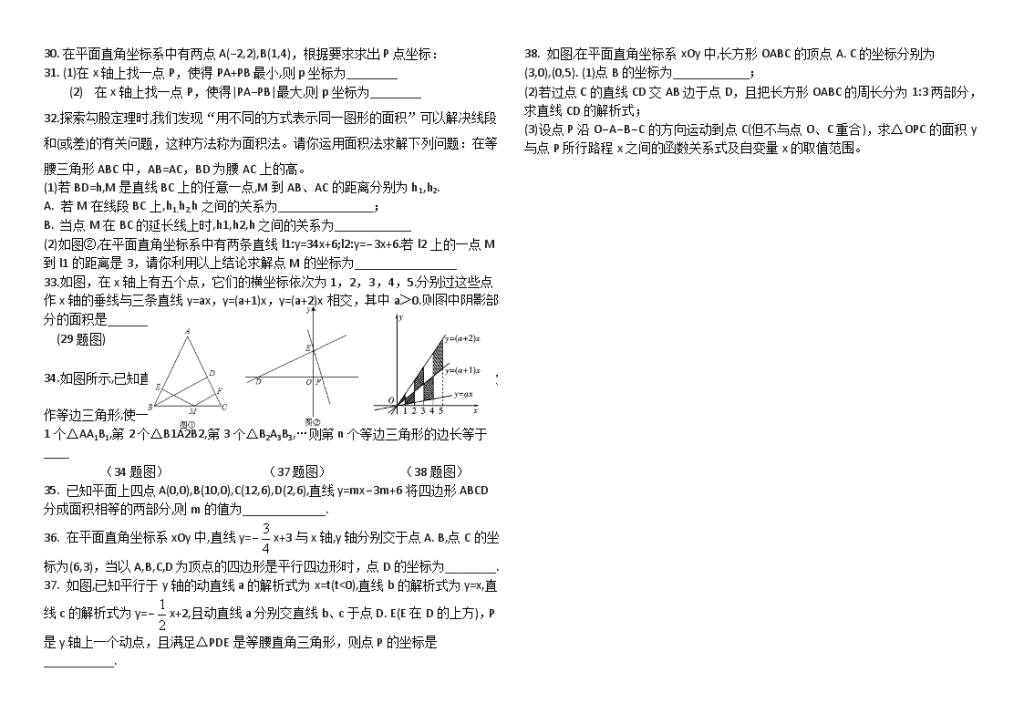当点M在BC的延长线上时,h1,h2,h之间的关系为____________‎ ‎(2)如图②,在平面直角坐标系中有两条直线l1:y=34x+6;l2:y=−3x+6.若l2上的一点M到l1的距离是3，请你利用以上结论求解点M的坐标为________________‎ ‎33.如图，在x轴上有五个点，它们的横坐标依次为1，2，3，4，5.分别过这些点作x轴的垂线与三条直线y=ax，y=(a+1)x，y=(a+2)x相交，其中a＞0.则图中阴影部分的面积是________________‎ ‎ (29题图) （32题图） （33题图） ‎ ‎34.如图所示,已知直线y=−x+1与x、y轴交于B. C两点,A(0,0),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第n个等边三角形的边长等于____‎ ‎ （34题图） （37题图） （38题图）‎ 35. 已知平面上四点A(0,0),B(10,0),C(12,6),D(2,6),直线y=mx−3m+6将四边形ABCD分成面积相等的两部分,则m的值为_____________.‎ 36. 在平面直角坐标系xOy中,直线y=−x+3与x轴,y轴分别交于点A. B,点C的坐标为(6,3)，当以A,B,C,D为顶点的四边形是平行四边形时，点D的坐标为________.‎ 37. 如图,已知平行于y轴的动直线a的解析式为x=t(t<0),直线b的解析式为y=x,直线c的解析式为y=−x+2,且动直线a分别交直线b、c于点D. E(E在D的上方)，P是y轴上一个动点，且满足△PDE是等腰直角三角形，则点P的坐标是___________.‎ 38. 如图,在平面直角坐标系xOy中,长方形OABC的顶点A. C的坐标分别为(3,0),(0,5). (1)点B的坐标为____________；‎ ‎(2)若过点C的直线CD交AB边于点D，且把长方形OABC的周长分为1:3两部分，求直线CD的解析式；‎ ‎(3)设点P沿O−A−B−C的方向运动到点C(但不与点O、C重合)，求△OPC的面积y与点P所行路程x之间的函数关系式及自变量x的取值范围。‎