2010年山西省中考数学试题与答案 11页

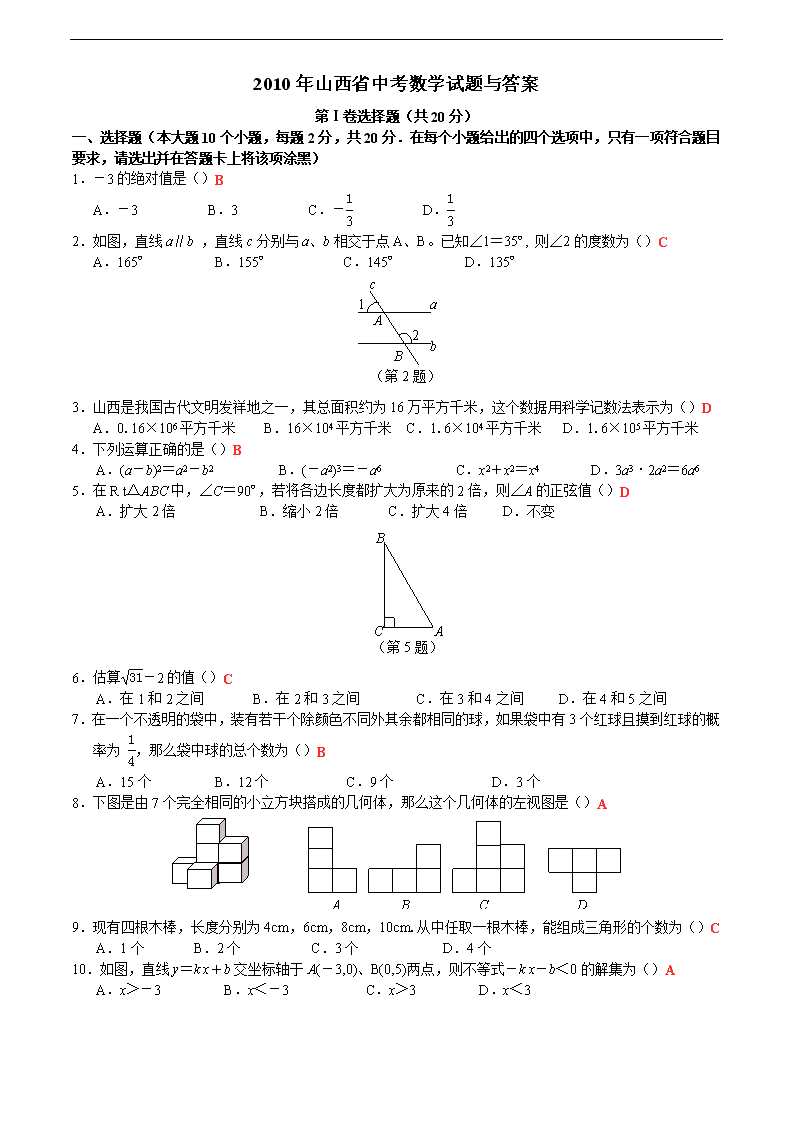
‎2010年山西省中考数学试题与答案 第Ⅰ卷选择题（共20分）‎ 一、选择题（本大题10个小题，每题2分，共20分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）‎ ‎1．－3的绝对值是（）B A．－3 B．3 C．－ D． ‎2．如图，直线a∥b ，直线c分别与a、b相交于点A、B。已知∠1＝35º, 则∠2的度数为（）C ‎ A．165º B．155º C．145º D．135º A B ‎2‎ ‎1‎ a b c ‎（第2题）‎ ‎3．山西是我国古代文明发祥地之一，其总面积约为16万平方千米，这个数据用科学记数法表示为（）D A．0.16×106平方千米 B．16×104平方千米 C．1.6×104平方千米 D．1.6×105平方千米 ‎4．下列运算正确的是（）B A．(a－b)2＝a2－b2 B．(－a2)3＝－a6 C．x2＋x2＝x4 D．3a3·2a2＝6a6‎ ‎5．在R t△ABC中，∠C＝90º，若将各边长度都扩大为原来的2倍，则∠A的正弦值（）D A．扩大2倍 B．缩小2倍 C．扩大4倍 D．不变 A B C ‎（第5题）‎ ‎6．估算－2的值（）C A．在1和2之间 B．在2和3之间 C．在3和4之间 D．在4和5之间 ‎7．在一个不透明的袋中，装有若干个除颜色不同外其余都相同的球，如果袋中有3个红球且摸到红球的概率为 ，那么袋中球的总个数为（）B A．15个 B．12个 C．9个 D．3个 ‎8．下图是由7个完全相同的小立方块搭成的几何体，那么这个几何体的左视图是（）A A B C D ‎9．现有四根木棒，长度分别为4cm，6cm，8cm，10cm.从中任取一根木棒，能组成三角形的个数为（）C A．1个 B．2个 C．3个 D．4个 ‎10．如图，直线y＝k x＋b交坐标轴于A(－3,0)、B(0,5)两点，则不等式－k x－b＜0的解集为（）A A．x＞－3 B．x＜－3 C．x＞3 D．x＜3‎ A B ‎（第10题）‎ O x y y＝k x＋b 第Ⅱ卷选择题（共100分）‎ 二、填空题（本大题共8个小题，每小题3分，共24分．把答案写在题中横线上）‎ ‎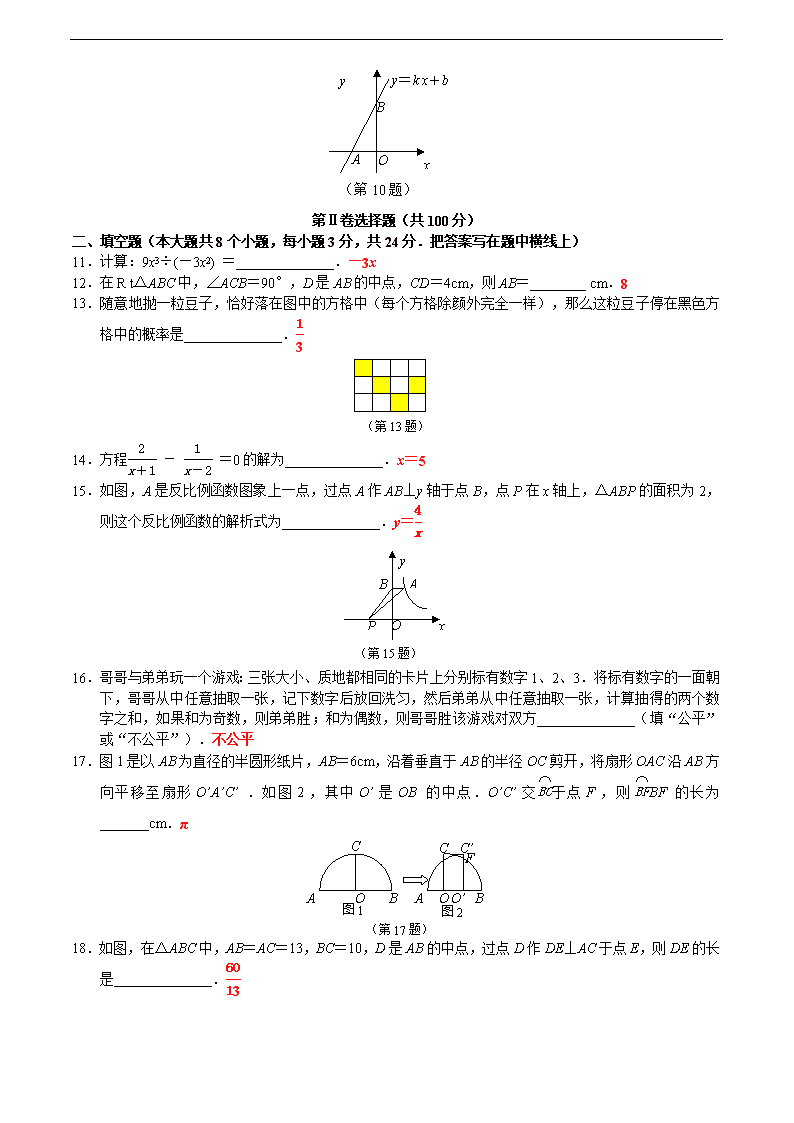11．计算：9x3÷(—3x2) ＝______________．—3x ‎12．在R t△ABC中，∠ACB＝90°，D是AB的中点，CD＝4cm，则AB＝________ cm．8‎ ‎13．随意地抛一粒豆子，恰好落在图中的方格中（每个方格除颜外完全一样），那么这粒豆子停在黑色方格中的概率是______________． ‎（第13题）‎ ‎14．方程 － ＝0的解为______________．x＝5‎ ‎15．如图，A是反比例函数图象上一点，过点A作AB⊥y轴于点B，点P在x轴上，△ABP的面积为2，则这个反比例函数的解析式为______________．y＝ ‎（第15题）‎ A B P x y O ‎16．哥哥与弟弟玩一个游戏：三张大小、质地都相同的卡片上分别标有数字1、2、3．将标有数字的一面朝 下，哥哥从中任意抽取一张，记下数字后放回洗匀，然后弟弟从中任意抽取一张，计算抽得的两个数字之和，如果和为奇数，则弟弟胜；和为偶数，则哥哥胜该游戏对双方______________（填“公平”或“不公平”）．不公平 ‎17．图1是以AB为直径的半圆形纸片，AB＝6cm，沿着垂直于AB的半径OC剪开，将扇形OAC沿AB方向平移至扇形O’A’C’ ．如图2，其中O’是OB的中点．O’C’交于点F，则BF的长为_______cm．π ‎（第17题）‎ A B O C C B A O O’‎ C’‎ 图1‎ 图2‎ F ‎18．如图，在△ABC中，AB＝AC＝13，BC＝10，D是AB的中点，过点D作DE⊥AC于点E，则DE的长是______________． A B C D E ‎（第18题）‎ 三、解答题（本大题共8个小题，共76分．解答应写出文字说明、证明过程或演算步骤）‎ ‎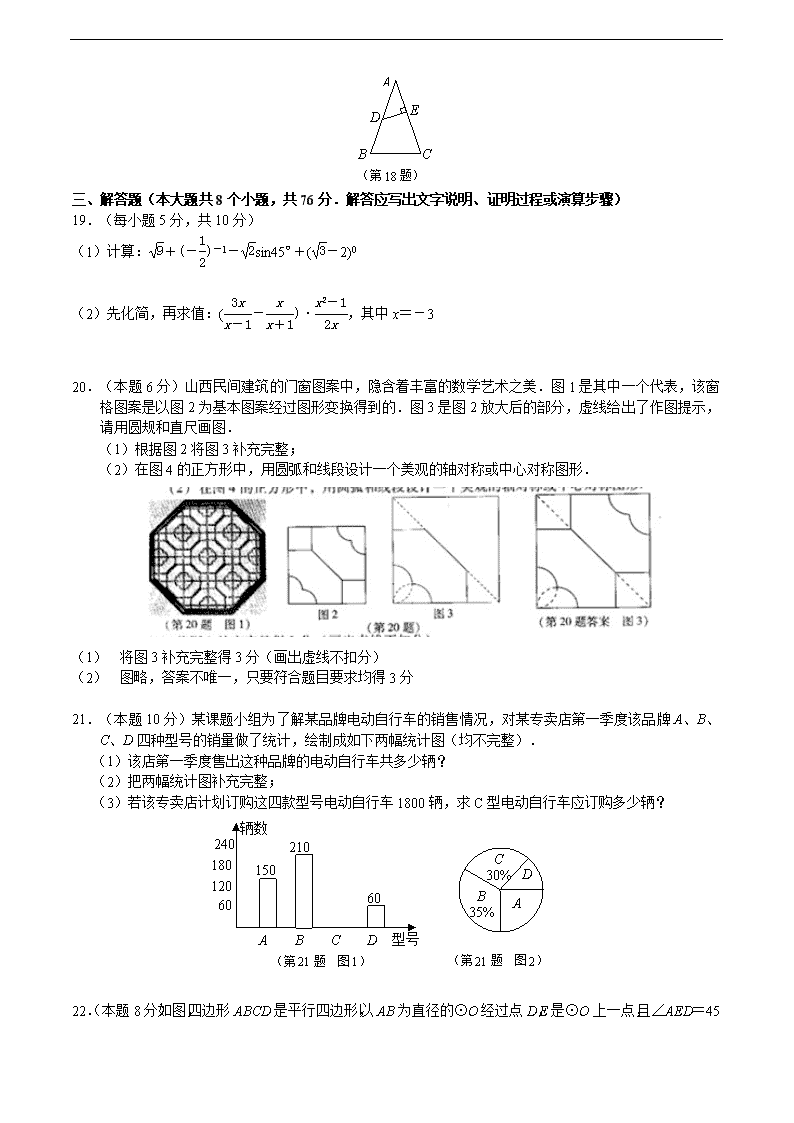19．（每小题5分，共10分）‎ ‎（1）计算：＋(－)－1－sin45º＋(－2)0‎ ‎（2）先化简，再求值：(－)·，其中x＝－3‎ ‎20．（本题6分）山西民间建筑的门窗图案中，隐含着丰富的数学艺术之美．图1是其中一个代表，该窗格图案是以图2为基本图案经过图形变换得到的．图3是图2放大后的部分，虚线给出了作图提示，请用圆规和直尺画图．‎ ‎ （1）根据图2将图3补充完整；‎ ‎（2）在图4的正方形中，用圆弧和线段设计一个美观的轴对称或中心对称图形．‎ （1） 将图3补充完整得3分（画出虚线不扣分）‎ （2） 图略，答案不唯一，只要符合题目要求均得3分 ‎21．（本题10分）某课题小组为了解某品牌电动自行车的销售情况，对某专卖店第一季度该品牌A、B、C、D四种型号的销量做了统计，绘制成如下两幅统计图（均不完整）．‎ ‎ （1）该店第一季度售出这种品牌的电动自行车共多少辆？‎ ‎ （2）把两幅统计图补充完整；‎ ‎ （3）若该专卖店计划订购这四款型号电动自行车1800辆，求C型电动自行车应订购多少辆？‎ A B C D ‎60‎ ‎（第21题 图1）‎ ‎60‎ ‎150‎ ‎210‎ ‎120‎ ‎180‎ ‎240‎ 辆数 型号 B ‎35%‎ A C ‎30%‎ D ‎（第21题 图2）‎ ‎22．（本题8分）如图，四边形ABCD是平行四边形，以AB为直径的⊙O经过点D，E是⊙O上一点，且∠‎ AED＝45º．‎ ‎ （1）试判断CD与⊙O的关系，并说明理由．‎ ‎（2）若⊙O的半径为3cm，AE＝5 cm．求∠ADE的正弦值．‎ A B C D E ‎（第22题）‎ O ‎23．（本题10分）已知二次函数y＝x2－2x－3的图象与x轴交于A、B两点（A在B的左侧），与y轴交于点C，顶点为D．‎ ‎（1）求点A、B、C、D的坐标，并在下面直角坐标系中画出该二次函数的大致图象；‎ ‎（2）说出抛物线y＝x2－2x－3可由抛物线y＝x2如何平移得到？‎ ‎（3）求四边形OCDB的面积．‎ ‎24．（本题8分）某服装店欲购甲、乙两种新款运动服，甲款每套进价350元，乙款每套进价200元，该店计划用不低于7600元且不高于8000元的资金订购30套甲、乙两款运动服．‎ ‎（1）该店订购这两款运动服，共有哪几种方案？‎ ‎（2）若该店以甲款每套400无，乙款每套300元的价格全部出售，哪种方案获利最大？‎ ‎25．（本题10分）如图1，已知正方形ABCD的边CD在正方形DEFG的边DE上，连接AE、GC．‎ ‎（1）试猜想AE与GC有怎样的位置关系，并证明你的结论．‎ ‎（2）将正方形DEFG绕点D按顺时针方向旋转，使点E落在BC边上，如图2，连接AE和CG。你认为（1）中的结论是否还成立？若成立，给出证明；若不成立，请说明理由．‎ A B G D E ‎（第25题）‎ F C A B G D E F C ‎（图1）‎ ‎（图2）‎ ‎26．在直角梯形OABC中，CB∥OA，∠COA＝90º，CB＝3，OA＝6，BA＝3．分别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系．‎ ‎（1）求点B的坐标；‎ ‎（2）已知D、E分别为线段OC、OB上的点，OD＝5，OE＝2EB，直线DE交x轴于点F．求直线DE的解析式；‎ ‎（3）点M是（2）中直线DE上的一个动点，在x轴上方的平面内是否存在另一个点N．使以O、D、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由．‎ A B D E ‎（第26题 图1）‎ F C O M N x y