中考复习图形的认识与三角形一 11页

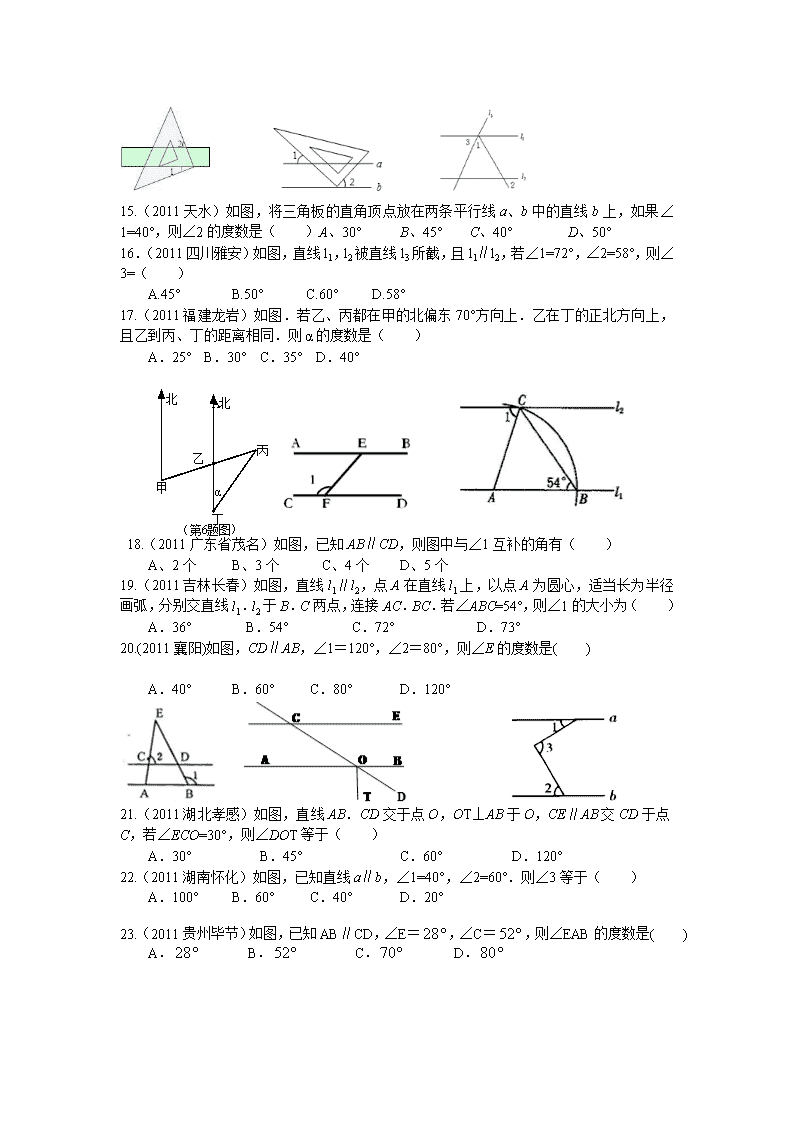
第五章 图形的认识与三角形 课时18．几何初步及平行线、相交线 ‎【知识考点】‎ ‎1. 两点确定一条直线，两点之间 最短，即过两点有且只有一条直线。‎ ‎2. 1周角＝_______，1平角＝_______,1直角＝_______．‎ ‎3. 如果两个角的和等于90度，就说这两个角互余，同角或等角的余角相等；如果_____________________互为补角，__________________的补角相等.‎ ‎4. ___________________________________叫对顶角，对顶角___________.‎ ‎5. 过直线外一点心___________条直线与已知直线平行.‎ ‎6. 平行线的性质：两直线平行，_________相等，________相等，________互补.‎ ‎7. 平行线的判定：________相等,或______相等,或______互补，两直线平行.‎ ‎8. 平面内，过一点有且只有_____条直线与已知直线垂直.‎ ‎9．线段的垂直平分线：‎ ‎ 性质：线段垂直平分线上的到这条线段的 的距离相等；‎ ‎ 判定：到线段 的点在线段的垂直平分线上。‎ ‎10.角的平分线：‎ ‎ 性质：角平分线上的点到角 相等； 判定：到角 的点在这个角的平分线上。‎ ‎【中考试题】‎ 一．选择题 ‎1.（2011年广西桂林）下面四个图形中，∠1=∠2一定成立的是（ ）．‎ ‎2．如图，直线，则的度数是（　 ）‎ ‎(第2题)图 ‎70°‎ ‎31°‎ A． B． C． D．‎ ‎ ‎ ‎3．（2011山东日照）如图，已知直线AB∥CD，∠C=125°，∠A=45°，那么∠E的大小为（　　）‎ ‎ A．70° B．80° C．90° D．100°‎ ‎4.（2011•南通）如图，AB∥CD，∠DCE=80°，则∠BEF=（　　）‎ ‎ A、120° B、110° C、100° D、80°‎ ‎5.（2011山西）如图所示，∠AOB的两边OA、OB均为平面反光镜，∠AOB＝35°在OB上有一点E，从E点射出一束光线经OA上的点D反射后，反射光线DC恰好与OB平行，则∠DEB的度数是（ ）‎ A．35° B． 70° C． 110° D． 120°‎ ‎6.（2011重庆綦江）如图，直线a∥b，AC丄AB，AC交直线b于点C，∠1＝65°，则∠2的度数是（　　）‎ A B D C A．65° B．50° C．35° D．25°‎ ‎7.（2010重庆）如图，AB∥CD，∠C＝80°，∠CAD＝60°，则∠BAD的度数等于( )‎ A．60° B．50° C． 45° D． 40‎ ‎8.（2011•河池）如图，AB∥CD，AC与BD相交于点O，∠A=30°，∠COD=105°．则∠D的大小是（　　）‎ ‎ ‎ ‎ A、30° B、45° C、65° D、75°‎ 9. ‎（2011湖北潜江）如图，AB∥EF∥CD，∠ABC＝46°，∠CEF＝154°，则∠BCE等于（　　 ）‎ A．23° B．16° C．20° D．26°‎ ‎10.（2011•安顺）如图，己知AB∥CD，BE平分∠ABC，∠CDE=150°，则∠C的度数是（　　）‎ ‎ A、100° B、110° C、120° D、150°‎ ‎11.（2011•德州）如图，直线l1∥l2，∠1=40°，∠2=75°，则∠3等于（　　）‎ ‎ ‎ ‎ A、55° B、60° C、65° D、70°‎ ‎12.（2011泰安）如图，l∥m，等腰直角三角形ABC的直角顶点C在直线m上，若∠β＝20°，则∠α的度数为（　　）‎ ‎ A．25° B．30° C．20° D．35°‎ ‎13.（2011四川泸州）如图，∠1与∠2互补，∠3=135°，则∠4的度数是（　　）A.45° B.55° C.65° D.75°‎ 14. 如图，把一块直角三角板的直角顶点放在直尺的一边上，如果∠1=32°，那么∠2的度数是（　　）‎ A、32° B、58° C、68° D、60°‎ ‎ ‎ ‎15.（2011天水）如图，将三角板的直角顶点放在两条平行线a、b中的直线b上，如果∠1=40°，则∠2的度数是（　　）A、30° B、45° C、40° D、50°‎ ‎16．（2011四川雅安）如图，直线l1，l2被直线l3所截，且l1∥l2，若∠1=72°，∠2=58°，则∠3=（　　）‎ ‎ A.45° B.50° C.60° D.58°‎ ‎17.（2011福建龙岩）如图．若乙、丙都在甲的北偏东70°方向上．乙在丁的正北方向上，且乙到丙、丁的距离相同．则α的度数是（ ）‎ ‎ A．25° B．30° C．35° D．40°‎ ‎ ‎ ‎ ‎ ‎18.（2011广东省茂名）如图，已知AB∥CD，则图中与∠1互补的角有（　　）‎ ‎ A、2个 B、3个 C、4个 D、5个 ‎19.（2011吉林长春）如图，直线l1∥l2，点A在直线l1上，以点A为圆心，适当长为半径画弧，分别交直线l1．l2于B．C两点，连接AC．BC．若∠ABC=54°，则∠1的大小为（　　）‎ ‎ A．36° B．54° C．72° D．73°‎ ‎20.(2011襄阳)如图，CD∥AB，∠1＝120°，∠2＝80°，则∠E的度数是(　　)‎ ‎ A．40° B．60° C．80° D．120°‎ ‎ ‎ ‎21.（2011湖北孝感）如图，直线AB．CD交于点O，OT⊥AB于O，CE∥AB交CD于点C，若∠ECO=30°，则∠DOT等于（　　）‎ ‎ A．30° B．45° C．60° D．120°‎ ‎22.（2011湖南怀化）如图，已知直线a∥b，∠1=40°，∠2=60°．则∠3等于（　　）‎ ‎ A．100° B．60° C．40° D．20°‎ ‎23.（2011贵州毕节）如图，已知AB∥CD，∠E＝，∠C＝，则∠EAB的度数是( )‎ ‎ A． B． C． D．‎ ‎ ‎ ‎1‎ ‎2‎ b a 图6‎ c ‎24.（2011广东肇庆）如图，已知直线a∥b∥c，直线m、n与直线a、b、c分别交于点A、C、E、B、D、F，AC=4，CE=6，BD=3，则BF=（　　）‎ ‎ A、7 B、7.5 C、8 D、8.5‎ ‎25..下列说法中正确的有 （ ）‎ ‎①同位角相等；②过一点有且只有一条直线与已知直线平行；‎ ‎③过一点有且只有一条直线与已知直线垂直；④三条直线两两相交总有三个交点；‎ ‎⑤若a∥b,b∥c,则a∥c.‎ A.1个 B.2个 C.3个 D.‎ 二．填空题 ‎1．（2010年，3分）如图6，直线，直线与 相交．若，则．‎ ‎2．(11永州) 如图，直线a、b被直线c所截，若要a∥ b，需增加条件_________．（填一个即可）‎ ‎3. (08宁夏)如图，AB∥CD， AC⊥BC，∠BAC＝65°，则∠BCD度数为____________． ‎ ‎4.（2011云南保山）如图，l1∥l2，∠1=120°，则∠2= .‎ ‎5.（2011江苏）如图，直线a、b被直线c所截，a∥b，∠1=70°，则∠2= .‎ ‎ ‎ ‎6.（2011四川广安）如图所示，直线∥．直线与直线，分别相交于点、点，，垂足为点，若，则＝ _________‎ ‎7.（2011•江西）一块直角三角板放在两平行直线上，如图所示，∠1+∠2=　 　度．‎ ‎ ‎ ‎8.（2011湖州）如图：CD平分∠ACB，DE∥AC且∠1=30°，则∠2=　60　度．‎ ‎9.（2011辽宁本溪）如图：AB∥CD，直线MN分别交AB、CD于点E、F，EG平分∠AEF．EG⊥FG于点G，若∠BEM=50°，则∠CFG= 　 　．‎ ‎ ‎ ‎10.如图，AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，作PE⊥AB于点E．若PE=2，则两平行线AD与BC间的距离为 .‎ 课时19．三角形的有关概念 ‎【知识考点】‎ 一、三角形的分类：‎ ‎1．三角形按角分为______________，______________，_____________．‎ ‎2．三角形按边分为_______________,__________________.‎ 二、三角形的性质：‎ ‎1．三角形中任意两边之和____第三边，两边之差_____第三边 ‎2．三角形的内角和为_______，外角与内角的关系：__________________．‎ 三、三角形中的主要线段：‎ ‎1．___________________________________叫三角形的中位线．‎ ‎2．中位线的性质：____________________________________________．‎ ‎3．三角形三条中位线将三角形分成四个面积相等的全等三角形。‎ ‎4．角平分线：三角形的角平分线交于一点，这点叫三角形的内心，它到三角形三边的距离 ，内心也是三角形内切圆的圆心。‎ ‎5．三角形三边的垂直平分线：三角形三边的垂直平分线交于一点，这点叫做三角形的外心，它到三角形三个顶点的距离 ，外心也是三角形外接圆的圆心。‎ ‎6．三角形的中线、高线、角平分线都是____________．(线段、射线、直线)‎ 四、等腰三角形的性质与判定：‎ ‎1. 等腰三角形的两底角__________；‎ ‎2. 等腰三角形底边上的______、底边上的________和顶角的_______互相重合（三线合一）；‎ ‎3. 有两个角相等的三角形是_________．‎ 五、等边三角形的性质与判定：‎ ‎1. 等边三角形每个角都等于_______，同样具有“三线合一”的性质；‎ ‎2. 三个角相等的三角形是_____，三边相等的三角形是_______，一个角等于60°的_______三角形是等边三角形．‎ 六、直角三角形的性质与判定：‎ ‎1. 直角三角形两锐角________．‎ A B C D ‎40°‎ ‎120°‎ 图1‎ ‎2. 直角三角形中30°所对的直角边等于斜边的________．‎ ‎3. 直角三角形中，斜边的中线等于斜边的______．；‎ ‎4. 勾股定理：_________________________________________．‎ ‎5. 勾股定理的逆定理：_________________________________________________．‎ ‎【中考试题】‎ 一．选择题 ‎1. （2010年，3分）如图1，在△ABC中，D是BC延长线上一点， ∠B = 40°，∠‎ ACD = 120°，则∠A等于（ ）‎ A．60° B．70° ‎ C．80° D．90°‎ ‎2. （2011山东济宁）如果一个等腰三角形的两边长分别是5cm和6cm，那么此三角形的周长是 ‎ A．15cm B．16cm ‎ C．17cm D．16cm或17cm ‎3. （2011四川）如图，在中，，，点为的中点，，垂足为点，则等于（　　） ‎ A．　　 B． 　　C．　　 D． ‎‎（第7题）‎ ‎ ‎ ‎4. （2011浙江省舟山）如图，边长为4的等边△ABC中，DE为中位线，则四边形BCED的面积为（　 　）‎ ‎（A） （B） （C） （D）‎ ‎5. （2011山东德州13,4分）下列命题中，其逆命题成立的是______________．（只填写序号）‎ ‎①同旁内角互补，两直线平行；‎ ‎②如果两个角是直角，那么它们相等；‎ ‎③如果两个实数相等，那么它们的平方相等；‎ ‎④如果三角形的三边长a，b，c满足，那么这个三角形是直角三角形．‎ ‎6. （2011四川南充市）如图，⊿ABC和⊿CDE均为等腰直角三角形，点B,C,D在一条直线上，点M是AE的中点，下列结论：①tan∠AEC=;②S⊿ABC+S⊿CDE≧S⊿ACE ;③BM⊥DM;④BM=DM.正确结论的个数是（ ） （A）1个 （B）2个 （C）3个 （D）4个 二、填空题 ‎1. （2011山东滨州）边长为6cm的等边三角形中，其一边上高的长度为________.‎ ‎2.（2011山东）等腰三角形的周长为14，其一边长为4，那么，它的底边为 .‎ ‎3．等腰两边的长分别是一元二次方程的两个解，则这个等腰三角形的周长是 ．‎ ‎4. （2011湖南邵阳）如图（四）所示，在△ABC中，AB=AC，∠B=50°，则∠A=_______。‎ ‎ ‎ ‎5. （2011湖南怀化）如图6，在△ABC中，AB=AC，∠BAC的角平分线交BC边于点D，AB=5，BC=6，则AD=__________________.‎ ‎6. （2011贵州安顺，16，4分）如图，在Rt△ABC中，∠C=90°，BC=6cm，AC=8cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB边的C′点，那么△ADC′的面积是 ．‎ 第6题图 ‎7. （2011河北）如图3，在△ABC中，∠C=90°，BC=6,D,E分别在AB,AC上，将△ABC沿DE折叠，使点A落在点A′处，若A′为CE的中点，则折痕DE的长为（ ）‎ A． B．2 C．3 D．4 ‎ 二填空题 ‎8. (2011重庆綦江) 一个正方体物体沿斜坡向下滑动，其截面如图所示.正方形DEFH的边长为2米，坡角∠A＝30°,∠B＝90°,BC＝6米. 当正方形DEFH运动到什么位置,即当AE＝ 米时,有DC＝AE＋BC. ‎ ‎9. （2011浙江台州）已知等边△ABC中，点D,E分别在边AB,BC上，把△BDE沿直线DE翻折，使点B落在点Bˊ处，DBˊ,‎ EBˊ分别交边AC于点F，G，若∠ADF=80º ，则∠EGC的度数为 ‎ ‎10. （2011浙江）如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°四边形ACDE是平行四边形，连结CE交AD于点F，连结BD交 ‎ CE于点G，连结BE. 下列结论中：‎ ‎① CE=BD； ② △ADC是等腰直角三角形；‎ ‎③ ∠ADB=∠AEB； ④ CD·AE=EF·CG；一定正确的结论有 .‎A B C D E F G ‎11.如图7-67所示,有一底角为35°的等腰三角形纸片,现过底边上 一点,沿与底边垂直的方向将其剪开,分成三角形和四边形两部分,则四边形中的最大角的度数是______.‎ ‎12. （2011广东茂名，14，3分）如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG＝CD，DF＝DE，则∠E＝ 度．‎ ‎ ‎ ‎13. （2011贵州贵阳）如图，已知等腰Rt△ABC的直角边长为1，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推直到第五个等腰Rt△AFG，则由这五个等腰直角三角形所构成的图形的面积为______．‎ ‎14. （2011四川乐山）如图，已知∠AOB=，在射线OA、OB上分别取点OA=OB，连结AB，在BA、BB上分别取点A、B，使B B= B A，连结A B…按此规律上去，记∠A B B=，∠，…，∠‎ 则⑴= ； ⑵ = 。‎ 三解答题 ‎15. （2011湖北襄阳，21，6分）‎ 如图6，点D，E在△ABC的边BC上，连接AD，AE. ①AB＝AC；②AD＝AE；③BD＝CE.以此三个等式中的两个作为命题的题设，另一个作为命题的结论，构成三个命题：①②③；①③②；②③①.‎ ‎（1）以上三个命题是真命题的为（直接作答） ；‎ ‎（2）请选择一个真命题进行证明（先写出所选命题，然后证明）.‎ 图6‎ ‎16.　已知等腰三角形一腰上的中线把这个三角形的周长分为13 cm和15 cm两部分，试求此等腰三角形的腰长和底边长．‎ ‎17.（2011•青海）认真阅读下面关于三角形内外角平分线所夹的探究片段，完成所提出的问题．‎ 探究1：如图1，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90°+，理由如下：‎ ‎∵BO和CO分别是∠ABC和∠ACB的角平分线 ‎∴‎ ‎∴‎ 又∵∠ABC+∠ACB=180°﹣∠A ‎∴‎ ‎∴∠BOC=180°﹣（∠1+∠2）=180°﹣（90°﹣∠A）=‎ 探究2：如图2中，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由．‎ 探究3：如图3中，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？（只写结论，不需证明）‎ 结论：　 　．‎ ‎18. （2011年，10分）在图14-1至图14-3中，点B是线段AC的中点，点D是线段CE的中点．四边形BCGF和CDHN都是正方形．AE的中点是M．‎ ‎（1）如图14-1，点E在AC的延长线上，点N与点G重合时，点M与点C重合，‎ 求证：FM = MH，FM⊥MH；‎ 图14-1‎ A H C(M)‎ D E B F G(N)‎ G 图14-2‎ A H C D E B F N M A H C D E 图14-3‎ B F G M N ‎（2）将图14-1中的CE绕点C顺时针旋转一个锐角，得到图14-2，‎ 求证：△FMH是等腰直角三角形；‎ ‎（3）将图14-2中的CE缩短到图14-3的情况，‎ ‎△FMH还是等腰直角三角形吗？（不必 说明理由）‎ ‎19. （2011四川乐山25，12分）如图,在直角△ABC中, ∠ACB=90,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F,若AC=mBC,CE=nEA(m,n为实数).试探究线段EF与EG的数量关系.‎ ‎ ‎ (1) 如图(14.2),当m=1,n=1时,EF与EG的数量关系是 ‎ 证明:‎ (2) ‎ 如图(14.3),当m=1,n为任意实数时,EF与EG的数量关系是 ‎ 证明 (3) 如图(14.1),当m,n均为任意实数时,EF与EG的数量关系是 ‎ ‎(写出关系式,不必证明)‎ ‎20. (2011浙江绍兴，23，12分)数学课上，李老师出示了如下框中的题目.‎ 小敏与同桌小聪讨论后，进行了如下解答：‎ ‎（1）特殊情况，探索结论 当点为的中点时，如图1，确定线段与的大小关系，请你直接写出结论：‎ ‎ （填“>”,“<”或“=”）. ‎ 第25题图2‎ 第25题图1‎ ‎（2）特例启发，解答题目 解：题目中，与的大小关系是： （填“>”,“<”或“=”）.理由如下：如图2，过点作，交于点.‎ ‎（请你完成以下解答过程）‎ ‎（3）拓展结论，设计新题 在等边三角形中，点在直线上，点在直线上，且.若的边长为1，，求的长（请你直接写出结果）. ‎