中考数学面积问题压轴题 6页

‎§2.2　由面积产生的函数关系问题 图形运动的过程中,求面积随某个量变化的函数关系,是中考数学的热点问题.‎ 计算面积常见的有四种方法,一是规则图形的面积用面积公式;二是不规则图形的面积通过割补进行计算;三是同高(或同底)三角形的面积比等于对应边(或高)的比;四是相似三角形的面积比等于相似比的平方.‎ 前两种方法容易想到,但是灵活使用第三种和第四种方法,可以使得运算简单.‎ 一般情况下,在求出面积S关于自变量x的函数关系后,会提出在什么情况下(x为何值时),S取得最大值或最小值.‎ 关于面积的最值问题,有许多经典的结论.‎ ‎1. 周长一定的矩形,当正方形时,面积最大.‎ ‎2. 面积一定的矩形,当正方形时,周长最小.‎ ‎3. 周长一定的正多边形,当边数越大时,面积越大,极限值是圆.‎ ‎4. 如图1,锐角△ABC的内接矩形DEFG的面积为y, AD=x,当点D是AB的中点时,面积y最大.‎ ‎5. 如图2,点P在直线AB上方的抛物线上一点,当点P位于AB的中点E的正上方时,△PAB的面积最大.‎ ‎6. 如图3,△ABC中,∠A和对边BC是确定的,当AB=AC时,△ABC的面积最大.‎ ‎ 图1‎ ‎ ‎ ‎ 图2 图3 ‎ 例8　2016年淮安市中考第27题 如图所示,在平面直角坐标系中,二次函数y=-‎1‎‎4‎x2+bx+c的图象与坐标轴交于A、 B、 C三点,其中点A的坐标为(0, 8),点B的坐标为(-4, 0).‎ ‎(1) 求该二次函数的表达式及点C的坐标;‎ ‎(2) 点D的坐标为(0, 4),点F为该二次函数在第一象限内图象上的动点,连结CD、 CF,以CD、 CF为邻边作平行四边形CDEF.设平行四边形CDEF的面积为S.‎ ‎① 求S的最大值;‎ ‎② 在点F的运动过程中,当点E落在该二次函数的图象上时,请直接写出此时S的值.‎ 请打开几何画板文件名“16淮安27”,拖动点F在第一象限内的抛物线上运动,观察△CDF的面积随点F变化的函数图象,可以体验到,当点F的横坐标为3时,△CDF的面积最大;当点F的横坐标为7时,点E落在抛物线上.‎ ‎1. 把点F的横坐标x设为自变量,用x表示△CDF的面积.‎ ‎2. 连结OF“割补”△CDF比较简便.‎ ‎3. 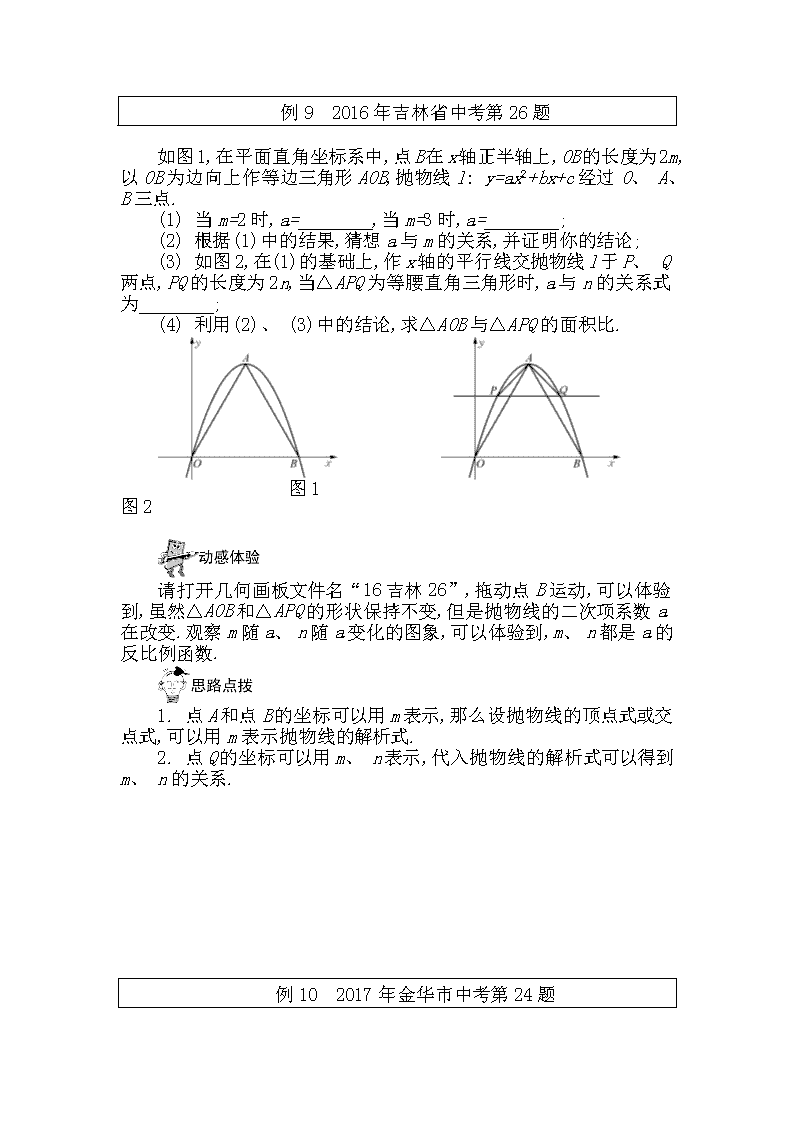如果设点F的坐标为(m, n),根据FE与CD平行且相等,通过坐标平移可以表示点E的坐标,再把点F、 E的坐标分别代入抛物线的解析式,联立方程组求m的值.‎ 例9　2016年吉林省中考第26题 如图1,在平面直角坐标系中,点B在x轴正半轴上,OB的长度为2m,以OB为边向上作等边三角形AOB,抛物线l: y=ax2+bx+c经过O、 A、 B三点.‎ ‎(1) 当m=2时,a=　　　　,当m=3时,a=　　　　; ‎ ‎(2) 根据(1)中的结果,猜想a与m的关系,并证明你的结论;‎ ‎(3) 如图2,在(1)的基础上,作x轴的平行线交抛物线l于P、 Q两点,PQ的长度为2n,当△APQ为等腰直角三角形时,a与n的关系式为　　　　; ‎ ‎(4) 利用(2)、 (3)中的结论,求△AOB与△APQ的面积比.‎ ‎ ‎ ‎ 图1 图2‎ 请打开几何画板文件名“16吉林26”,拖动点B运动,可以体验到,虽然△AOB和△APQ的形状保持不变,但是抛物线的二次项系数a在改变.观察m随a、 n随a变化的图象,可以体验到,m、 n都是a的反比例函数.‎ ‎1. 点A和点B的坐标可以用m表示,那么设抛物线的顶点式或交点式,可以用m表示抛物线的解析式.‎ ‎2. 点Q的坐标可以用m、 n表示,代入抛物线的解析式可以得到m、 n的关系.‎ 例10　2017年金华市中考第24题 如图1,四边形OABC各顶点的坐标分别为O(0, 0), A(3, 3‎3‎), B(9, 5‎3‎), C(14, 0).动点P与Q同时从点O出发,运动时间为t秒,点P沿OC方向以1个单位/秒的速度向点C运动,点Q沿折线OA—AB—BC运动,在OA、 AB、 BC上运动的速度分别为3、 ‎3‎、 ‎5‎‎2‎(单位长度/秒).当P、 Q中的一点到达点C时,两点同时停止运动.‎ ‎(1) 求AB所在直线的函数表达式;‎ ‎(2) 如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值;‎ ‎(3) 在P、 Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t的值.‎ ‎ ‎ ‎ 图1 图2‎ 请打开几何画板文件名“17金华24”,拖动点P运动,可以体验到,PQ的垂直平分线4次经过四边形OABC的顶点.‎ ‎1. 先求线段OA、 AB、 BC的长,把点Q在三条线段上的运动时间罗列出来.‎ ‎2. 直线OA、 BC与x轴的夹角为60°,直线AB与x轴的夹角为30°.‎ ‎3. 点Q在AB上时,AQ=速度×时间=‎3‎(t-2).‎ 点Q在BC上时,BQ=速度×时间=‎5‎‎2‎(t-6), CQ=‎5‎‎2‎(10-t).‎ 例11　2017年黄冈市中考第24题 如图,在平面直角坐标系中,四边形OABC是矩形,OA=4, OC=3.动点P从点C出发,沿射线CB方向以每秒2个单位长度的速度运动;同时,动点Q从点O出发,沿x轴正半轴方向以每秒1个单位长度的速度运动.设点P、 Q的运动时间为t秒.‎ ‎(1) 当t=1秒时,求经过O、 P、 A三点的抛物线的解析式;‎ ‎(2) 当t=2秒时,求tan∠QPA的值;‎ ‎(3) 当线段PQ与线段AB相交于点M,且BM=2AM时,求t的值;‎ ‎(4) 连结CQ,当点P、 Q在运动过程中,记△CQP与矩形OABC重叠部分的面积为S,求S与t的函数关系式.‎ 请打开几何画板文件名“17黄冈24”,拖动点Q由点O向右运动,可以体验到,△CQP与矩形OABC重叠部分的形状依次是△CQP、四边形CQMB和△CBN.‎ ‎1. 第(1)题:设交点式比较简便,代入点P的坐标求二次项系数a就好了.‎ ‎2. 第(2)题:点P恰好与点B重合,∠QPA就在直角三角形中.‎ ‎3. 第(3)题:根据“8字型”相似列方程,为第(4)题提供方法依据.‎ ‎4. 第(4)题:分三种情况讨论.‎ 例12　2017年绵阳市中考第25题 如图,已知△ABC中,∠C=90°,点M从点C出发沿CB方向以1cm/s的速度匀速运动,到达点B停止运动.在点M的运动过程中,过点M作直线MN交AC于点N,且保持∠NMC=45°,再过点N作AC的垂线交AB 于点F,连结MF.将△MNF关于直线NF对称后得到△ENF.已知AC=8cm, BC=4cm.设点M的运动时间为t(s), △ENF与△ANF重叠部分的面积为y(cm2).‎ ‎(1) 在点M的运动过程中,能否使得四边形MNEF为正方形?如果能,求出相应的t值;如果不能,说明理由;‎ ‎(2) 求y关于t的函数解析式及相应的t的取值范围;‎ ‎(3) 当y取得最大值时,求sin∠NEF的值.‎ 请打开几何画板文件名“17绵阳25”,拖动点M运动,观察y随t变化的函数图象,可以体验到,当重叠部分的面积最大时,点E恰好落在AB的中点.‎ ‎1. 用含t的式子可以把线段CM、 CN、 BM、 FN的长都表示出来.‎ ‎2. △MNC和△MNE保持等腰直角三角形的形状,MN、 EN、 EM也可以用t表示.‎ ‎3. 当EN与AB交于点D时,可以用t表示出高DG.‎