2018中考数学专题复习全等三角形压轴题分类解析无答案 5页

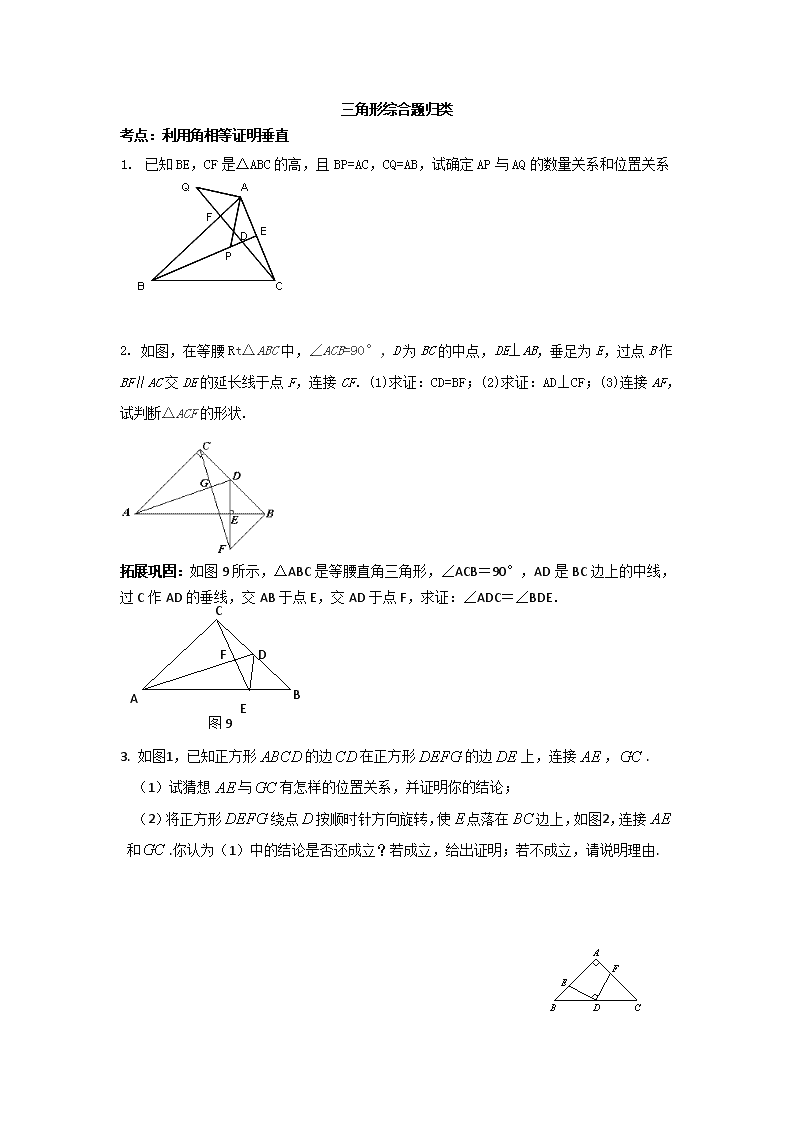
三角形综合题归类 考点：利用角相等证明垂直 1. 已知BE，CF是△ABC的高，且BP=AC，CQ=AB，试确定AP与AQ的数量关系和位置关系 ‎2. 如图，在等腰Rt△ABC中，∠ACB=90°，D为BC的中点，DE⊥AB，垂足为E，过点B作BF∥AC交DE的延长线于点F，连接CF．(1)求证：CD=BF；(2)求证：AD⊥CF；(3)连接AF，试判断△ACF的形状.‎ A B C D E F 图9‎ 拓展巩固：如图9所示，△ABC是等腰直角三角形，∠ACB＝90°，AD是BC边上的中线，过C作AD的垂线，交AB于点E，交AD于点F，求证：∠ADC＝∠BDE．‎ ‎3. 如图1，已知正方形的边在正方形的边上，连接，. （1）试猜想与有怎样的位置关系，并证明你的结论；‎ ‎（2）将正方形绕点按顺时针方向旋转，使点落在边上，如图2，连接和.你认为（1）中的结论是否还成立？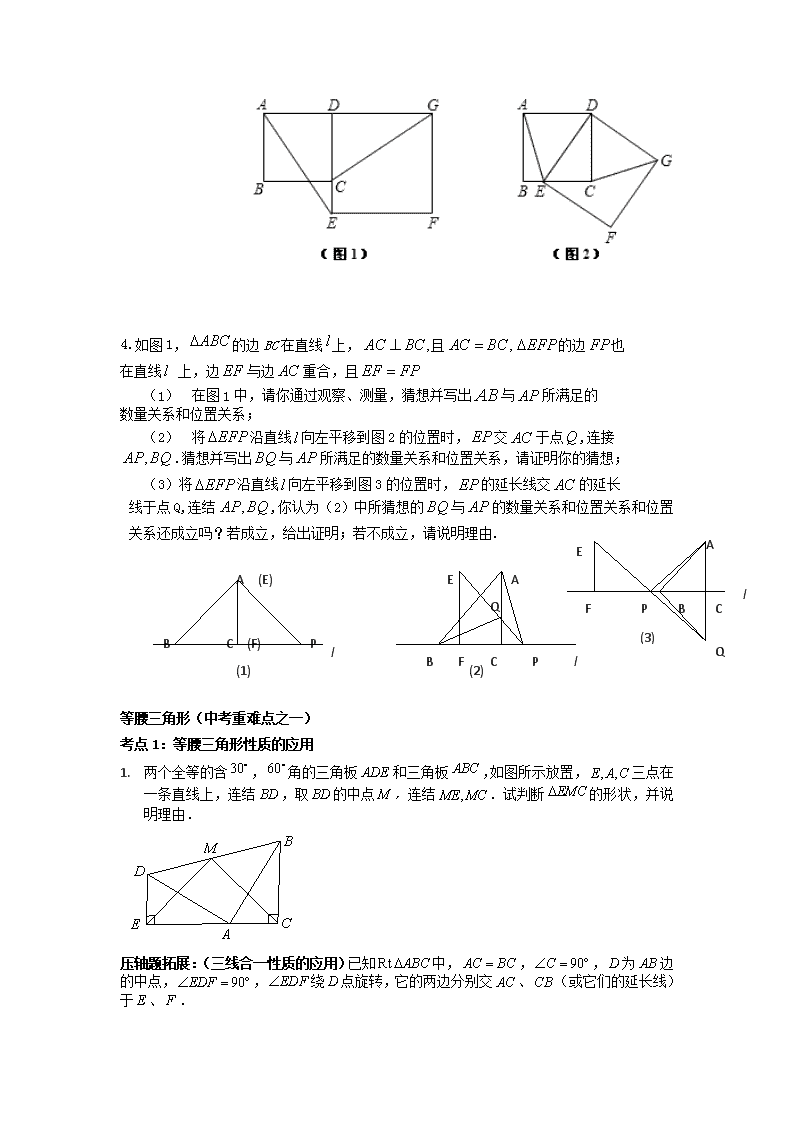若成立，给出证明；若不成立，请说明理由.‎ ‎4.如图1，的边BC在直线上，且的边也 在直线 上，边与边重合，且 （1） 在图1中，请你通过观察、测量，猜想并写出与所满足的 数量关系和位置关系；‎ （2） 将沿直线向左平移到图2的位置时，交于点,连接 ‎.猜想并写出与所满足的数量关系和位置关系，请证明你的猜想；‎ ‎（3）将沿直线向左平移到图3的位置时，的延长线交的延长 A B E C F P l ‎(3)‎ Q 线于点Q,连结,你认为（2）中所猜想的与的数量关系和位置关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由. ‎ l ‎(1)‎ A B ‎(F)‎ ‎(E)‎ C P A B E C F P Q ‎(2)‎ l 等腰三角形（中考重难点之一）‎ 考点1：等腰三角形性质的应用 1. 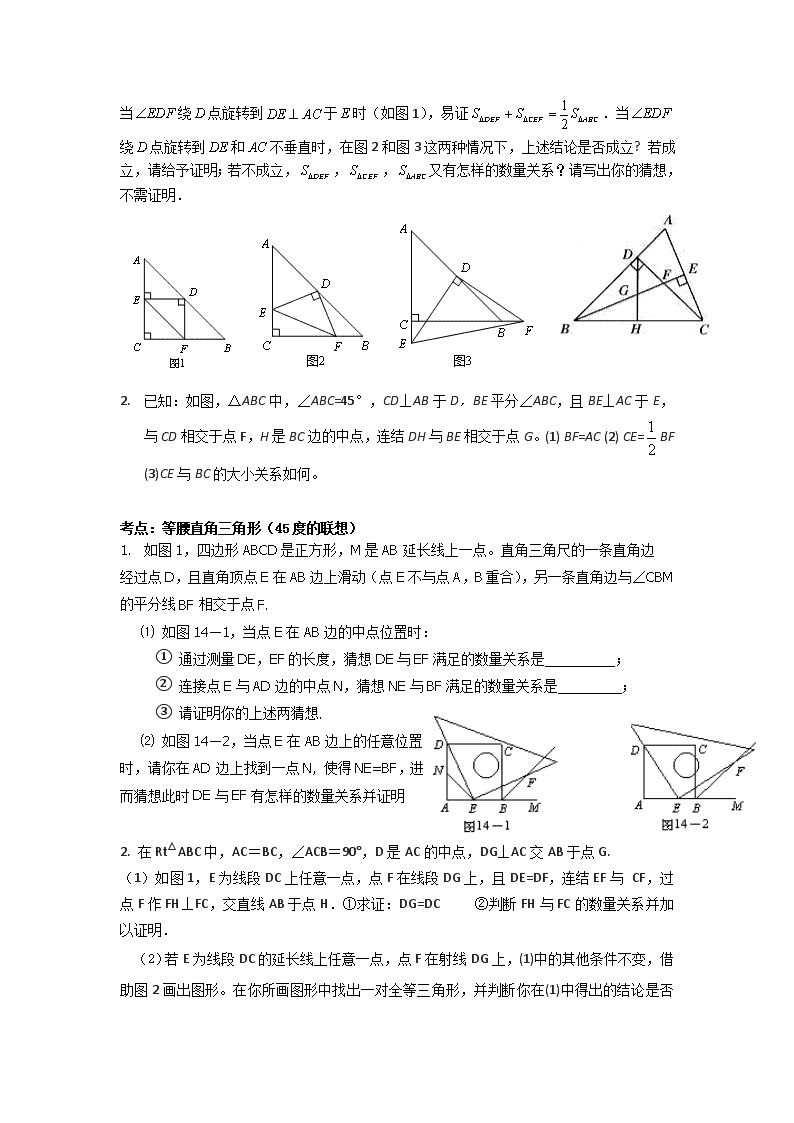两个全等的含，角的三角板和三角板，如图所示放置，三点在一条直线上，连结，取的中点，连结．试判断的形状，并说明理由．‎ 压轴题拓展：（三线合一性质的应用）已知中，，，为边的中点，，绕点旋转，它的两边分别交、（或它们的延长线）于、．‎ 当绕点旋转到于时（如图1），易证．当绕点旋转到和不垂直时，在图2和图3这两种情况下，上述结论是否成立? 若成立，请给予证明；若不成立，，，又有怎样的数量关系？请写出你的猜想，不需证明．‎ 1. 已知：如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连结DH与BE相交于点G。(1) BF=AC (2) CE=BF (3)CE与BC的大小关系如何。‎ 考点：等腰直角三角形（45度的联想）‎ 1. 如图1，四边形ABCD是正方形，M是AB延长线上一点。直角三角尺的一条直角边 经过点D，且直角顶点E在AB边上滑动（点E不与点A，B重合），另一条直角边与∠CBM 的平分线BF相交于点F.‎ ‎⑴ 如图14―1，当点E在AB边的中点位置时：‎ ‎① 通过测量DE，EF的长度，猜想DE与EF满足的数量关系是 ；‎ ‎② 连接点E与AD边的中点N，猜想NE与BF满足的数量关系是 ；‎ ‎③ 请证明你的上述两猜想.‎ ‎⑵ 如图14―2，当点E在AB边上的任意位置时，请你在AD边上找到一点N, 使得NE=BF，进而猜想此时DE与EF有怎样的数量关系并证明 ‎2. 在Rt△ABC中，AC＝BC，∠ACB＝90°，D是AC的中点，DG⊥AC交AB于点G.‎ ‎（1）如图1，E为线段DC上任意一点，点F在线段DG上，且DE=DF，连结EF与 CF，过点F作FH⊥FC，交直线AB于点H．①求证：DG=DC ②判断FH与FC的数量关系并加以证明．‎ ‎（2）若E为线段DC的延长线上任意一点，点F在射线DG上，(1)中的其他条件不变，借助图2画出图形。在你所画图形中找出一对全等三角形，并判断你在 ‎(1)中得出的结论是否发生改变．（直接写出结论，不必证明）‎ 图1‎ 图2‎ 同类变式： 已知：△ABC为等边三角形，M是BC延长线上一点，直角三角尺的一条直角边经过点A，且60º角的顶点E在BC上滑动，（点E不与点B、C重合），斜边与∠ACM的平分线CF交于点F ‎（1）如图（1）当点E在BC边得中点位置时 ‎ 猜想AE与EF满足的数量关系是 .‎ ‎ 连结点E与ＡＢ边得中点Ｎ，猜想ＢＥ和ＣＦ满足的数量关系是　　　.‎ 请证明你的上述猜想；‎ ‎（２）如图（２）当点Ｅ在ＢＣ边得任意位置时，ＡＥ和EF有怎样的数量关系，并说明你的理由？‎ ‎ ‎ 附加思考题： 以的两边、为腰分别向外作等腰和等腰，.连接，、分别是、的中点．探究：与的位置关系及数量关系．‎ ‎⑴如图① 当为直角三角形时，与的位置关系是 ；线段与的数量关系是 ；‎ ‎⑵将图①中的等腰绕点沿逆时针方向旋转()后，如图②所示，⑴问中得到的两个结论是否发生改变？并说明理由．‎ ‎ ‎ ‎24、已知：如图，矩形中点为延长线上一点，连接，且，点分别在上，且。（1）若，求的长；‎ ‎（2）若，求证：。‎ ‎12、（2010年宁德市）（本题满分13分）如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.‎ ‎⑴ 求证：△AMB≌△ENB；⑵ ①当M点在何处时，AM＋CM的值最小；‎ ‎②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；‎ E A D B C N M ‎⑶ 当AM＋BM＋CM的最小值为时，求正方形的边长.‎ ‎28．如图甲，已知∠ABC=90°，△ABD是边长为2的等边三角形，点E为射线BC上任意一点（点E与点B不重合），连结AE，在AE的上方作等边三角形AEF，连结FD并延长交射线BC于点G．‎ ‎（1）如图乙，当BE=BA时，求证：△ABE≌△ADF；‎ ‎（2）如图甲，当△AEF与△ABD不重叠时，求∠FGC的度数；‎ ‎（3）若将已知条件中的“在AE的上方作等边三角形AEF，连结FD并延长交射线BC于点G．”改为“在AE的下方作等边三角形AEF，连结FD交射线BC于点G．”（如图丙所示），试问当点E在何处时BD∥EF？并求此时△AEF的周长．‎ 图甲 A C B D F G E 图乙 A B D F E G C 图丙 F G A C B D E