湖州中考数学试题 10页

二00八年浙江省初中毕业生学业考试（湖州市）数学试卷 友情提示：‎ ‎1．全卷分卷Ⅰ和卷Ⅱ两部分，共8页．考试时间为100分钟．‎ ‎2．第四题为自选题，供考生选做，本题分数将计入本学科的总分，但考生所得总分最多为120分．‎ ‎3．卷Ⅰ中试题（第1－12小题）的答案填涂在答题卡上，写在试卷上无效．‎ ‎4．请仔细审题，细心答题，相信你一定会有出色的表现！‎ ‎5．参考公式：抛物线y=ax2+bx+c的顶点坐标是．‎ 卷Ⅰ 一、选择题（本题有12小题，每小题3分，共36分）‎ 下面每小题给出的四个选项中，只有一个是正确的．请选出各题中一个最符合题意的选项，并在答题卡上将相应题次中对应字母的方框涂黑，不选、多选、错选均不给分．‎ ‎1．2的相反数是（ ）‎ A． B． C． D．‎ ‎2．当时，代数式的值是（ ）‎ A． B． C． D，‎ ‎3．数据2，4，4，5，3的众数是（ ）‎ A．2 B．3 C．4 D．5‎ ‎4．已知，则的余角的度数是（ ）‎ A． B． C． D．‎ ‎5．计算所得的结果是（ ）‎ A． B． C． D．‎ ‎6．一个布袋里装有3个红球、2个白球，每个球除颜色外均相同，从中任意摸出一个球，则摸出的球是红球的概率是（ ）‎ A． B． C． D．‎ ‎7．已知两圆的半径分别为3cm和2cm，圆心距为5cm，则两圆的位置关系是（ ）‎ A．外离 B．外切 C．相交 D．内切 ‎8．下列各数中，可以用来证明命题“任何偶数都是8的整数倍”是假命题的反例是（ ）‎ A．32 B．16 C．8 D．4‎ ‎9．如图，已知圆心角，则圆周角的度数是（ ）‎ A． B． C． D．‎ ‎10．如图，已知直角三角形中，斜边的长为，，则直角边的长是（ ）‎ A． B． C． D．‎ ‎11．解放军某部接到上级命令，乘车前往四川地震灾区抗震救灾．前进一段路程后，由于道路受阻，汽车无法通行，部队通过短暂休整后决定步行前往．若部队离开驻地的时间为（小时），离开驻地的距离为（千米），则能反映与之间函数关系的大致图象是（ ）‎ ‎12．已知点的坐标为，为坐标原点，连结，将线段绕点按逆时针方向旋转得，则点的坐标为（ ）‎ A． B． C． D．‎ 卷Ⅱ 二、填空题（本题有6小题，每小题4分，共24分）‎ ‎13．计算： ．‎ ‎14．已知等腰三角形的一个底角为，则它的顶角为 度．‎ ‎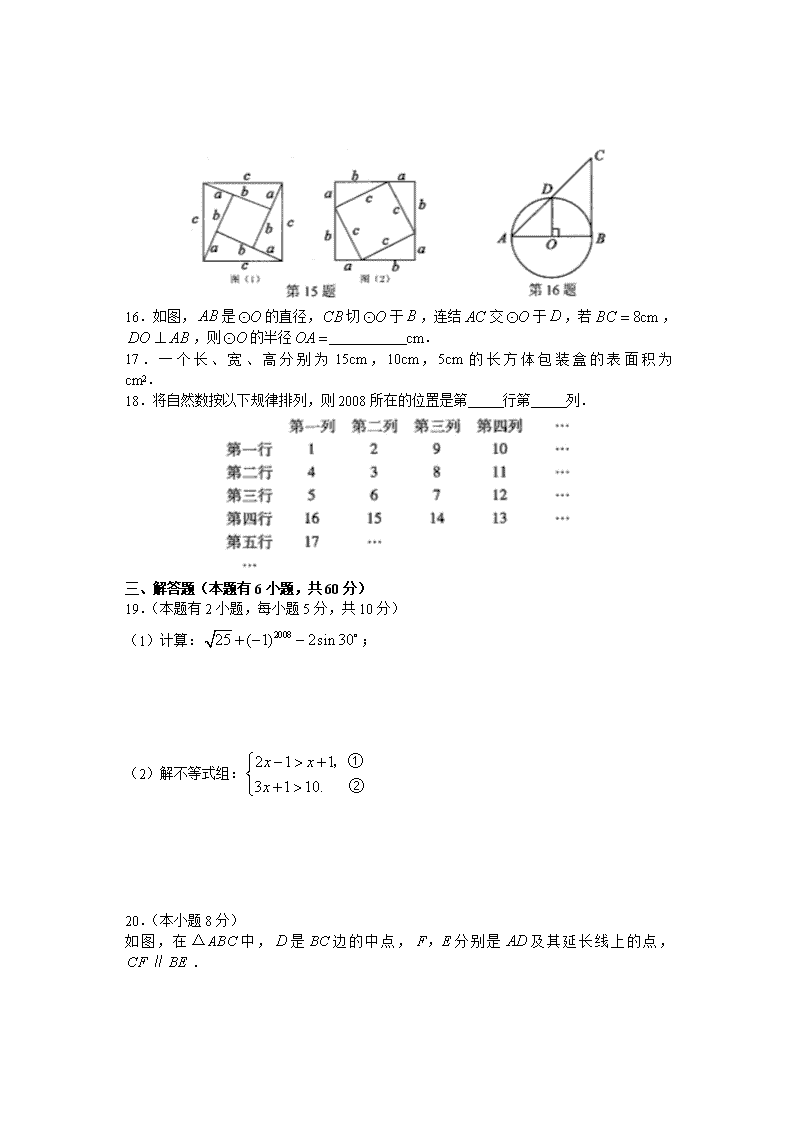15．利用图（1）或图（2）两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理，这个定理称为 ，该定理的结论其数学表达式是 ．‎ ‎16．如图，是的直径，切于，连结交于，若，，则的半径 cm．‎ ‎17．一个长、宽、高分别为15cm，10cm，5cm的长方体包装盒的表面积为 cm2．‎ ‎18．将自然数按以下规律排列，则2008所在的位置是第 行第 列．‎ 三、解答题（本题有6小题，共60分）‎ ‎19．（本题有2小题，每小题5分，共10分）‎ ‎（1）计算：；‎ ‎（2）解不等式组：‎ ‎20．（本小题8分）‎ 如图，在中，是边的中点，分别是及其延长线上的点，．‎ ‎（1）求证：．‎ ‎（2）请连结，试判断四边形是何种特殊四边形，并说明理由．‎ ‎21．（本小题10分）‎ 为了解九年级学生每周的课外阅读情况，某校语文组调查了该校九年级部分学生某周的课外阅读量（精确到千字），将调查数据经过统计整理后，得到如下频数分布直方图．请根据该频数分布直方图，回答下列问题：‎ ‎（1）填空：‎ ‎①该校语文组调查了 名学生的课外阅读量；‎ ‎②左边第一组的频数＝ ，频率＝ ．‎ ‎（2）求阅读量在14千字及以上的人数．‎ ‎（3）估计被调查学生这一周的平均阅读量（精确到千字）．‎ ‎22．（本小题10分）‎ 为了支援四川人民抗震救灾，某休闲用品有限公司主动承担了为灾区生产2万顶帐篷的任务，计划10天完成．‎ ‎（1）按此计划，该公司平均每天应生产帐篷 顶；‎ ‎（2）生产2天后，公司又从其它部门抽调了50名工人参加帐篷生产，同时，通过技术革新等手段使每位工人的工作效率比原计划提高了，结果提前2天完成了生产任务．求该公司原计划安排多少名工人生产帐篷？‎ ‎23．（本小题10分）‎ 如图甲，在等腰直角三角形中，，点在第一象限，点坐标为．与关于轴对称．‎ ‎（1）求经过三点的抛物线的解析式；‎ ‎（2）若将向上平移个单位至（如图乙），则经过三点的抛物线的对称轴在轴的 ．（填“左侧”或“右侧”）‎ ‎（3）在（2）的条件下，设过三点的抛物线的对称轴为直线．求当为何值时，？‎ ‎24．（本小题12分）‎ 已知：在矩形中，，．分别以所在直线为轴和 轴，建立如图所示的平面直角坐标系．是边上的一个动点（不与重合），过点的反比例函数的图象与边交于点．‎ ‎（1）求证：与的面积相等；‎ ‎（2）记，求当为何值时，有最大值，最大值为多少？‎ ‎（3）请探索：是否存在这样的点，使得将沿对折后，点恰好落在上？若存在，求出点的坐标；若不存在，请说明理由．‎ 四、自选题（本题5分）‎ 请注意：本题为自选题，供考生选做．自选题得分将计入本学科总分，但考试总分最多为120分．‎ ‎25．对于二次函数，如果当取任意整数时，函数值都是整数，那么我们把该函数的图象叫做整点抛物线（例如：）．‎ ‎（1）请你写出一个二次项系数的绝对值小于1的整点抛物线的解析式 ．（不必证明）‎ ‎（2）请探索：是否存在二次项系数的绝对值小于的整点抛物线？若存在，请写出其中一条抛物线的解析式；若不存在，请说明理由．‎ 浙江省2008年初中毕业生学业考试（湖州市）‎ 数学试卷参考答案 一、选择题（每小题3分，共36分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A B C A A C B D C B A C 二、填空题（每小题4分，共24分）‎ ‎13．1 14．40 15．勾股定理， 16．4‎ ‎17．550 18．18，45‎ 三、解答题（共60分）‎ ‎19．（本题有2小题，每小题5分，共10分）‎ ‎（1）解：原式 ‎（2）解：由①得 由②得 所以不等式组的解集为．‎ ‎20．（本小题8分）‎ ‎（1）证明：，．‎ 又，，‎ ‎．‎ ‎（2）四边形是平行四边形．‎ 由，得．‎ ‎，四边形是平行四边形．‎ ‎21．（本小题10分）‎ ‎（1）①40；②4，0.1（每答对一个得2分）‎ ‎（2）由图知，阅读量在14千字及以上的学生人数为人．‎ ‎（3）估计被调查学生这一周的平均阅读量为：‎ ‎（千字）．‎ 答：被调查学生这一周的平均阅读量约为13千字．‎ ‎22．（本小题10分）‎ 解：（1）2000‎ ‎（2）设该公司原计划安排名工人生产帐篷，则由题意得：‎ ‎，‎ ‎．‎ 解这个方程，得．‎ 经检验，是所列方程的根，且符合题意．‎ 答：该公司原计划安排750名工人生产帐篷．‎ ‎23．（本小题10分）‎ 解：（1）由题意可知：经过三点的抛物线的顶点是原点，‎ 故可设所求抛物线的解析式为．‎ ‎，点坐标为．……‎ 在抛物线上，，…，‎ 经过三点的抛物线解析式是．‎ ‎（2）左侧．‎ ‎（3）由题意得：点的坐标为，‎ 抛物线过原点，故可设抛物线解析式为，‎ 抛物线经过点和点，‎ ‎ 得，．‎ 抛物线对称轴必在轴的左侧，，而，，‎ ‎，．‎ 即当时，．‎ ‎24．（本小题12分）‎ ‎（1）证明：设，，与的面积分别为，，‎ 由题意得，．‎ ‎，．‎ ‎，即与的面积相等．‎ ‎（2）由题意知：两点坐标分别为，，‎ ‎，‎ ‎．‎ 当时，有最大值．‎ ‎．‎ ‎（3）解：设存在这样的点，将沿对折后，点恰好落在边上的点，过点作，垂足为．‎ 由题意得：，，，‎ ‎，．‎ 又，‎ ‎．‎ ‎，，‎ ‎．‎ ‎，，解得．‎ ‎．‎ 存在符合条件的点，它的坐标为．‎ 四、自选题（共5分）‎ ‎25．（1）如：，等等 ‎（只要写出一个符合条件的函数解析式）‎ ‎（2）解：假设存在符合条件的抛物线，则对于抛物线 当时，当时，‎ 由整点抛物线定义知：为整数，为整数，‎ 必为整数．‎ 又当时，是整数，‎ 必为整数，从而应为的整数倍，‎ ‎，‎ ‎．‎ 不存在二次项系数的绝对值小于的整点抛物线．‎