中考数学压轴题难题破解策略讲义 4页

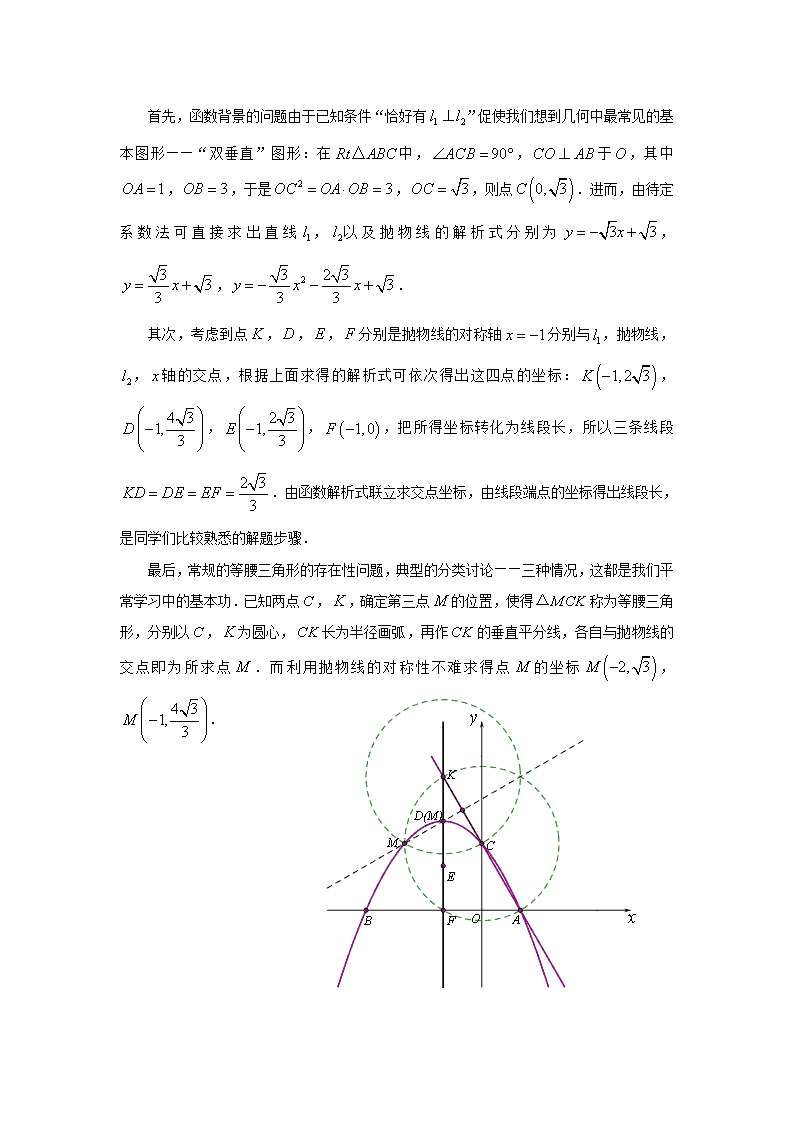
第二讲：“未雨绸缪”应挑战 ‎——中考数学难题破解策略 我们都知道，在学习数学的过程中，所积累的知识、经验经过加工，会得出具有长久保存价值或基本重要性的典型结构与重要类型——数学模型，利用数学模型去解决新问题，是破解中考数学难题的一个非常重要的策略．而这一策略的重要体现往往是“熟悉化原则”和“简单化原则”——将综合题化陌生为熟悉或者分解为若干个基本问题，因而要想掌握好这一解题策略，就得多多积累“基本问题”．当我们具有了一定的“基本问题”的积累量以后，遇到一个新问题时，通过审题辨认，联想起与此类似的基本数学模型，从而提取出相应的方法来加以解决．‎ 例1：如图，已知直线，分别经过点和点，并且当两直线同时相交于轴正半轴的点时，恰好有．经过点、、的抛物线的对称轴与直线交于点．‎ ‎（1）求点的坐标，并求出抛物线的函数解析式；‎ ‎（2）抛物线的对称轴被直线，抛物线，直线和轴一次截得三条线段，问这三条线段有何数量关系？请说明理由．‎ ‎（3）当直线绕点旋转时，与抛物线的另一个交点为，请找出使为等腰三角形的点，简述理由，并写出点的坐标．‎ 首先，函数背景的问题由于已知条件“恰好有”促使我们想到几何中最常见的基本图形——“双垂直”图形：在中，，于，其中，，于是，，则点．进而，由待定系数法可直接求出直线，以及抛物线的解析式分别为，，．‎ 其次，考虑到点，，，分别是抛物线的对称轴分别与，抛物线，，轴的交点，根据上面求得的解析式可依次得出这四点的坐标：，，，，把所得坐标转化为线段长，所以三条线段．由函数解析式联立求交点坐标，由线段端点的坐标得出线段长，是同学们比较熟悉的解题步骤．‎ 最后，常规的等腰三角形的存在性问题，典型的分类讨论——三种情况，这都是我们平常学习中的基本功．已知两点，，确定第三点的位置，使得称为等腰三角形，分别以，为圆心，长为半径画弧，再作的垂直平分线，各自与抛物线的交点即为所求点．而利用抛物线的对称性不难求得点的坐标，．‎ 例2：在中，，点在线段上，，，垂足为，与相交于点．‎ ‎（1）当时，（如图1），‎ ‎①；②求的值；‎ ‎（2）当时（如图2），求的值（用含的式子表示）．‎ 已知条件中的“”这样的倍角、半角关系，通常在图形中转化为等角关系——要么作出的二倍角等于，要么作出的半角等于．而另一个条件“”显然要求作出的二倍角等于，这样就能形成最基本的等腰三角形的“三线合一”．至于与的比值，经验判断三角形相似，有了前面等腰三角形“三线合一”的基本图形，考虑到已知条件中的直角，自然又产生了相似三角形的基本图形，从而问题得解．‎ 我们先来分析一般情况：当时．如图3，延长至点，使得，连结，交于，易证是等腰三角形，那么，所以，由得．‎ 分析至此，这道题的高明与巧妙之处就显露出来了——原来点是三条高的交点，再连结并延长交于，则，联想到相似三角形的“斜”、“蝶形”等基本图形，∽，∽，所以，于是得到．‎ 由特殊与一般的关系，第（1）问中当时，即，所以此时的，而所求的则不难想到．‎ 今天的学习充分说明了化归到基本——基本图形、基本结论、基本方法等——是数学思考的最基本最重要的原则！‎