2020年江苏省扬州市中考数学试卷(含解析） 26页

‎2020年江苏省扬州市中考数学试卷 一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）‎ ‎1．（3分）（2020•扬州）实数3的相反数是（　　）‎ A．﹣3 B．‎1‎‎3‎ C．3 D．±3‎ ‎2．（3分）（2020•扬州）下列各式中，计算结果为m6的是（　　）‎ A．m2•m3 B．m3+m3 C．m12÷m2 D．（m2 ）3‎ ‎3．（3分）（2020•扬州）在平面直角坐标系中，点P（x2+2，﹣3）所在的象限是（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎4．（3分）（2020•扬州）“致中和，天地位焉，万物育焉．”对称美是我国古人和谐平衡思想的体现，常被运用于建筑、器物、绘画、标识等作品的设计上，使对称之美惊艳了千年的时光．在下列与扬州有关的标识或简图中，不是轴对称图形的是（　　）‎ A． ‎ B． ‎ C． ‎ D．‎ ‎5．（3分）（2020•扬州）某班级组织活动，为了解同学们喜爱的体育运动项目，设计了如图尚不完整的调查问卷：‎ 第26页（共26页）‎ 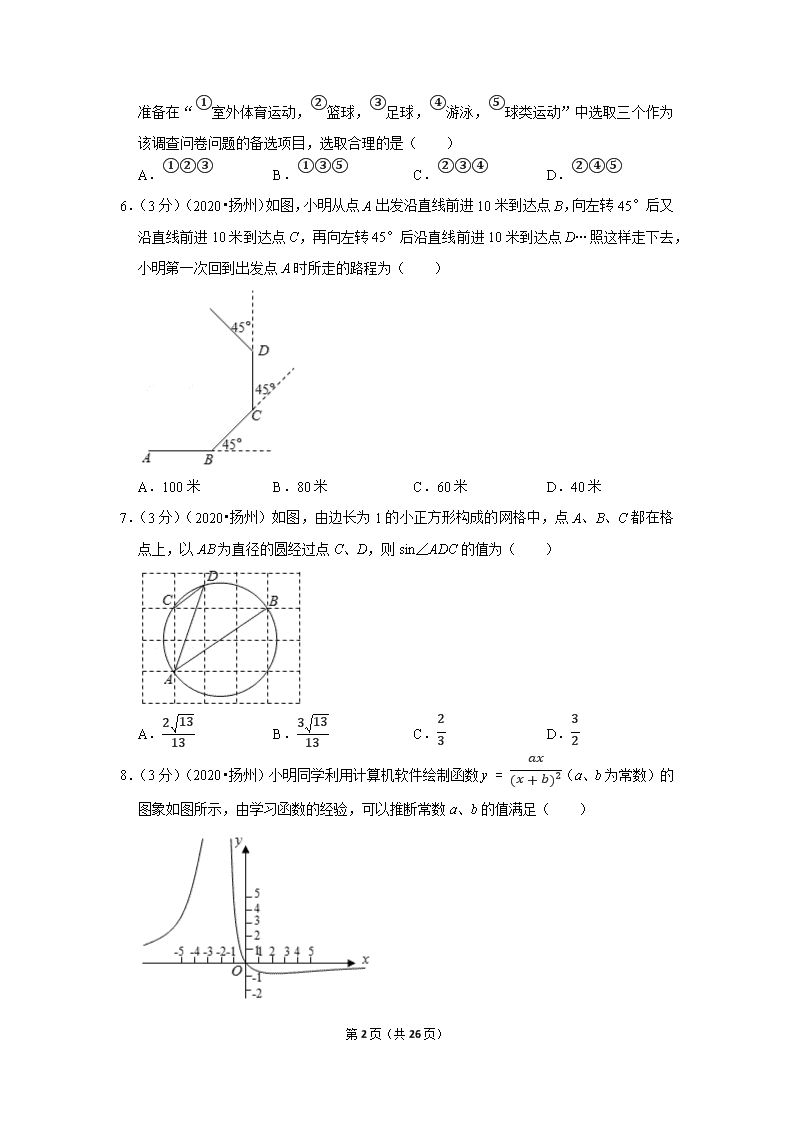准备在“①室外体育运动，②篮球，③足球，④游泳，⑤球类运动”中选取三个作为该调查问卷问题的备选项目，选取合理的是（　　）‎ A．①②③ B．①③⑤ C．②③④ D．②④⑤‎ ‎6．（3分）（2020•扬州）如图，小明从点A出发沿直线前进10米到达点B，向左转45°后又沿直线前进10米到达点C，再向左转45°后沿直线前进10米到达点D…照这样走下去，小明第一次回到出发点A时所走的路程为（　　）‎ A．100米 B．80米 C．60米 D．40米 ‎7．（3分）（2020•扬州）如图，由边长为1的小正方形构成的网格中，点A、B、C都在格点上，以AB为直径的圆经过点C、D，则sin∠ADC的值为（　　）‎ A．‎2‎‎13‎‎13‎ B．‎3‎‎13‎‎13‎ C．‎2‎‎3‎ D．‎‎3‎‎2‎ ‎8．（3分）（2020•扬州）小明同学利用计算机软件绘制函数y‎=‎ax‎(x+b‎)‎‎2‎（a、b为常数）的图象如图所示，由学习函数的经验，可以推断常数a、b的值满足（　　）‎ 第26页（共26页）‎ A．a＞0，b＞0 B．a＞0，b＜0 C．a＜0，b＞0 D．a＜0，b＜0‎ 二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）‎ ‎9．（3分）（2020•扬州）2020年6月23日，中国自主研发的北斗三号最后一颗卫星成功发射．据统计，国内已有超过6500000辆营运车辆导航设施应用北斗系统，数据6500000用科学记数法表示为　 　．‎ ‎10．（3分）（2020•扬州）分解因式：a3﹣2a2+a＝　 　．‎ ‎11．（3分）（2020•扬州）代数式x+2‎‎3‎在实数范围内有意义，则实数x的取值范围是　 　．‎ ‎12．（3分）（2020•扬州）方程（x+1）2＝9的根是　 　．‎ ‎13．（3分）（2020•扬州）圆锥的底面半径为3，侧面积为12π，则这个圆锥的母线长为　 　．‎ ‎14．（3分）（2020•扬州）《九章算术》是中国传统数学的重要著作之一，奠定了中国传统数学的基本框架．如图所示是其中记载的一道“折竹”问题：“今有竹高一丈，末折抵地，去根三尺，问折者高几何？”题意是：一根竹子原高1丈（1丈＝10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？答：折断处离地面　 　尺高．‎ ‎15．（3分）（2020•扬州）大数据分析技术为打赢疫情防控阻击战发挥了重要作用．如图是小明同学的健康码（绿码）示意图，用黑白打印机打印于边长为2cm的正方形区域内，为了估计图中黑色部分的总面积，在正方形区域内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在0.6左右，据此可以估计黑色部分的总面积约为　 　cm2．‎ 第26页（共26页）‎ ‎16．（3分）（2020•扬州）如图，工人师傅用扳手拧形状为正六边形的螺帽，现测得扳手的开口宽度b＝3cm，则螺帽边长a＝　 　cm．‎ ‎17．（3分）（2020•扬州）如图，在△ABC中，按以下步骤作图：‎ ‎①以点B为圆心，任意长为半径作弧，分别交AB、BC于点D、E．‎ ‎②分别以点D、E为圆心，大于‎1‎‎2‎DE的同样长为半径作弧，两弧交于点F．‎ ‎③作射线BF交AC于点G．‎ 如果AB＝8，BC＝12，△ABG的面积为18，则△CBG的面积为　 　．‎ ‎18．（3分）（2020•扬州）如图，在▱ABCD中，∠B＝60°，AB＝10，BC＝8，点E为边AB上的一个动点，连接ED并延长至点F，使得DF‎=‎‎1‎‎4‎DE，以EC、EF为邻边构造▱EFGC，连接EG，则EG的最小值为　 　．‎ 三、解答题（本大题共有10小题，共96分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）‎ ‎19．（8分）（2020•扬州）计算或化简：‎ ‎（1）2sin60°+（‎1‎‎2‎）﹣1‎-‎‎12‎．‎ ‎（2）x-1‎x‎÷‎x‎2‎‎-1‎x‎2‎‎+x．‎ 第26页（共26页）‎ ‎20．（8分）（2020•扬州）解不等式组x+5≤0，‎‎3x-1‎‎2‎‎≥2x+1，‎并写出它的最大负整数解．‎ ‎21．（8分）（2020•扬州）扬州教育推出的“智慧学堂”已成为同学们课外学习的得力助手．为了解同学们“智慧学堂”平台使用的熟练程度，某校随机抽取了部分同学进行调查，并将调查结果绘制成如图两幅尚不完整的统计图．‎ 根据以上信息，回答下列问题：‎ ‎（1）本次调查的样本容量是　 　，扇形统计图中表示A等级的扇形圆心角为　 　°；‎ ‎（2）补全条形统计图；‎ ‎（3）学校拟对“不太熟练或不熟练”的同学进行平台使用的培训，若该校有2000名学生，试估计该校需要培训的学生人数．‎ ‎22．（8分）（2020•扬州）防疫期间，全市所有学校都严格落实测体温进校园的防控要求．某校开设了A、B、C三个测温通道，某天早晨，该校小明和小丽两位同学将随机通过测温通道进入校园．‎ ‎（1）小明从A测温通道通过的概率是　 　；‎ ‎（2）利用画树状图或列表的方法，求小明和小丽从同一个测温通道通过的概率．‎ ‎23．（10分）（2020•扬州）如图，某公司会计欲查询乙商品的进价，发现进货单已被墨水污染．‎ 进货单 商品 进价（元/件）‎ 数量（件）‎ 总金额（元）‎ 甲 ‎7200‎ 乙 ‎3200‎ 商品采购员李阿姨和仓库保管员王师傅对采购情况回忆如下：‎ 李阿姨：我记得甲商品进价比乙商品进价每件高50%．‎ 第26页（共26页）‎ 王师傅：甲商品比乙商品的数量多40件．‎ 请你求出乙商品的进价，并帮助他们补全进货单．‎ ‎24．（10分）（2020•扬州）如图，▱ABCD的对角线AC、BD相交于点O，过点O作EF⊥AC，分别交AB、DC于点E、F，连接AF、CE．‎ ‎（1）若OE‎=‎‎3‎‎2‎，求EF的长；‎ ‎（2）判断四边形AECF的形状，并说明理由．‎ ‎25．（10分）（2020•扬州）如图，△ABC内接于⊙O，∠B＝60°，点E在直径CD的延长线上，且AE＝AC．‎ ‎（1）试判断AE与⊙O的位置关系，并说明理由；‎ ‎（2）若AC＝6，求阴影部分的面积．‎ ‎26．（10分）（2020•扬州）阅读感悟：‎ 有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：‎ 已知实数x、y满足3x﹣y＝5①，2x+3y＝7②，求x﹣4y和7x+5y的值．‎ 本题常规思路是将①②两式联立组成方程组，解得x、y的值再代入欲求值的代数式得到答案，常规思路运算量比较大．其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由①﹣②可得x﹣4y＝﹣2，由①+②×2可得7x+5y＝19．这样的解题思想就是通常所说的“整体思想”．‎ 解决问题：‎ 第26页（共26页）‎ ‎（1）已知二元一次方程组‎2x+y=7，‎x+2y=8，‎则x﹣y＝　 　，x+y＝　 　；‎ ‎（2）某班级组织活动购买小奖品，买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记本共需58元，则购买5支铅笔、5块橡皮、5本日记本共需多少元？‎ ‎（3）对于实数x、y，定义新运算：x*y＝ax+by+c，其中a、b、c是常数，等式右边是通常的加法和乘法运算．已知3*5＝15，4*7＝28，那么1*1＝　 　．‎ ‎27．（12分）（2020•扬州）如图1，已知点O在四边形ABCD的边AB上，且OA＝OB＝OC＝OD＝2，OC平分∠BOD，与BD交于点G，AC分别与BD、OD交于点E、F．‎ ‎（1）求证：OC∥AD；‎ ‎（2）如图2，若DE＝DF，求AEAF的值；‎ ‎（3）当四边形ABCD的周长取最大值时，求DEDF的值．‎ ‎28．（12分）（2020•扬州）如图，已知点A（1，2）、B（5，n）（n＞0），点P为线段AB上的一个动点，反比例函数y‎=‎kx（x＞0）的图象经过点P．小明说：“点P从点A运动至点B的过程中，k值逐渐增大，当点P在点A位置时k值最小，在点B位置时k值最大．”‎ ‎（1）当n＝1时．‎ ‎①求线段AB所在直线的函数表达式．‎ ‎②你完全同意小明的说法吗？若完全同意，请说明理由；若不完全同意，也请说明理由，并求出正确的k的最小值和最大值．‎ ‎（2）若小明的说法完全正确，求n的取值范围．‎ 第26页（共26页）‎ 第26页（共26页）‎ ‎2020年江苏省扬州市中考数学试卷 参考答案与试题解析 一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）‎ ‎1．（3分）（2020•扬州）实数3的相反数是（　　）‎ A．﹣3 B．‎1‎‎3‎ C．3 D．±3‎ ‎【解答】解：实数3的相反数是：﹣3．‎ 故选：A．‎ ‎2．（3分）（2020•扬州）下列各式中，计算结果为m6的是（　　）‎ A．m2•m3 B．m3+m3 C．m12÷m2 D．（m2 ）3‎ ‎【解答】解：A、m2•m3＝m5，故此选项不合题意；‎ B、m3+m3＝2m3，故此选项不合题意；‎ C、m12÷m2＝m10，故此选项不合题意；‎ D、（m2 ）3＝m6，故此选项符合题意．‎ 故选：D．‎ ‎3．（3分）（2020•扬州）在平面直角坐标系中，点P（x2+2，﹣3）所在的象限是（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【解答】解：∵x2+2＞0，‎ ‎∴点P（x2+2，﹣3）所在的象限是第四象限．‎ 故选：D．‎ ‎4．（3分）（2020•扬州）“致中和，天地位焉，万物育焉．”对称美是我国古人和谐平衡思想的体现，常被运用于建筑、器物、绘画、标识等作品的设计上，使对称之美惊艳了千年的时光．在下列与扬州有关的标识或简图中，不是轴对称图形的是（　　）‎ A． ‎ B． ‎ 第26页（共26页）‎ C． ‎ D．‎ ‎【解答】解：A、是轴对称图形，故本选项不合题意；‎ B、是轴对称图形，故本选项不合题意；‎ C、不是轴对称图形，故本选项符合题意；‎ D、是轴对称图形，故本选项不合题意．‎ 故选：C．‎ ‎5．（3分）（2020•扬州）某班级组织活动，为了解同学们喜爱的体育运动项目，设计了如图尚不完整的调查问卷：‎ 准备在“①室外体育运动，②篮球，③足球，④游泳，⑤球类运动”中选取三个作为该调查问卷问题的备选项目，选取合理的是（　　）‎ A．①②③ B．①③⑤ C．②③④ D．②④⑤‎ ‎【解答】解：根据体育项目的隶属包含关系，选择“篮球”“足球”“游泳”比较合理，‎ 故选：C．‎ ‎6．（3分）（2020•扬州）如图，小明从点A出发沿直线前进10米到达点B，向左转45°后又沿直线前进10米到达点C，再向左转45°后沿直线前进10米到达点D…照这样走下去，小明第一次回到出发点A时所走的路程为（　　）‎ 第26页（共26页）‎ A．100米 B．80米 C．60米 D．40米 ‎【解答】解：∵小明每次都是沿直线前进10米后向左转45度，‎ ‎∴他走过的图形是正多边形，‎ ‎∴边数n＝360°÷45°＝8，‎ ‎∴他第一次回到出发点A时，一共走了8×10＝80（m）．‎ 故选：B．‎ ‎7．（3分）（2020•扬州）如图，由边长为1的小正方形构成的网格中，点A、B、C都在格点上，以AB为直径的圆经过点C、D，则sin∠ADC的值为（　　）‎ A．‎2‎‎13‎‎13‎ B．‎3‎‎13‎‎13‎ C．‎2‎‎3‎ D．‎‎3‎‎2‎ ‎【解答】解：如图，连接BC．‎ ‎∵∠ADC和∠ABC所对的弧长都是AC，‎ ‎∴根据圆周角定理知，∠ADC＝∠ABC．‎ 在Rt△ACB中，根据锐角三角函数的定义知，‎ sin∠ABC‎=‎ACAB，‎ ‎∵AC＝2，BC＝3，‎ ‎∴AB‎=AC‎2‎+BC‎2‎=‎‎13‎，‎ ‎∴sin∠ABC‎=‎2‎‎13‎=‎‎2‎‎13‎‎13‎，‎ ‎∴sin∠ADC‎=‎‎2‎‎13‎‎13‎．‎ 故选：A．‎ 第26页（共26页）‎ ‎8．（3分）（2020•扬州）小明同学利用计算机软件绘制函数y‎=‎ax‎(x+b‎)‎‎2‎（a、b为常数）的图象如图所示，由学习函数的经验，可以推断常数a、b的值满足（　　）‎ A．a＞0，b＞0 B．a＞0，b＜0 C．a＜0，b＞0 D．a＜0，b＜0‎ ‎【解答】解：由图象可知，当x＞0时，y＜0，‎ ‎∴a＜0；‎ x＝﹣b时，函数值不存在，‎ ‎∴﹣b＜0，‎ ‎∴b＞0；‎ 故选：C．‎ 二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）‎ ‎9．（3分）（2020•扬州）2020年6月23日，中国自主研发的北斗三号最后一颗卫星成功发射．据统计，国内已有超过6500000辆营运车辆导航设施应用北斗系统，数据6500000用科学记数法表示为　6.5×106　．‎ ‎【解答】解：6500000用科学记数法表示应为：6.5×106，‎ 故答案为：6.5×106．‎ ‎10．（3分）（2020•扬州）分解因式：a3﹣2a2+a＝　a（a﹣1）2　．‎ ‎【解答】解：a3﹣2a2+a ‎＝a（a2﹣2a+1）‎ ‎＝a（a﹣1）2．‎ 故答案为：a（a﹣1）2．‎ ‎11．（3分）（2020•扬州）代数式x+2‎‎3‎在实数范围内有意义，则实数x的取值范围是　x≥﹣2　．‎ 第26页（共26页）‎ ‎【解答】解：代数式x+2‎‎3‎在实数范围内有意义，‎ 则x+2≥0，‎ 解得：x≥﹣2．‎ 故答案为：x≥﹣2．‎ ‎12．（3分）（2020•扬州）方程（x+1）2＝9的根是　x1＝2，x2＝﹣4　．‎ ‎【解答】解：（x+1）2＝9，‎ x+1＝±3，‎ x1＝2，x2＝﹣4．‎ 故答案为：x1＝2，x2＝﹣4．‎ ‎13．（3分）（2020•扬州）圆锥的底面半径为3，侧面积为12π，则这个圆锥的母线长为　4　．‎ ‎【解答】解：∵S侧＝πrl，‎ ‎∴3πl＝12π，‎ ‎∴l＝4．‎ 答：这个圆锥的母线长为4．‎ 故答案为：4．‎ ‎14．（3分）（2020•扬州）《九章算术》是中国传统数学的重要著作之一，奠定了中国传统数学的基本框架．如图所示是其中记载的一道“折竹”问题：“今有竹高一丈，末折抵地，去根三尺，问折者高几何？”题意是：一根竹子原高1丈（1丈＝10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？答：折断处离地面　4.55　尺高．‎ ‎【解答】解：设折断处离地面x尺，‎ 根据题意可得：x2+32＝（10﹣x）2，‎ 第26页（共26页）‎ 解得：x＝4.55．‎ 答：折断处离地面4.55尺．‎ 故答案为：4.55．‎ ‎15．（3分）（2020•扬州）大数据分析技术为打赢疫情防控阻击战发挥了重要作用．如图是小明同学的健康码（绿码）示意图，用黑白打印机打印于边长为2cm的正方形区域内，为了估计图中黑色部分的总面积，在正方形区域内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在0.6左右，据此可以估计黑色部分的总面积约为　2.4　cm2．‎ ‎【解答】解：∵经过大量重复试验，发现点落入黑色部分的频率稳定在0.6左右，‎ ‎∴点落入黑色部分的概率为0.6，‎ ‎∵边长为2cm的正方形的面积为4cm2，‎ 设黑色部分的面积为S，‎ 则S‎4‎‎=‎0.6，‎ 解得S＝2.4（cm2）．‎ 答：估计黑色部分的总面积约为2.4cm2．‎ 故答案为：2.4．‎ ‎16．（3分）（2020•扬州）如图，工人师傅用扳手拧形状为正六边形的螺帽，现测得扳手的开口宽度b＝3cm，则螺帽边长a＝　‎3‎　cm．‎ ‎【解答】解：如图，连接AC，过点B作BD⊥AC于D，‎ 由正六边形，得 ‎∠ABC＝120°，AB＝BC＝a，‎ ‎∠BCD＝∠BAC＝30°．‎ 由AC＝3，得CD＝1.5．‎ 第26页（共26页）‎ cos∠BCD‎=CDBC=‎‎3‎‎2‎，即‎1.5‎a‎=‎‎3‎‎2‎，‎ 解得a‎=‎‎3‎，‎ 故答案为：‎3‎．‎ ‎17．（3分）（2020•扬州）如图，在△ABC中，按以下步骤作图：‎ ‎①以点B为圆心，任意长为半径作弧，分别交AB、BC于点D、E．‎ ‎②分别以点D、E为圆心，大于‎1‎‎2‎DE的同样长为半径作弧，两弧交于点F．‎ ‎③作射线BF交AC于点G．‎ 如果AB＝8，BC＝12，△ABG的面积为18，则△CBG的面积为　27　．‎ ‎【解答】解：如图，过点G作GM⊥AB于点M，GN⊥AC于点N，‎ 根据作图过程可知：‎ BG是∠ABC的平分线，‎ ‎∴GM＝GN，‎ ‎∵△ABG的面积为18，‎ ‎∴‎1‎‎2‎‎×‎AB×GM＝18，‎ ‎∴4GM＝18，‎ 第26页（共26页）‎ ‎∴GM‎=‎‎9‎‎2‎，‎ ‎∴△CBG的面积为：‎1‎‎2‎‎×‎BC×GN‎=‎1‎‎2‎×‎12‎×‎9‎‎2‎=‎27．‎ 故答案为：27．‎ ‎18．（3分）（2020•扬州）如图，在▱ABCD中，∠B＝60°，AB＝10，BC＝8，点E为边AB上的一个动点，连接ED并延长至点F，使得DF‎=‎‎1‎‎4‎DE，以EC、EF为邻边构造▱EFGC，连接EG，则EG的最小值为　9‎3‎　．‎ ‎【解答】解：作CH⊥AB于点H，‎ ‎∵在▱ABCD中，∠B＝60°，BC＝8，‎ ‎∴CH＝4‎3‎，‎ ‎∵四边形ECGF是平行四边形，‎ ‎∴EF∥CG，‎ ‎∴△EOD∽△GOC，‎ ‎∴EOGO‎=DOOC=‎EDGC，‎ ‎∵DF‎=‎‎1‎‎4‎DE，‎ ‎∴DEEF‎=‎‎4‎‎5‎，‎ ‎∴EDGC‎=‎‎4‎‎5‎，‎ ‎∴EOGO‎=‎‎4‎‎5‎，‎ ‎∴当EO取得最小值时，EG即可取得最小值，‎ 当EO⊥CD时，EO取得最小值，‎ ‎∴CH＝EO，‎ ‎∴EO＝4‎3‎，‎ ‎∴GO＝5‎3‎，‎ 第26页（共26页）‎ ‎∴EG的最小值是‎9‎‎3‎，‎ 故答案为：9‎3‎．‎ 三、解答题（本大题共有10小题，共96分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）‎ ‎19．（8分）（2020•扬州）计算或化简：‎ ‎（1）2sin60°+（‎1‎‎2‎）﹣1‎-‎‎12‎．‎ ‎（2）x-1‎x‎÷‎x‎2‎‎-1‎x‎2‎‎+x．‎ ‎【解答】解：（1）原式＝2‎×‎3‎‎2‎+‎2﹣2‎‎3‎ ‎=‎3‎+‎‎2﹣2‎3‎ ‎ ‎＝2‎-‎‎3‎；‎ ‎（2）原式‎=‎x-1‎x•‎x(x+1)‎‎(x-1)(x+1)‎ ‎＝1．‎ ‎20．（8分）（2020•扬州）解不等式组x+5≤0，‎‎3x-1‎‎2‎‎≥2x+1，‎并写出它的最大负整数解．‎ ‎【解答】解：解不等式x+5≤0，得x≤﹣5，‎ 解不等式‎3x-1‎‎2‎‎≥‎2x+1，得：x≤﹣3，‎ 则不等式组的解集为x≤﹣5，‎ 所以不等式组的最大负整数解为﹣5．‎ ‎21．（8分）（2020•扬州）扬州教育推出的“智慧学堂”已成为同学们课外学习的得力助手．为了解同学们“智慧学堂”平台使用的熟练程度，某校随机抽取了部分同学进行调查，并将调查结果绘制成如图两幅尚不完整的统计图．‎ 第26页（共26页）‎ 根据以上信息，回答下列问题：‎ ‎（1）本次调查的样本容量是　500　，扇形统计图中表示A等级的扇形圆心角为　108　°；‎ ‎（2）补全条形统计图；‎ ‎（3）学校拟对“不太熟练或不熟练”的同学进行平台使用的培训，若该校有2000名学生，试估计该校需要培训的学生人数．‎ ‎【解答】解：（1）本次调查的样本容量是150÷30%＝500，‎ 扇形统计图中表示A等级的扇形圆心角为：360°×30%＝108°，‎ 故答案为：500，108；‎ ‎（2）B等级的人数为：500×40%＝200，‎ 补全的条形统计图如右图所示；‎ ‎（3）2000‎×‎50‎‎500‎=‎200（人），‎ 答：该校需要培训的学生人有200人．‎ ‎22．（8分）（2020•扬州）防疫期间，全市所有学校都严格落实测体温进校园的防控要求．某校开设了A、B、C三个测温通道，某天早晨，该校小明和小丽两位同学将随机通过测温通道进入校园．‎ ‎（1）小明从A测温通道通过的概率是　‎1‎‎3‎　；‎ ‎（2）利用画树状图或列表的方法，求小明和小丽从同一个测温通道通过的概率．‎ 第26页（共26页）‎ ‎【解答】解：（1）小明从A测温通道通过的概率是‎1‎‎3‎，‎ 故答案为：‎1‎‎3‎；‎ ‎（2）列表格如下：‎ A B C A A，A B，A C，A B A，B B，B C，B C A，C B，C C，C 由表可知，共有9种等可能的结果，其中小明和小丽从同一个测温通道通过的有3种可能，‎ 所以小明和小丽从同一个测温通道通过的概率为‎3‎‎9‎‎=‎‎1‎‎3‎．‎ ‎23．（10分）（2020•扬州）如图，某公司会计欲查询乙商品的进价，发现进货单已被墨水污染．‎ 进货单 商品 进价（元/件）‎ 数量（件）‎ 总金额（元）‎ 甲 ‎7200‎ 乙 ‎3200‎ 商品采购员李阿姨和仓库保管员王师傅对采购情况回忆如下：‎ 李阿姨：我记得甲商品进价比乙商品进价每件高50%．‎ 王师傅：甲商品比乙商品的数量多40件．‎ 请你求出乙商品的进价，并帮助他们补全进货单．‎ ‎【解答】解：设乙商品的进价为x元/件，则甲商品的进价为（1+50%）x元/件，‎ 依题意，得：‎7200‎‎(1+50%)x‎-‎3200‎x=‎40，‎ 解得：x＝40，‎ 经检验，x＝40是原方程的解，且符合题意，‎ ‎∴（1+50%）x＝60，‎3200‎x‎=‎80，‎7200‎‎(1+50%)x‎=‎120．‎ 答：甲商品的进价为60元/件，乙商品的进价为40元/件，购进甲商品120件，购进乙商品80件．‎ 第26页（共26页）‎ ‎24．（10分）（2020•扬州）如图，▱ABCD的对角线AC、BD相交于点O，过点O作EF⊥AC，分别交AB、DC于点E、F，连接AF、CE．‎ ‎（1）若OE‎=‎‎3‎‎2‎，求EF的长；‎ ‎（2）判断四边形AECF的形状，并说明理由．‎ ‎【解答】解：（1）∵四边形ABCD是平行四边形，‎ ‎∴AB∥CD，AO＝CO，‎ ‎∴∠FCO＝∠EAO，‎ 又∵∠AOE＝∠COF，‎ ‎∴△AOE≌△COF（ASA），‎ ‎∴OE＝OF‎=‎‎3‎‎2‎，‎ ‎∴EF＝2OE＝3；‎ ‎（2）四边形AECF是菱形，‎ 理由：∵△AOE≌△COF，‎ ‎∴AE＝CF，‎ 又∵AE∥CF，‎ ‎∴四边形AECF是平行四边形，‎ 又∵EF⊥AC，‎ ‎∴四边形AECF是菱形．‎ ‎25．（10分）（2020•扬州）如图，△ABC内接于⊙O，∠B＝60°，点E在直径CD的延长线上，且AE＝AC．‎ 第26页（共26页）‎ ‎（1）试判断AE与⊙O的位置关系，并说明理由；‎ ‎（2）若AC＝6，求阴影部分的面积．‎ ‎【解答】（1）证明：连接OA、AD，如图，‎ ‎∵CD为⊙O的直径，‎ ‎∴∠DAC＝90°，‎ 又∵∠ADC＝∠B＝60°，‎ ‎∴∠ACD＝30°，‎ 又∵AE＝AC，OA＝OD，‎ ‎∴△ADO为等边三角形，‎ ‎∴∠E＝30°，∠ADO＝∠DAO＝60°，‎ ‎∴∠PAD＝30°，‎ ‎∴∠EAD+∠DAO＝90°，‎ ‎∴OA⊥E，‎ ‎∴AE为⊙O的切线；‎ ‎（2）解：作OF⊥AC于F，‎ 由（1）可知△AEO为直角三角形，且∠E＝30°，‎ ‎∴OA＝2‎3‎，AE＝6，‎ ‎∴阴影部分的面积为‎1‎‎2‎‎×‎6×2‎3‎‎-‎60π×(2‎‎3‎‎)‎‎2‎‎360‎=‎6‎3‎‎-‎2π．‎ 故阴影部分的面积为6‎3‎‎-‎2π．‎ 第26页（共26页）‎ ‎26．（10分）（2020•扬州）阅读感悟：‎ 有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：‎ 已知实数x、y满足3x﹣y＝5①，2x+3y＝7②，求x﹣4y和7x+5y的值．‎ 本题常规思路是将①②两式联立组成方程组，解得x、y的值再代入欲求值的代数式得到答案，常规思路运算量比较大．其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由①﹣②可得x﹣4y＝﹣2，由①+②×2可得7x+5y＝19．这样的解题思想就是通常所说的“整体思想”．‎ 解决问题：‎ ‎（1）已知二元一次方程组‎2x+y=7，‎x+2y=8，‎则x﹣y＝　﹣1　，x+y＝　5　；‎ ‎（2）某班级组织活动购买小奖品，买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记本共需58元，则购买5支铅笔、5块橡皮、5本日记本共需多少元？‎ ‎（3）对于实数x、y，定义新运算：x*y＝ax+by+c，其中a、b、c是常数，等式右边是通常的加法和乘法运算．已知3*5＝15，4*7＝28，那么1*1＝　﹣11　．‎ ‎【解答】解：（1）‎2x+y=7①‎x+2y=8②‎．‎ 由①﹣②可得：x﹣y＝﹣1，‎ 由‎1‎‎3‎（①+②）可得：x+y＝5．‎ 故答案为：﹣1；5．‎ ‎（2）设铅笔的单价为m元，橡皮的单价为n元，日记本的单价为p元，‎ 依题意，得：‎20m+3n+2p=32①‎‎39m+5n+3p=58②‎，‎ 由2×①﹣②可得m+n+p＝6，‎ ‎∴5m+5n+5p＝5×6＝30．‎ 答：购买5支铅笔、5块橡皮、5本日记本共需30元．‎ ‎（3）依题意，得：‎3a+5b+c=15①‎‎4a+7b+c=28②‎，‎ 由3×①﹣2×②可得：a+b+c＝﹣11，‎ 即1*1＝﹣11．‎ 故答案为：﹣11．‎ 第26页（共26页）‎ ‎27．（12分）（2020•扬州）如图1，已知点O在四边形ABCD的边AB上，且OA＝OB＝OC＝OD＝2，OC平分∠BOD，与BD交于点G，AC分别与BD、OD交于点E、F．‎ ‎（1）求证：OC∥AD；‎ ‎（2）如图2，若DE＝DF，求AEAF的值；‎ ‎（3）当四边形ABCD的周长取最大值时，求DEDF的值．‎ ‎【解答】（1）证明：∵AO＝OD，‎ ‎∴∠OAD＝∠ADO，‎ ‎∵OC平分∠BOD，‎ ‎∴∠DOC＝∠COB，‎ 又∵∠DOC+∠COB∠＝∠OAD+∠ADO，‎ ‎∴∠ADO＝∠DOC，‎ ‎∴CO∥AD；‎ ‎（2）解：如图1，‎ ‎∵OA＝OB＝OC，‎ ‎∴∠ADB＝90°，‎ ‎∴△AOD和△ABD为等腰直角三角形，‎ ‎∴AD‎=‎‎2‎AO，‎ 第26页（共26页）‎ ‎∴ADAO‎=‎‎2‎，‎ ‎∵DE＝EF，‎ ‎∴∠DFE＝∠DEF，‎ ‎∵∠DFE＝∠AFO，‎ ‎∴∠AFO＝∠AED，‎ 又∠ADE＝∠AOF＝90°，‎ ‎∴△ADE∽△AOF，‎ ‎∴AEAF‎=ADAO=‎‎2‎．‎ ‎（3）解：如图2，‎ ‎∵OD＝OB，∠BOC＝∠DOC，‎ ‎∴△BOC≌△DOC（SAS），‎ ‎∴BC＝CD，‎ 设BC＝CD＝x，CG＝m，则OG＝2﹣m，‎ ‎∵OB2﹣OG2＝BC2﹣CG2，‎ ‎∴4﹣（2﹣m）2＝x2﹣m2，‎ 解得：m‎=‎‎1‎‎4‎x‎2‎，‎ ‎∴OG＝2‎-‎‎1‎‎4‎x‎2‎，‎ ‎∵OD＝OB，∠DOG＝∠BOG，‎ ‎∴G为BD的中点，‎ 又∵O为AB的中点，‎ ‎∴AD＝2OG＝4‎-‎‎1‎‎2‎x‎2‎，‎ ‎∴四边形ABCD的周长为2BC+AD+AB＝2x+4‎-‎1‎‎2‎x‎2‎+‎4‎=-‎1‎‎2‎x‎2‎+‎2x+8‎=-‎1‎‎2‎(x-2‎)‎‎2‎+‎10，‎ 第26页（共26页）‎ ‎∵‎-‎1‎‎2‎＜‎0，‎ ‎∴x＝2时，四边形ABCD的周长有最大值为10．‎ ‎∴BC＝2，‎ ‎∴△BCO为等边三角形，‎ ‎∴∠BOC＝60°，‎ ‎∵OC∥AD，‎ ‎∴∠DAC＝∠COB＝60°，‎ ‎∴∠ADF＝∠DOC＝60°，∠DAE＝30°，‎ ‎∴∠AFD＝90°，‎ ‎∴DEDA‎=‎‎3‎‎3‎，DF‎=‎‎1‎‎2‎DA，‎ ‎∴DEDF‎=‎‎2‎‎3‎‎3‎．‎ ‎28．（12分）（2020•扬州）如图，已知点A（1，2）、B（5，n）（n＞0），点P为线段AB上的一个动点，反比例函数y‎=‎kx（x＞0）的图象经过点P．小明说：“点P从点A运动至点B的过程中，k值逐渐增大，当点P在点A位置时k值最小，在点B位置时k值最大．”‎ ‎（1）当n＝1时．‎ ‎①求线段AB所在直线的函数表达式．‎ ‎②你完全同意小明的说法吗？若完全同意，请说明理由；若不完全同意，也请说明理由，并求出正确的k的最小值和最大值．‎ ‎（2）若小明的说法完全正确，求n的取值范围．‎ ‎【解答】解：（1）①当n＝1时，B（5，1），‎ 设线段AB所在直线的函数表达式为y＝kx+b，‎ 把A（1，2）和B（5，1）代入得：k+b=2‎‎5k+b=1‎，‎ 第26页（共26页）‎ 解得：k=-‎‎1‎‎4‎b=‎‎9‎‎4‎，‎ 则线段AB所在直线的函数表达式为y‎=-‎‎1‎‎4‎x‎+‎‎9‎‎4‎；‎ ‎②不完全同意小明的说法，理由为：‎ k＝xy＝x（‎-‎‎1‎‎4‎x‎+‎‎9‎‎4‎）‎=-‎‎1‎‎4‎（x‎-‎‎9‎‎2‎）2‎+‎‎81‎‎16‎，‎ ‎∵1≤x≤5，‎ ‎∴当x＝1时，kmin＝2；‎ 当x‎=‎‎9‎‎2‎时，kmax‎=‎‎81‎‎16‎，‎ 则不完全同意；‎ ‎（2）当n＝2时，A（1，2），B（5，2），符合；‎ 当n≠2时，y‎=‎n-2‎‎4‎x‎+‎‎10-n‎4‎，‎ k＝x（n-2‎‎4‎x‎+‎‎10-n‎4‎）‎=‎n-2‎‎4‎（x‎-‎n-10‎‎2n-4‎）2‎+‎‎(10-n‎)‎‎2‎‎16(2-n)‎，‎ 先增大当x取‎9‎‎2‎时，k为‎81‎‎16‎，为最大，到B为5时减小，‎ 即在直线上A到x‎=‎‎9‎‎2‎时增大，到5时减小，‎ 当‎9‎‎2‎‎＜‎x≤5时，k在减小，‎ 当n＜2时，k随x的增大而增大，则有n-10‎‎2n-4‎‎≥‎5，‎ 此时‎10‎‎9‎‎≤‎n＜2；‎ 当n＞2时，k随x的增大而增大，则有n-10‎‎2n-4‎‎≤‎1，‎ 此时n＞2，‎ 综上，n‎≥‎‎10‎‎9‎．‎ 第26页（共26页）‎