中考数学模拟试题及答案4 13页

‎2012年最新中考数学模拟试题四 ‎*考试时间120分钟　试卷满分150分 一、选择题（下列各题的备选答案中，只有一个答案是正确的，将正确答案的序号填在题后的括号内，每小题3分，共24分）‎ ‎1．sin30°的值为（ ）‎ A．　　　　　B．　　　　　　C．　　　　　　　D．‎ ‎2． △ABC中，∠A＝50°，∠B＝60°，则∠C＝（ ）‎ A．50° B．60° C．70° D．80°‎ ‎3．如图，直线l、l、l表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（　　）‎ A．一处．　　 B．两处　　　　C．三处．　　　　 D．四处．‎ ‎4．点P（－2，1）关于x轴对称的点的坐标是（　　）‎ A．（－2，－1）　　　B．（2，－1）　　C．（1，－2）　　　D．（2，1）‎ ‎5． 若x＝3是方程x－3mx＋6m＝0的一个根，则m的值为 （　　）‎ ‎　　　A．1 　　　　　　B． 2 　　　　　 C．3 　　　　　 D．4‎ ‎6．现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）.用小莉掷A立方体朝上的数字为、小明 掷B立方体朝上的数字为来确定点P（），那么它们各掷一次所确定的点P落在已知抛物线上的概率为（ ）‎ ‎ A. B. C. D.‎ ‎7．右图是由几个小立方块搭成的几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，那么这个几何体的主视图是（ ）‎ ‎2‎ ‎1‎ ‎3‎ A． B． C． D．‎ ‎8．某超级市场失 窃，大量的商品在夜间被罪犯用汽车运走。三个嫌疑犯被警察局传讯，警察局已经掌握了以下事实：（１）罪犯不在A、B、C三人之外；（２）C作案时总得有A作从犯；（３）B不会开车。在此案中能肯定的作案对象是（ ）‎ ‎ A．嫌疑犯A 　　B．嫌疑犯B C．嫌疑犯C D．嫌疑犯A和C 二、填空题（每小题3分，共24分）‎ ‎9．据中新社报道：2010年我国粮食产量将达到540000000000千克，用科学记数法表示这个粮食产量为______千克.‎ ‎10．用一个半径为6㎝的半圆围成一个圆锥的侧面，则这个圆锥的侧面积为 ㎝2.（结果保留）‎ ‎11．△ABC中，AB＝6，AC＝4，∠A＝45°，则△ABC的面积为　　　　．‎ ‎12．若一次函数的图象经过反比例函数图象上的两点（1，m）和（n，2），则这个一次函数的解析式是 .‎ ‎13． 某品牌的牛奶由于质量问题，在市场上受到严重冲击，该乳业公司为了挽回市场，加大了产品质量的管理力度，并采取了“买二赠一”的促销手段，一袋鲜奶售价1.4元，一箱牛奶18袋，如果要买一箱牛奶，应该付款 元.‎ ‎14．通过平移把点A(2，－3)移到点A’(4，－2)，按同样的平移方式，点B(3，1)移到点B′, 则点B′的坐标是 ________‎ ‎15．如图，在甲、乙两地之间修一条笔直的公路，‎ 从甲地测得公路的走向是北偏东48°。甲、乙两地间 乙 北 甲 北 同时开工，若干天后，公路准确接通，则乙地所修公 路的走向是南偏西 度。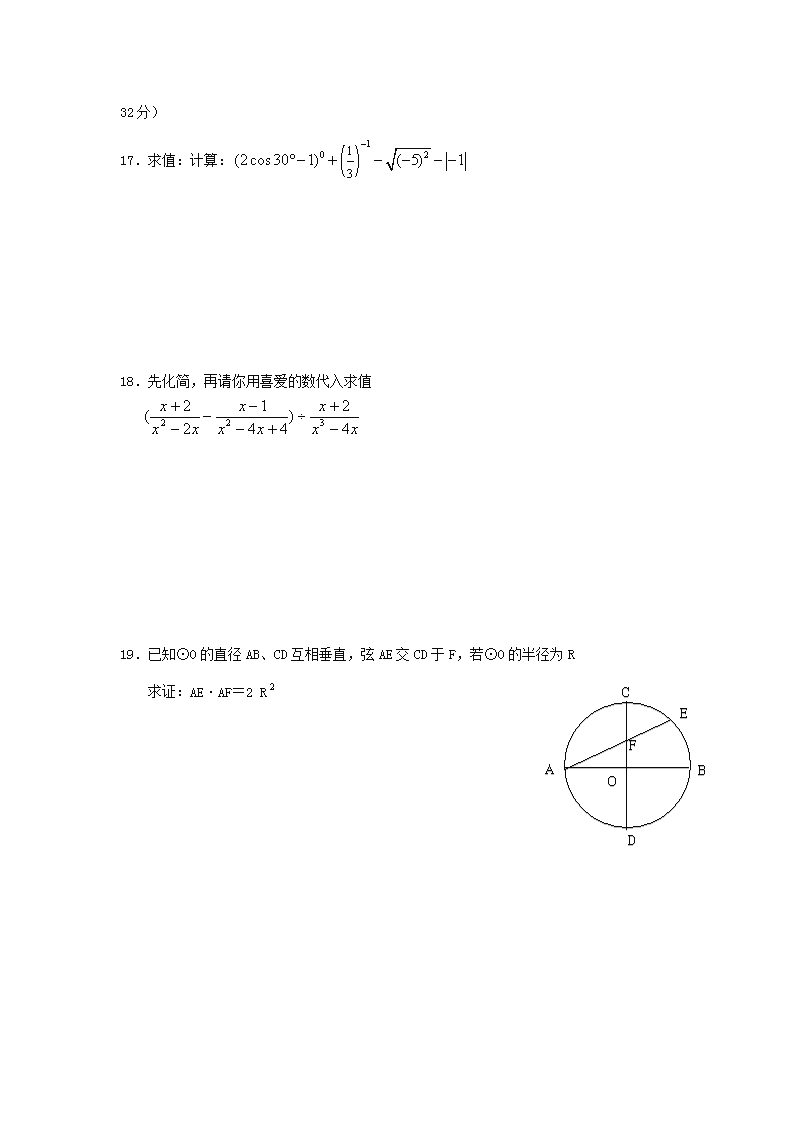‎ ‎16．如图，M为双曲线y＝上的一点，过点Ｍ作ｘ轴、ｙ轴的垂线，分别交直线ｙ＝－ｘ＋m于D、C两点，若直线ｙ＝－ｘ＋m与ｙ轴交于点Ａ，与ｘ轴相交于点B．则AD·BC的值为　　　　　　．‎ 三、（第17小题6分，第18、19小题各8分，第20小题10分，共32分）‎ ‎17．求值：计算：‎ ‎18．先化简，再请你用喜爱的数代入求值 ‎19．已知⊙O的直径AB、CD互相垂直，弦AE交CD于F，若⊙O的半径为R 求证：AE·AF＝2 R ‎20．据统计某外贸公司2007年、2008年的进出口贸易总额分别为3300万元和3760万元, 其中2008年的进口和出口贸易额分别比2007年增长20%和10%. ‎ (1) 试确定2007年该公司的进口和出口贸易额分别是多少万元;‎ (2) ‎2009年该公司的目标是：进出口贸易总额不低于4200万元, 其中出口贸易额所占比重不低于60%, 预计2009年的进口贸易额比2008年增长10%, 则为完成上述目标，2009年的出口贸易额比2008年至少应增加多少万元?‎ 四、（每小题10分，共20分）‎ ‎21．如图，河中水中停泊着一艘小艇，王平在河岸边的A处测得∠DAC＝α，李月在河岸边的的B处测得∠DCA＝β，如果A、C之间的距离为ｍ，求小艇D到河岸AC的距离． ‎ ‎22．某书报亭开设两种租书方式：一种是零星租书，每册收费1元；另一种是会员卡租书，办卡费每月12元，租书费每册0.4元．小军经常来该店租书，若每月租书数量为x册.‎ ‎（1）写出零星租书方式应付金额y1(元)与租书数量x（册）之间的函数关系式；‎ ‎（2）写出会员卡租书方式应付金额y2(元 )与租书数量x(册)之间的函数关系式；‎ ‎（3）小军选取哪种租书方式更合算？‎ 五、（本题12分）‎ ‎23． 如图所示，矩形ABCD中，点E在CB的延长线上，使CE＝AC，连结AE，点F是AE的中点，连结BF、DF，求证：BF⊥DF 六、（本题12分）‎ ‎24．某校为了了解九年级学生的体能情况，抽调了一部分学生进行一分钟跳绳测试，将测试成绩整理后作出如下统计图．甲同学计算出前两组的频率和是0.12，乙同学计算出跳绳次数不少于100次的同学占96％，丙同学计算出从左至右第二、三、四组的频数比为4：17：15．结合统计图回答下列问题：‎ ‎ (1)这次共抽调了多少人?‎ ‎ (2)若跳绳次数不少于130次为优秀，则这次测试成绩的优秀率是多少?‎ ‎ (3)如果这次测试成绩的中位数是120次，那么这次测试中，成绩为120次的学生至少有多少人?‎ 七、（本题12分）‎ ‎25．在△ABC中，AC＝BC，∠ACB＝90°，D、E是直线AB上两点．∠DCE＝45°‎ ‎（１）当CE⊥AB时，点D与点A重合，显然DE＝AD＋BE（不必证明）‎ ‎（２）如图，当点D不与点A重合时，求证：DE＝AD＋BE ‎（３）当点D在BA的延长线上时，（２）中的结论是否成立？画出图形，说明理由． ‎ 八（本题14分）‎ ‎26．如图，已知抛物线ｙ＝ｘ－ａｘ＋ａ－4ａ－4与ｘ轴相交于点A和点B，与ｙ轴相交于点D（0，8），直线DC平行于ｘ轴，交抛物线于另一点C，动点P以每秒2个单位长度的速度从C点出发，沿C→D运动，同时，点Q以每秒1个单位长度的速度从点A出发，沿A→B运动，连接PQ、CB，设点P运动的时间为t秒．‎ ‎（１）求ａ的值；‎ ‎（２）当四边形ODPQ为矩形时，求这个矩形的面积；‎ ‎（３）当四边形PQBC的面积等于14时，求t的值．‎ ‎（４）当t为何值时，△PBQ是等腰三角形？（直接写出答案）‎ ‎ ‎ 数学试题参考答案及评分标准 一、选择题（每小题3分，共24分）‎ ‎1．Ａ；2．C； 3．D；4．A；5．C； 6．； 7．A； 8．A 二、填空题（每小题3分，共24分）‎ ‎9．5.4×10；10．18π； 11．6；　　12．ｙ＝－2ｘ－2；　13．16.8； ‎ ‎14．（5，2） ；15．48°；　　16．2‎ 三、（第17小题6分，第18、19小题各8分，第20小题10分，共32分）‎ ‎17．解：原式 3分 ‎． 4分 当时，‎ 原式 ‎ 6分 ‎18. 解：原式＝………………3分 ‎＝ｘ＋2－………………5分 ‎＝………………6分 当ｘ＝6时，原式＝………………8分 ‎ ‎ ‎19．证明：连接BE…………………1分 ‎∵AB为⊙O的直径 ‎∴∠AEB＝90°…………………2分 ‎∵AB⊥CD ‎∴∠AOF＝90°‎ ‎∴∠AOF＝∠AEB＝90°‎ 又∠A＝∠A ‎∴△AOF∽△AEB…………………5分 ‎∴AE·AF＝AO·AB ‎∵AO＝R　AB＝2R AE·AF＝2R………………8分 ‎ 20．解：设2007年进口贸易额为x万元、出口贸易额为y万元 则： ‎ ‎∴ 2007年进口贸易额为1300万元、出口贸易额为2000万元 ‎（2）设2009年的出口贸易额比2008年至少增加z万元 由2008年的进口贸易额是：1300（1+20%）=1560万元 ‎ ‎2008年的出口贸易额是：2000（1+10%）=2200万元 ‎ 则： ‎ ‎ 解得 ‎ 所以z≥374 ，即2009年的出口贸易额比2008年至少增加374万元．……………10分 四．（每小题10分，共20分）‎ ‎21．解：过点D作DB⊥AC于点Ｂ，设DB＝ｘ………1分 在Rt△ADB中，tan∠DAB＝‎ ‎∴AB＝………4分 在Rt△CDB中，tan∠DCB＝‎ ‎∴BC＝‎ ‎∵AB＋BC＝AC＝ｍ ‎∴＋＝ｍ………8分 解得：ｘ＝‎ 答：小艇D到河岸AB的距离为………10分 ‎22．解：（１）ｙ＝ｘ．．．．．．．．．．2分 ‎（２）ｙ＝12＋0.4ｘ．．．．．．．．．．4分 ‎（３）当ｙ＝ｙ时，ｘ＝12＋0.4ｘ，解得：ｘ＝20‎ 当ｙ＞ｙ时，ｘ＞12＋0.4ｘ，解得ｘ＞20‎ 当ｙ＜ｙ时，ｘ＜12＋0.4ｘ，解得ｘ＜20‎ 综上所述，当小军每月借书少于20册时，采用零星方式租书合算；当每月租书20册时，两种方式费用一样；当每月租书多于20册时，采用会员的方式更合算．．．．．．．．．．．10分 ‎ ‎ ‎23．证明：延长BF，交DA的延长线于点M，连接BD……………2分 ‎∵四边形ABCD是矩形 ‎∴MD∥BC ‎∴∠AMF＝∠EBF　∠E＝∠MAF 又FA＝FE ‎∴△AFM≌△EFB……………5分 AM＝BE　FB＝FM 矩形ABCD中，AC＝BD，AD＝BC ‎∴BC＋BE＝AD＋AM 即CE＝MD ‎∵CE＝AC ‎∴DB＝DM ‎∵FB＝FM ‎∴BF⊥DF……………12分 ‎24．(1)第一组的频率为1-0.96=0.04…………………………………………2分 ‎ 第二组的频率为0.12-0.04=O.08…………………………………………3分 ‎ =150(人)，这次共抽调了150人……………………………………6分 ‎ (2)第一组人数为150×0.04=6(人)，第三、四组人数分别为51人，45人………8分 ‎ 这次测试的优秀率为×100％=24％………………………………10分 ‎ (3)成绩为120次的学生至少有7人…………………………………………12分 七、‎ ‎25．解：（２）证明：‎ 过点A作AF ⊥AB ，使AF＝AB，连接DF ‎∵△ABC是等腰直角三角形 ‎∴AC＝AB　∠CAB＝∠B＝45°，‎ ‎∴∠FAC＝45°‎ ‎∴△CAF≌△CBE…………………………………………3分 ‎∴CF＝CE　∠ACF＝∠BCE ‎∵∠ACB＝90°，∠DCE＝45°‎ ‎∴∠ACD＋∠BCE＝45°‎ ‎∴∠ACD＋∠ACF＝45°‎ 即∠DCF＝45°‎ ‎∴∠DCF＝∠DCE 又CD＝CD ‎∴△CDF≌△CDE ‎∴DF＝DE ‎∵AD＋AF＝DF ‎∴AD＋BE＝DE…………………………………………7分 ‎（３）结论仍然成立 如图 证法同（２）…………………………………………12分 八、（本题14分）‎ ‎26．（１）∵抛物线ｙ＝ｘ－ａｘ＋ａ－4ａ－4经过点（0，8）‎ ‎∴ａ－4ａ－4＝8‎ 解得：ａ＝6，ａ＝－2（不合题意，舍去）‎ ‎∴ａ的值为6…………………………………………4分 ‎（２）由（１）可得抛物线的解析式为 ｙ＝ｘ－6ｘ＋8‎ 当ｙ＝0时，ｘ－6ｘ＋8＝0‎ 解得：ｘ＝2，ｘ＝4‎ ‎∴A点坐标为（2，0），B点坐标为（4，0）‎ 当ｙ＝8时，‎ ｘ＝0或ｘ＝6‎ ‎∴D点的坐标为（0，8），C点坐标为（6，8）‎ DP＝6－2t，OQ＝2＋ｔ 当四边形OQPD为矩形时，DP＝OQ ‎2＋t＝6－2t，t＝，OQ＝2＋＝‎ S＝8×＝‎ 即矩形OQPD的面积为…………………………………………8分 ‎（３）四边形PQBC的面积为，当此四边形的面积为14时，‎ ‎（2－t＋2t）×8＝14‎ 解得t＝（秒）‎ 当t＝时，四边形PQBC的面积为14…………………………………………12分 ‎（４）t＝时，PBQ是等腰三角形．…………………………………………14分 ‎