上海中考数学几何练习题四大名校冲刺练习 13页

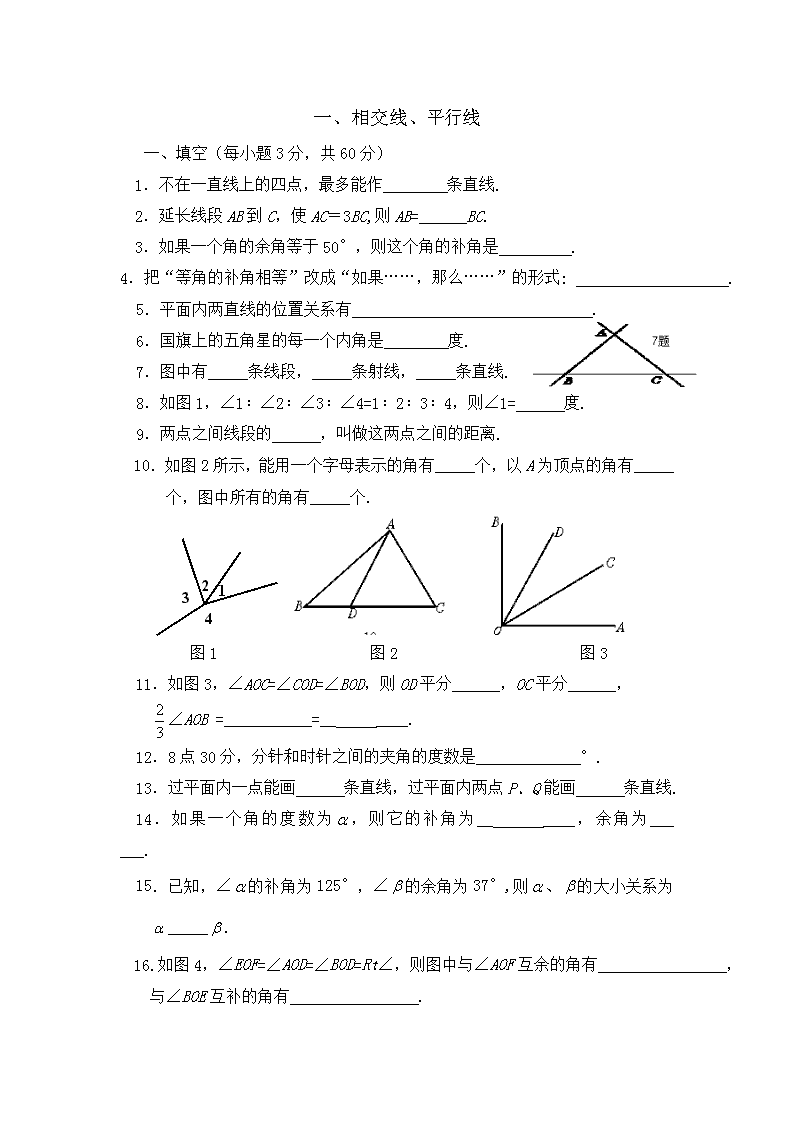
一、相交线、平行线 一、 填空（每小题3分，共60分）‎ 1． 不在一直线上的四点，最多能作 条直线.‎ 2． 延长线段AB到C，使AC＝3BC,则AB=______BC.‎ 3． 如果一个角的余角等于50°，则这个角的补角是 .‎ ‎4．把“等角的补角相等”改成“如果……，那么……”的形式: .‎ ‎ 5．平面内两直线的位置关系有 .‎ ‎ 6．国旗上的五角星的每一个内角是 度.‎ ‎7．图中有_____条线段，_____条射线，_____条直线.‎ ‎8．如图1，∠1﹕∠2﹕∠3﹕∠4=1﹕2﹕3﹕4，则∠1= 度.‎ ‎9．两点之间线段的 ，叫做这两点之间的距离.‎ ‎10．如图2所示，能用一个字母表示的角有_____个，以A为顶点的角有_____个，图中所有的角有_____个. ‎ ‎1‎ ‎4‎ ‎2‎ ‎3‎ ‎ 图1 图2 图3‎ ‎11．如图3，∠AOC=∠COD=∠BOD，则OD平分______，OC平分______，‎ ‎∠AOB =___________=__ ____.‎ ‎12．8点30分，分针和时针之间的夹角的度数是 °.‎ ‎13．过平面内一点能画 条直线，过平面内两点P、Q能画 条直线.‎ ‎14．如果一个角的度数为，则它的补角为__ ____，余角为___ ___.‎ ‎15．已知，∠的补角为125°，∠的余角为37°,则、的大小关系为_____.‎ ‎16.如图4，∠EOF=∠AOD=∠BOD=Rt∠，则图中与∠AOF互余的角有 ，与∠BOE互补的角有 . ‎ ‎ 17．如图5，AB⊥MN，CD⊥MN，已知∠1=α，∠2=β，∠3=3α-β，则α= 度，‎ E D C B A F E C A N M D B O F D A B ‎3‎ ‎2‎ ‎1‎ β= 度. ‎ 图4 图5 图6 ‎ ‎ 18．如图6，AC⊥BC，垂足为C，CD⊥AB，垂足为D；‎ 则（1）点A到直线BC的距离是 ；‎ ‎ （2）点B到直线AC的距离是 ；‎ ‎（3）点C到直线AB的距离是 . ‎ ‎ 19．已知点C分线段AB为5﹕7，点D分线段AB为5﹕11，CD=‎10cm,则AC= ，‎ D C A B ‎1‎ ‎5‎ ‎4‎ ‎3‎ ‎2‎ BC= ，AB= . ‎ ‎ 20．如右图，若∠1=∠2，则可判定的平行线 ‎ 是 ；若AC⊥BD且AB∥DC，则 ‎∠3与∠4的关系是 ，∠3与 ‎∠5的的关系是 . ‎ 一、 选择题（每小题2分，共12分）‎ ‎ 21．图中是对顶角的有 （ ）‎ ‎2‎ ‎1‎ ‎1‎ ‎1‎ ‎ ‎ ‎2‎ ‎2‎ ‎2‎ ‎1‎ ‎ ① ② ③ ④‎ A.① ② B.② ③ C.④ D.都不是 ‎ 22．下列语句中，那一句不是命题 （ ）‎ A. 两直线相交，只有一个交点； B. 在直线AB上除A、B外任取一点C；‎ C. 同位角相等，两直线平行； D. 内错角相等.‎ ‎23．经过A、B、C三点可连结直线的条数为 （ ）‎ A. 只能一条 B. 只能三条 C. 三条或一条 D. 不能确定 ‎24．如果直线∥，∥那么 （ ）‎ A. ∥ B. ⊥ C. = D. 以上都对 ‎25．下列语句中正确的是 （ ）‎ A. 过任意一点有且只有一条直线与已知直线垂直 ；‎ B. 必须过直线外一点有且只有一条直线与已知直线相交；‎ C. 必须经过直线上一点有且只有一条直线与已知直线垂直； ‎ D. 以上说法都不对.‎ ‎26．线段AB＝5，BC＝4，那么A、C两点的距离是 （ ）‎ A．1 B. ‎9‎ C. 1 或9 D. 以上答案都不对 ‎ 一、 解答题（每小题7分，共28分）‎ ‎ 27．一个角的余角与它的补角的和等于这个角的4倍，则这个角是多少度？‎ ‎28．如图，已知∠AOC=m°,∠BOD=n°,∠AOD=p°,求α、β、γ的度数.‎ D C B A O γ β α ‎29．如图，已知：BE平分∠ABC，CE平分∠BCD，且∠1+∠2=90°，‎ D C 求证：AB∥CD.‎ ‎2‎ E ‎1‎ B A ‎30．如图：已知点O是直线AE上一点，OB平分∠AOC，OD平分∠COE.‎ ‎①试写出∠COD的余角和∠AOD的补角.‎ ‎②若∠AOC﹕∠COE=4﹕5，求∠AOB的度数？‎ 二、三角形 一、填空（每题分，共分）‎ ‎．在中，则= ___________度．‎ ‎．在中，AB=AC，D是BA延长线上的一点，若则_____度．‎ ‎．某三角形的三边长分别是‎3cm、‎4cm、‎5cm，则它的面积是__________________．‎ ‎．如果一个三角形的周长为，三边之比为，则三边分别为______________．‎ ‎．若三角形的三个内角之比为，且最小边长为，则最长边长是_______．‎ ‎．在中，，AB=2BC，则= _____________度．‎ ‎．全等三角形的对应角相等＂的逆命题是_________________________________，　这个命题是_____命题（填＂真＂或＂假＂）‎ ‎．在中，、分别是、的中点，若米，则_____米．‎ ‎．已知、是的中线，、相交于点，，则_____．‎ ‎．若在和中， ，，，，，若和全等，则__________．　‎ ‎．若，，，，则 ．‎ 二、选择题（每小题分，共分）‎ ‎．下列命题是真命题的是（　　　）‎ Ａ．所有的等边三角形都全等；‎ Ｂ．所有的等腰直角三角形都全等；‎ Ｃ．两边分别相等的两个直角三角形全等；‎ Ｄ．关于一点中心对称的两个三角形全等．‎ ‎．点F是的重心，则点是的（　　　）‎ Ａ．三个内角平分线的交点；‎ Ｂ．三边中线的交点；‎ Ｃ．三边上的高的交点；‎ Ｄ．三边的垂直平分线的交点．‎ ‎．有两根棒，它们的长分别是和 ‎，若要钉成一个三角形木架，则在下列四根木棒中应该选取（　　　）‎ Ａ．．　　Ｂ．．　　Ｃ．．　Ｄ．．‎ ‎．下列条件中，不能判定两个三角形全等的是（　　　）‎ Ａ．已知三边对应相等；‎ Ｂ．已知两角和夹边对应相等；‎ Ｃ．已知两边和夹角对应相等；‎ Ｄ．已知两边和其中一边的对角对应相等． ‎ 三、简答题（每题分，共分）‎ ‎．如图：已知、分别在、上，，，求证：．‎ ‎．如图：已知，，求证：垂直平分．‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　‎ ‎．如图：已知，，求证：．‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　‎ ‎．如图：在中，，，是斜边的中点，点、分别在边、上，且，求证：是等腰三角形．‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　‎ 三、四边形 一．填空（2分×30＝分） A D ‎1在平行四边形 ABCD中，∠A=50°,则∠B= 0 ）‎ ‎2在平行四边形ABCD中，如果∠A=2∠B，则∠C= 0 B （3） C ‎3在平行四边形ABCD中，对角线AC、BD相交于O，则右上图中相等线段有 对。‎ ‎4平行四边形ABCD的周长为‎36cm，AB=‎8cm，则BC= cm。‎ ‎5平行四边形ABCD的周长是‎28cm，△ABC周长是‎20cm，则AC= cm ‎6对角线互相平分且相等的四边形是 形 ‎7已知矩形一条对角线长‎8cm，两条对角线的一个交角是60°，则矩形的边长为 cm ‎8已知菱形的两条对角线长分别为‎6cm和‎8cm，则菱形周长为 cm D C ‎9正方形的边长为m，则它的对角线长是 ‎ A (10) B E ‎ ‎10如图，正方形ABCD，延长AB至E，使BE=BD，则∠CDE= ‎ ‎11已知菱形相邻两角之比为1：2，周长为‎24cm，则较长对角线为 cm ‎ ‎12有一组邻边相等的平行四边形是 ‎ ‎13平行四边形ABCD的周长为‎20cm，它的两条高分别为2cm和3cm，则它的面积是 ‎ cm2 ‎ ‎14如图，矩形ABCD中，BC=2CD，在AD上取F点，使BF=BC，则∠FCD= ‎ ‎15梯形上、下两底长分别为‎4cm和‎6cm，则梯形的中位线长 cm ‎16如果直角梯形的一条对角线把这个梯形分成两个三角形，且其中一个是边长为‎6cm的等边三角形，那么这个梯形的面积是 cm2 ‎ A F D ‎ ‎17等腰梯形一个角为45°，高为2，上底为1，则中位线长 ‎ ‎18等腰梯形周长为‎80cm，中位线与腰长相等，则中位线等于 cm B （14） C ‎19梯形上底长‎3cm，下底长‎7cm，梯形被中位线分成的两部分的面积比是 。‎ ‎20等腰三角形是轴对称图形，对称轴是 。‎ ‎21过平行四边形的115°角的顶点作平行四边形的两条高，则这两条边的夹角的度数是 。‎ ‎22梯形ABCD中，AD∥BC，对角线AC、BD交于O，则图中面积相等的三角形有 对。‎ ‎23一个正方形的面积是4厘米2，这个正方形的一条对角线的长是 厘米。‎ A D ‎24菱形一组邻角之比为1：5，且周长为‎8cm,则它的面积为 cm2。 O ‎25平行四边形是中心对称图形,对称中心是 。‎ ‎ B C ‎26正方形的对称轴有 条。‎ ‎27梯形上、下两底长分别为‎3cm和‎5cm，则连接梯形两对角线中点的线段长 cm (22)‎ ‎28有一个角是直角的 形是正方形。‎ ‎29矩形ABCD对角线交于点O，一条边AB长为‎1cm，△AOB是正三角形，则矩形的周长是 cm。‎ ‎30直角梯形中位线长为a，一腰长为b，这条腰与底所成的角是30°，则它的面积是 ‎ 二、 选择题（2分×10=20分）‎ ‎1、平行四边形ABCD的对角线AC、BD交于O，则图中全等三角形共有 （ ）‎ ‎（A）1对 （B）2对 （C）3对 （D）4对 ‎2、平行四边形两邻边长分别为‎6cm和‎4cm，且他们的夹角为60°，则它的面积为 （ ）‎ ‎（A）12 cm2 （B）7cm2 （C）6cm2 （D）4cm2 ‎ ‎3、四边形的两条对角线互相垂直，这个四边形是 （ ）‎ ‎（A）矩形 （B）菱形 （C）正方形 （D）形状不确定 ‎4、菱形具有而矩形不一定具有的性质是 （ ）‎ ‎（A）对角线平分一组对角 （B）对角线互相平分 ‎（C）对角相等 （D）对边平行且相等 ‎5、菱形的周长是‎40cm，一条对角线长‎16cm，则它的面积 （ ）‎ ‎（A）‎192cm2 （B）‎96cm2 （C）‎48cm2 （D）‎40cm2‎ ‎6、能判定四边形ABCD是平行四边形的是 （ ）‎ ‎（A）AB∥CD，AD∥BC （B）∠A=∠B，∠C=∠D ‎（C）AB=AD，CB=CD （D）AB∥CD，AD=BC ‎7、下列图形中，既是轴对称，又是中心对称的图形是 （ ）‎ ‎（A）平行四边形 （B）等腰梯形 （C）菱形 （D）角 ‎8、下列图形中，一定有外接圆的是 （ ）‎ ‎（A）四边形 （B）矩形 （C）平行四边形 （D）梯形 ‎9、平行四边形一条边长14，下列各组数中能分别作出它的两条对角线的长的是 （ ）‎ ‎（A）10和16 （B）12和16 （C）20和22 （D）10和40‎ ‎10、一组对边平行，而另一组对边相等的四边形是 （ ）‎ ‎（A）平行四边形 （B）矩形 （C）等腰梯形 （D）平行四边形或等腰梯形 ‎ 三、简答题 1、 已知四边形ABCD中，AB=DC，AE⊥BD，CF⊥BD，垂足分别为E、F，AE=CF；‎ 求证：四边形ABCD是平行四边形.‎ ‎ D C ‎ E ‎ F ‎ A B ‎2、如图：等腰梯形ABCD中，AB=CD，∠B=45°，AD+BC=30，高AE=7，求梯形两底AD，BC的长。‎ ‎ A D ‎ B E C ‎3、如图，平行四边形ABCD中，E是BC上一点，AE交BD于点F，已知BE：EC=4：1,S△BEF=48‎ 求：S△FDA ‎ A D ‎ F ‎ B E C ‎4、如图，在正方形ABCD中，E是DC的中点，F是BC上的点，CF=BC 求证：AE平分∠DAF ‎ ‎ A D ‎ E ‎ B F C 五、比例线段和相似形 一、填空题（每题3分，共36分）‎ ‎1.若线段b是线段a和c的比例中项,且a=‎4cm,c=‎9cm，则b= ‎ ‎2.如果地图上A、B两地的图距是‎4cm,表示的实际距离为160公里,则实际距离为400公里的两地，在地图上的图距为 ‎ ‎3.已知，线段AB=‎1cm,C是AB的黄金分割点,且AC＞BC，则AC= ‎ ‎4.如图，DE∥BC，BD=2AD，DE=2，则BC= ‎ ‎5.如图，在△ABC中，DE∥BC，，BC=4，则DE= ‎ ‎6.如图，G是的△ABC重心,EF过G且EF∥BC,若BC=2,则EF= ‎ A ‎ ‎A B C D E ‎5题 B C E ‎6题 G A B C D E ‎4题 F ‎7.两个相似三角形对应角平分线的比为3∶4,则周长的比为 ‎ ‎8.如图,E、F分别在AC、BC上,若AE=3，AC=7，FC=3.2，BC=5.6,则EF与AB (填平行或不平行)‎ ‎9.一个直角三角形的两边长分别是3和6,另一个直角三角形的两边长分别是2和4,那么这两个三角形 相似。（填“一定”，“不一定”或“一定不”）‎ ‎10.如图,在梯形ABCD中,AD∥BC，EF∥BC，AD=2，BC=8，且DF∶FC=2∶3，则EF= ‎ A B C E F A B C D F E C A B E D ‎8题 ‎10题 ‎12题 ‎11.在△ABC中,AC=6，BC=9，在BC上取一点D,使△ABC∽△DAC,则BD=‎ ‎12.如图CD是Rt△ABC斜边上的高,若AD=6，BD=2，CE=3，则BE= ‎ 二、选择题（每题3分，共12分）‎ ‎13.如图，能推得DE∥BC的条件是（ ）‎ A.AD∶AB=DE∶BC；B.AD∶DB=DE∶BC；C.AD∶DB=AE∶EC；D.AE∶AC=DE∶BC.‎ ‎14.如图，AG∥BD，AF∶FB=2∶5，BC∶CD=4∶1，AG=4，则CD=（ ）‎ A G D B C F ‎（14题）‎ AA B C D E ‎（13题）‎ .1； B.2； C.3； D.4.‎ ‎15.下列命题错误的是（ ）‎ A.相似三角形周长之比等于对应高之比；B.两个等腰直角三角形一定相似；‎ C.各有一个角等于的两个等腰三角形相似；‎ D.两边对应成比例且有一个角相等的两个三角形相似 ‎16.顺次连接三角形各边中点，所成的三角形的高与原三角形对应高之比为（ ）‎ A. 2∶1； B. 1∶2； C. 1∶4； D. 4∶1.‎ 三、简答题（每题10分，共40分）‎ ‎17.已知，EF∥AB，ED=DF，AF交BC于G，求证：‎ A B C E F G D ‎18.如图，ABCD为正方形，过A一条直线依次与BD、DC及BC的延长线交于点E、F、G，AE=‎5cm，EF=‎4cm，求FG。‎ A B C D G E F ‎19.如图，△ABC中，AD、BE是BC、AC边上的高，连接DE，求证：△DEC∽△ABC.‎ A B C D E ‎20.如图，G是△ABC的重心，AG、BG的延长线分别交BC于F，交AC于E，已知，求：①；②‎ A B C E F G 四、解答题（12分）‎ ‎21.在△FEC中，∠ACB=，AC=BC，∠ECF=，BE=x，BF=y。‎ ‎（1）求证：∠ECA=∠F；‎ ‎（2）若AE=2，求y与x的函数关系式 C E F A B 六、圆 一、 填空（每小题3分，共48分）‎ 1． 圆心的坐标是（3，4），半径是5，那么坐标原点在————————（填圆内或圆上或圆外）.‎ 1． 已知⊙O的半径是5，圆心O到一条直线的距离是4，那么这条直线和圆的公共点的个数是———————— .‎ 2． 如果⊙O和⊙Oˊ的半径分别为‎4cm和‎3cm，OOˊ=‎15cm,那么⊙O和⊙Oˊ的位置关系是———————— .‎ 3． ‎⊙O的一条弦长为8，弦心距为3，则⊙O的直径长为———————— .‎ 4． 如果⊙O和⊙Oˊ相交，两圆的半径分别是3和5，那么OOˊ长的范围是———————— .‎ 5． 如果⊙O和⊙O1相切，⊙O的半径是3，圆心距OO1=5，则⊙O1的半径等于———————— . ‎ 6． 已知AB是⊙O的直径，CD是弦，EC⊥CD，FD⊥CD，E、F在AB上，OG⊥CD，G为垂足，已知EC=3，FD=5，则OG=———————— .‎ 7． 在Rt△ABC中，∠C=90°，如果AB=5，BC=3，那么△ABC的内切圆的半径=———————— .‎ 8． 过⊙O外一点P，向⊙O作切线PA、PB，A、B为切点，如果⊙O的半径是‎4cm，PO=‎8cm,那么△PAB是————————三角形.‎ ‎10.已知P是⊙O外一点，如果⊙O的半径为3，PO=5，那么点P到圆O的切线长为———————— .‎ ‎11.正八边形的中心角等于————————度 .‎ ‎12.如果正六边形边长为a，那么面积等于———————— .‎ ‎13.已知两等圆半径为‎5cm，公共弦长为‎6cm，则圆心距为————————cm .‎ ‎14.若⊙O的直径为，则⊙O的内接正方形的边长为———————— .‎ ‎15.半径分别为1、2、3的三圆两两外切，那么以三个圆心为顶点构成的三角形的形状是———————— .‎ ‎16.同圆的内接正三角形和外切正三角形的边长的比是———————— .‎ 二． 选择题（每小题3分，共18分）‎ ‎17．到三角形各边距离相等的点是这个三角形的 （ ）‎ ‎（A）外心； （B）内心； （C）重心； （D）垂心.‎ ‎18．在Rt△ABC中，∠C=90°，BC=6，AB=10，如果以点C为圆心，画圆与AB相切，那么圆C的半径是 （ ）‎ ‎（A）2.4； （B） 3.6； （C） 4.8； （D） 5.‎ ‎19．如果两个圆有且只有一条公切线，那么这两个圆的位置关系是 （ ）‎ ‎（A）外切； （B）相交； （C）内切； （D）内含.‎ ‎20．两圆半径的比为5∶2，当两圆外切时圆心距为7，此时外公切线长为 （ ）‎ ‎（A）4； （B）2； （C）7； （D）.‎ ‎21．下列命题中，正确的是 （ ）‎ ‎（A）垂直于半径的直线是这圆的切线； （B）平分弦的直径垂直于弦；‎ ‎（C）任何两个圆必有两条外公切线； ‎ ‎ （D）经过半径外端且垂直于这条半径的直线是圆的切线.‎ ‎22．已知△ABC的周长是24，内切圆半径是1.5，那么这个三角形的面积是 （ ）‎ ‎（A）24； （B）20； （C）18； （D）16.‎ 三．简答题（23、24题每题11分，第25题12分，共34分）‎ ‎23如图，Rt△ABC中，∠BAC=90°，AC=5，AB=12，圆心O在AB上，⊙O过点A，且与BC相切于D，求⊙O的半径.‎ ‎24如图，以AB为直径的⊙O上有一点C，CD切⊙O于点C，AE⊥CD，D为垂足，BC的延长线交AE于点E；求证：△ABE是等腰三角形. ‎ ‎25.如图，⊙O1和⊙O2的半径都是2，相交于点A和B，⊙O1过点O2，⊙O2过点O1，‎ （1） 求证：四边形AO1BO2是菱形；‎ （2） 求菱形AO1BO2的面积.‎