2018中考数学统计与概率专题训练 19页

‎2018中考数学专题训练：统计 ‎1. （2012福建）“六•一”前夕质监部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品，以下是根据抽查结果绘制出的不完整的统计表和扇形图； ‎ 类别 儿童玩具 童车 童装 抽查件数 ‎90‎ 请根据上述统计表和扇形提供的信息，完成下列问题：‎ ‎（1）分别补全上述统计表和统计图；‎ ‎（2）已知所抽查的儿童玩具、童车、童车的合格率为90%、85%、80%，若从该超市的这三类儿童用品中随机购买一件，请估计购买到合格品的概率是多少？ ‎ ‎【答案】解：（1）童车的数量是300×25%=75，童装的数量是300－75－90=135；‎ 儿童玩具占得百分比是（90÷300）×100%=30%。童装占得百分比1－30%－25%=45%。‎ 补全统计表和统计图如下：‎ 类别 儿童玩具 童车 童装 抽查件数 ‎90‎ ‎75‎ ‎135‎ ‎（2）∵儿童玩具中合格的数量是90×90%=81，童车中合格的数量是 19‎ ‎75×85%=63.75，童装中合格的数量是135×80%=108，‎ ‎∴从该超市的这三类儿童用品中随机购买一件，购买到合格品的概率是 ‎。‎ ‎2. （2012湖北） “端午节”是我国的传统佳节，民间历来有吃“粽子”的习俗．我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽（以下分别用A、B、C、D表示）这四种不同口味粽子的喜爱情况，在节前对某居民区市民进行了抽样调查，并将调查情况绘制成如下两幅统计图（尚不完整）．‎ 请根据以上信息回答：‎ ‎（1）本次参加抽样调查的居民有多少人？‎ ‎（2）将两幅不完整的图补充完整；‎ ‎（3）若居民区有8000人，请估计爱吃D粽的人数；‎ ‎（4）若有外型完全相同的A、B、C、D粽各一个，煮熟后，小王吃了两个．用列表或画树状图的方法，求他第二个吃到的恰好是C粽的概率．‎ ‎【答案】解：（1）60÷10%=600（人）．‎ 答：本次参加抽样调查的居民有600人。‎ ‎（2）喜爱C粽的人数：600－180－60－240=120，频率：120÷600=20%；‎ ‎ 喜爱A粽的频率：180÷600=30%。‎ ‎ 据此补充两幅统计图如图： ‎ 19‎ ‎（3）8000×40%=3200（人）．‎ 答：该居民区有8000人，估计爱吃D粽的人有3200人。‎ ‎（4）画树状图如下：‎ ‎ ∵共有12种等可能结果，第二个吃到的恰好是C粽的情况有3种，‎ ‎ ∴第二个吃到的恰好是C粽的概率是。‎ ‎ 答：他第二个吃到的恰好是C粽的概率是。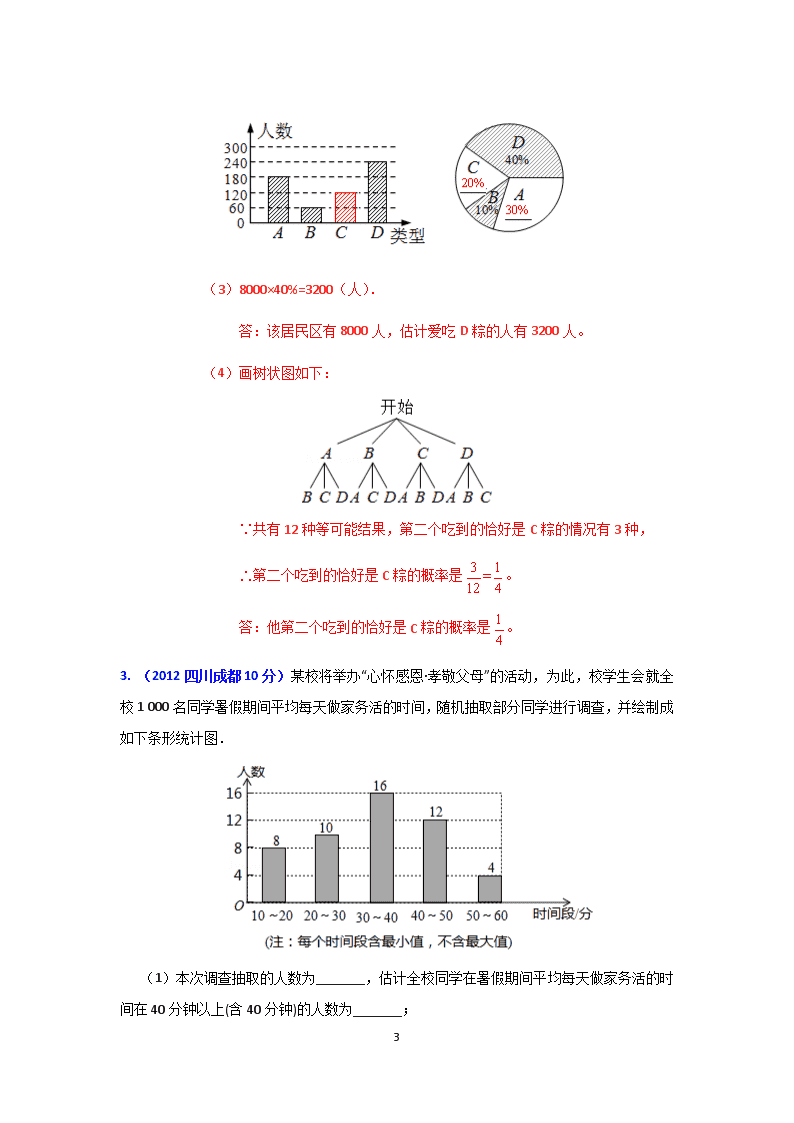‎ ‎3. （2012四川成都10分）某校将举办“心怀感恩·孝敬父母”的活动，为此，校学生会就全校1 000名同学暑假期间平均每天做家务活的时间，随机抽取部分同学进行调查，并绘制成如下条形统计图．‎ ‎ （1）本次调查抽取的人数为_______，估计全校同学在暑假期间平均每天做家务活的时间在40分钟以上(含40分钟)的人数为_______；‎ 19‎ ‎ （2）校学生会拟在表现突出的甲、乙、丙、丁四名同学中，随机抽取两名同学向全校汇报．请用树状图或列表法表示出所有可能的结果，并求恰好抽到甲、乙两名同学的概率．‎ ‎【答案】解：（1）50；320。‎ ‎ （2）列表如下：‎ ‎∵共有12种情况，恰好抽到甲、乙两名同学的是2种，‎ ‎∴P（恰好抽到甲、乙两名同学）=。‎ ‎【考点】频数分布直方图，用样本估计总体，列表法或树状图法，概率。‎ ‎【分析】（1）把各时间段的学生人数相加即可：8+10+16+12+4=50（人）；用全校同学的人数乘以40分钟以上（含40分钟）的人数所占的比重，计算即可得解：1000×（人）。‎ ‎（2）列表或画树状图，然后根据概率公式计算即可得解。‎ ‎4. （2012四川宜宾8分）为了解学生的艺术特长发展情况，某校音乐组决定围绕“在舞蹈、乐器、声乐、戏曲、其它活动项目中，你最喜欢哪一项活动（每人只限一项）”的问题，在全校范围内随机抽取部分学生进行问卷调查，并将调查结果绘制成如下两幅不完整的统计图．‎ 19‎ 请你根据统计图解答下列问题：‎ ‎（1）在这次调查中一共抽查了 名学生，其中，喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为 ，喜欢“戏曲”活动项目的人数是 人；‎ ‎（2）若在“舞蹈、乐器、声乐、戏曲”活动项目任选两项设立课外兴趣小组，请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项活动的概率．‎ ‎【答案】解：（1）50；24%；4。‎ ‎（2）设舞蹈、乐器、声乐、戏曲的序号依次是①②③④，画树状图： ‎ ‎ ∵任选两项设立课外兴趣小组， 共有12种等可能结果，故恰好选中“舞蹈、声乐”两项活动的有2种情况，‎ ‎∴故恰好选中“舞蹈、声乐”两项活动的概率是。‎ ‎5. （2012四川）某校八年级为了解学生课堂发言情况，随机抽取该年级部分学生，对他们某天在课堂上发言的次数进行了统计，其结果如下表，并绘制了如图10所示的两幅不完整的统计图，已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题：‎ （1） 求出样本容量，并补全直方图；‎ （2） 该年级共有学生500人，请估计全年级在这天里发言次数不少于12的次数；‎ 19‎ （1） 已知A组发言的学生中恰有1位女生，E组发言的学生中有2位男生，现从A组与E组中分别抽一位学生写报告，请用列表法或画树状图的方法，求所抽的两位学生恰好是一男一女的概率。‎ ‎【答案】解：（1）∵由发言人数直方图可知B组发言人为10人，又已知B、E两组发言人数的比为5:2，‎ ‎ ∴E组发言人为4人。 ‎ 又∵由发言人数扇形统计图可知E组为8％，∴发言人总数为4÷8%=50人。‎ ‎∴由扇形统计图知A组、C组、D组分别为3人，15人，13人。‎ ‎∴F组为50－3－10－15－13－4=5人。‎ ‎∴样本容量为50人。补全直方图为：‎ ‎(2) ∵在统计的50人中，发言次数大于12的有4＋5=9人，‎ ‎∴在这天里发言次数不少于12的频率为9÷50=18%。‎ 19‎ ‎∴全年级500人中，在这天里发言次数不少于12的次数为500×18%=90（次）。‎ ‎（3）∵A组发言的学生为3人，∴有1位女生，2位男生。‎ ‎∵E组发言的学生： 4人，∴有2位女生，2位男生。‎ ‎∴由题意可画树状图为：‎ ‎∴共有12种情况，所抽的两位学生恰好是一男一女的情况有6种，‎ ‎∴所抽的两位学生恰好是一男一女的概率为。‎ ‎6. （2012辽宁）某中学对本校500名毕业生中考体育加试测试情况进行调查，根据男生1000‎ 米及女生800米测试成绩整理、绘制成如下不完整的统计图（图①、图②），请根据统计图提供的信息，‎ 回答下列问题：‎ ‎（1）该校毕业生中男生有 ▲ 人，女生有 ▲ 人；‎ ‎（2）扇形统计图中a= ▲ ,b= ▲ ；‎ ‎（3）补全条形统计图（不必写出计算过程）；‎ ‎（4）若本校500名毕业生中随机抽取一名学生，这名学生该项测试成绩在8分以下的概率是多少？‎ 19‎ ‎【答案】解：（1）300；200。‎ ‎（2）12；62。‎ ‎（3）补图如图所示：‎ ‎（4）随机抽取的学生的测试成绩在8分以下的概率是10%。‎ ‎7. （2012六盘水）假期，六盘水市教育局组织部分教师分别到A．B．C．D四个地方进行新课程培训，教育局按定额购买了前往四地的车票．如图1是未制作完成的车票种类和数量的条形统计图，请根据统计图回答下列问题：‎ 19‎ ‎（1）若去C地的车票占全部车票的30%，则去C地的车票数量是 张，补全统计图．‎ ‎（2）若教育局采用随机抽取的方式分发车票，每人一张（所有车票的形状、大小、质地完全相同且充分洗匀），那么余老师抽到去B地的概率是多少？‎ ‎（3）若有一张去A地的车票，张老师和李老师都想要，决定采取旋转转盘的方式来确定．其中甲转盘被分成四等份且标有数字1、2、3、4，乙转盘分成三等份且标有数字7、8、9，如图2所示．具体规定是：同时转动两个转盘，当指针指向的两个数字之和是偶数时，票给李老师，否则票给张老师（指针指在线上重转）．试用“列表法”或“树状图”的方法分析这个规定对双方是否公平．‎ ‎【答案】解：（1）30。补全统计图如下：‎ ‎（2）余老师抽到去B地的概率是。‎ ‎（3）根据题意列表如下：‎ ‎∵两个数字之和是偶数时的概率是。‎ ‎∴票给李老师的概率是。‎ ‎∴这个规定对双方公平。‎ 19‎ ‎8. （2012新疆）为了解“阳光体育”活动情况，我市教育部门在市三中2000名学生中，随机抽取了若干学生进行问卷调查（要求每位学生只能填写一种自己喜欢的活动），并将调查的结果绘制成如图的两幅不完整的统计图：‎ 根据以上信息解答下列问题：‎ ‎（1）参加调查的人数共有　 　人；在扇形图中，表示“C”的扇形的圆心角为　 　度；‎ ‎（2）补全条形统计图，并计算扇形统计图中的m；‎ ‎（3）若要从该校喜欢“B”项目的学生中随机选择100名，则喜欢该项目的小华同学被选中的概率是多少？‎ ‎【答案】解：（1）300；108。‎ ‎（2）∵抽取的学生中喜欢“C”项目的学生数为300－60－69－36－45=90（人）。‎ ‎ ∴补全条形统计图如下：‎ ‎∵m%=×100%=20%，∴m=20。‎ ‎（3）喜欢B项目的有2000×=460（人），‎ 19‎ ‎∴小华被抽中的概率为。‎ ‎9. （2012青海）西宁市教育局自实施新课程改革后，学生的自主学习、合作交流能力有很大提 高．张老师为了了解所教班级学生自主学习、合作交流的具体情况，对本班部分学生进行了为期半个月的 跟踪调查，将调查结果分成四类：A—特别好、B—好、C—一般、D—较差，并将调查结果绘制成两幅不 完整的统计图．请你根据统计图解答下列问题：‎ ‎(1)本次调查中，张老师一共调查了 名同学；‎ ‎(2)将上面的条形统计图补充完整；‎ ‎(3)为了共同进步，张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习，‎ 请用列表或画树状图的方法列出所有等可能的结果，并求出所选两位同学恰好是一位男同学和一位女同学的概率．‎ ‎【答案】解：（1）20。‎ ‎（2）C组人数为：20×25%=5人，所以，女生人数为5-3=2人。‎ D组人数为：20×（1-15%-50%-25%）=20×10%=2人，所以，男生人数为2-1=1人。‎ 19‎ 补全统计图如图；‎ ‎（3）画树状图如图：‎ ‎∴所有等可能结果：男男、男女、女男、女女、女男、女女。‎ 又∵所选两位同学恰好是一位男同学和一位女同学的结果有3种，‎ ‎∴P（一男一女）=。‎ ‎10. （2012黑龙江牡丹江7分）在创建“绿色环境城市”活动中，某城市发布了一份2012年l至5月份空气质量抽样调查报告，随机抽查的30天中，空气质量的相关信息如下：‎ 空气污 染指数 ‎0～50‎ ‎51～100‎ ‎101～150‎ ‎151～200‎ ‎201～250‎ 空气质 量指数 优 良 轻微 污染 轻度 污染 中度 污染 天数 ‎6‎ ‎15‎ ‎3‎ ‎2‎ 19‎ ‎ 请根据图表解答下列问题(结果取整数)：‎ ‎ (1)请将图表补充完整；‎ ‎ (2)填空：根据抽样数据，估计该城市的空气质量级别为 的天数最多．‎ ‎ (3)请你根据抽样数据，通过计算，预测该城市一年(365天)中空气质量级别为优和良的天数共约有多少天 ‎ (4)请你根据数据显示，向有关部门提出一条创建“绿色环境城市”的建议．‎ ‎【答案】解：（1）将图表补充完整如下：‎ 空气污 染指数 ‎0～50‎ ‎51～100‎ ‎101～150‎ ‎151～200‎ ‎201～250‎ 空气质 量指数 优 良 轻微 污染 轻度 污染 中度 污染 天数 ‎6‎ ‎15‎ ‎4‎ ‎3‎ ‎2‎ 19‎ ‎ （2）良。‎ ‎ （3）∵365×（20%＋50%）≈256（天），‎ ‎ ∴预测该城市一年(365天)中空气质量级别为优和良的天数共约有256天。‎ ‎（4）①采用“绿色化学”工艺，使工业原料尽可能转化为所需要的物质；‎ ‎②推广使用乙醇汽油，减少有害气体的排放；‎ ‎③推广使用卫生的一次性发泡塑料餐具，方便居民生活；‎ ‎④增加绿化面积，建设生态园林城市。‎ 等等（一条即可，答案不唯一）。‎ ‎11. （2012黑龙江）学生的学习兴趣如何是每位教师非常关注的问题．为此，某校教师对该校部分学生的学习兴趣进行了一次抽样调查（把学生的学习兴趣分为三个层次，A层次：很感兴趣；B层次：较感兴趣；C层次：不感兴趣）；并将调查结果绘制成了图①和图②的统计图（不完整）．请你根据图中提供的信息，解答下列问题：‎ ‎（1）此次抽样调查中，共调查了200 名学生；‎ ‎（2）将图①、②补充完整；‎ ‎（3）将图②中C层次所在扇形的圆心角的度数；‎ ‎（4）根据抽样调查的结果，请你估计该校1200名学生中大约有多少名学生对学习感兴趣（包括A层次和B层次）． ‎ ‎【答案】解：（1）200。‎ 19‎ ‎（2）C层次的人数为：200-120-50=30（人）；所占的百分比是：30 200 ×100%=15%。‎ B层次的人数所占的百分比是1－25%－15%=60%。‎ ‎∴将图①、②补充完整如下：‎ ‎（3）C层次所在扇形的圆心角的度数是：360×15%=54°。‎ ‎（4）根据题意得：（25%+60%）×1200=1020（人）。‎ 答：估计该校1200名学生中大约有1020名学生对学习感兴趣。‎ ‎12. （2012广西贵港9分）某学校有1500名学生参加首届“我爱我们的课堂”为土主题的图片制作比赛，赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如下：‎ 频率分布统计表 频率分布直方图 分数段 频数 频率 ‎30‎ ‎0‎ ‎10‎ ‎50‎ ‎40‎ ‎20‎ ‎60‎ ‎70‎ ‎80‎ ‎90‎ ‎100‎ 分数/分 频数 ‎10‎ ‎35‎ ‎40‎ ‎60≤x＜70‎ ‎40‎ ‎0.40‎ ‎70≤x＜80‎ ‎35‎ b ‎80≤x＜90‎ a ‎0.15‎ ‎90≤x＜100‎ ‎10‎ ‎0.10‎ 请根据上述信息，解答下列问题：‎ ‎（1）表中：a＝___________，b＝___________；‎ 19‎ ‎（2）请补全频数分布直方图；‎ ‎（3）如果将比赛成绩80分以上（含80分）定为优秀，那么优秀率是多少？并且估算该校参赛学生获得 优秀的人数。‎ ‎【答案】解：（1）15；0.35。‎ ‎ （2）补全频数分布直方图如下：‎ ‎ （3）优秀率＝(0.15＋0.10)×100%＝25%。‎ ‎∵1500×25%＝375（人），‎ ‎∴估计该校参赛学生获得优秀的人数为375人。‎ ‎13. （2012贵州）近几年兴义市加大中职教育投入力度，取得了良好的社会效果。某校随机调查了九年级a名学生升学意向，并根据调查结果绘制如图的两幅不完整的统计图。‎ 请你根据图中信息解答下列问题：‎ ‎（1）a= ;[来源:学§科§网]‎ ‎（2）扇形统计图中，“职高”对应的扇形的圆心角α= ；‎ 19‎ ‎（3）请补全条形统计图；‎ ‎（4）若该校九年级有学生900名，估计该校共有多少名毕业生的升学意向是职高。‎ ‎【答案】解：（1）40。（2）108°。‎ ‎（3）∵普高：60%×40=24（人），职高：30%×40=12（人），∴补全条形统计图如图：‎ ‎（4）∵900×30%=270（名），‎ ‎∴该校共有270名毕业生的升学意向是职高。‎ ‎14. （2012北京） 某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量，如下表所示：‎ 用电量（度）‎ ‎120‎ ‎140‎ ‎160‎ ‎180‎ ‎200‎ 户数 ‎2‎ ‎3‎ ‎6‎ ‎7‎ ‎2‎ 则这20户家庭该月用电量的众数和中位数分别是【 】‎ A．180，160 B．160，180 C．160，160 D．180，180‎ ‎【答案】A。‎ ‎15. （2012江苏）甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.4环,‎ 方差分别是,,,.在本次射击测试中,成绩最稳定的是【 】‎ ‎ A．甲 B．乙 C．丙 D．丁 19‎ ‎【答案】C。‎ ‎16. （2012湖北）对于一组统计数据：2，3，6，9，3，7，下列说法错误的是【 】‎ A．众数是3 B．中位数是6 C．平均数是5 D．极差是7‎ ‎【答案】B。‎ ‎17. （2012湖北恩施3分）希望中学开展以“我最喜欢的职业”为主题的调查活动，通过对学生的随机抽样调查得到一组数据，如图是根据这组数据绘制的不完整的统计图，则下列说法中，不正确的是【 】‎ ‎ A．被调查的学生有200人 B．被调查的学生中喜欢教师职业的有40人 ‎　 C．被调查的学生中喜欢其他职业的占40% D．扇形图中，公务员部分所对应的圆心角为72°‎ ‎【答案】C。‎ ‎18. （2012内蒙古赤峰10分）甲、乙两名运动员在相同的条件下各射靶10次，每次射靶的成绩情况如图所示：‎ 19‎ ‎（1）请你根据图中数据填写下表：‎ 运动员 平均数 中位数 方差 甲 ‎7‎ ‎7‎ 乙 ‎7‎ ‎2.6‎ ‎（2）根据以上信息分析谁的成绩好些．‎ ‎【答案】解：（1）填表如下：‎ 运动员 平均数 中位数 方差 甲 ‎7‎ ‎7‎ ‎1‎ 乙 ‎7‎ ‎7‎ ‎2.6‎ ‎（2）因为甲、乙的平均数与中位数都相同，甲的方差小，所以更稳定，因此甲的成绩好些。‎ 19‎