2020年四川省凉山州中考数学试卷(含解析） 23页

‎2020年四川省凉山州中考数学试卷 一、选择题（本大题共12小题，每小题4分，共48分）在每小题给出的四个选项中只有一项是正确的，把正确选项的字母填涂在答题卡上相应的位置．‎ ‎1．（4分）﹣12020＝（　　）‎ A．1 B．﹣1 C．2020 D．﹣2020‎ ‎2．（4分）如图，下列几何体的左视图不是矩形的是（　　）‎ A． B． C． D．‎ ‎3．（4分）点P （2，3）关于x轴对称的点P'的坐标是（　　）‎ A．（2，﹣3） B．（﹣2，3） C．（﹣2，﹣3） D．（3，2）‎ ‎4．（4分）已知一组数据1，0，3，﹣1，x，2，3的平均数是1，则这组数据的众数是（　　）‎ A．﹣1 B．3 C．﹣1和3 D．1和3‎ ‎5．（4分）一元二次方程x2＝2x的根为（　　）‎ A．x＝0 B．x＝2 C．x＝0或x＝2 D．x＝0或x＝﹣2‎ ‎6．（4分）下列等式成立的是（　　）‎ A．‎81‎‎=‎±9 B．|‎5‎‎-‎2|‎=-‎5‎+‎2 ‎ C．（‎-‎‎1‎‎2‎）﹣1＝﹣2 D．（tan45°﹣1）0＝1‎ ‎7．（4分）若一次函数y＝（2m+1）x+m﹣3的图象不经过第二象限，则m的取值范围是（　　）‎ A．m‎＞-‎‎1‎‎2‎ B．m＜3 C．‎-‎1‎‎2‎＜‎m＜3 D．‎-‎1‎‎2‎＜‎m≤3‎ ‎8．（4分）点C是线段AB的中点，点D是线段AC的三等分点．若线段AB＝12cm，则线段BD的长为（　　）‎ A．10cm B．8cm C．10cm 或8cm D．2cm 或4cm ‎9．（4分）下列命题是真命题的是（　　）‎ A．顶点在圆上的角叫圆周角 ‎ B．三点确定一个圆 ‎ C．圆的切线垂直于半径 ‎ D．三角形的内心到三角形三边的距离相等 第23页（共23页）‎ ‎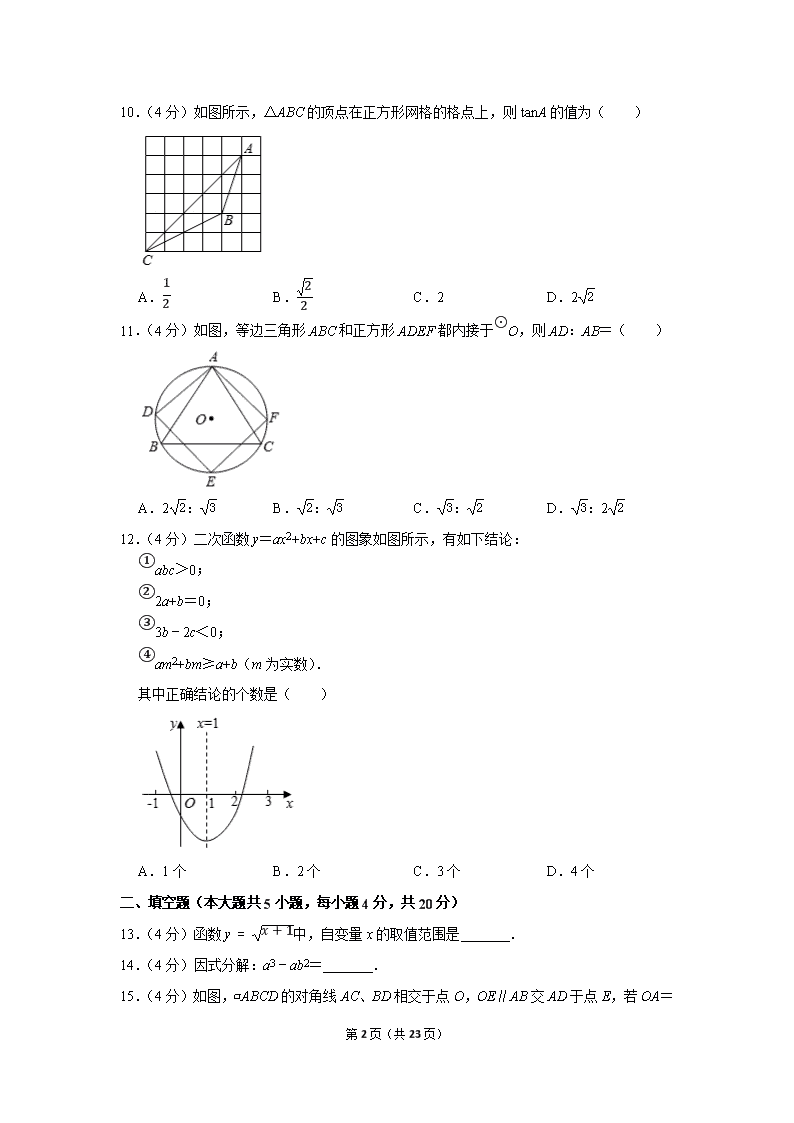10．（4分）如图所示，△ABC的顶点在正方形网格的格点上，则tanA的值为（　　）‎ A．‎1‎‎2‎ B．‎2‎‎2‎ C．2 D．2‎‎2‎ ‎11．（4分）如图，等边三角形ABC和正方形ADEF都内接于⊙O，则AD：AB＝（　　）‎ A．2‎2‎：‎3‎ B．‎2‎：‎3‎ C．‎3‎：‎2‎ D．‎3‎：2‎‎2‎ ‎12．（4分）二次函数y＝ax2+bx+c的图象如图所示，有如下结论：‎ ‎①abc＞0；‎ ‎②2a+b＝0；‎ ‎③3b﹣2c＜0；‎ ‎④am2+bm≥a+b（m为实数）．‎ 其中正确结论的个数是（　　）‎ A．1个 B．2个 C．3个 D．4个 二、填空题（本大题共5小题，每小题4分，共20分）‎ ‎13．（4分）函数y‎=‎x+1‎中，自变量x的取值范围是　 　．‎ ‎14．（4分）因式分解：a3﹣ab2＝　 　．‎ ‎15．（4分）如图，▱ABCD的对角线AC、BD相交于点O，OE∥AB交AD于点E，若OA＝‎ 第23页（共23页）‎ ‎1，△AOE的周长等于5，则▱ABCD的周长等于　 　．‎ ‎16．（4分）如图，点C、D分别是半圆AOB上的三等分点，若阴影部分的面积是‎3‎‎2‎π，则半圆的半径OA的长为　 　．‎ ‎17．（4分）如图，矩形OABC的面积为‎100‎‎3‎，对角线OB与双曲线y‎=‎kx（k＞0，x＞0）相交于点D，且OB：OD＝5：3，则k的值为　 　．‎ 三、解答题（本大题共5小题，共32分）解答应写出文字说明、证明过程或演算步骤．‎ ‎18．（5分）解方程：x‎-x-2‎‎2‎=‎1‎+‎‎2x-1‎‎3‎．‎ ‎19．（5分）化简求值：（2x+3）（2x﹣3）﹣（x+2）2+4（x+3），其中x‎=‎‎2‎．‎ ‎20．（7分）如图，一块材料的形状是锐角三角形ABC，边BC＝120mm，高AD＝80mm，把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是多少？‎ ‎21．（7分）某校团委在“五•四”青年节举办了一次“我的中国梦”作文大赛，分三批对全 第23页（共23页）‎ 校20个班的作品进行评比．在第一批评比中，随机抽取A、B、C、D四个班的征集作品，对其数量进行统计后，绘制如图两幅不完整的统计图．‎ ‎（1）第一批所抽取的4个班共征集到作品　 　件；在扇形统计图中表示C班的扇形的圆心角的度数为　 　；‎ ‎（2）补全条形统计图；‎ ‎（3）第一批评比中，A班D班各有一件、B班C班各有两件作品获得一等奖．现要在获得一等奖的作品中随机抽取两件在全校展出，用树状图或列表法求抽取的作品来自两个不同班级的概率．‎ ‎22．（8分）如图，AB是半圆AOB的直径，C是半圆上的一点，AD平分∠BAC交半圆于点D，过点D作DH⊥AC与AC的延长线交于点H．‎ ‎（1）求证：DH是半圆的切线；‎ ‎（2）若DH＝2‎5‎，sin∠BAC‎=‎‎5‎‎3‎，求半圆的直径．‎ 四、填空题（本大题共2小题，每小题5分，共10分）‎ ‎23．（5分）若不等式组‎2x＜3(x-3)+1‎‎3x+2‎‎4‎‎＞x+a恰有四个整数解，则a的取值范围是　 　．‎ ‎24．（5分）如图，矩形ABCD中，AD＝12，AB＝8，E是AB上一点，且EB＝3，F是BC上一动点，若将△EBF沿EF对折后，点B落在点P处，则点P到点D的最短距离为　 　．‎ 第23页（共23页）‎ 五、解答题（本大题共4小题，共40分）解答应写出文字说明、证明过程或演算步骤．‎ ‎25．（8分）如图，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P、点Q以相同的速度，同时从点A、点B出发．‎ ‎（1）如图1，连接AQ、CP．求证：△ABQ≌△CAP；‎ ‎（2）如图1，当点P、Q分别在AB、BC边上运动时，AQ、CP相交于点M，∠QMC的大小是否变化？若变化，请说明理由；若不变，求出它的度数；‎ ‎（3）如图2，当点P、Q在AB、BC的延长线上运动时，直线AQ、CP相交于M，∠QMC的大小是否变化？若变化，请说明理由；若不变，求出它的度数．‎ ‎26．（10分）如图，已知直线l：y＝﹣x+5．‎ ‎（1）当反比例函数y‎=‎kx（k＞0，x＞0）的图象与直线l在第一象限内至少有一个交点时，求k的取值范围．‎ ‎（2）若反比例函数y‎=‎kx（k＞0，x＞0）的图象与直线l在第一象限内相交于点A（x1，y1）、B（x2，y2），当x2﹣x1＝3时，求k的值，并根据图象写出此时关于x的不等式﹣x+5‎＜‎kx的解集．‎ 第23页（共23页）‎ ‎27．（10分）如图，⊙O的半径为R，其内接锐角三角形ABC中，∠A、∠B、∠C所对的边分别是a、b、c．‎ ‎（1）求证：asin∠A‎=bsin∠B=csin∠C=‎2R；‎ ‎（2）若∠A＝60°，∠C＝45°，BC＝4‎3‎，利用（1）的结论求AB的长和sin∠B的值．‎ ‎28．（12分）如图，二次函数y＝ax2+bx+x的图象过O（0，0）、A（1，0）、B（‎3‎‎2‎，‎3‎‎2‎）三点．‎ ‎（1）求二次函数的解析式；‎ ‎（2）若线段OB的垂直平分线与y轴交于点C，与二次函数的图象在x轴上方的部分相交于点D，求直线CD的解析式；‎ ‎（3）在直线CD下方的二次函数的图象上有一动点P，过点P作PQ⊥x轴，交直线CD于Q，当线段PQ的长最大时，求点P的坐标．‎ 第23页（共23页）‎ ‎2020年四川省凉山州中考数学试卷 参考答案与试题解析 一、选择题（本大题共12小题，每小题4分，共48分）在每小题给出的四个选项中只有一项是正确的，把正确选项的字母填涂在答题卡上相应的位置．‎ ‎1．（4分）﹣12020＝（　　）‎ A．1 B．﹣1 C．2020 D．﹣2020‎ ‎【解答】解：﹣12020＝﹣1．‎ 故选：B．‎ ‎2．（4分）如图，下列几何体的左视图不是矩形的是（　　）‎ A． B． C． D．‎ ‎【解答】解：A、圆柱的左视图是矩形，故本选项不符合题意；‎ B、三棱锥的左视图是三角形，故本选项符合题意；‎ C、三棱柱的左视图是矩形，故本选项不符合题意；‎ D、正方体的左视图是正方形，故本选项不符合题意．‎ 故选：B．‎ ‎3．（4分）点P （2，3）关于x轴对称的点P'的坐标是（　　）‎ A．（2，﹣3） B．（﹣2，3） C．（﹣2，﹣3） D．（3，2）‎ ‎【解答】解：点P（2，3）关于x轴对称的点P'的坐标是（2，﹣3）．‎ 故选：A．‎ ‎4．（4分）已知一组数据1，0，3，﹣1，x，2，3的平均数是1，则这组数据的众数是（　　）‎ A．﹣1 B．3 C．﹣1和3 D．1和3‎ ‎【解答】解：∵数据1，0，3，﹣1，x，2，3的平均数是1，‎ ‎∴1+0+3﹣1+x+2+3＝7×1，‎ 解得x＝﹣1，‎ 则这组数据为1，0，3，﹣1，﹣1，2，3，‎ ‎∴这组数据的众数为﹣1和3，‎ 故选：C．‎ 第23页（共23页）‎ ‎5．（4分）一元二次方程x2＝2x的根为（　　）‎ A．x＝0 B．x＝2 C．x＝0或x＝2 D．x＝0或x＝﹣2‎ ‎【解答】解：∵x2＝2x，‎ ‎∴x2﹣2x＝0，‎ 则x（x﹣2）＝0，‎ ‎∴x＝0或x﹣2＝0，‎ 解得x1＝0，x2＝2，‎ 故选：C．‎ ‎6．（4分）下列等式成立的是（　　）‎ A．‎81‎‎=‎±9 B．|‎5‎‎-‎2|‎=-‎5‎+‎2 ‎ C．（‎-‎‎1‎‎2‎）﹣1＝﹣2 D．（tan45°﹣1）0＝1‎ ‎【解答】解：A．‎81‎‎=‎9，此选项计算错误；‎ B．|‎5‎‎-‎2|‎=‎5‎-‎2，此选项错误；‎ C．（‎-‎‎1‎‎2‎）﹣1＝﹣2，此选项正确；‎ D．（tan45°﹣1）0无意义，此选项错误；‎ 故选：C．‎ ‎7．（4分）若一次函数y＝（2m+1）x+m﹣3的图象不经过第二象限，则m的取值范围是（　　）‎ A．m‎＞-‎‎1‎‎2‎ B．m＜3 C．‎-‎1‎‎2‎＜‎m＜3 D．‎-‎1‎‎2‎＜‎m≤3‎ ‎【解答】解：根据题意得‎2m+1＞0‎m-3≤0‎，‎ 解得‎-‎1‎‎2‎＜‎m≤3．‎ 故选：D．‎ ‎8．（4分）点C是线段AB的中点，点D是线段AC的三等分点．若线段AB＝12cm，则线段BD的长为（　　）‎ A．10cm B．8cm C．10cm 或8cm D．2cm 或4cm ‎【解答】解：∵C是线段AB的中点，AB＝12cm，‎ ‎∴AC＝BC‎=‎‎1‎‎2‎AB‎=‎1‎‎2‎×‎12＝6（cm），‎ 点D是线段AC的三等分点，‎ 第23页（共23页）‎ ‎①当AD‎=‎‎1‎‎3‎AC时，如图，‎ BD＝BC+CD＝BC‎+‎‎2‎‎3‎AC＝6+4＝10（cm）；‎ ‎②当AD‎=‎‎2‎‎3‎AC时，如图，‎ BD＝BC+CD′＝BC‎+‎‎1‎‎3‎AC＝6+2＝8（cm）．‎ 所以线段BD的长为10cm或8cm，‎ 故选：C．‎ ‎9．（4分）下列命题是真命题的是（　　）‎ A．顶点在圆上的角叫圆周角 ‎ B．三点确定一个圆 ‎ C．圆的切线垂直于半径 ‎ D．三角形的内心到三角形三边的距离相等 ‎【解答】解：A、顶点在圆上且两边都与圆相交的角叫圆周角，原命题是假命题；‎ B、不在同一直线上的三点确定一个圆，原命题是假命题；‎ C、圆的切线垂直于过切点的半径，原命题是假命题；‎ D、三角形的内心到三角形三边的距离相等，是真命题；‎ 故选：D．‎ ‎10．（4分）如图所示，△ABC的顶点在正方形网格的格点上，则tanA的值为（　　）‎ A．‎1‎‎2‎ B．‎2‎‎2‎ C．2 D．2‎‎2‎ ‎【解答】解：如图，连接BD，由网格的特点可得，BD⊥AC，‎ AD‎=‎2‎‎2‎‎+‎‎2‎‎2‎=‎2‎2‎，BD‎=‎1‎‎2‎‎+‎‎1‎‎2‎=‎‎2‎，‎ ‎∴tanA‎=BDAD=‎2‎‎2‎‎2‎=‎‎1‎‎2‎，‎ 故选：A．‎ 第23页（共23页）‎ ‎11．（4分）如图，等边三角形ABC和正方形ADEF都内接于⊙O，则AD：AB＝（　　）‎ A．2‎2‎：‎3‎ B．‎2‎：‎3‎ C．‎3‎：‎2‎ D．‎3‎：2‎‎2‎ ‎【解答】解：连接OA、OB、OD，过O作OH⊥AB于H，如图所示：‎ 则AH＝BH‎=‎‎1‎‎2‎AB，‎ ‎∵正方形ABCD和等边三角形AEF都内接于⊙O，‎ ‎∴∠AOB＝120°，∠AOD＝90°，‎ ‎∵OA＝OD＝OB，‎ ‎∴△AOD是等腰直角三角形，∠AOH＝∠BOH‎=‎1‎‎2‎×‎120°＝60°，‎ ‎∴AD‎=‎‎2‎OA，AH＝OA•sin60°‎=‎‎3‎‎2‎OA，‎ ‎∴AB＝2AH＝2‎×‎‎3‎‎2‎OA‎=‎‎3‎OA，‎ ‎∴ADAB‎=‎2‎OA‎3‎OA=‎‎2‎‎3‎，‎ 故选：B．‎ ‎12．（4分）二次函数y＝ax2+bx+c的图象如图所示，有如下结论：‎ ‎①abc＞0；‎ 第23页（共23页）‎ ‎②2a+b＝0；‎ ‎③3b﹣2c＜0；‎ ‎④am2+bm≥a+b（m为实数）．‎ 其中正确结论的个数是（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎【解答】解：①∵对称轴在y轴右侧，‎ ‎∴a、b异号，‎ ‎∴ab＜0，‎ ‎∵c＜0‎ ‎∴abc＞0‎ 故①正确；‎ ‎②∵对称轴x‎=-b‎2a=‎1，‎ ‎∴2a+b＝0；‎ 故②正确；‎ ‎③∵2a+b＝0，‎ ‎∴a‎=-‎‎1‎‎2‎b，‎ ‎∵当x＝﹣1时，y＝a﹣b+c＞0，‎ ‎∴‎-‎‎1‎‎2‎b﹣b+c＞0‎ ‎∴3b﹣2c＜0‎ 故③正确；‎ ‎④根据图象知，当x＝1时，y有最小值；‎ 当m为实数时，有am2+bm+c≥a+b+c，‎ 所以am2+bm≥a+b（m为实数）．‎ 故④正确．‎ 第23页（共23页）‎ 本题正确的结论有：①②③④，4个；‎ 故选：D．‎ 二、填空题（本大题共5小题，每小题4分，共20分）‎ ‎13．（4分）函数y‎=‎x+1‎中，自变量x的取值范围是　x≥﹣1　．‎ ‎【解答】解：由题意得，x+1≥0，‎ 解得x≥﹣1．‎ 故答案为：x≥﹣1．‎ ‎14．（4分）因式分解：a3﹣ab2＝　a（a+b）（a﹣b）　．‎ ‎【解答】解：a3﹣ab2＝a（a2﹣b2）＝a（a+b）（a﹣b）．‎ ‎15．（4分）如图，▱ABCD的对角线AC、BD相交于点O，OE∥AB交AD于点E，若OA＝1，△AOE的周长等于5，则▱ABCD的周长等于　16　．‎ ‎【解答】解：∵四边形ABCD是平行四边形，‎ ‎∴AB＝CD，AD＝BC，OB＝OD，‎ ‎∵OE∥AB，‎ ‎∴OE是△ABD的中位线，‎ ‎∴AB＝2OE，AD＝2AE，‎ ‎∵△AOE的周长等于5，‎ ‎∴OA+AE+OE＝5，‎ ‎∴AE+OE＝5﹣OA＝5﹣1＝4，‎ ‎∴AB+AD＝2AE+2OE＝8，‎ ‎∴▱ABCD的周长＝2×（AB+AD）＝2×8＝16；‎ 故答案为：16．‎ ‎16．（4分）如图，点C、D分别是半圆AOB上的三等分点，若阴影部分的面积是‎3‎‎2‎π，则半圆的半径OA的长为　3　．‎ 第23页（共23页）‎ ‎【解答】解：连接OC、OD、CD．‎ ‎∵△COD和△CBD等底等高，‎ ‎∴S△COD＝S△BCD．‎ ‎∵点C，D为半圆的三等分点，‎ ‎∴∠COD＝180°÷3＝60°，‎ ‎∴阴影部分的面积＝S扇形COD，‎ ‎∵阴影部分的面积是‎3‎‎2‎π，‎ ‎∴‎60π⋅‎r‎2‎‎360‎‎=‎‎3‎‎2‎π，‎ ‎∴r＝3，‎ 故答案为3．‎ ‎17．（4分）如图，矩形OABC的面积为‎100‎‎3‎，对角线OB与双曲线y‎=‎kx（k＞0，x＞0）相交于点D，且OB：OD＝5：3，则k的值为　12　．‎ ‎【解答】解：设D的坐标是（3m，3n），则B的坐标是（5m，5n）．‎ ‎∵矩形OABC的面积为‎100‎‎3‎，‎ ‎∴5m•5n‎=‎‎100‎‎3‎，‎ ‎∴mn‎=‎‎4‎‎3‎．‎ 第23页（共23页）‎ 把D的坐标代入函数解析式得：3n‎=‎k‎3m，‎ ‎∴k＝9mn＝9‎×‎4‎‎3‎=‎12．‎ 故答案为12．‎ 三、解答题（本大题共5小题，共32分）解答应写出文字说明、证明过程或演算步骤．‎ ‎18．（5分）解方程：x‎-x-2‎‎2‎=‎1‎+‎‎2x-1‎‎3‎．‎ ‎【解答】解：去分母，得：6x﹣3（x﹣2）＝6+2（2x﹣1），‎ 去括号，得：6x﹣3x+6＝6+4x﹣2，‎ 移项，得：6x﹣3x﹣4x＝6﹣6﹣2，‎ 合并同类项，得：﹣x＝﹣2，‎ 系数化为1，得：x＝2．‎ ‎19．（5分）化简求值：（2x+3）（2x﹣3）﹣（x+2）2+4（x+3），其中x‎=‎‎2‎．‎ ‎【解答】解：原式＝4x2﹣9﹣（x2+4x+4）+4x+12‎ ‎＝4x2﹣9﹣x2﹣4x﹣4+4x+12‎ ‎＝3x2﹣1，‎ 当x‎=‎‎2‎时，‎ 原式＝3×（‎2‎）2﹣1‎ ‎＝3×2﹣1‎ ‎＝6﹣1‎ ‎＝5．‎ ‎20．（7分）如图，一块材料的形状是锐角三角形ABC，边BC＝120mm，高AD＝80mm，把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是多少？‎ ‎【解答】解：∵四边形EGFH为正方形，‎ ‎∴BC∥EF，‎ 第23页（共23页）‎ ‎∴△AEF∽△ABC；‎ 设正方形零件的边长为x mm，则KD＝EF＝x，AK＝80﹣x，‎ ‎∵EF∥BC，‎ ‎∴△AEF∽△ABC，‎ ‎∵AD⊥BC，‎ ‎∴EFBC‎=‎AKAD，‎ ‎∴x‎120‎‎=‎‎80-x‎80‎，‎ 解得：x＝48．‎ 答：正方形零件的边长为48mm．‎ ‎21．（7分）某校团委在“五•四”青年节举办了一次“我的中国梦”作文大赛，分三批对全校20个班的作品进行评比．在第一批评比中，随机抽取A、B、C、D四个班的征集作品，对其数量进行统计后，绘制如图两幅不完整的统计图．‎ ‎（1）第一批所抽取的4个班共征集到作品　24　件；在扇形统计图中表示C班的扇形的圆心角的度数为　150°　；‎ ‎（2）补全条形统计图；‎ ‎（3）第一批评比中，A班D班各有一件、B班C班各有两件作品获得一等奖．现要在获得一等奖的作品中随机抽取两件在全校展出，用树状图或列表法求抽取的作品来自两个不同班级的概率．‎ 第23页（共23页）‎ ‎【解答】解：（1）第一批所抽取的4个班共征集到作品6÷25%＝24（件），‎ 则C班级作品数为24﹣（4+6+4）＝10（件），‎ ‎∴在扇形统计图中表示C班的扇形的圆心角的度数为360°‎×‎10‎‎24‎=‎150°，‎ 故答案为：24、150°；‎ ‎（2）补全图形如下：‎ ‎（3）列表如下：‎ A B B C C D A BA BA CA CA DA B AB BB CB CB DB B AB BB CB CB DB C AC BC BC CC DC C AC BC BC CC DC D AD BD BD CD CD 由表可知，共有30种等可能结果，其中抽取的作品来自两个不同班级的有26种结果，‎ ‎∴抽取的作品来自两个不同班级的概率为‎26‎‎30‎‎=‎‎13‎‎15‎．‎ 第23页（共23页）‎ ‎22．（8分）如图，AB是半圆AOB的直径，C是半圆上的一点，AD平分∠BAC交半圆于点D，过点D作DH⊥AC与AC的延长线交于点H．‎ ‎（1）求证：DH是半圆的切线；‎ ‎（2）若DH＝2‎5‎，sin∠BAC‎=‎‎5‎‎3‎，求半圆的直径．‎ ‎【解答】（1）证明：连接OD，‎ ‎∵OA＝OD，‎ ‎∴∠DAO＝∠ADO，‎ ‎∵AD平分∠BAC，‎ ‎∴∠CAD＝∠OAD，‎ ‎∴∠CAD＝∠ADO，‎ ‎∴AH∥OD，‎ ‎∵DH⊥AC，‎ ‎∴OD⊥DH，‎ ‎∴DH是半圆的切线；‎ ‎（2）解：连接BC交OD于E，‎ ‎∵AB是半圆AOB的直径，‎ ‎∴∠ACB＝90°，‎ ‎∴四边形CEDH是矩形，‎ ‎∴CE＝DH＝2‎5‎，∠DEC＝90°，‎ ‎∴OD⊥BC，‎ ‎∴BC＝2CE＝4‎5‎，‎ ‎∵sin∠BAC‎=BCAB=‎‎5‎‎3‎，‎ ‎∴AB＝12，‎ 即半圆的直径为12．‎ 第23页（共23页）‎ 四、填空题（本大题共2小题，每小题5分，共10分）‎ ‎23．（5分）若不等式组‎2x＜3(x-3)+1‎‎3x+2‎‎4‎‎＞x+a恰有四个整数解，则a的取值范围是　‎-‎11‎‎4‎≤‎a‎＜-‎‎5‎‎2‎　．‎ ‎【解答】解：解不等式2x＜3（x﹣3）+1，得：x＞8，‎ 解不等式‎3x+2‎‎4‎‎＞‎x+a，得：x＜2﹣4a，‎ ‎∵不等式组有4个整数解，‎ ‎∴12＜2﹣4a≤13，‎ 解得：‎-‎11‎‎4‎≤‎a‎＜-‎‎5‎‎2‎，‎ 故答案为：‎-‎11‎‎4‎≤‎a‎＜-‎‎5‎‎2‎．‎ ‎24．（5分）如图，矩形ABCD中，AD＝12，AB＝8，E是AB上一点，且EB＝3，F是BC上一动点，若将△EBF沿EF对折后，点B落在点P处，则点P到点D的最短距离为　10　．‎ ‎【解答】解：如图，连接PD，DE，‎ ‎∵四边形ABCD是矩形，‎ ‎∴∠A＝90°，‎ ‎∵AB＝8，BE＝3，‎ ‎∴AE＝5，‎ 第23页（共23页）‎ ‎∵AD＝12，‎ ‎∴DE‎=‎5‎‎2‎‎+1‎‎2‎‎2‎=‎13，‎ 由折叠得：EB＝EP＝3，‎ ‎∵EP+DP≥ED，‎ ‎∴当E、P、D共线时，DP最小，‎ ‎∴DP＝DE﹣EP＝13﹣3＝10；‎ 故答案为：10．‎ 五、解答题（本大题共4小题，共40分）解答应写出文字说明、证明过程或演算步骤．‎ ‎25．（8分）如图，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P、点Q以相同的速度，同时从点A、点B出发．‎ ‎（1）如图1，连接AQ、CP．求证：△ABQ≌△CAP；‎ ‎（2）如图1，当点P、Q分别在AB、BC边上运动时，AQ、CP相交于点M，∠QMC的大小是否变化？若变化，请说明理由；若不变，求出它的度数；‎ ‎（3）如图2，当点P、Q在AB、BC的延长线上运动时，直线AQ、CP相交于M，∠QMC的大小是否变化？若变化，请说明理由；若不变，求出它的度数．‎ ‎【解答】解：（1）证明：如图1，∵△ABC是等边三角形 ‎∴∠ABQ＝∠CAP＝60°，AB＝CA，‎ 又∵点P、Q运动速度相同，‎ ‎∴AP＝BQ，‎ 在△ABQ与△CAP中，‎ AB=CA‎∠ABQ=∠CPAAP=BQ‎，‎ ‎∴△ABQ≌△CAP（SAS）；‎ 第23页（共23页）‎ ‎（2）点P、Q在AB、BC边上运动的过程中，∠QMC不变．‎ 理由：∵△ABQ≌△CAP，‎ ‎∴∠BAQ＝∠ACP，‎ ‎∵∠QMC是△ACM的外角，‎ ‎∴∠QMC＝∠ACP+∠MAC＝∠BAQ+∠MAC＝∠BAC ‎∵∠BAC＝60°，‎ ‎∴∠QMC＝60°；‎ ‎（3）如图2，点P、Q在运动到终点后继续在射线AB、BC上运动时，∠QMC不变 理由：同理可得，△ABQ≌△CAP，‎ ‎∴∠BAQ＝∠ACP，‎ ‎∵∠QMC是△APM的外角，‎ ‎∴∠QMC＝∠BAQ+∠APM，‎ ‎∴∠QMC＝∠ACP+∠APM＝180°﹣∠PAC＝180°﹣60°＝120°，‎ 即若点P、Q在运动到终点后继续在射线AB、BC上运动，∠QMC的度数为120°．‎ ‎26．（10分）如图，已知直线l：y＝﹣x+5．‎ ‎（1）当反比例函数y‎=‎kx（k＞0，x＞0）的图象与直线l 第23页（共23页）‎ 在第一象限内至少有一个交点时，求k的取值范围．‎ ‎（2）若反比例函数y‎=‎kx（k＞0，x＞0）的图象与直线l在第一象限内相交于点A（x1，y1）、B（x2，y2），当x2﹣x1＝3时，求k的值，并根据图象写出此时关于x的不等式﹣x+5‎＜‎kx的解集．‎ ‎【解答】解：（1）将直线l的表达式与反比例函数表达式联立并整理得：x2﹣5x+k＝0，‎ 由题意得：△＝25﹣4k≥0，解得：k‎≤‎‎25‎‎4‎，‎ 故k的取值范围0＜k‎≤‎‎25‎‎4‎；‎ ‎（2）设点A（m，﹣m+5），而x2﹣x1＝3，则点B（m+3，﹣m+2），‎ 点A、B都在反比例函数上，故m（﹣m+5）＝（m+3）（﹣m+2），解得：m＝1，‎ 故点A、B的坐标分别为（1，4）、（4，1）；‎ 将点A的坐标代入反比例函数表达式并解得：k＝4×1＝4，‎ 观察函数图象知，当﹣x+5‎＜‎kx时，0＜x＜1或x＞4．‎ ‎27．（10分）如图，⊙O的半径为R，其内接锐角三角形ABC中，∠A、∠B、∠C所对的边分别是a、b、c．‎ ‎（1）求证：asin∠A‎=bsin∠B=csin∠C=‎2R；‎ ‎（2）若∠A＝60°，∠C＝45°，BC＝4‎3‎，利用（1）的结论求AB的长和sin∠B的值．‎ ‎【解答】（1）证明：作直径BE，连接CE，如图所示：‎ 第23页（共23页）‎ 则∠BCE＝90°，∠E＝∠A，‎ ‎∴sinA＝sinE‎=BCBE=‎a‎2R，‎ ‎∴asinA‎=‎2R，‎ 同理：bsin∠B‎=‎2R，csin∠C‎=‎2R，‎ ‎∴asin∠A‎=bsin∠B=csin∠C=‎2R；‎ ‎（2）解：由（1）得：ABsinC‎=‎BCsinA，‎ 即ABsin45°‎‎=‎4‎‎3‎sin60°‎=‎2R，‎ ‎∴AB‎=‎4‎3‎×‎‎2‎‎2‎‎3‎‎2‎=‎4‎2‎，2R‎=‎4‎‎3‎‎3‎‎2‎=‎8，‎ 过B作BH⊥AC于H，‎ ‎∵∠AHB＝∠BHC＝90°，‎ ‎∴AH＝AB•cos60°＝4‎2‎‎×‎1‎‎2‎=‎2‎2‎，CH‎=‎‎2‎‎2‎BC＝2‎6‎，‎ ‎∴AC＝AH+CH＝2（‎2‎‎+‎‎6‎），‎ ‎∴sin∠B‎=AC‎2R=‎2(‎2‎+‎6‎)‎‎8‎=‎‎2‎‎+‎‎6‎‎4‎．‎ ‎28．（12分）如图，二次函数y＝ax2+bx+x的图象过O（0，0）、A（1，0）、B（‎3‎‎2‎，‎3‎‎2‎）三点．‎ ‎（1）求二次函数的解析式；‎ ‎（2）若线段OB的垂直平分线与y轴交于点C，与二次函数的图象在x轴上方的部分相交于点D，求直线CD的解析式；‎ ‎（3）在直线CD下方的二次函数的图象上有一动点P，过点P作PQ⊥x轴，交直线CD于Q，当线段PQ的长最大时，求点P的坐标．‎ 第23页（共23页）‎ ‎【解答】解：（1）将点O、A、B的坐标代入抛物线表达式得c=0‎a+b+c=0‎‎3‎‎2‎‎=‎9‎‎4‎a+‎3‎‎2‎b+c，解得a=-‎‎2‎‎3‎‎3‎b=-‎‎2‎‎3‎‎3‎c=0‎，‎ 故抛物线的表达式为：y‎=‎‎2‎‎3‎‎3‎x2‎-‎‎2‎‎3‎‎3‎x；‎ ‎（2）由点B的坐标知，直线BO的倾斜角为30°，则OB中垂线（CD）与x负半轴的夹角为60°，‎ 故设CD的表达式为：y‎=-‎‎3‎x+b，而OB中点的坐标为（‎3‎‎4‎，‎3‎‎4‎），‎ 将该点坐标代入CD表达式并解得：b‎=‎‎3‎，‎ 故直线CD的表达式为：y‎=-‎‎3‎x‎+‎‎3‎；‎ ‎（3）设点P（x，‎2‎‎3‎‎3‎x2‎-‎‎2‎‎3‎‎3‎x），则点Q（x，‎-‎‎3‎x‎+‎‎3‎），‎ 则PQ‎=-‎‎3‎x‎+‎3‎-‎（‎2‎‎3‎‎3‎x2‎-‎‎2‎‎3‎‎3‎x）‎=-‎‎2‎‎3‎‎3‎x2‎-‎‎3‎‎3‎x‎+‎‎3‎，‎ ‎∵‎-‎2‎‎3‎‎3‎＜‎0，故PQ有最大值，此时点P的坐标为（‎-‎‎1‎‎4‎，‎27‎‎3‎‎16‎）．‎ 第23页（共23页）‎