湖南省常德市中考数学试题及解析 20页

‎2017年湖南省常德市中考数学试卷(解析版)‎ 一、选择题（本大题共8小题，每小题3分，共24分）‎ ‎1．下列各数中无理数为（　　）‎ A． B．0 C． D．﹣1‎ ‎【考点】26：无理数．‎ ‎【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．‎ ‎【解答】解：A、是无理数，选项正确；‎ B、0是整数是有理数，选项错误；‎ C、是分数，是有理数，选项错误；‎ D、﹣1是整数，是有理数，选项错误．‎ 故选A．‎ ‎　‎ ‎2．若一个角为75°，则它的余角的度数为（　　）‎ A．285° B．105° C．75° D．15°‎ ‎【考点】IL：余角和补角．‎ ‎【分析】依据余角的定义列出算式进行计算即可．‎ ‎【解答】解：它的余角=90°﹣75°=15°，‎ 故选D．‎ ‎　‎ ‎3．一元二次方程3x2﹣4x+1=0的根的情况为（　　）‎ A．没有实数根 B．只有一个实数根 C．两个相等的实数根 D．两个不相等的实数根 ‎【考点】AA：根的判别式．‎ ‎【分析】先计算判别式的意义，然后根据判别式的意义判断根的情况．‎ ‎【解答】解：∵△=（﹣4）2﹣4×3×1=4＞0‎ ‎∴方程有两个不相等的实数根．‎ 故选D．‎ ‎　‎ ‎4．如图是根据我市某天七个整点时的气温绘制成的统计图，则这七个整点时气温的中位数和平均数分别是（　　）‎ A．30，28 B．26，26 C．31，30 D．26，22‎ ‎【考点】W4：中位数；W2：加权平均数．‎ ‎【分析】此题根据中位数，平均数的定义解答．‎ ‎【解答】解：由图可知，把7个数据从小到大排列为22，22，23，26，28，30，31，中位数是第4位数，第4位是26，所以中位数是26．‎ 平均数是（22×2+23+26+28+30+31）÷7=26，所以平均数是26．‎ 故选：B．‎ ‎　‎ ‎5．下列各式由左到右的变形中，属于分解因式的是（　　）‎ A．a（m+n）=am+an B．a2﹣b2﹣c2=（a﹣b）（a+b）﹣c2‎ C．10x2﹣5x=5x（2x﹣1） D．x2﹣16+6x=（x+4）（x﹣4）+6x ‎【考点】51：因式分解的意义．‎ ‎【分析】根据因式分解的意义即可判断．‎ ‎【解答】解：（A）该变形为去括号，故A不是因式分解；‎ ‎（B）该等式右边没有化为几个整式的乘积形式，故B不是因式分解；‎ ‎（D）该等式右边没有化为几个整式的乘积形式，故D不是因式分解；‎ 故选（C）‎ ‎　‎ ‎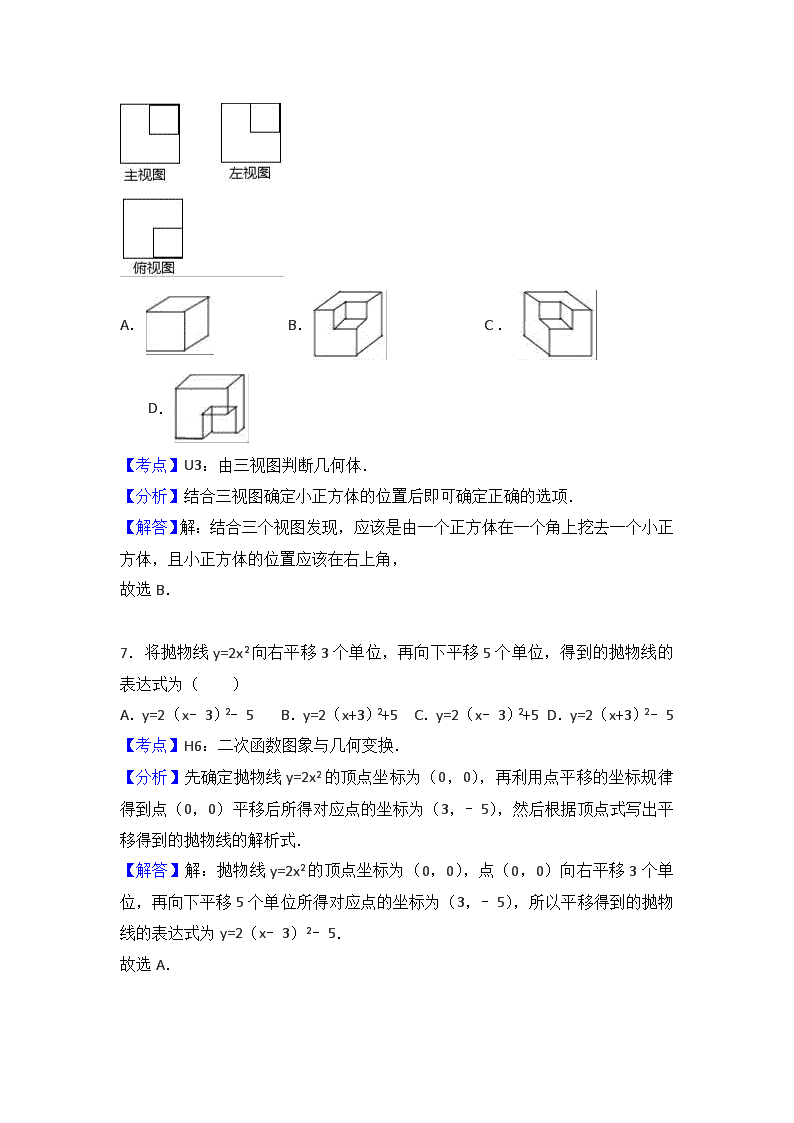6．如图是一个几何体的三视图，则这个几何体是（　　）‎ A． B． C． D．‎ ‎【考点】U3：由三视图判断几何体．‎ ‎【分析】结合三视图确定小正方体的位置后即可确定正确的选项．‎ ‎【解答】解：结合三个视图发现，应该是由一个正方体在一个角上挖去一个小正方体，且小正方体的位置应该在右上角，‎ 故选B．‎ ‎　‎ ‎7．将抛物线y=2x2向右平移3个单位，再向下平移5个单位，得到的抛物线的表达式为（　　）‎ A．y=2（x﹣3）2﹣5 B．y=2（x+3）2+5 C．y=2（x﹣3）2+5 D．y=2（x+3）2﹣5‎ ‎【考点】H6：二次函数图象与几何变换．‎ ‎【分析】先确定抛物线y=2x2的顶点坐标为（0，0），再利用点平移的坐标规律得到点（0，0）平移后所得对应点的坐标为（3，﹣5），然后根据顶点式写出平移得到的抛物线的解析式．‎ ‎【解答】解：抛物线y=2x2的顶点坐标为（0，0），点（0，0）向右平移3个单位，再向下平移5个单位所得对应点的坐标为（3，﹣5），所以平移得到的抛物线的表达式为y=2（x﹣3）2﹣5．‎ 故选A．‎ ‎　‎ ‎8．如表是一个4×4（4行4列共16个“数”组成）的奇妙方阵，从这个方阵中选四个“数”，而且这四个“数”中的任何两个不在同一行，也不在同一列，有很多选法，把每次选出的四个“数”相加，其和是定值，则方阵中第三行三列的“数”是（　　） ‎ ‎ 30‎ ‎ ‎ ‎ 2sin60°‎ ‎ 22‎ ‎﹣3‎ ‎﹣2‎ ‎﹣sin45°‎ ‎ 0‎ ‎|﹣5|‎ ‎ 6‎ ‎ ‎ ‎ 23‎ ‎ （）﹣1‎ ‎ 4‎ ‎ ‎ ‎ （）﹣1‎ A．5 B．6 C．7 D．8‎ ‎【考点】2C：实数的运算；6E：零指数幂；6F：负整数指数幂；T5：特殊角的三角函数值．‎ ‎【分析】分析可知第一行为1，2，3，4；第二行为﹣3，﹣2，﹣1，0；第三行为5，6，7，8，由此可得结果．‎ ‎【解答】解：∵第一行为1，2，3，4；第二行为﹣3，﹣2，﹣1，0；第四行为3，4，5，6‎ ‎∴第三行为5，6，7，8，‎ ‎∴方阵中第三行三列的“数”是7，‎ 故选C．‎ ‎　‎ 二、填空题（本小题共8小题，每小题3分，共24分）‎ ‎9．计算：|﹣2|﹣=　0　．‎ ‎【考点】2C：实数的运算．‎ ‎【分析】首先计算开方，然后计算减法，求出算式的值是多少即可．‎ ‎【解答】解：|﹣2|﹣‎ ‎=2﹣2‎ ‎=0‎ 故答案为：0．‎ ‎　‎ ‎10．分式方程+1=的解为　x=2　．‎ ‎【考点】B3：解分式方程．‎ ‎【分析】先把分式方程转化成整式方程，求出方程的解，再进行检验即可．‎ ‎【解答】解： +1=，‎ 方程两边都乘以x得：2+x=4，‎ 解得：x=2，‎ 检验：当x=2时，x≠0，‎ 即x=2是原方程的解，‎ 故答案为：x=2．‎ ‎　‎ ‎11．据统计：我国微信用户数量已突破887000000人，将887000000用科学记数法表示为　8.87×108　．‎ ‎【考点】1I：科学记数法—表示较大的数．‎ ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于10时，n是正数；当原数的绝对值小于1时，n是负数．‎ ‎【解答】解：887000000=8.87×108．‎ 故答案为：8.87×108．‎ ‎　‎ ‎12．命题：“如果m是整数，那么它是有理数”，则它的逆命题为：　“如果m是有理数，那么它是整数”　．‎ ‎【考点】O1：命题与定理．‎ ‎【分析】把一个命题的条件和结论互换就得到它的逆命题．‎ ‎【解答】解：命题：“如果m是整数，那么它是有理数”的逆命题为“如果m是有理数，那么它是整数”．‎ 故答案为“如果m是有理数，那么它是整数”．‎ ‎　‎ ‎13．彭山的枇杷大又甜，在今年5月18日“彭山枇杷节”期间，从山上5棵枇杷树上采摘到了200千克枇杷，请估计彭山近600棵枇杷树今年一共收获了枇杷　24000　千克．‎ ‎【考点】V5：用样本估计总体．‎ ‎【分析】先求出一棵枇杷树上采摘多少千克枇杷，再乘以彭山总的枇杷树的棵数，即可得出答案．‎ ‎【解答】解：根据题意得：‎ ‎200÷5×600=24000（千克），‎ 答：今年一共收获了枇杷24000千克；‎ 故答案为：24000．‎ ‎　‎ ‎14．如图，已知Rt△ABE中∠A=90°，∠B=60°，BE=10，D是线段AE上的一动点，过D作CD交BE于C，并使得∠CDE=30°，则CD长度的取值范围是　0≤CD≤5　．‎ ‎【考点】KO：含30度角的直角三角形；KP：直角三角形斜边上的中线．‎ ‎【分析】分点D与点E重合、点D与点A重合两种情况，根据等腰三角形的性质计算即可．‎ ‎【解答】解：当点D与点E重合时，CD=0，‎ 当点D与点A重合时，‎ ‎∵∠A=90°，∠B=60°，‎ ‎∴∠E=30°，‎ ‎∴∠CDE=∠E，∠CDB=∠B，‎ ‎∴CE=CD，CD=CB，‎ ‎∴CD=BE=5，‎ ‎∴0≤CD≤5，‎ 故答案为：0≤CD≤5．‎ ‎　‎ ‎15．如图，正方形EFGH的顶点在边长为2的正方形的边上．若设AE=x，正方形EFGH的面积为y，则y与x的函数关系为　y=2x2﹣4x+4　．‎ ‎【考点】HD：根据实际问题列二次函数关系式；LE：正方形的性质．‎ ‎【分析】由AAS证明△AHE≌△BEF，得出AE=BF=x，AH=BE=2﹣x，再根据勾股定理，求出EH2，即可得到y与x之间的函数关系式．‎ ‎【解答】解：如图所示：‎ ‎∵四边形ABCD是边长为1的正方形，‎ ‎∴∠A=∠B=90°，AB=2．‎ ‎∴∠1+∠2=90°，‎ ‎∵四边形EFGH为正方形，‎ ‎∴∠HEF=90°，EH=EF．‎ ‎∴∠1+∠3=90°，‎ ‎∴∠2=∠3，‎ 在△AHE与△BEF中，‎ ‎∵，‎ ‎∴△AHE≌△BEF（AAS），‎ ‎∴AE=BF=x，AH=BE=2﹣x，‎ 在Rt△AHE中，由勾股定理得：‎ EH2=AE2+AH2=x2+（2﹣x）2=2x2﹣4x+4；‎ 即y=2x2﹣4x+4（0＜x＜2），‎ 故答案为：y=2x2﹣4x+4．‎ ‎　‎ ‎16．如图，有一条折线A1B1A2B2A3B3A4B4…，它是由过A1（0，0），B1（2，2），A2（4，0）组成的折线依次平移4，8，12，…个单位得到的，直线y=kx+2与此折线恰有2n（n≥1，且为整数）个交点，则k的值为　﹣　．‎ ‎【考点】F8：一次函数图象上点的坐标特征；Q3：坐标与图形变化﹣平移．‎ ‎【分析】由点A1、A2的坐标，结合平移的距离即可得出点An的坐标，再由直线y=kx+2与此折线恰有2n（n≥1，且为整数）个交点，即可得出点An+1（4n，0）在直线y=kx+2上，依据依此函数图象上点的坐标特征，即可求出k值．‎ ‎【解答】解：∵A1（0，0），A2（4，0），A3（8，0），A4（12，0），…，‎ ‎∴An（4n﹣4，0）．‎ ‎∵直线y=kx+2与此折线恰有2n（n≥1，且为整数）个交点，‎ ‎∴点An+1（4n，0）在直线y=kx+2上，‎ ‎∴0=4nk+2，‎ 解得：k=﹣．‎ 故答案为：﹣．‎ ‎　‎ 三、解答题（本题共2小题，每小题5分，共10分．）‎ ‎17．甲、乙、丙三个同学站成一排进行毕业合影留念，请用列表法或树状图列出所有可能的情形，并求出甲、乙两人相邻的概率是多少？‎ ‎【考点】X6：列表法与树状图法．‎ ‎【分析】用树状图表示出所有情况，再根据概率公式求解可得．‎ ‎【解答】解：用树状图分析如下：‎ ‎∴一共有6种情况，甲、乙两人恰好相邻有4种情况，‎ ‎∴甲、乙两人相邻的概率是=．‎ ‎　‎ ‎18．求不等式组的整数解．‎ ‎【考点】CC：一元一次不等式组的整数解．‎ ‎【分析】先求出不等式的解，然后根据大大取大，小小取小，大小小大中间找，大大小小解不了，的口诀求出不等式组的解，进而求出整数解．‎ ‎【解答】解：解不等式①得x≤，‎ 解不等式②得x≥﹣，‎ ‎∴不等式组的解集为：﹣≤x≤‎ ‎∴不等式组的整数解是0，1，2．‎ ‎　‎ 四、解答题：本大题共2小题，每小题6分，共12分．‎ ‎19．先化简，再求值：（﹣）（﹣），其中x=4．‎ ‎【考点】6D：分式的化简求值．‎ ‎【分析】先根据分式的混合运算顺序和法则化简原式，再将x的值代入求解可得．‎ ‎【解答】解：原式=[+]•[﹣]‎ ‎=•（﹣）‎ ‎=•‎ ‎=x﹣2，‎ 当x=4时，‎ 原式=4﹣2=2．‎ ‎　‎ ‎20．在“一带一路”倡议下，我国已成为设施联通，贸易畅通的促进者，同时也带动了我国与沿线国家的货物交换的增速发展，如图是湘成物流园2016年通过“海、陆（汽车）、空、铁”四种模式运输货物的统计图．‎ 请根据统计图解决下面的问题：‎ ‎（1）该物流园2016年货运总量是多少万吨？‎ ‎（2）该物流园2016年空运货物的总量是多少万吨？并补全条形统计图；‎ ‎（3）求条形统计图中陆运货物量对应的扇形圆心角的度数？‎ ‎【考点】VC：条形统计图；VB：扇形统计图．‎ ‎【分析】（1）根据铁运的货运量以及百分比，即可得到物流园2016年货运总量；‎ ‎（2）根据空运的百分比，即可得到物流园2016年空运货物的总量，并据此补全条形统计图；‎ ‎（3）根据陆运的百分比乘上360°，即可得到陆运货物量对应的扇形圆心角的度数．‎ ‎【解答】解：（1）2016年货运总量是120÷50%=240吨；‎ ‎（2）2016年空运货物的总量是240×15%=36吨，‎ 条形统计图如下：‎ ‎（3）陆运货物量对应的扇形圆心角的度数为×360°=18°．‎ ‎　‎ 五、解答题：本大题共2小题，每小题7分，共14分．‎ ‎21．如图，已知反比例函数y=的图象经过点A（4，m），AB⊥x轴，且△AOB的面积为2．‎ ‎（1）求k和m的值；‎ ‎（2）若点C（x，y）也在反比例函数y=的图象上，当﹣3≤x≤‎ ‎﹣1时，求函数值y的取值范围．‎ ‎【考点】G5：反比例函数系数k的几何意义；G6：反比例函数图象上点的坐标特征．‎ ‎【分析】（1）根据反比例函数系数k的几何意义先得到k的值，然后把点A的坐标代入反比例函数解析式，可求出k的值；‎ ‎（2）先分别求出x=﹣3和﹣1时y的值，再根据反比例函数的性质求解．‎ ‎【解答】解：（1）∵△AOB的面积为2，‎ ‎∴k=4，‎ ‎∴反比例函数解析式为y=，‎ ‎∵A（4，m），‎ ‎∴m==1；‎ ‎（2）∵当x=﹣3时，y=﹣；‎ 当x=﹣1时，y=﹣4，‎ 又∵反比例函数y=在x＜0时，y随x的增大而减小，‎ ‎∴当﹣3≤x≤﹣1时，y的取值范围为﹣4≤y≤﹣．‎ ‎　‎ ‎22．如图，已知AB是⊙O的直径，CD与⊙O相切于C，BE∥CO．‎ ‎（1）求证：BC是∠ABE的平分线；‎ ‎（2）若DC=8，⊙O的半径OA=6，求CE的长．‎ ‎【考点】MC：切线的性质．‎ ‎【分析】（1）由BE∥CO，推出∠OCB=∠CBE，由OC=OB，推出∠OCB=∠OBC，可得∠CBE=∠CBO；‎ ‎（2）在Rt△CDO中，求出OD，由OC∥BE，可得=，由此即可解决问题；‎ ‎【解答】（1）证明：∵DE是切线，‎ ‎∴OC⊥DE，‎ ‎∵BE∥CO，‎ ‎∴∠OCB=∠CBE，‎ ‎∵OC=OB，‎ ‎∴∠OCB=∠OBC，‎ ‎∴∠CBE=∠CBO，‎ ‎∴BC平分∠ABE．‎ ‎（2）在Rt△CDO中，∵DC=8，OC=0A=6，‎ ‎∴OD==10，‎ ‎∵OC∥BE，‎ ‎∴=，‎ ‎∴=，‎ ‎∴EC=4.8．‎ ‎　‎ 六、解答题：本大题共2小题，每小题8分，共16分．‎ ‎23．收发微信红包已成为各类人群进行交流联系，增强感情的一部分，下面是甜甜和她的双胞胎妹妹在六一儿童节期间的对话．‎ 请问：（1）2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是多少？‎ ‎（2）2017年六一甜甜和她妹妹各收到了多少钱的微信红包？‎ ‎【考点】8A：一元一次方程的应用；AD：一元二次方程的应用．‎ ‎【分析】（1）一般用增长后的量=增长前的量×（1+增长率），2016年收到微信红包金额400（1+x）万元，在2016年的基础上再增长x，就是2017年收到微信红包金额400（1+x）（1+x），由此可列出方程400（1+x）2=484，求解即可．‎ ‎（2）设甜甜在2017年六一收到微信红包为y元，则她妹妹收到微信红包为（2y+34）元，根据她们共收到微信红包484元列出方程并解答．‎ ‎【解答】解：（1）设2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是x，‎ 依题意得：400（1+x）2=484，‎ 解得x1=0.1=10%，x2=﹣2.2（舍去）．‎ 答：2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是10%；‎ ‎（2）设甜甜在2017年六一收到微信红包为y元，‎ 依题意得：2y+34+y=484，‎ 解得y=150‎ 所以484﹣150=334（元）．‎ 答：甜甜在2017年六一收到微信红包为150元，则她妹妹收到微信红包为334元．‎ ‎　‎ ‎24．如图1，2分别是某款篮球架的实物图与示意图，已知底座BC=0.60米，底座BC与支架AC所成的角∠ACB=75°，支架AF的长为2.50米，篮板顶端F点到篮框D的距离FD=1.35米，篮板底部支架HE与支架AF所成的角∠FHE=60°，求篮框D到地面的距离（精确到0.01米）（参考数据：cos75°≈0.2588，sin75°≈0.9659，tan75°≈3.732，≈1.732，≈1.414）‎ ‎【考点】T8：解直角三角形的应用．‎ ‎【分析】延长FE交CB的延长线于M，过A作AG⊥FM于G，解直角三角形即可得到结论．‎ ‎【解答】解：延长FE交CB的延长线于M，过A作AG⊥FM于G，‎ 在Rt△ABC中，tan∠ACB=，‎ ‎∴AB=BC•tan75°=0.60×3.732=2.0292，‎ ‎∴GM=AB=2.0292，‎ 在Rt△AGF中，∵∠FAG=∠FHD=60°，sin∠FAG=，‎ ‎∴sin60°==，‎ ‎∴FG=4.33，‎ ‎∴DM=FG+GM﹣DF≈5.01米，‎ 答：篮框D到地面的距离是5.01米．‎ ‎　‎ 七、解答题：每小题10分，共20分。‎ ‎25．如图，已知抛物线的对称轴是y轴，且点（2，2），（1，）在抛物线上，点P是抛物线上不与顶点N重合的一动点，过P作PA⊥x轴于A，PC⊥y轴于C，延长PC交抛物线于E，设M是O关于抛物线顶点N的对称点，D是C点关于N的对称点．‎ ‎（1）求抛物线的解析式及顶点N的坐标；‎ ‎（2）求证：四边形PMDA是平行四边形；‎ ‎（3）求证：△DPE∽△PAM，并求出当它们的相似比为时的点P的坐标．‎ ‎【考点】HF：二次函数综合题．‎ ‎【分析】（1）由已知点的坐标，利用待定系数法可求得抛物线的解析式，可求得其顶点N的坐标；‎ ‎（2）设P点横坐标为t，则可表示出C、D、M、A的坐标，从而可表示出PA和DM的长，由PA=DM可证得结论；‎ ‎（3）设P点横坐标为t，在Rt△PCM中，可表示出PM，可求得PM=PA，可知四边形PMDA为菱形，由菱形的性质和抛物线的对称性可得∠PDE=∠APM，可证得结论，在Rt△AOM中，用t表示出AM的长，再表示出PE的长，由相似比为可得到关于t的方程，可求得t的值，可求得P点坐标．‎ ‎【解答】（1）解：∵抛物线的对称轴是y轴，‎ ‎∴可设抛物线解析式为y=ax2+c，‎ ‎∵点（2，2），（1，）在抛物线上，‎ ‎∴，解得，‎ ‎∴抛物线解析式为y=x2+1，‎ ‎∴N点坐标为（0，1）；‎ ‎（2）证明：设P（t， t2+1），则C（0， t2+1），PA=t2+1，‎ ‎∵M是O关于抛物线顶点N的对称点，D是C点关于N的对称点，且N（0，1），‎ ‎∴M（0，2），‎ ‎∵OC=t2+1，ON=1，‎ ‎∴DM=CN=t2+1﹣1=t2，‎ ‎∴OD=t2﹣1，‎ ‎∴D（0，﹣t2+1），‎ ‎∴DM=2﹣（﹣t2+1）=t2+1=PA，且PM∥DM，‎ ‎∴四边形PMDA为平行四边形；‎ ‎（3）解：同（2）设P（t， t2+1），则C（0， t2+1），PA=t2+1，PC=|t|，‎ ‎∵M（0，2），‎ ‎∴CM=t2+1﹣2=t2﹣1，‎ 在Rt△PMC中，由勾股定理可得PM====t2+1=PA，且四边形PMDA为平行四边形，‎ ‎∴四边形PMDA为菱形，‎ ‎∴∠APM=∠ADM=2∠PDM，‎ ‎∵PE⊥y轴，且抛物线对称轴为y轴，‎ ‎∴DP=DE，且∠PDE=2∠PDM，‎ ‎∴∠PDE=∠APM，且=，‎ ‎∴△DPE∽△PAM；‎ ‎∵OA=|t|，OM=2，‎ ‎∴AM=，且PE=2PC=2|t|，‎ 当相似比为时，则=，即=，解得t=2或t=﹣2，‎ ‎∴P点坐标为（2，4）或（﹣2，4）．‎ ‎　‎ ‎26．如图，直角△ABC中，∠BAC=90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F．‎ ‎（1）如图1，若BD=BA，求证：△ABE≌△DBE；‎ ‎（2）如图2，若BD=4DC，取AB的中点G，连接CG交AD于M，求证：①GM=2MC；②AG2=AF•AC．‎ ‎【考点】S9：相似三角形的判定与性质；KD：全等三角形的判定与性质．‎ ‎【分析】（1）根据全等三角形的判定定理即可得到结论；‎ ‎（2）①过G作GH∥AD交BC于H，由AG=BG，得到BH=DH，根据已知条件设DC=1，BD=4，得到BH=DH=2，根据平行线分线段成比例定理得到==，求得GM=2MC；‎ ‎②过C作CN⊥AD交AD的延长线于N，则CN∥AG，根据相似三角形的性质得到=，由①知GM=2MC，得到2NC=AG，根据相似三角形的性质得到=，等量代换得到=，于是得到结论．‎ ‎【解答】证明：（1）在Rt△ABE和Rt△DBE中，，‎ ‎∴△ABE≌△DBE；‎ ‎（2）①过G作GH∥AD交BC于H，‎ ‎∵AG=BG，‎ ‎∴BH=DH，‎ ‎∵BD=4DC，‎ 设DC=1，BD=4，‎ ‎∴BH=DH=2，‎ ‎∵GH∥AD，‎ ‎∴==，‎ ‎∴GM=2MC；‎ ‎②过C作CN⊥AC交AD的延长线于N，则CN∥AG，‎ ‎∴△AGM∽△NCM，‎ ‎∴=，‎ 由①知GM=2MC，‎ ‎∴2NC=AG，‎ ‎∵∠BAC=∠AEB=90°，‎ ‎∴∠ABF=∠CAN=90°﹣∠BAE，‎ ‎∴△ACN∽△BAF，‎ ‎∴=，‎ ‎∵AB=AG，‎ ‎∴=，‎ ‎∴2CN•AG=AF•AC，‎ ‎∴AG2=AF•AC．‎ ‎　‎