安徽省优质名校中考数学考前强化试题及答案圆 10页

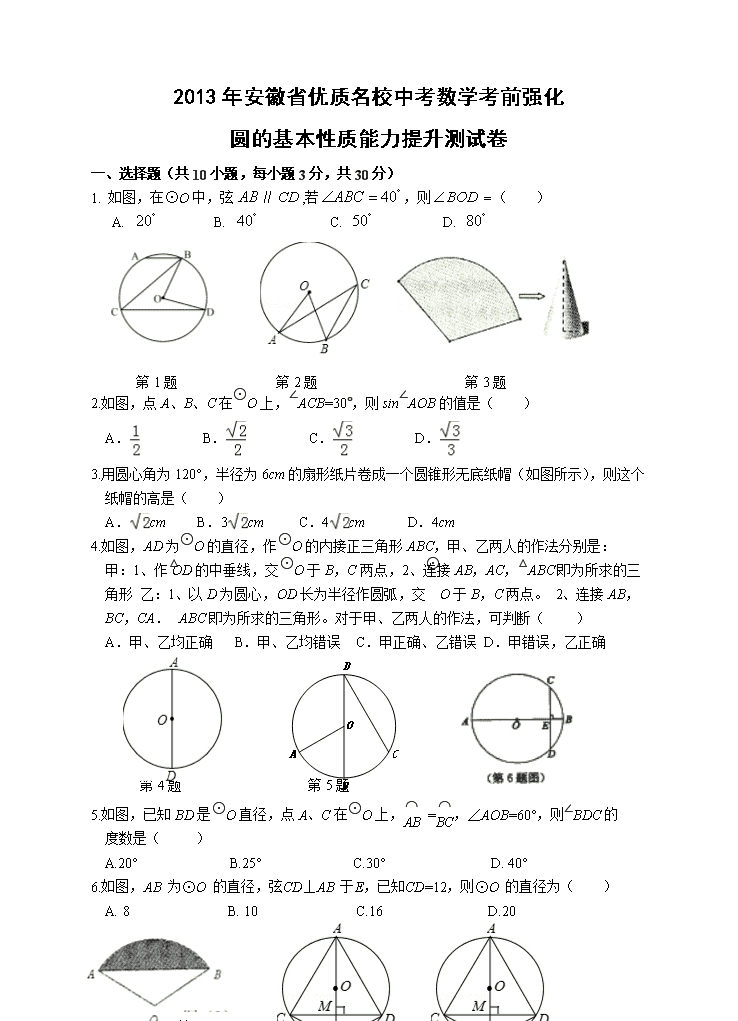
‎2013年安徽省优质名校中考数学考前强化 圆的基本性质能力提升测试卷 一、选择题（共10小题，每小题3分，共30分）‎ ‎1. 如图，在⊙O中，弦∥,若，则（ ）‎ A. B. C. D. ‎ 第1题 第2题 第3题 ‎ ‎2.如图，点A、B、C在⊙O上，∠ACB=30°，则sin∠AOB的值是（ 　） A．　　 B．　　 C．　 　D．‎ ‎3.用圆心角为120°，半径为6cm的扇形纸片卷成一个圆锥形无底纸帽（如图所示），则这个纸帽的高是（　　）‎ A．cm　 　B．3cm　 C．4cm　　 D．4cm ‎4.如图，AD为⊙O的直径，作⊙O的内接正三角形ABC，甲、乙两人的作法分别是：‎ 甲：1、作OD的中垂线，交⊙O于B，C两点，2、连接AB，AC，△ABC即为所求的三角形 乙：1、以D为圆心，OD长为半径作圆弧，交⊙O于B，C两点。 2、连接AB，BC，CA．△ABC即为所求的三角形。对于甲、乙两人的作法，可判断（　 　）‎ A．甲、乙均正确 B．甲、乙均错误 C．甲正确、乙错误 D．甲错误，乙正确 ‎ 第4题 第5题 ‎ ‎5.如图，已知BD是⊙O直径，点A、C在⊙O上， =，∠AOB=60°，则∠BDC的 度数是（ ）‎ A.20° B.25° C.30° D. 40°‎ ‎6.如图，AB 为⊙O 的直径，弦CD⊥AB 于E，已知CD=12，则⊙O 的直径为（ ）‎ 第9题 第8题 A. 8 B. 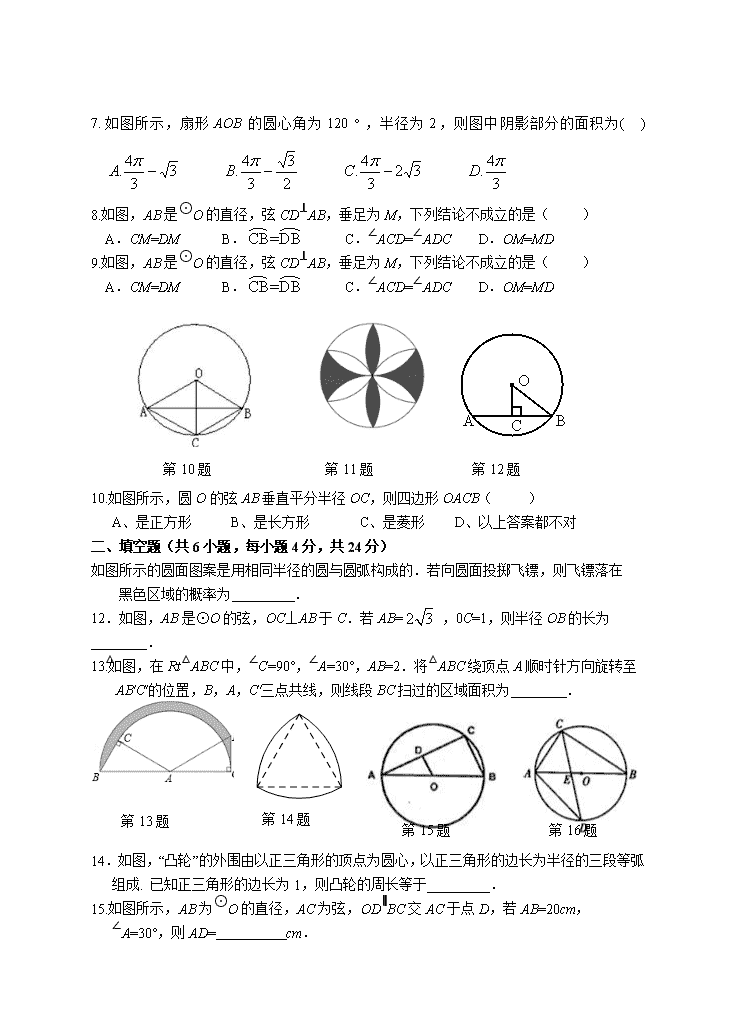10 C.16 D.20‎ 第7题 ‎7.如图所示，扇形AOB的圆心角为120︒，半径为2，则图中阴影部分的面积为( ) ‎ ‎8.如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是（　 　）‎ A．CM=DM　　 B．　　 C．∠ACD=∠ADC　　D．OM=MD ‎9.如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是（　 　）‎ A．CM=DM　 　B．　　 C．∠ACD=∠ADC　　D．OM=MD 第12题 第11题 第10题 ‎10.如图所示，圆O的弦AB垂直平分半径OC，则四边形OACB（ 　　）‎ A、是正方形 B、是长方形 C、是菱形 D、以上答案都不对 二、填空题（共6小题，每小题4分，共24分）‎ 如图所示的圆面图案是用相同半径的圆与圆弧构成的．若向圆面投掷飞镖，则飞镖落在 ‎ 黑色区域的概率为　 　．‎ ‎12．如图，AB是⊙O的弦，OC⊥AB于C．若AB= ，0C=1，则半径OB的长为________．‎ ‎13.如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=2．将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置，B，A，C′三点共线，则线段BC扫过的区域面积为　 　．‎ 第13题 第14题 第16题 第15题 ‎14．如图，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成. 已知正三角形的边长为1，则凸轮的周长等于_________．‎ ‎15.如图所示，AB为⊙O的直径，AC为弦，OD∥BC交AC于点D，若AB=20cm，‎ ‎∠A=30°，则AD=　 　cm．‎ ‎16.如图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交AB于E，交⊙O于D．则AD=_____________．‎ 三、解答题（共7题，共66分）‎ ‎17、（本题8分）如图所示,已知F是以O为圆心,BC为直径的半圆上任一点,A是弧BF的 ‎.‎ O D C F B A 中点,AD⊥BC于点D.求证:AD=BF.‎ ‎18（本题8分）.如图,⊙O的直径AB和弦CD相交于点E,已知AE=6cm,EB=2cm,‎ ‎∠CEA=30°, 求CD的长. ‎ ‎19．（本题8分）如图所示,OA、OB、OC都是圆O的半径,∠AOB=2∠BOC． 求证:∠ACB=2∠BAC.‎ ‎20、（本题10分）如图，弧AC是劣弧，M是弧AC中点，B为弧AC上任意一点，自M向BC弦引垂线，垂足为D，求证：AB+BD=DC。‎ A O B C D E ‎21、(本题10分）.如图所示，AB＝AC，AB为⊙O的直径，AC、BC分别交⊙O于E、D，连结ED、BE．‎ ‎(1) 试判断DE与BD是否相等，并说明理由；‎ ‎(2) 如果BC＝6，AB＝5，求BE的长．‎ ‎22．如图，在半径为2的扇形中，∠，点是弧上的一个动点（不与点、重合）⊥，⊥，垂足分别为、．‎ ‎（1）当时，求线段的长；‎ ‎（2）在△中是否存在长度保持不变的边？如果存在，请指出并求其长度，如果不存在，请说明理由；‎ ‎（3）设，△的面积为，求关于的函数关系式，并写出自变量取值范围．‎ ‎23.（本题12分）如图，半径为2的⊙C与x轴的正半轴交于点A，与y轴的正半轴交于点B，点C的坐标为（1，0）．若抛物线过A、B两点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在抛物线上是否存在点P，使得∠PBO=∠POB？若存在，求出点P的坐标；若不存在说明理由；‎ ‎（3）若点M是抛物线（在第一象限内的部分）上一点，△MAB的面积为S，求S的最大（小）值．‎ 参考答案 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 D C C A C D A D D C 二、填空题 ‎11. 12，2 13. 14. 15. 16. ‎ 三、解答题 ‎17（本题8分）如图所示,已知F是以O为圆心,BC为直径的半圆上任一点,A是弧BF的 A F B D C E O 中点,AD⊥BC于点D.求证:AD=BF.‎ ‎18（本题8分）.如图,⊙O的直径AB和弦CD相交于点E,已知AE=6cm,EB=2cm,‎ H ‎∠CEA=30°, 求CD的长. ‎ ‎19．（本题8分）如图所示,OA、OB、OC都是圆O的半径,∠AOB=2∠BOC．‎ 求证:∠ACB=2∠BAC.‎ ‎20（本题10分）如图，弧AC是劣弧，M是弧AC中点，B为弧AC上任意一点，自M向BC弦引垂线，垂足为D，求证：AB+BD=DC。‎ H ‎21.如图所示，AB＝AC，AB为⊙O的直径，AC、BC分别交⊙O于E、D，连结ED、BE．‎ ‎(1) 试判断DE与BD是否相等，并说明理由；‎ A O B C D E ‎(2) 如果BC＝6，AB＝5，求BE的长．‎ 解：(1) 连结AD. ∵AB是⊙O的直径，∴AD⊥BC，BE⊥AC.‎ ‎∵AB=AC，∴BD=CD，∴DE=BD.‎ ‎(2) 由勾股定理，得BC2-CE2=BE2=AB2-AE2.‎ 设AE=x，则62-(5-x)2=52-x2，解得x=.‎ ‎∴BE=.‎ ‎22.解 ‎23.解：（1）如答图1，连接OB．‎ ‎∵BC=2，OC=1 ∴OB= ∴B（0，）‎ 将A（3，0），B（0，）代入二次函数的表达式 得 ，解得： ，‎ ‎∴．‎ ‎（2）存在．‎ 如答图2，作线段OB的垂直平分线l，与抛物线的交点即为点P．‎ ‎∵B（0，），O（0，0）， ∴直线l的表达式为．代入抛物线的表达式，‎ 得； 解得，‎ ‎∴P（）．‎ ‎（3）如答图3，作MH⊥x轴于点H．‎ 设M（ ），‎ 则S△MAB=S梯形MBOH+S△MHA﹣S△OAB=（MH+OB）•OH+HA•MH﹣OA•OB ‎=‎ ‎= ∵，‎ ‎∴ ‎ ‎= ‎ ‎∴当时，取得最大值，最大值为．‎