2019年江苏省盐城市中考数学试卷 27页

第 1页（共 27页） 2019 年江苏省盐城市中考数学试卷 一、选择题（本大题共有 8 小题，每小题 3 分，共 24 分，在每小题所给出的四个选项只有 一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置） 1．（3 分）如图，数轴上点 A 表示的数是（ ） A．﹣1 B．0 C．1 D．2 2．（3 分）下列图形中，既是轴对称图形又是中心对称图形的是（ ） A． B． C． D． 3．（3 分）若 有意义，则 x 的取值范围是（ ） A．x≥2 B．x≥﹣2 C．x＞2 D．x＞﹣2 4．（3 分）如图，点 D、E 分别是△ABC 边 BA、BC 的中点，AC＝3，则 DE 的长为（ ） A．2 B． C．3 D． 5．（3 分）如图是由 6 个小正方体搭成的物体，该所示物体的主视图是（ ） A． B． C． D． 6．（3 分）下列运算正确的是（ ） A．a5•a2＝a10 B．a3÷a＝a2 C．2a+a＝2a2 D．（a2）3＝a5 7．（3 分）正在建设中的北京大兴国际机场规划建设面积约 1400000 平方米的航站楼，数据 第 2页（共 27页） 1400000 用科学记数法应表示为（ ） A．0.14×108 B．1.4×107 C．1.4×106 D．14×105 8．（3 分）关于 x 的一元二次方程 x2+kx﹣2＝0（k 为实数）根的情况是（ ） A．有两个不相等的实数根 B．有两个相等的实数根 C．没有实数根 D．不能确定 二、填空题（本大题共有 8 小题，每小题 3 分，共 24 分.不需写出解答过程，请将答案直接 写在答题卡的相应位置上） 9．（3 分）如图，直线 a∥b，∠1＝50°，那么∠2＝ °． 10．（3 分）分解因式：x2﹣1＝ ． 11．（3 分）如图，转盘中 6 个扇形的面积都相等．任意转动转盘 1 次，当转盘停止转动时， 指针落在阴影部分的概率为 ． 12．（3 分）甲、乙两人在 100 米短跑训练中，某 5 次的平均成绩相等，甲的方差是 0.14s2， 乙的方差是 0.06s2，这 5 次短跑训练成绩较稳定的是 ．（填“甲”或“乙”） 13．（3 分）设 x1、x2 是方程 x2﹣3x+2＝0 的两个根，则 x1+x2﹣x1•x2＝ ． 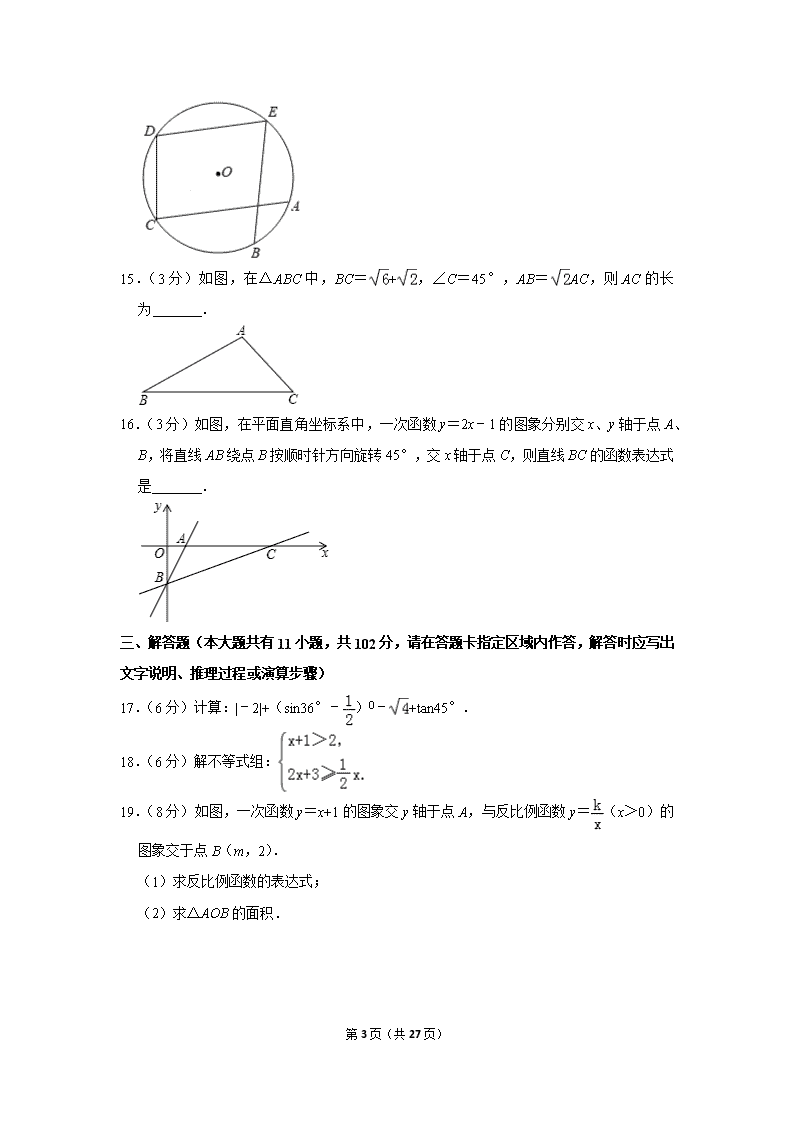14．（3 分）如图，点 A、B、C、D、E 在 ⊙ O 上，且 为 50°，则∠E+∠C＝ °． 第 3页（共 27页） 15．（3 分）如图，在△ABC 中，BC＝ + ，∠C＝45°，AB＝ AC，则 AC 的长为 ． 16．（3 分）如图，在平面直角坐标系中，一次函数 y＝2x﹣1 的图象分别交 x、y 轴于点 A、 B，将直线 AB 绕点 B 按顺时针方向旋转 45°，交 x 轴于点 C，则直线 BC 的函数表达式 是 ． 三、解答题（本大题共有 11 小题，共 102 分，请在答题卡指定区域内作答，解答时应写出 文字说明、推理过程或演算步骤） 17．（6 分）计算：|﹣2|+（sin36°﹣ ）0﹣ +tan45°． 18．（6 分）解不等式组： 19．（8 分）如图，一次函数 y＝x+1 的图象交 y 轴于点 A，与反比例函数 y＝ （x＞0）的 图象交于点 B（m，2）． （1）求反比例函数的表达式； （2）求△AOB 的面积． 20．（8 分）在一个不透明的布袋中，有 2 个红球，1 个白球，这些球除颜色外都相同． （1）搅匀后从中任意摸出 1 个球，摸到红球的概率是 ． （2）搅匀后先从中任意摸出 1 个球（不放回），再从余下的球中任意摸出 1 个球．求两 次都摸到红球的概率．（用树状图或表格列出所有等可能出现的结果） 21．（8 分）如图，AD 是△ABC 的角平分线． 第 4页（共 27页） （1）作线段 AD 的垂直平分线 EF，分别交 AB、AC 于点 E、F；（用直尺和圆规作图， 标明字母，保留作图痕迹，不写作法．） （2）连接 DE、DF，四边形 AEDF 是 形．（直接写出答案） 22．（10 分）体育器材室有 A、B 两种型号的实心球，1 只 A 型球与 1 只 B 型球的质量共 7 千克，3 只 A 型球与 1 只 B 型球的质量共 13 千克． （1）每只 A 型球、B 型球的质量分别是多少千克？ （2）现有 A 型球、B 型球的质量共 17 千克，则 A 型球、B 型球各有多少只？ 23．（10 分）某公司共有 400 名销售人员，为了解该公司销售人员某季度商品销售情况，随 机抽取部分销售人员该季度的销售数量，并把所得数据整理后绘制成如下统计图表进行 分析． 频数分布表 组别 销售数量（件） 频数 频率 A 20≤x＜40 3 0.06 B 40≤x＜60 7 0.14 C 60≤x＜80 13 a D 80≤x＜100 m 0.46 E 100≤x＜120 4 0.08 合计 b 1 请根据以上信息，解决下列问题： （1）频数分布表中，a＝ 、b＝ ； （2）补全频数分布直方图； （3）如果该季度销量不低于 80 件的销售人员将被评为“优秀员工”，试估计该季度被评 为“优秀员工”的人数． 第 5页（共 27页） 24．（10 分）如图，在 Rt△ABC 中，∠ACB＝90°，CD 是斜边 AB 上的中线，以 CD 为直 径的 ⊙ O 分别交 AC、BC 于点 M、N，过点 N 作 NE⊥AB，垂足为 E． （1）若 ⊙ O 的半径为 ，AC＝6，求 BN 的长； （2）求证：NE 与 ⊙ O 相切． 25．（10 分）如图 ① 是一张矩形纸片，按以下步骤进行操作： （Ⅰ）将矩形纸片沿 DF 折叠，使点 A 落在 CD 边上点 E 处，如图 ② ； （Ⅱ）在第一次折叠的基础上，过点 C 再次折叠，使得点 B 落在边 CD 上点 B′处，如 图 ③ ，两次折痕交于点 O； （Ⅲ）展开纸片，分别连接 OB、OE、OC、FD，如图 ④ ． 【探究】 （1）证明：△OBC≌△OED； （ 2 ） 若 AB ＝ 8 ， 设 BC 为 x ， OB2 为 y ， 求 y 关 于 x 的 关 系 式 ． 26．（12 分）【生活观察】甲、乙两人买菜，甲习惯买一定质量的菜，乙习惯买一定金额的 第 6页（共 27页） 菜，两人每次买菜的单价相同，例如： 第一次 菜价 3 元/千克 质量 金额 甲 1 千克 3 元 乙 1 千克 3 元 第二次： 菜价 2 元/千克 质量 金额 甲 1 千克 元 乙 千克 3 元 （1）完成上表； （2）计算甲两次买菜的均价和乙两次买菜的均价．（均价＝总金额÷总质量） 【数学思考】设甲每次买质量为 m 千克的菜，乙每次买金额为 n 元的菜，两次的单价分 别是 a 元/千克、b 元/千克，用含有 m、n、a、b 的式子，分别表示出甲、乙两次买菜的 均价 、 ，比较 、 的大小，并说明理由． 【知识迁移】某船在相距为 s 的甲、乙两码头间往返航行一次．在没有水流时，船的速 度为 v，所需时间为 t1；如果水流速度为 p 时（p＜v），船顺水航行速度为（v+p），逆水 航行速度为（v﹣p），所需时间为 t2．请借鉴上面的研究经验，比较 t1、t2 的大小，并说 明理由． 27．（14 分）如图所示，二次函数 y＝k（x﹣1）2+2 的图象与一次函数 y＝kx﹣k+2 的图象交 于 A、B 两点，点 B 在点 A 的右侧，直线 AB 分别与 x、y 轴交于 C、D 两点，其中 k＜0． （1）求 A、B 两点的横坐标； （2）若△OAB 是以 OA 为腰的等腰三角形，求 k 的值； （3）二次函数图象的对称轴与 x 轴交于点 E，是否存在实数 k，使得∠ODC＝2∠BEC， 若存在，求出 k 的值；若不存在，说明理由． 第 7页（共 27页） 第 8页（共 27页） 2019 年江苏省盐城市中考数学试卷 参考答案与试题解析 一、选择题（本大题共有 8 小题，每小题 3 分，共 24 分，在每小题所给出的四个选项只有 一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置） 1．（3 分）如图，数轴上点 A 表示的数是（ ） A．﹣1 B．0 C．1 D．2 【分析】根据数轴直接回答即可． 【解答】解：数轴上点 A 所表示的数是 1． 故选：C． 【点评】此题考查了数轴上的点和实数之间的对应关系． 2．（3 分）下列图形中，既是轴对称图形又是中心对称图形的是（ ） A． B． C． D． 【分析】直接利用轴对称图形和中心对称图形的概念求解． 【解答】解：A、是轴对称图形，不是中心对称图形，故此选项错误； B、既是中心对称图形也是轴对称图形，故此选项正确； C、不是轴对称图形，是中心对称图形，故此选项错误； D、不是轴对称图形，也不是中心对称图形，故此选项错误． 故选：B． 【点评】此题主要考查了中心对称与轴对称的概念：轴对称的关键是寻找对称轴，两边 图象折叠后可重合，中心对称是要寻找对称中心，旋转 180°后与原图重合． 3．（3 分）若 有意义，则 x 的取值范围是（ ） A．x≥2 B．x≥﹣2 C．x＞2 D．x＞﹣2 【分析】二次根式有意义，被开方数是非负数． 【解答】解：依题意，得 x﹣2≥0， 第 9页（共 27页） 解得，x≥2． 故选：A． 【点评】本题考查了二次根式有意义的条件．概念：式子 （a≥0）叫二次根式．性质： 二次根式中的被开方数必须是非负数，否则二次根式无意义． 4．（3 分）如图，点 D、E 分别是△ABC 边 BA、BC 的中点，AC＝3，则 DE 的长为（ ） A．2 B． C．3 D． 【分析】直接利用中位线的定义得出 DE 是△ABC 的中位线，进而利用中位线的性质得 出答案． 【解答】解：∵点 D、E 分别是△ABC 的边 BA、BC 的中点， ∴DE 是△ABC 的中位线， ∴DE＝ AC＝1.5． 故选：D． 【点评】此题主要考查了三角形中位线定理，正确得出 DE 是△ABC 的中位线是解题关 键． 5．（3 分）如图是由 6 个小正方体搭成的物体，该所示物体的主视图是（ ） A． B． C． D． 【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中． 【解答】解：从正面看易得第一层有 3 个正方形，第二层中间有一个正方形，如图所示： 故选：C． 第 10页（共 27页） 【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图． 6．（3 分）下列运算正确的是（ ） A．a5•a2＝a10 B．a3÷a＝a2 C．2a+a＝2a2 D．（a2）3＝a5 【分析】分别根据同底数幂相乘法则、同底数幂的除法法则、合并同类项的法则以及幂 的乘方法则化简即可． 【解答】解：A、a5•a2＝a7，故选项 A 不合题意； B、a3÷a＝a2，故选项 B 符合题意； C、2a+a＝3a，故选项 C 不合题意； D、（a2）3＝a6，故选项 D 不合题意． 故选：B． 【点评】本题主要考查了幂的运算性质以及合并同类项的法则，熟练掌握法则是解答本 题的关键． 7．（3 分）正在建设中的北京大兴国际机场规划建设面积约 1400000 平方米的航站楼，数据 1400000 用科学记数法应表示为（ ） A．0.14×108 B．1.4×107 C．1.4×106 D．14×105 【分析】利用科学记数法的表示形式进行解答即可 【解答】解： 科学记数法表示：1400 000＝1.4×106 故选：C． 【点评】本题主要考查科学记数法，科学记数法是指把一个数表示成 a×10 的 n 次幂的 形式（1≤a＜10，n 为正整数．） 8．（3 分）关于 x 的一元二次方程 x2+kx﹣2＝0（k 为实数）根的情况是（ ） A．有两个不相等的实数根 B．有两个相等的实数根 C．没有实数根 D．不能确定 【分析】利用一元二次方程的根的判别式即可求 【解答】解： 由根的判别式得，△＝b2﹣4ac＝k2+8＞0 故有两个不相等的实数根 故选：A． 【点评】此题主要考查一元二次方程的根的判别式，利用一元二次方程根的判别式（△ 第 11页（共 27页） ＝b2﹣4ac）可以判断方程的根的情况：一元二次方程的根与根的判别式 有如下关系： ① 当△＞0 时，方程有两个不相等的实数根； ② 当△＝0 时，方程有两个相等的实数根； ③ 当△＜0 时，方程无实数根，但有 2 个共轭复根．上述结论反过来也成立． 二、填空题（本大题共有 8 小题，每小题 3 分，共 24 分.不需写出解答过程，请将答案直接 写在答题卡的相应位置上） 9．（3 分）如图，直线 a∥b，∠1＝50°，那么∠2＝ 50 °． 【分析】直接利用平行线的性质分析得出答案． 【解答】解：∵a∥b，∠1＝50°， ∴∠1＝∠2＝50°， 故答案为：50． 【点评】此题主要考查了平行线的性质，正确掌握平行线的性质是解题关键． 10．（3 分）分解因式：x2﹣1＝ （x+1）（x﹣1） ． 【分析】利用平方差公式分解即可求得答案． 【解答】解：x2﹣1＝（x+1）（x﹣1）． 故答案为：（x+1）（x﹣1）． 【点评】此题考查了平方差公式分解因式的知识．题目比较简单，解题需细心． 11．（3 分）如图，转盘中 6 个扇形的面积都相等．任意转动转盘 1 次，当转盘停止转动时， 指针落在阴影部分的概率为 ． 【分析】首先确定在图中阴影区域的面积在整个面积中占的比例，根据这个比例即可求 出指针指向阴影区域的概率． 【解答】解：∵圆被等分成 6 份，其中阴影部分占 3 份， 第 12页（共 27页） ∴落在阴影区域的概率为 ， 故答案为： ． 【点评】本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用 阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例 即事件（A）发生的概率． 12．（3 分）甲、乙两人在 100 米短跑训练中，某 5 次的平均成绩相等，甲的方差是 0.14s2， 乙的方差是 0.06s2，这 5 次短跑训练成绩较稳定的是 乙 ．（填“甲”或“乙”） 【分析】根据方差的意义可作出判断．方差是用来衡量一组数据波动大小的量，方差越 小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定． 【解答】解：∵甲的方差为 0.14s2，乙的方差为 0.06s2， ∴S 甲 2＞S 乙 2， ∴成绩较为稳定的是乙； 故答案为：乙． 【点评】本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表 明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组 数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定． 13．（3 分）设 x1、x2 是方程 x2﹣3x+2＝0 的两个根，则 x1+x2﹣x1•x2＝ 1 ． 【分析】由韦达定理可知 x1+x2＝3，x1•x2＝2，代入计算即可； 【解答】解：x1、x2 是方程 x2﹣3x+2＝0 的两个根， ∴x1+x2＝3，x1•x2＝2， ∴x1+x2﹣x1•x2＝3﹣2＝1； 故答案为 1； 【点评】本题考查一元二次方程根与系数的关系；牢记韦达定理是解题的关键． 14．（3 分）如图，点 A、B、C、D、E 在 ⊙ O 上，且 为 50°，则∠E+∠C＝ 155 °． 第 13页（共 27页） 【分析】连接 EA，根据圆周角定理求出∠BEA，根据圆内接四边形的性质得到∠DEA+ ∠C＝180°，结合图形计算即可． 【解答】解：连接 EA， ∵ 为 50°， ∴∠BEA＝25°， ∵四边形 DCAE 为 ⊙ O 的内接四边形， ∴∠DEA+∠C＝180°， ∴∠DEB+∠C＝180°﹣25°＝155°， 故答案为：155． 【点评】本题考查的是圆内接四边形的性质、圆周角定理，掌握圆内接四边形的对角互 补是解题的关键． 15．（3 分）如图，在△ABC 中，BC＝ + ，∠C＝45°，AB＝ AC，则 AC 的长为 2 ． 【分析】过点 A 作 AD⊥BC，垂足为点 D，设 AC＝x，则 AB＝ x，在 Rt△ACD 中，通 过解直角三角形可得出 AD，CD 的长，在 Rt△ABD 中，利用勾股定理可得出 BD 的长， 由 BC＝BD+CD 结合 BC＝ + 可求出 x 的值，此题得解． 【解答】解：过点 A 作 AD⊥BC，垂足为点 D，如图所示． 第 14页（共 27页） 设 AC＝x，则 AB＝ x． 在 Rt△ACD 中，AD＝AC•sinC＝ x， CD＝AC•cosC＝ x； 在 Rt△ABD 中，AB＝ x，AD＝ x， ∴BD＝ ＝ ． ∴BC＝BD+CD＝ x+ x＝ + ， ∴x＝2． 故答案为：2． 【点评】本题考查了解直角三角形、勾股定理以及解一元一次方程，通过解直角三角形 及勾股定理，找出 BC 与 AC 之间的关系是解题的关键． 16．（3 分）如图，在平面直角坐标系中，一次函数 y＝2x﹣1 的图象分别交 x、y 轴于点 A、 B，将直线 AB 绕点 B 按顺时针方向旋转 45°，交 x 轴于点 C，则直线 BC 的函数表达式 是 y＝ x﹣1 ． 【分析】根据已知条件得到 A（ ，0），B（0，﹣1），求得 OA＝ ，OB＝1，过 A 作 AF ⊥AB 交 BC 于 F，过 F 作 FE⊥x 轴于 E，得到 AB＝AF，根据全等三角形的性质得到 AE ＝OB＝1，EF＝OA＝ ，求得 F（ ，﹣ ），设直线 BC 的函数表达式为：y＝kx+b，解 方程组于是得到结论． 【解答】解：∵一次函数 y＝2x﹣1 的图象分别交 x、y 轴于点 A、B， ∴令 x＝0，得 y＝﹣2，令 y＝0，则 x＝1， 第 15页（共 27页） ∴A（ ，0），B（0，﹣1）， ∴OA＝ ，OB＝1， 过 A 作 AF⊥AB 交 BC 于 F，过 F 作 FE⊥x 轴于 E， ∵∠ABC＝45°， ∴△ABF 是等腰直角三角形， ∴AB＝AF， ∵∠OAB+∠ABO+∠OAB+∠EAF＝90°， ∴∠ABO＝∠EAF， ∴△ABO≌△AFE（AAS）， ∴AE＝OB＝1，EF＝OA＝ ， ∴F（ ，﹣ ）， 设直线 BC 的函数表达式为：y＝kx+b， ∴ ， ∴ ， ∴直线 BC 的函数表达式为：y＝ x﹣1， 故答案为：y＝ x﹣1． 【点评】本题考查了一次函数图象与几何变换，待定系数法求函数的解析式，全等三角 形的判定和性质，正确的作出辅助线是解题的关键． 三、解答题（本大题共有 11 小题，共 102 分，请在答题卡指定区域内作答，解答时应写出 文字说明、推理过程或演算步骤） 17．（6 分）计算：|﹣2|+（sin36°﹣ ）0﹣ +tan45°． 第 16页（共 27页） 【分析】首先对绝对值方、零次幂、二次根式、特殊角三角函数分别进行计算，然后根 据实数的运算法则求得计算结果， 【解答】解：原式＝2+1﹣2+1＝2． 【点评】本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题 目的关键是熟记特殊角的三角函数值，熟练掌握负整数指数幂、二次根式、绝对值等考 点的运算． 18．（6 分）解不等式组： 【分析】分别求出各不等式的解集，再求出其公共解集即可． 【解答】解： 解不等式 ① ，得 x＞1， 解不等式 ② ，得 x≥﹣2， ∴不等式组的解集是 x＞1． 【点评】本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中 间找；大大小小找不到”的原则是解答此题的关键． 19．（8 分）如图，一次函数 y＝x+1 的图象交 y 轴于点 A，与反比例函数 y＝ （x＞0）的 图象交于点 B（m，2）． （1）求反比例函数的表达式； （2）求△AOB 的面积． 【分析】（1）根据一次函数 y＝x+1 的图象交 y 轴于点 A，与反比例函数 y＝ （x＞0） 的图象交于点 B（m，2），可以求得点 B 的坐标，进而求得反比例函数的解析式； （2）根据题目中一次函数的解析式可以求得点 A 的坐标，再根据（1）中求得的点 B 的 坐标，即可求得△AOB 的面积． 【解答】解：（1）∵点 B（m，2）在直线 y＝x+1 上， 第 17页（共 27页） ∴2＝m+1，得 m＝1， ∴点 B 的坐标为（1，2）， ∵点 B（1，2）在反比例函数 y＝ （x＞0）的图象上， ∴2＝ ，得 k＝2， 即反比例函数的表达式是 y＝ ； （2）将 x＝0 代入 y＝x+1，得 y＝1， 则点 A 的坐标为（0，1）， ∵点 B 的坐标为（1，2）， ∴△AOB 的面积是； ． 【点评】本题考查反比例函数与一次函数的交点问题，解答本题的关键是明确题意，利 用数形结合的思想解答． 20．（8 分）在一个不透明的布袋中，有 2 个红球，1 个白球，这些球除颜色外都相同． （1）搅匀后从中任意摸出 1 个球，摸到红球的概率是 ． （2）搅匀后先从中任意摸出 1 个球（不放回），再从余下的球中任意摸出 1 个球．求两 次都摸到红球的概率．（用树状图或表格列出所有等可能出现的结果） 【分析】（1）直接利用概率公式求解； （2）画树状图展示所有 6 种等可能的结果数，找出两次都摸到红球的结果数，然后根据 概率公式求解． 【解答】解：（1）搅匀后从中任意摸出 1 个球，摸到红球的概率＝ ；、 故答案为 ； （2）画树状图为： 共有 6 种等可能的结果数，其中两次都摸到红球的结果数为 2， 所以两次都摸到红球的概率＝ ＝ ． 【点评】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果 n， 再从中选出符合事件 A 或 B 的结果数目 m，然后利用概率公式计算事件 A 或事件 B 的概 第 18页（共 27页） 率． 21．（8 分）如图，AD 是△ABC 的角平分线． （1）作线段 AD 的垂直平分线 EF，分别交 AB、AC 于点 E、F；（用直尺和圆规作图， 标明字母，保留作图痕迹，不写作法．） （2）连接 DE、DF，四边形 AEDF 是 菱 形．（直接写出答案） 【分析】（1）利用尺规作线段 AD 的垂直平分线即可． （2）根据四边相等的四边形是菱形即可证明． 【解答】解：（1）如图，直线 EF 即为所求． （2）∵AD 平分∠ABC， ∴∠BAD＝∠CAD， ∴∠BAD＝∠CAD， ∵∠AOE＝∠AOF＝90°，AO＝AO， ∴△AOE≌△AOF（ASA）， ∴AE＝AF， ∵EF 垂直平分线段 AD， ∴EA＝ED，FA＝FD， ∴EA＝ED＝DF＝AF， ∴四边形 AEDF 是菱形． 故答案为菱． 【点评】本题考查作图﹣基本作图，线段的垂直平分线，全等三角形的判定和性质等知 识，解题的关键是熟练掌握基本知识，属于中考常考题型． 第 19页（共 27页） 22．（10 分）体育器材室有 A、B 两种型号的实心球，1 只 A 型球与 1 只 B 型球的质量共 7 千克，3 只 A 型球与 1 只 B 型球的质量共 13 千克． （1）每只 A 型球、B 型球的质量分别是多少千克？ （2）现有 A 型球、B 型球的质量共 17 千克，则 A 型球、B 型球各有多少只？ 【分析】（1）直接利用 1 只 A 型球与 1 只 B 型球的质量共 7 千克，3 只 A 型球与 1 只 B 型球的质量共 13 千克得出方程求出答案； （2）利用分类讨论得出方程的解即可． 【解答】解：（1）设每只 A 型球、B 型球的质量分别是 x 千克、y 千克，根据题意可得： ， 解得： ， 答：每只 A 型球的质量是 3 千克、B 型球的质量是 4 千克； （2）∵现有 A 型球、B 型球的质量共 17 千克， ∴设 A 型球 1 个，设 B 型球 a 个，则 3+4a＝17， 解得：a＝ （不合题意舍去）， 设 A 型球 2 个，设 B 型球 b 个，则 6+4b＝17， 解得：b＝ （不合题意舍去）， 设 A 型球 3 个，设 B 型球 c 个，则 9+4c＝17， 解得：c＝2， 设 A 型球 4 个，设 B 型球 d 个，则 12+4d＝17， 解得：d＝ （不合题意舍去）， 设 A 型球 5 个，设 B 型球 e 个，则 15+4e＝17， 解得：a＝ （不合题意舍去）， 综上所述：A 型球、B 型球各有 3 只、2 只． 【点评】此题主要考查了二元一次方程组的应用，正确分类讨论是解题关键． 23．（10 分）某公司共有 400 名销售人员，为了解该公司销售人员某季度商品销售情况，随 机抽取部分销售人员该季度的销售数量，并把所得数据整理后绘制成如下统计图表进行 分析． 第 20页（共 27页） 频数分布表 组别 销售数量（件） 频数 频率 A 20≤x＜40 3 0.06 B 40≤x＜60 7 0.14 C 60≤x＜80 13 a D 80≤x＜100 m 0.46 E 100≤x＜120 4 0.08 合计 b 1 请根据以上信息，解决下列问题： （1）频数分布表中，a＝ 0.26 、b＝ 50 ； （2）补全频数分布直方图； （3）如果该季度销量不低于 80 件的销售人员将被评为“优秀员工”，试估计该季度被评 为“优秀员工”的人数． 【分析】（1）由频数除以相应的频率求出 b 的值，进而确定出 a 的值即可； （2）补全频数分布直方图即可； （3）求出不低于 80 件销售人员占的百分比，乘以 400 即可得到结果． 【解答】解：（1）根据题意得：b＝3÷0.06＝50，a＝ ＝0.26； 故答案为：0.26；50； （2）根据题意得：m＝50×0.46＝23， 补全频数分布图，如图所示： 第 21页（共 27页） （3）根据题意得：400×（0.46+0.08）＝216， 则该季度被评为“优秀员工”的人数为 216 人． 【点评】此题考查了频数分布直方图，用样本估计总体，以及频数分布图，弄清题中的 数据是解本题的关键． 24．（10 分）如图，在 Rt△ABC 中，∠ACB＝90°，CD 是斜边 AB 上的中线，以 CD 为直 径的 ⊙ O 分别交 AC、BC 于点 M、N，过点 N 作 NE⊥AB，垂足为 E． （1）若 ⊙ O 的半径为 ，AC＝6，求 BN 的长； （2）求证：NE 与 ⊙ O 相切． 【分析】（1）由直角三角形的性质可求 AB＝10，由勾股定理可求 BC＝8，由等腰三角形 的性质可得 BN＝4； （2）欲证明 NE 为 ⊙ O 的切线，只要证明 ON⊥NE． 【解答】解：（1）连接 DN，ON 第 22页（共 27页） ∵ ⊙ O 的半径为 ， ∴CD＝5 ∵∠ACB＝90°，CD 是斜边 AB 上的中线， ∴BD＝CD＝AD＝5， ∴AB＝10， ∴BC＝ ＝8 ∵CD 为直径 ∴∠CND＝90°，且 BD＝CD ∴BN＝NC＝4 （2）∵∠ACB＝90°，D 为斜边的中点， ∴CD＝DA＝DB＝ AB， ∴∠BCD＝∠B， ∵OC＝ON， ∴∠BCD＝∠ONC， ∴∠ONC＝∠B， ∴ON∥AB， ∵NE⊥AB， ∴ON⊥NE， ∴NE 为 ⊙ O 的切线． 【点评】本题考查切线的判定和性质，解直角三角形等知识，解题的关键是熟练掌握基 本知识，属于中考常考题型． 25．（10 分）如图 ① 是一张矩形纸片，按以下步骤进行操作： （Ⅰ）将矩形纸片沿 DF 折叠，使点 A 落在 CD 边上点 E 处，如图 ② ； （Ⅱ）在第一次折叠的基础上，过点 C 再次折叠，使得点 B 落在边 CD 上点 B′处，如 图 ③ ，两次折痕交于点 O； （Ⅲ）展开纸片，分别连接 OB、OE、OC、FD，如图 ④ ． 【探究】 （1）证明：△OBC≌△OED； （ 2 ） 若 AB ＝ 8 ， 设 BC 为 x ， OB2 为 y ， 求 y 关 于 x 的 关 系 式 ． 第 23页（共 27页） 【分析】（1）利用折叠性质，由边角边证明△OBC≌△OED； （2）过点 O 作 OH⊥CD 于点 H．由（1）△OBC≌△OED，OE＝OB，BC＝x，则 AD＝ DE＝x，则 CE＝8﹣x，OH＝ CD＝4，则 EH＝CH﹣CE＝4﹣（8﹣x）＝x﹣4 在 Rt△ OHE 中，由勾股定理得 OE2＝OH2+EH2，即 OB2＝42+（x﹣4）2，所以 y 关于 x 的关系 式：y＝x2﹣8x+32． 【解答】解：（1）证明：由折叠可知，AD＝ED，∠BCO＝∠DCO＝∠ADO＝∠CDO＝ 45° ∴BC＝DE，∠COD＝90°，OC＝OD， 在△OBC≌△OED 中， ， ∴△OBC≌△OED（SAS）； （2）过点 O 作 OH⊥CD 于点 H． 由（1）△OBC≌△OED， OE＝OB， ∵BC＝x，则 AD＝DE＝x， ∴CE＝8﹣x， ∵OC＝OD，∠COD＝90° ∴CH＝ CD＝ AB＝ ＝4， 第 24页（共 27页） OH＝ CD＝4， ∴EH＝CH﹣CE＝4﹣（8﹣x）＝x﹣4 在 Rt△OHE 中，由勾股定理得 OE2＝OH2+EH2， 即 OB2＝42+（x﹣4）2， ∴y 关于 x 的关系式：y＝x2﹣8x+32． 【点评】本题是四边形综合题，熟练运用轴对称的性质和全等三角形的判定以及勾股定 理是解题的关键． 26．（12 分）【生活观察】甲、乙两人买菜，甲习惯买一定质量的菜，乙习惯买一定金额的 菜，两人每次买菜的单价相同，例如： 第一次 菜价 3 元/千克 质量 金额 甲 1 千克 3 元 乙 1 千克 3 元 第二次： 菜价 2 元/千克 质量 金额 甲 1 千克 2 元 乙 1.5 千克 3 元 （1）完成上表； （2）计算甲两次买菜的均价和乙两次买菜的均价．（均价＝总金额÷总质量） 【数学思考】设甲每次买质量为 m 千克的菜，乙每次买金额为 n 元的菜，两次的单价分 别是 a 元/千克、b 元/千克，用含有 m、n、a、b 的式子，分别表示出甲、乙两次买菜的 均价 、 ，比较 、 的大小，并说明理由． 【知识迁移】某船在相距为 s 的甲、乙两码头间往返航行一次．在没有水流时，船的速 度为 v，所需时间为 t1；如果水流速度为 p 时（p＜v），船顺水航行速度为（v+p），逆水 第 25页（共 27页） 航行速度为（v﹣p），所需时间为 t2．请借鉴上面的研究经验，比较 t1、t2 的大小，并说 明理由． 【分析】（1）利用均价＝总金额÷总质量可求； （2）利用均价＝总金额÷总质量可求甲两次买菜的均价和乙两次买菜的均价； 【数学思考】分别表示出 、 ，然后求差，把分子配方，利用偶次方的非负性可得 答案； 【知识迁移】分别表示出 、 ，然后求差，判断分式的值总小于等于 0，从而得结 论． 【解答】解：（1）2×1＝2（元），3÷2＝1.5（元/千克） 故答案为 2；1.5． （2）甲两次买菜的均价为：（3+2）÷2＝2.5（元/千克） 乙两次买菜的均价为：（3+3）÷（1+1.5）＝2.4（元/千克） ∴甲两次买菜的均价为 2.5（元/千克），乙两次买菜的均价为 2.4（元/千克）． 【数学思考】 ＝ ＝ ， ＝ ＝ ∴ ﹣ ═ ﹣ ＝ ≥0 ∴ ≥ 【知识迁移】t1＝ ，t2＝ + ＝ ∴t1﹣t2═ ﹣ ＝ ∵p＜v ∴t1﹣t2≤0（当且仅当 p＝0 时取等号） ∴t1≤t2． 【点评】本题主要考查了均价＝总金额÷总质量的基本计算方法，以及分式加减运算和 完全平方公式在计算中的应用，本题计算量较大． 27．（14 分）如图所示，二次函数 y＝k（x﹣1）2+2 的图象与一次函数 y＝kx﹣k+2 的图象交 于 A、B 两点，点 B 在点 A 的右侧，直线 AB 分别与 x、y 轴交于 C、D 两点，其中 k＜0． （1）求 A、B 两点的横坐标； 第 26页（共 27页） （2）若△OAB 是以 OA 为腰的等腰三角形，求 k 的值； （3）二次函数图象的对称轴与 x 轴交于点 E，是否存在实数 k，使得∠ODC＝2∠BEC， 若存在，求出 k 的值；若不存在，说明理由． 【分析】（1）将二次函数与一次函数联立得：k（x﹣1）2+2＝kx﹣k+2，即可求解； （2）分 OA＝AB、OA＝OB 两种情况，求解即可； （3）求出 m＝﹣k2﹣k ，在△AHM 中，tan α ＝ ＝ ＝k+ ＝tan∠BEC ＝ ＝k+2，即可求解． 【解答】解：（1）将二次函数与一次函数联立得：k（x﹣1）2+2＝kx﹣k+2， 解得：x＝1 或 2， 故点 A、B 的坐标分别为（1，2）、（2，k+2）； （2）OA＝ ＝ ， ① 当 OA＝AB 时， 即：1+k2＝5，解得：k＝±2（舍去 2）； ② 当 OA＝OB 时， 4+（k+2）2＝5，解得：k＝﹣1 或﹣3； 故 k 的值为：﹣1 或﹣2 或﹣3； （3）存在，理由： 过点 B 作 BH⊥AE 于点 H，将△AHB 的图形放大见右侧图形， 过点 A 作∠HAB 的角平分线交 BH 于点 M，过点 M 作 MN⊥AB 于点 N，过点 B 作 BK⊥ x 轴于点 K， 第 27页（共 27页） 图中：点 A（1，2）、点 B（2，k+2），则 AH＝﹣k，HB＝1， 设：HM＝m＝MN，则 BM＝1﹣m， 则 AN＝AH＝﹣k，AB＝ ，NB＝AB﹣AN， 由勾股定理得：MB2＝NB2+MN2， 即：（1﹣m）2＝m2+（ +k）2， 解得：m＝﹣k2﹣k ， 在△AHM 中，tan α ＝ ＝ ＝k+ ＝tan∠BEC＝ ＝k+2， 解得：k＝ （舍去正值）， 故 k＝﹣ ． 【点评】本题为二次函数综合应用题，涉及到一次函数、解直角三角形的知识，其中（3）， 通过 tan2 α 求出 tan α ，是此类题目求解的一般方法． 声明：试 题解析著作权 属菁优网所有 ，未经书面同 意，不得复制 发布 日期：2019/6/22 19:56:51 ；用户： 刘全红；邮箱 ：13714238242 ；学号：27536937