阜新市2014年中考数学卷 6页

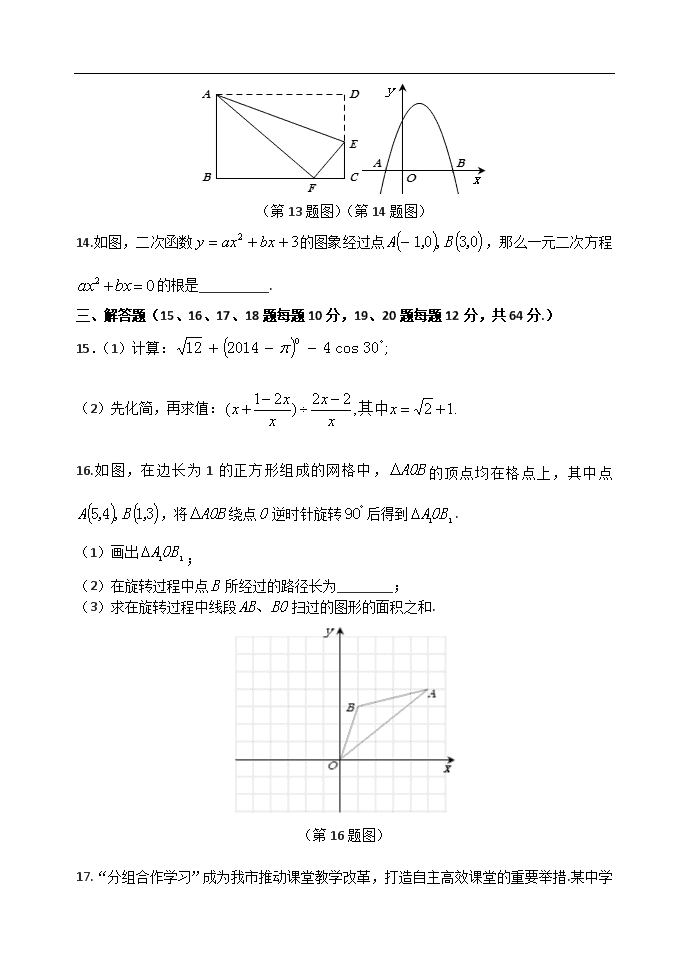
‎2014年阜新市初中毕业生学业考试 数学试卷 考试时间100分钟试卷满分100分 各位考生请注意：务必将试题答案写在答题卡对应的位置上，否则不得分，千万记住哦！！‎ 一、选择题（在每一小题给出的四个选项中，只有一个是正确的.每小题3分，共18分.）‎ ‎1．的倒数是 ‎ A． B. C. D.‎ ‎2.如图的几何体是由4个完全相同的正方体组成的，这个几何体的左视图是 ‎ ‎ ‎（第2题图） A B C D ‎3.在某校开展的“厉行节约，你我有责”活动中，七年级某班对学生7天内收集饮料瓶的情况统计如下（单位：个）：76，90，64，100，84，64，73.则这组数据的众数和中位数分别是 A．64，100 B. 64，76 C. 76，64 D.64，84‎ ‎4．与在平面直角坐标系中的位置如图所示，它们关于点成中心对称，其中点，则点的坐标是 A． B. ‎ C. D.‎ ‎（第4题图）‎ ‎5.反比例函数在每个象限内的函数值随的增大而增大，则的取值范围是 A． B. C. D.‎ 考生请注意：6、7题为二选一的选做题，即只能选做其中一个题目.‎ 多答时只按作答的首题评分，切记！‎ ‎6.为了节省空间，家里的饭碗一般是摞起来存放的.如果6只饭碗摞起来的高度为15cm，9只饭碗摞起来的高度为20cm，那么11只饭碗摞起来的高度更接近 A．21cm B. 22cm C. 23cm D.24cm ‎7.对于一次函数，下列叙述正确的是 A．当时，函数图象经过第一、二、三象限 B．当时，随的增大而减小 C．当时，函数图象一定交于轴的负半轴 D．函数图象一定经过点 二、填空题（每小题3分，共18分.）‎ ‎8.函数的自变量的取值范围是_________.‎ ‎9.任意掷一枚质地均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6），朝上的面的数字大于2的概率是________.‎ ‎10.如图，直线∥，，如果，那么_______度.‎ ‎（第10题图）（第11题图）‎ ‎11.如图，是⊙的内接三角形，如果，那么_______度.‎ ‎12.已知∽，其中，那么的周长是________.‎ 考生请注意：13、14题为二选一的选做题，即只能选做其中一个题目.多答时只按作答的首题评分，切记！‎ ‎13.如图，将矩形沿折叠，点恰好落在边上的点处，如果，那么值是________.‎ ‎（第13题图）（第14题图）‎ ‎14.如图，二次函数的图象经过点，那么一元二次方程的根是__________.‎ 三、解答题（15、16、17、18题每题10分，19、20题每题12分，共64分.）‎ ‎15．（1）计算：‎ ‎（2）先化简，再求值：‎ ‎16.如图，在边长为1的正方形组成的网格中，的顶点均在格点上，其中点，将绕点逆时针旋转后得到.‎ ‎（1）画出；‎ ‎（2）在旋转过程中点所经过的路径长为________；‎ ‎（3）求在旋转过程中线段扫过的图形的面积之和.‎ ‎（第16题图）‎ ‎17.“分组合作学习”成为我市推动课堂教学改革，打造自主高效课堂的重要举措.‎ 某中学从全校学生中随机抽取100人作为样本，对“分组合作学习”实施前后学生的学习兴趣变化情况进行调查分析，统计如下：‎ 分组前学生学习兴趣分组后学生学习兴趣 ‎（第17题图）‎ 请结合图中信息解答下列问题：‎ ‎（1）求出分组前学生学习兴趣为“高”的所占的百分比为_________；‎ ‎（2）补全分组后学生学习兴趣的统计图；‎ ‎（3）通过“分组合作学习”前后对比，请你估计全校2000名学生中学习兴趣获得提高的学生有多少人？请根据你的估计情况谈谈对“分组合作学习”这项举措的看法.‎ ‎18.在“玉龙”自行车队的一次训练中，1号队员以高于其他队员10千米/时的速度独自前行，匀速行进一段时间后，又返回队伍，在往返过程中速度保持不变.设分开后行进的时间为（时），1号队员和其他队员行进的路程分别为（千米），并且与的函数关系如图所示：‎ ‎（第18题图）‎ ‎（1）1号队员折返点的坐标为__________，如果1号队员与其他队员经过t小时相遇，那么点的坐标为__________；（用含t的代数式表示）‎ ‎（2）求1号队员与其他队员经过几小时相遇？‎ ‎（3）在什么时间内，1号队员与其他队员之间的距离大于2千米？‎ ‎19.已知，在矩形中，连接对角线，将绕点顺时针旋转得到 ‎，并将它沿直线向左平移，直线与交于点，连接，.‎ ‎（1）如图①，当，点平移到线段上时，线段有怎样的数量关系和位置关系？直接写出你的猜想；‎ ‎（2）如图②，当，点平移到线段的延长线上时，（1）中的结论是否成立，请说明理由；‎ ‎（3）如图③，当时，对矩形进行如已知同样的变换操作，线段有怎样的数量关系和位置关系？直接写出你的猜想.‎ 图① 图② 图③‎ ‎（第19题图）‎ ‎20.如图，抛物线交轴于点，交轴于点，已知经过点的直线的表达式为.‎ ‎（1）求抛物线的函数表达式及其顶点的坐标；‎ ‎（2）如图①，点是线段上的一个动点，其中，作直线轴，交直线于，交抛物线于，作∥轴，交直线于点，四边形为矩形.设矩形的周长为，写出与的函数关系式，并求为何值时周长最大；‎ ‎（3）如图②，在抛物线的对称轴上是否存在点，使点构成的三角形是以为腰的等腰三角形.若存在，直接写出所有符合条件的点的坐标；若不存在，请说明理由.‎ ‎ ‎ 图① 图②‎ ‎（第20题图）‎