中考二轮复习之证明两角相等的方法 19页

中考二轮复习之证明两角相等的方法 ‎【相关定理或常见结论】‎ ‎1、相交线、平行线：‎ ‎（1）对顶角相等；‎ ‎（2）等角的余角（或补角）相等；‎ ‎（3）两直线平行，同位角相等、内错角相等；‎ ‎（4）凡直角都相等；‎ ‎（5）角的平分线分得的两个角相等.‎ ‎2、三角形 ‎（1）等腰三角形的两个底角相等；‎ ‎（2）等腰三角形底边上的高（或中线）平分顶角（三线合一）；‎ ‎（3）三角形外角和定理：三角形外角等于和它不相邻的内角之和 ‎（4）全等三角形的对应角相等；‎ ‎（5）相似三角形的对应角相等.‎ ‎3、四边形 ‎（1）平行四边形的对角相等；‎ ‎（2）菱形的每一条对角线平分一组对角；‎ ‎（3）等腰梯形在同一底上的两个角相等.‎ ‎4、圆 ‎（1）在同圆或等圆中，若有两条弧相等或有两条弦相等，那么它们所对的圆心角相等；‎ ‎（2）在同圆或等圆中，同弧或等弧所对的圆周角相等. ，圆心角相等.‎ ‎（3）圆周角定理：在同圆或等圆中，一条弧所对的圆周角等于它所对的圆心角的一半.‎ ‎（4）圆内接四边形的性质：圆内接四边形的对角互补;并且每一个外角都等于它的内对角.‎ ‎（5）三角形的内心的性质：三角形的内心与角顶点的连线平分这个角.‎ ‎（6）正多边形的性质：正多边形的外角等于它的中心角.‎ ‎（7）从圆外一点引圆的两条切线，圆心和这一点的连线平分这两条切线的夹角；‎ ‎5、利用等量代换、等式性质 证明两角相等.‎ ‎6、利用三角函数计算出角的度数相等 ‎【典题精析】‎ ‎（一） 利用全等相关知识证明角相等 例1 已知：如图，于点，于点，与交于点，且．‎ ‎ 求证：平分．‎ 例2 如图，在四边形ABCD中，AD∥BC，E是四边形内一点，ED⊥AD，BE=DC，∠ECB=45 ‎ 求证：∠EBC＝∠EDC 例3 如图，已知四边形ABCD中AC=BD，CD∥BA，四边形AEBC是平行四边形．‎ 求证：∠ABD＝∠ABE．‎ ‎（二）利用平行、三角形的内角和、外角关系证明角之间的关系 例4．已知：△ABC中，AD是高，CE是中线，DC=BE，DG⊥CE，G是垂足， ‎ 求证：⑴G是CE的中点；⑵∠B=2∠BCE. ‎ 例5 如图，直线，连结，直线及线段把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点落在某个部分时，连结，构成，，三个角．（提示：有公共端点的两条重合的射线所组成的角是角．）‎ ‎（1）当动点落在第①部分时，求证：；‎ ‎（2）当动点落在第②部分时，是否成立（直接回答成立或不成立）？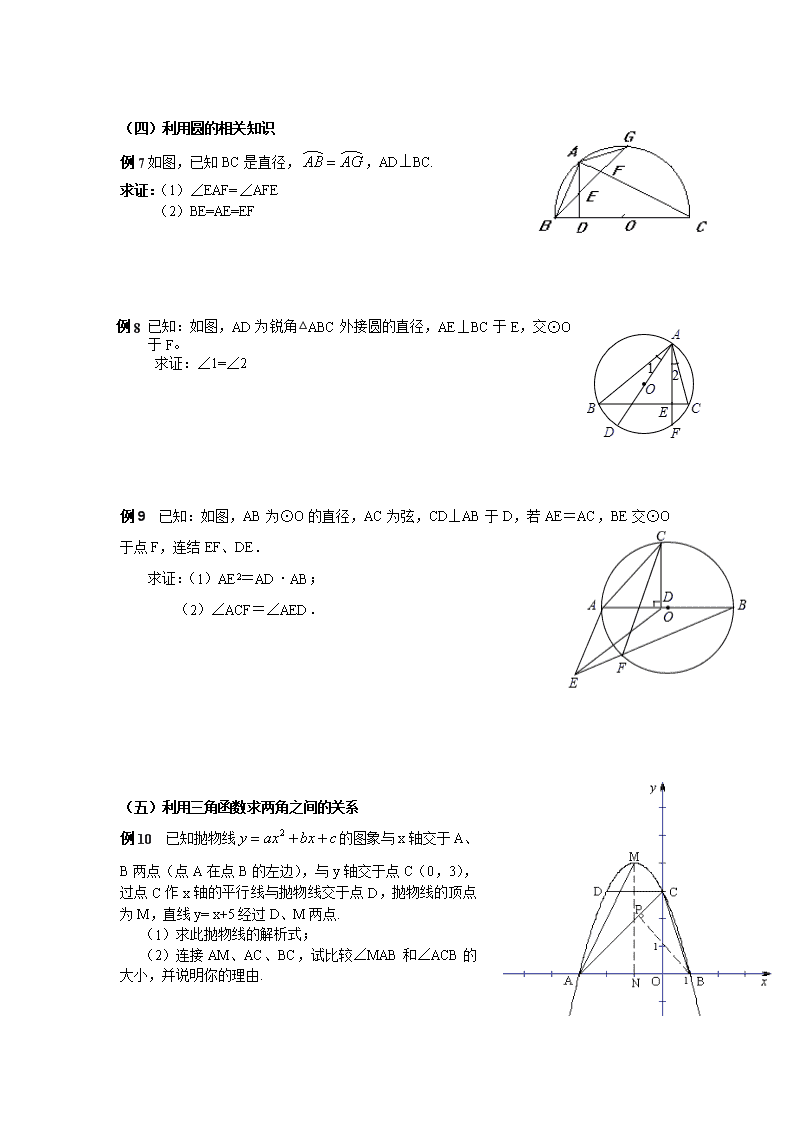‎ ‎①‎ ‎②‎ ‎③‎ ‎①‎ ‎②‎ ‎③‎ ‎④‎ ‎①‎ ‎②‎ ‎③‎ ‎④‎ ‎④‎ ‎（3）当动点在第③部分时，全面探究，，之间的关系，并写出动点的具体位置和相应的结论．选择其中一种结论加以证明．‎ ‎（三）利用四边形的相关知识证明角的有关问题 例6 已知：如图，在△ABC中，AB＝AC，E是AB的中点，以点E为圆心，EB为半径画弧，交BC于点D，连结ED，并延长ED到点F，使，连结FC．求证：∠F＝∠A．‎ ‎（四）利用圆的相关知识 例7如图，已知BC是直径，，AD⊥BC.‎ 求证：（1）∠EAF=∠AFE ‎ （2）BE=AE=EF 例8 已知：如图，AD为锐角△ABC外接圆的直径，AE⊥BC于E，交⊙O于F。‎ ‎ 求证：∠1=∠2‎ 例9　已知：如图，AB为⊙O的直径，AC为弦，CD⊥AB于D，若AE＝AC，BE交⊙O于点F，连结EF、DE．‎ ‎　　求证：（1）AE2＝AD·AB；‎ ‎　　（2）∠ACF＝∠AED．‎ ‎（五）利用三角函数求两角之间的关系 例10 已知抛物线的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C（0，3），过点C作x轴的平行线与抛物线交于点D，抛物线的顶点为M，直线y= x+5经过D、M两点.‎ ‎（1）求此抛物线的解析式；‎ ‎（2）连接AM、AC、BC，试比较∠MAB和∠ACB的大小，并说明你的理由.‎ ‎【智能巧练】‎ ‎⒈如图，△ABC中，∠B的平分线与∠ACB的外角平分线相交于点D，则∠D与 ‎∠A的比是________‎ ‎⒉.已知，如图，在△ABC中，AC2=AD AB。‎ 求证：∠ACD=∠ABC。 ‎ ‎⒊ 如图，已知：平行四边形ABCD中，E是CA延长线上的点，‎ F是AC延长线上的点，且AE=CF 求证：⑴∠E=∠F；‎ ‎⑵BE=DF ‎⒋ 如图，△ABC中，高BD、CE交于点F，且CG=AB，BF=AC，连接AF， ‎ 求证：AG⊥AF ‎ ‎ ‎ 第4题 第5题 ‎ ‎⒌ Rt△ABC中，∠A=90°，AB=AC，D为BC上任意一点，DF⊥AB，DE⊥AC，垂足分别为F、E，M为BC中点，试判断△MEF是什么形状的三角形，并说明之.‎ B C D E A F ‎6．已知：如图，AD是△ABC外角∠EAC的平分线，交BC的延长线于点D. 延长DA交△ABC的外接圆于点F.‎ ‎ ⑴求证：∠FBC=∠FCB；‎ ‎⑵若，求FB的长.‎ 图(1)‎ B O A F D C G E l ‎·‎ ‎7．⑴如图，已知直线AB过圆心O，交⊙O于A、B，直线AF交⊙O于F（不与B重合），直线l交⊙O于C、D，交AB于E，且与AF垂直，垂足为G，连结AC、AD．‎ 求证：①∠BAD＝∠CAG；②AC·AD＝AE·AF．‎ ‎⑵在问题⑴中，直线l向下平行移动，与⊙O相切，其他条件不变．‎ ‎①请你画出变化后的图形，并对照图，标记字母；‎ ‎②问题⑴中的两个结论是否仍成立？如果成立，请给出证明；如果不成立，请说明理由．‎ ‎ ‎ ‎8．如图，⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D，DF⊥AC，垂足为F，DE⊥BC，垂足为E，给出下列4个结论：‎ ‎①CE=CF；②∠ACB=∠EDF；③DE是⊙O的切线；④=；‎ 其中一定成立的是（ ）‎ A. ①②③ B. ②③④ C. ①③④ D . ①②④‎ ‎9．已知，如图，在四边形ABCD中，AB=DC，E、F分别为BC、AD的中点，BA、CD的延长线分别与EF的延长线交于K、H 求证：∠BKE=∠CHE ‎10．已知：AB是⊙O的直径，弦CD⊥AB于M，点E是上一动点.‎ ‎⑴ 如图1，若DE交AB于N，交AC于F，且DE=AC，连结AD、CE，‎ 求证：①∠CED=∠ADE ②=NF·NE ‎⑵ 如图2，若DE与AC的延长线交于F，且DE=AC，那么=NF·NE的结论是否成立？若成立请证明，若不成立请说明理由.‎ ‎ ‎ 图1 图2‎ ‎【自主检测】‎ ‎1．已知如左图，在ABC中, ∠BAC=90°， AB=AC,M为AC的中点，AD⊥BM。‎ 求证:∠AMB=∠DMC ‎ ‎ ‎ 2. 如右图在△ABC中，EF⊥AB，CD⊥AB，G在AC边上并且∠GDC=∠EFB，‎ 求证：∠AGD=∠ACB ‎ ‎ ‎3、如图，△ABC內接于圆，D是弧BC的中点，AD交BC于E，‎ 求证：∠ABD=∠AEC ‎ ‎4、已知：AB是⊙O的直径，C是⊙O上一点，连接AC，过点C作直线CD⊥AB于点D，E是AB上一点，直线CE与⊙O交于点F，连结AF，与直线CD交于点G.‎ 求证：∠ACD=∠F.‎ 证明两角相等的方法 ‎【重点解读】‎ 证明两角相等是中考命题中常见的一种题型，此类证明看似简单，但方法不当也会带来麻烦，特别是在中考有限的两个小时中。恰当选用正确的方法，可取得事半功倍的效果。在教学中总结了一些定理（或常见结论）以及几种处理方法，仅供参考。‎ ‎【相关定理或常见结论】‎ ‎1、相交线、平行线：‎ ‎（1）对顶角相等；‎ ‎（2）等角的余角（或补角）相等；‎ ‎（3）两直线平行，同位角相等、内错角相等；‎ ‎（4）凡直角都相等；‎ ‎（5）角的平分线分得的两个角相等.‎ ‎2、三角形 ‎（1）等腰三角形的两个底角相等；‎ ‎（2）等腰三角形底边上的高（或中线）平分顶角（三线合一）；‎ ‎（3）三角形外角和定理：三角形外角等于和它不相邻的内角之和 ‎（4）全等三角形的对应角相等；‎ ‎（5）相似三角形的对应角相等.‎ ‎3、四边形 ‎（1）平行四边形的对角相等；‎ ‎（2）菱形的每一条对角线平分一组对角；‎ ‎（3）等腰梯形在同一底上的两个角相等.‎ ‎4、圆 ‎（1）在同圆或等圆中，若有两条弧相等或有两条弦相等，那么它们所对的圆心角相等；‎ ‎（2）在同圆或等圆中，同弧或等弧所对的圆周角相等. ，圆心角相等.‎ ‎（3）圆周角定理：在同圆或等圆中，一条弧所对的圆周角等于它所对的圆心角的一半.‎ ‎（4）圆内接四边形的性质：圆内接四边形的对角互补;并且每一个外角都等于它的内对角.‎ ‎（5）三角形的内心的性质：三角形的内心与角顶点的连线平分这个角.‎ ‎（6）正多边形的性质：正多边形的外角等于它的中心角.‎ ‎（7）从圆外一点引圆的两条切线，圆心和这一点的连线平分这两条切线的夹角；‎ ‎5、利用等量代换、等式性质 证明两角相等.‎ ‎6、利用三角函数计算出角的度数相等 ‎【典题精析】‎ ‎（一） 利用全等相关知识证明角相等 例1 已知：如图，于点，于点，与交于点，且．‎ ‎ 求证：平分．‎ 分析：要证平分，因为于点，于点，所以只要证明OD=OE；若能证明若能证△OBD≌△OCE 即可，因为可证 ‎∠ODB=∠OEC=90°,∠BOD=∠COE，而BD=CE，故问题得到解决．‎ 证明：∵于点，于点 ‎∴∠ODB=∠OEC=90°‎ 在△OBD和△OCE中 ‎∠ODB=∠OEC ‎∠BOD=∠COE BD=CE ‎∴△OBD≌△OCE ‎∴OD=OE ‎∵于点，于点 ‎∴平分．‎ 说明：本例的证明运用了对顶角相等，角的平分线性质的逆定理 例2 如图，在梯形ABCD中，AD∥BC，E是梯形内一点，ED⊥AD，BE=DC，∠ECB=45 o．‎ 求证：∠EBC＝∠EDC 分析：要证明∠EBC＝∠EDC，容易想到证全等，而图中没有全等的三角形，如果能构造出两个全等的三角形即可。延长DE与BC交于点于点F， 这样就很容易证△BEF≌△DCF，从而问题得到解决。‎ 证明：延长DE与BC交于点于点F AD∥BC，ED⊥AD ‎ ∴DF⊥BC ‎∴∠BFE=∠DFC=90°‎ ‎∵∠ECB=45 o ‎∴∠ECB=∠CEB=45 o ‎ ∴CF=EF 在Rt△BEF和Rt△DCF中 EF=CF ，BE=DC ‎∴Rt△BEF≌Rt△DCF ‎∴∠EBC＝∠EDC 说明：本例运用全等三角形的对应角相等，来证明两角相等 例3 如图，已知四边形ABCD是等腰梯形，CD∥BA，四边形AEBC是平行四边形．‎ 求证：∠ABD＝∠ABE．‎ 分析：要证∠ABD＝∠ABE，若能证△ABD≌△ABE即可．因为可证BE＝AC＝BD，AE＝BC＝AD，而AB为公共边，故问题得到解决．‎ 证明：∵四边形ABCD是等腰梯形，∴AD＝BC，AC＝BD．‎ ‎∵四边形AEBC是平行四边形，∴BC＝AE，AC＝BE．‎ ‎∴AD＝AE，BD＝BE．‎ 又∵AB＝AB，∴△ABD≌△ABE．‎ ‎∴∠ABD＝∠ABE．‎ 说明：本例通过运用等腰梯形的性质来证明三角形全等从而证明两角相等．‎ 总结：这类题主要考查全等三角形、特殊四边形的性质，在中考中也是常考的题型，在证明过程中，特别要抓住一些基本图形，同时还要注意常用辅助线的作法。‎ ‎（二）利用平行、三角形的内角和、外角关系证明角之间的关系 例4．已知：△ABC中，AD是高，CE是中线，DC=BE，DG⊥CE，G是垂足， ‎ 求证：⑴G是CE的中点；⑵∠B=2∠BCE. ‎ 分析：⑴已知中多垂直和中线条件，‎ 可联想直角三角形斜边上的中线性质；‎ 要证明G是CE的中点，结合已知条件DG⊥CE，‎ 符合等腰三角形三线合一中的两个条件，‎ 故连结DE，证明△DCE是等腰三角形，由DG⊥CE，‎ 可得G是CE的中点.‎ ‎⑵由直角三角形斜边上的中线等于斜边的一半，BE=DE，∠B转化为∠EDB.‎ 证明：⑴连结DE，‎ ‎∵∠ADB=90°，E是AB的中点，‎ ‎∴DE=AE=BE（直角三角形斜边上的中线等于斜边的一半），‎ 又∵DC=BE，∴DC=DE，‎ 又∵DG⊥CE，‎ ‎∴G是CE中点（等腰三角形底边上的高平分底边）.‎ ‎⑵∵DE=DC，∴∠DCE=∠DEC（等边对等角），‎ ‎∴∠EDB=∠DEC+∠DCE=2∠BCE（三角形的外角等于两不相邻内角的和），‎ 又∵DE=BE，∴∠B=∠EDB，∴∠B=2∠BCE 直角三角形、等腰三角形等特殊三角形，其特殊性质有：直角三角形斜边上的中线等于斜边的一半；等腰三角形三线合一的性质通常有以下变形形式：已知等腰和高、已知顶角平分线和高、已知等腰和底边中线. 特殊三角形与线段和角的相等、线段和角的倍半关系有着密切关系.‎ 例5 如图，直线，连结，直线及线段把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点落在某个部分时，连结，构成，，三个角．（提示：有公共端点的两条重合的射线所组成的角是角．）‎ ‎（1）当动点落在第①部分时，求证：；‎ ‎（2）当动点落在第②部分时，是否成立（直接回答成立或不成立）？‎ ‎①‎ ‎②‎ ‎③‎ ‎①‎ ‎②‎ ‎③‎ ‎④‎ ‎①‎ ‎②‎ ‎③‎ ‎④‎ ‎④‎ ‎（3）当动点在第③部分时，全面探究，，之间的关系，并写出动点的具体位置和相应的结论．选择其中一种结论加以证明．‎ 分析：本题主要考查平行线的性质及三角形内角和定理和外角性质 图1‎ ‎（1）解法一：如图1‎ 延长BP交直线AC于点E ‎ ‎∵ AC∥BD , ∴ ∠PEA = ∠PBD . ‎ ‎∵ ∠APB = ∠PAE + ∠PEA , ‎ ‎∴ ∠APB = ∠PAC + ∠PBD . ‎ 图2‎ 解法二：如图2‎ 过点P作FP∥AC , ‎ ‎∴ ∠PAC = ∠APF . ‎ ‎∵ AC∥BD , ∴FP∥BD . ‎ ‎∴ ∠FPB =∠PBD . ‎ 图3‎ ‎ ∴ ∠APB =∠APF +∠FPB =∠PAC + ∠PBD .‎ 解法三：如图3，‎ ‎∵ AC∥BD , ∴ ∠CAB +∠ABD = 180° ‎ 即 ∠PAC +∠PAB +∠PBA +∠PBD = 180°. ‎ 又∠APB +∠PBA +∠PAB = 180°, ‎ ‎∴ ∠APB =∠PAC +∠PBD . ‎ ‎（2）不成立. ‎ 图4‎ ‎（3）(a)当动点P在射线BA的右侧时，结论是 ‎∠PBD=∠PAC+∠APB .‎ ‎(b)当动点P在射线BA上，‎ 结论是∠PBD =∠PAC +∠APB .‎ 或∠PAC =∠PBD +∠APB 或 ∠APB = 0°，‎ ‎∠PAC =∠PBD（任写一个即可）.‎ ‎(c) 当动点P在射线BA的左侧时，‎ 图5‎ 结论是∠PAC =∠APB +∠PBD . ‎ 选择(a) 证明：‎ 如图4，连接PA，连接PB交AC于M ‎ ∵ AC∥BD ,‎ ‎∴ ∠PMC =∠PBD .‎ 又∵∠PMC =∠PAM +∠APM ,‎ ‎∴ ∠PBD =∠PAC +∠APB . ‎ 选择(b) 证明：如图5 ‎ 图6‎ ‎∵ 点P在射线BA上，∴∠APB = 0°.‎ ‎∵ AC∥BD , ∴∠PBD =∠PAC . ‎ ‎∴ ∠PBD =∠PAC +∠APB ‎ 或∠PAC =∠PBD+∠APB ‎ 或∠APB = 0°，∠PAC =∠PBD. ‎ 选择(c) 证明：‎ 如图6，连接PA，连接PB交AC于F ‎∵ AC∥BD , ∴∠PFA =∠PBD .‎ ‎∵ ∠PAC =∠APF +∠PFA , ‎ ‎∴ ∠PAC =∠APB +∠PBD 总结：这类题主要考查平行线的性质，三角形的内角和，外角性质及其应用，在求解角的度数时，一般运用三角形的角及外角的关系，把所求的角集中在同一个三角形中，然后利用内角和求角度，在证明角之间的关系时，常考虑利用三角形的内角和定理和外角性质，若题中没有三角形，常通过作辅助线构造三角形。‎ ‎（三）利用四边形的相关知识证明角的有关问题 例6 已知：如图，在△ABC中，AB＝AC，E是AB的中点，以点E为圆心，EB为半径画弧，交BC于点D，连结ED，并延长ED到点F，使，连结FC．求证：∠F＝∠A．‎ 分析：要证明∠F＝∠A，由图知只要证明四边形AEFC是平行四边形即可。‎ 证明：∵AB=AC ‎∴∠ABC=∠ACB ‎∵EB=ED ‎∴∠EBD=∠EDB ‎ ∴∠EDB=∠ACB ‎ ∴EF∥AC E是AB的中点 ‎ ∴AE=EB ‎ ∵DF＝DE，EB=ED ‎ ∴AE=EB= DF＝DE ‎∴AE+EB= DF+DE 即AB=EF ‎∵AB=AC ‎∴EF=AC 又∵EF∥AC ‎∴四边形AEFC是平行四边形 ‎∴∠F＝∠A 说明：本例的证明用到了等腰三角形的两底角相等，平行四边形的对角相等。‎ ‎（四）利用圆的相关知识 例7如图，已知BC是直径，，AD⊥BC.‎ 求证：（1）∠EAF=∠AFE ‎ （2）BE=AE=EF 分析：由BC是直径，得到∠BAC是直角，再利用，‎ ‎ 得到∠ABE=∠BAE；再证∠EAF=∠FAE。‎ 证明：（1）∵BC是直径 ‎∴∠BAC=90 o ‎∴∠ABE+∠EFA=90 o ，∠BAE+∠EAF=90 o ‎∵‎ ‎∴∠ABE=∠BAE ‎∴∠EAF=∠AFE ‎ （2）略 说明：本例的证明用到了等弧所对的圆周角相等，等角的余角相等 例8 已知：如图，AD为锐角△ABC外接圆的直径，AE⊥BC于E，交⊙O于F。‎ ‎ 求证：∠1=∠2‎ 分析：∠1和∠2分别是和所对的两个圆周角，故只需证=，但不易证明，由于∠2+∠C=90 o ，联想到把∠1放到直角三角形中，连结BD，可得∠ABD=90 o，从而问题得证。‎ 证明：连结BD ‎∵AD为直径 ‎∴∠ABD=90 o ‎∴∠1+∠D=90 o ‎∵AE⊥BC于E ‎∴∠2+∠C=90 o ‎∵∠C=∠D ‎∴∠1=∠2‎ 总结：此题关键是见直径构造90 o的圆周角 例9　已知：如图，AB为⊙O的直径，AC为弦，CD⊥AB于D，若AE＝AC，BE交⊙O于点F，连结EF、DE．‎ ‎　　求证：（1）AE2＝AD·AB；‎ ‎　　（2）∠ACF＝∠AED．‎ 分析：（1）因为AE=AC，要证AE2＝AD·AB，实际上证AC2＝AD·AB，可转化成比例式，放入三角形中用相似三角形来证明。‎ ‎（2）欲证∠ACF＝∠AED，又知∠ACF＝∠ABE，则只需证∠AED=∠ABE，由（1）得 ‎△ADE∽△AEB，对应角相等得证 证明：（1）连结BC．‎ ‎　　∵AB是⊙O的直径，∴∠ACB＝90°．‎ ‎　　又∵CD⊥AB于D，∴∠ADC＝90°．‎ ‎　　而∠CAB＝∠DAC，∴△CAB∽△DAC．‎ ‎　　∴，∴AC2＝AD·AB．‎ ‎　　又AE＝AC，∴AE2＝AD·AB．‎ ‎　　（2）由（1），AE2＝AD·AB，∴．‎ ‎　　在△AED和△ABE中，∠EAB＝∠DAE，‎ ‎　　∴△EAB∽△DAE．∴∠ABE＝∠AED．‎ 而∠ABE＝∠ACF，‎ ‎∴∠ACF＝∠AED．‎ 总结：圆周角定理可提供等角、直角等结论，进而可用于相似三角形判定，从而可得比例式，求线段长等结论，解决此类问题是灵活选用圆周角定理和相似等内容，并适时添加辅助线。‎ ‎（五）利用三角函数求两角之间的关系 例10 已知抛物线的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C（0，3），过点C作x轴的平行线与抛物线交于点D，抛物线的顶点为M，直线y= x+5经过D、M两点.‎ ‎（1）求此抛物线的解析式；‎ ‎（2）连接AM、AC、BC，试比较∠MAB和∠ACB的大小，并说明你的理由.‎ 解：（1）∵CD∥x轴且点C（0，3），‎ ‎∴设点D的坐标为(x，3) ．‎ ‎∵直线y= x+5经过D点，‎ ‎∴3= x+5．∴x=－2．‎ 即点D(－2，3) ．‎ 根据抛物线的对称性，设顶点的坐标为M（－1，y），‎ 又∵直线y= x+5经过M点，‎ ‎∴y =－1+5，y =4．即M（－1，4）．‎ ‎∴设抛物线的解析式为．‎ ‎∵点C（0，3）在抛物线上，∴a=－1．‎ 即抛物线的解析式为． ‎ ‎（2）作BP⊥AC于点P，MN⊥AB于点N．‎ 由（1）中抛物线可得 点A（－3，0），B（1，0），‎ ‎∴AB=4，AO=CO=3，AC=．‎ ‎∴∠PAB＝45°．‎ ‎∵∠ABP=45°，∴PA=PB=．‎ ‎∴PC=AC－PA=．‎ 在Rt△BPC中，tan∠BCP==2．‎ 在Rt△ANM中，∵M（-1，4），∴MN=4．∴AN=2．‎ tan∠NAM==2．‎ ‎∴∠BCP＝∠NAM．‎ 即∠ACB＝∠MAB ‎ 说明：本例第二问判断∠ACB和∠MAB的大小关系是通过构造直角三角形，通过计算这两个角的三角函数值来解决问题的。在解决这类问题时如果不能用全等等方法来寻找思路时，不妨从直角三角形入手，分别计算所求角的三角函数值，从而使问题得到解决.同时还要注意通过一些特殊的点，可能构成特殊的三角形。‎ ‎【智能巧练】‎ ‎⒈如图，△ABC中，∠B的平分线与∠ACB的外角平分线相交于点D，则∠D与 ‎∠A的比是________‎ ‎ ‎ ‎⒉.已知，如图，在△ABC中，AC2=AD AB。‎ 求证：∠ACD=∠ABC。 ‎ ‎⒊ 如图，已知：平行四边形ABCD中，E是CA延长线上的点，‎ F是AC延长线上的点，且AE=CF 求证：⑴∠E=∠F；‎ ‎⑵BE=DF ‎⒋ 如图，△ABC中，高BD、CE交于点F，且CG=AB，BF=AC，连接AF， ‎ 求证：AG⊥AF ‎ ‎ ‎ 第4题 第5题 ‎ ‎⒌ Rt△ABC中，∠A=90°，AB=AC，D为BC上任意一点，DF⊥AB，DE⊥AC，垂足分别为F、E，M为BC中点，试判断△MEF是什么形状的三角形，并说明之.‎ ‎6．已知：如图，AD是△ABC外角∠EAC的平分线，交BC的延长线于点D. 延长DA交△‎ ABC的外接圆于点F.‎ ‎ ⑴求证：∠FBC=∠FCB；‎ ‎⑵若，求FB的长.‎ B C D E A F ‎ ‎ ‎ 第7题 第8题 ‎7．梯形ABCD中AB//CD，对角线AC、BD垂直相交于H，M是AD上的点，MH所 在直线交BC于N. 在以上前提下，试将下列设定中的两个作为题设，另一个作为结论 组成一个正确的命题，并证明这个命题. ①AD=BC ②MN⊥BC ③AM=DM ‎8．⑴如图，已知直线AB过圆心O，交⊙O于A、B，直线AF交⊙O于F（不与B重 合），直线l交⊙O于C、D，交AB于E，且与AF垂直，垂足为G，连结AC、AD．‎ 求证：①∠BAD＝∠CAG；②AC·AD＝AE·AF．‎ ‎⑵在问题⑴中，直线l向下平行移动，与⊙O相切，其他条件不变．‎ ‎①请你画出变化后的图形，并对照图，标记字母；‎ ‎②问题⑴中的两个结论是否仍成立？如果成立，请给出证明；如果不成立，请说明理由．‎ B O A 图（2）‎ ‎·‎ 图(1)‎ B O A F D C G E l ‎·‎ ‎9．如图，⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D，DF⊥AC，垂足为F，DE⊥BC，垂足为E，给出下列4个结论：‎ ‎①CE=CF；②∠ACB=∠EDF；③DE是⊙O的切线；④=；‎ 其中一定成立的是（ ）‎ A. ①②③ B. ②③④ C. ①③④ D . ①②④‎ ‎ ‎ ‎10．已知，如图，在四边形ABCD中，AB=DC，E、F分别为BC、AD的中点，BA、CD的延长线分别与EF的延长线交于H、G.‎ 求证：∠BHE=∠CGE ‎11．已知：AB是⊙O的直径，弦CD⊥AB于M，点E是上一动点.‎ ‎⑴ 如图1，若DE交AB于N，交AC于F，且DE=AC，连结AD、CE，‎ 求证：①∠CED=∠ADE ②=NF·NE ‎⑵ 如图2，若DE与AC的延长线交于F，且DE=AC，那么=NF·NE的结论是否成立？若成立请证明，若不成立请说明理由.‎ ‎ ‎ 图1 图2‎ ‎【答案点击】‎ ‎⒈ 1∶2； ⒉证明△ACD∽△ABC； ⒊证明△ABE≌△CDF，或连结ED、FB，证明平行四边形EBFD； ⒋证明△CAG≌△BFA，∴∠G=∠BAF，∵∠G+∠GAE=90°，∴∠BAF+∠GAE=90°，∴AG⊥AF； ⒌△MEF是等腰Rt△，连结AM，证△AME≌△BMF 6、⑴∵∠DAC=∠FBC，∠EAD=∠FAB=∠FCB，∵∠DAC =∠EAD，∴∠FBC=∠FCB ⑵证明△FBA∽△FDB，得FB=6 7、题设①② 结论③ 证明略8、⑴①略，②连结DF，可证得△ACE∽△AFD，⑵结论仍成立.‎ ‎9、分析 ①可证得△CDF≌△CDE，得CE=CF成立；‎ ‎②∠ACB和∠EDF（无直接关系，找相关的角）：∠ACB与∠ACE邻角互补，∠EDF也和∠ACE互补(四边形的内角和360°)，同角的补角相等，即∠ACB=∠EDF；‎ ‎④所对的圆周角为∠DCA，所对的圆周角为∠DAB，∵∠DAB=∠DCE（四边形的外角等于不相邻的内角），又∠DCA=∠DCE ，∴∠DCA=∠DCE，‎ ‎=，故选D. ‎ 一般的，证明线段相等或角相等，可根据条件寻找三角形，证三角形全等；无三角形全等时，可找与之相关连的线段或角，探索等量关系；证明弧相等，可以转化为证明弧所对的圆周角或圆心角相等，即转化为证明角相等的问题.‎ ‎10、提示:‎ 连结BD，取BD的中点M，连结FM、EM.只需证FM=EM，即可证得∠BHE=∠CGE.‎ ‎11、⑴证明：①∵DE=AC，‎ ‎∴，‎ ‎∴∠CED=∠ADE ‎②连结CN ‎∴CN=DN， ∠NCF=∠ADE（圆的轴对称性质）‎ ‎∵∠CED=∠ADE，∠CNF=∠ENC ‎∴△NCE∽△NFC ‎∴，‎ ‎∴=NF·NE ‎【自主检测】‎ ‎1．已知如左图，在ABC中, ∠BAC=90°， AB=AC,M为AC的中点，AD⊥BM。‎ 求证:∠AMB=∠DMC ‎ ‎ ‎ 2. 如右图在△ABC中，EF⊥AB，CD⊥AB，G在AC边上并且∠GDC=∠EFB，‎ 求证：∠AGD=∠ACB ‎ ‎ ‎3、如图，在△ABC中，∠B=90，点G、E在BC边上，且AB=BG=GE=GC。‎ 求证:∠AGB=∠AEB+∠ACB ‎ ‎ ‎4、如图，△ABC內接于圆，D是弧BC的中点，AD交BC于E，‎ 求证：∠ABD=∠AEC ‎ ‎5、已知：AB是⊙O的直径，C是⊙O上一点，连接AC，过点C作直线CD⊥AB 于点D，E是AB上一点，直线CE与⊙O交于点F，连结AF，与直线CD交于点G.‎ 求证：∠ACD=∠F.‎ 答案：‎ ‎1、过点C作CF⊥AC交AD的延长线于F. ‎ 证明：△ABM≌△ACF，再证△MCD≌△FCD ‎2、分析：CD∥EF ∵EF⊥AB，CD⊥AB ∴CD∥EF ‎∴∠DCB=∠EFB ∵∠GDC=∠EFB∴∠DCB=∠GDC ‎∴GD∥CB∴∠AGD=∠ACB ‎ ‎3、分析 先证明△AGE∽△CGA，再利用外角性质 ‎4、分析 要证明两个角相等，‎ 可放入两三角形△ABD、△AEC，证三角形相似，‎ 条件有两个：∠D=∠C，∠BAD=∠CAD（等弧所对的圆周角相等）‎ 证明：∵D是弧BC的中点，‎ ‎∴∠BAD=∠CAD ‎∵∠D=∠C，∴△ABD∽△AEC ‎ ‎ ∴∠ABD=∠CEA ‎5、分析 要证明∠ACD=∠F，可通过角之间的转化，‎ 已知中AB是⊙O的直径是关键的条件，‎ 连结BC，得∠ACB=90°，∠ACD=∠B（直角三角形母子三角形中的对应角相等），‎ ‎∠F=∠B，（同弧所对的圆周角相等）.‎ 证明：⑴连结BC，∵AB是⊙O的直径，‎ ‎∴∠ACB=90°（直径所对的圆周角为直角），‎ 即∠ACD+∠DCB=90°‎ ‎∵CD⊥AB ∴∠DCB+∠B=90°，∴∠ACD=∠B（同角的余角相等）‎ ‎∵∠F=∠B，∴∠ACD=∠F（等量代换）.‎ 证明角相等时，如果没有三角形全等，我们常找与它们都相关或都有联系的角作为桥梁，实现角之间的转化，从而证明它们的等量关系. 直角三角形的母子三角形中相等的角、成比例的线段要熟悉.‎