中考数学复习教案时图形的初步认识 6页

中考数学复习教案 第17课时 图形的初步认识 一、知识点 ‎ 1．立体图形：视图，平面展开图；‎ ‎ 2．平面图形：点和线，两点之间线段最短。‎ ‎ （1）角：对顶角相等，等角的补角相等，等角的余角相等；‎ ‎ （2）平行线：两位角相等，两直线平行；两直线平行，同位角相等。‎ 二、中考课标要求 考点 课标要求 知识与技能目标 了解 理解 掌握 灵活应用 视图 三视图的宝义 ‎∨‎ 由立体图形到视图 ‎∨‎ ‎∨‎ 由视图到立体图形 ‎∨‎ 平面展开 由多面体求平面展开图 ‎∨‎ ‎∨‎ 由平面展开图判断多面体 ‎∨‎ ‎∨‎ 平面图形 多边形的定义 ‎∨‎ ‎∨‎ 多边形的分割 ‎∨‎ ‎∨‎ 线段 线段的定义、中点 ‎∨‎ ‎∨‎ 线段的比较、度量 ‎∨‎ 线段公理 ‎∨‎ ‎∨‎ 直线 直线公理，垂线性质 ‎∨‎ 对顶角的性质 ‎∨‎ 平行线的性质、判定 ‎∨‎ ‎∨‎ 射线 角的和、差，角平分线 ‎∨‎ ‎∨‎ 角的比较、度量 ‎∨‎ ‎∨‎ 互余、互补性质 ‎∨‎ ‎∨‎ 三、中考知识梳理 ‎ 1.立体图形的展开图 ‎ 这类问题，主要考查对立体图形与平面图形的关系的认识，因此要求掌握常用多面体的平面展开图的识别及逆向判断。‎ ‎ 2.角的有关计算 ‎ 这类问题一般主要考查互余、互补、对顶角的性质及平行线的性质的运用，首先根据已知条件观察图形，分析角与角之间的数量关系，从中找到解决问题的思路及途径，在中考中通常和三角形的内角和定理，内外角性质，或特殊三角形相联系。‎ ‎ 3.平行线的性质与判定的运用 ‎ 平行线的特征与识别是互逆的，有时易混淆，在中考中往往综合运用，也经常与后续知识，平行四边形、相似形等相联系，是中考的重点之一。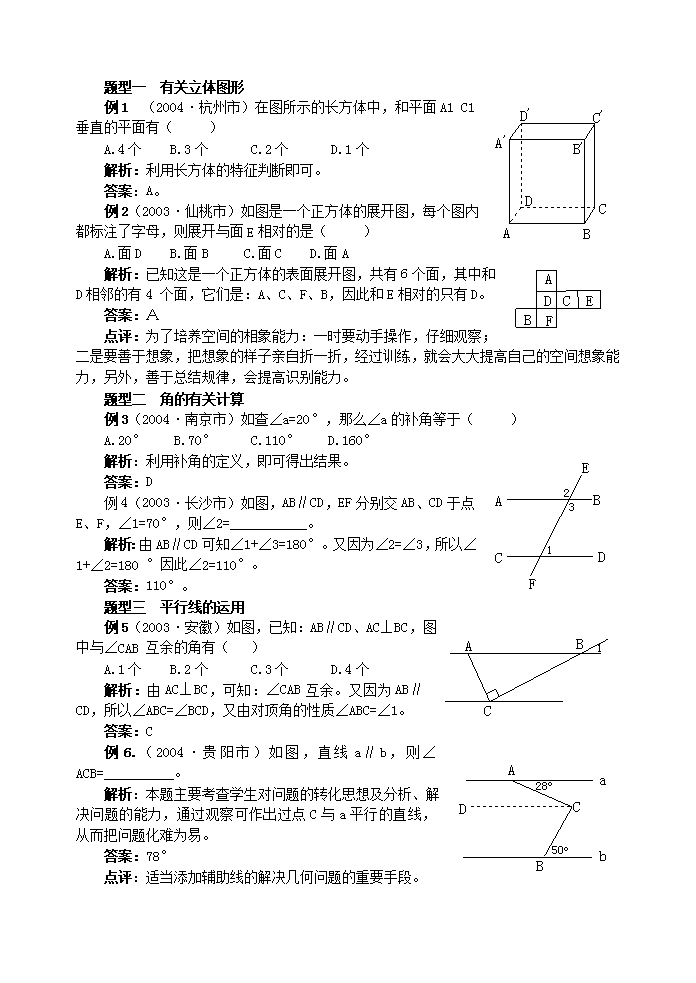‎ 四、中考题型例析 ‎ 题型一 有关立体图形 ‎ ‎ 例1 （2004·杭州市）在图所示的长方体中，和平面A‎1 C1 垂直的平面有（ ）‎ ‎ A.4个 B.3个 C.2个 D.1个 ‎ 解析：利用长方体的特征判断即可。‎ ‎ 答案：A。‎ ‎ 例2（2003·仙桃市）如图是一个正方体的展开图，每个图内都标注了字母，则展开与面E相对的是（ ）‎ ‎ A.面D B.面B C.面C D.面A ‎ 解析：已知这是一个正方体的表面展开图，共有6个面，其中和D相邻的有4 个面，它们是：A、C、F、B，因此和E相对的只有D。‎ ‎ 答案：Ａ ‎ 点评：为了培养空间的相象能力：一时要动手操作，仔细观察；二是要善于想象，把想象的样子亲自折一折，经过训练，就会大大提高自己的空间想象能力，另外，善于总结规律，会提高识别能力。‎ ‎ 题型二 角的有关计算 ‎ 例3（2004·南京市）如查∠a=20°，那么∠a的补角等于（ ）‎ ‎ A.20° B.70° C.110° D.160°‎ ‎ 解析：利用补角的定义，即可得出结果。‎ ‎ 答案：D ‎ 例4（2003·长沙市）如图，AB∥CD，EF分别交AB、CD于点E、F，∠1=70°，则∠2=___________。‎ ‎ 解析：由AB∥CD可知∠1+∠3=180°。又因为∠2=∠3，所以∠1+∠2=180 °因此∠2=110°。‎ ‎ 答案：110°。‎ ‎ 题型三 平行线的运用 ‎ 例5（2003·安徽）如图，已知：AB∥CD、AC⊥BC，图中与∠CAB 互余的角有（ ）‎ ‎ A.1个 B.2个 C.3个 D.4个 ‎ 解析：由AC⊥BC，可知：∠CAB互余。又因为AB∥CD，所以∠ABC=∠BCD，又由对顶角的性质∠ABC=∠1。‎ ‎ 答案：C ‎ 例6.（2004·贵阳市）如图，直线a∥b，则∠ACB=__________。‎ ‎ 解析：本题主要考查学生对问题的转化思想及分析、解决问题的能力，通过观察可作出过点C与a平行的直线，从而把问题化难为易。‎ ‎ 答案：78°‎ ‎ 点评：适当添加辅助线的解决几何问题的重要手段。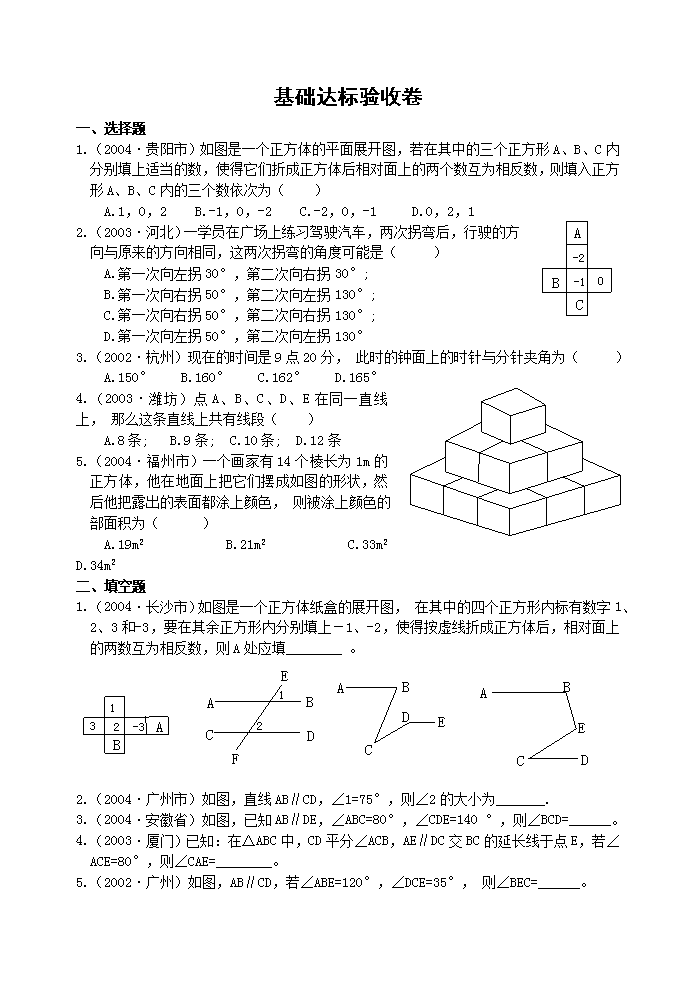‎ 基础达标验收卷 一、选择题 ‎1.（2004·贵阳市）如图是一个正方体的平面展开图， 若在其中的三个正方形A、B、C内分别填上适当的数， 使得它们折成正方体后相对面上的两个数互为相反数，则填入正方形A、B、C内的三个数依次为（ ）‎ ‎ A.1，0，2 B.-1，0，‎-2 C.-2，0，-1 D.0，2，1‎ ‎2.（2003·河北）一学员在广场上练习驾驶汽车，两次拐弯后，行驶的方向与原来的方向相同，这两次拐弯的角度可能是（ ）‎ ‎ A.第一次向左拐30°，第二次向右拐30°;‎ ‎ B.第一次向右拐50°，第二次向左拐130°;‎ C.第一次向右拐50°，第二次向右拐130°;‎ D.第一次向左拐50°，第二次向左拐130°‎ ‎3.（2002·杭州）现在的时间是9点20分， 此时的钟面上的时针与分针夹角为（ ）‎ ‎ A.150° B.160° C.162° D.165°‎ ‎4.（2003·潍坊）点A、B、C、D、E在同一直线上， 那么这条直线上共有线段（ ）‎ ‎ A.8条; B.9条; C.10条; D.12条 ‎5.（2004·福州市）一个画家有14个棱长为‎1m的正方体，他在地面上把它们摆成如图的形状，然后他把露出的表面都涂上颜色， 则被涂上颜色的部面积为（ ）‎ ‎ A‎.19m2‎ B‎.21m‎2‎ C.33m2‎ D‎.34m2‎ 二、填空题 ‎1.（2004·长沙市）如图是一个正方体纸盒的展开图， 在其中的四个正方形内标有数字1、2、3和-3，要在其余正方形内分别填上－1、-2，使得按虚线折成正方体后，相对面上的两数互为相反数，则A处应填________ 。‎ ‎2.（2004·广州市）如图，直线AB∥CD，∠1=75°，则∠2的大小为_______. ‎ ‎3.（2004·安徽省）如图，已知AB∥DE，∠ABC=80°，∠CDE=140 °，则∠BCD=______。‎ ‎4.（2003·厦门）已知：在△ABC中，CD平分∠ACB，AE∥DC交BC的延长线于点E，若∠ACE=80°，则∠CAE=________。‎ ‎5.（2002·广州）如图，AB∥CD，若∠ABE=120°，∠DCE=35°， 则∠BEC=______。‎ 三、解答题 ‎1.（2003·嘉兴市）每一个多边形都可以按图的方法分割成若干个三角形，（1）请根据图示方法把七边形分割成若干个三角形，（2）按图示方法，十二边形可以分割成几个三角形图‎1-3-12‎（只要求写出答案）。‎ ‎2.（希望杯“邀请赛试题）如图，OM∠AOB的平分线，射线OC在∠BOM内部，ON是∠BOC的平分线，已知∠AOC=80°，求∠MON的度数。‎ ‎3.（天津市竞赛题）如图，在△ABC中，CE⊥AB于E，DF⊥AB于F，AC ∥ED，CE是∠ACB的平分线，求证：∠EDF=∠BDF。‎ ‎4.（武汉市竞赛题）如图‎1-3-15‎，已知AB∥CD，∠EAF=∠EAB，∠ECF=∠ECD。‎ 求证：∠AFC=∠AEC。‎ 能力提高练习 ‎1.如图，在∠AOE的内部，从O引出四条射线OB，OC，OD，OF，图中共有多少个小于平角的角？‎ ‎2.一条直线上有...，等n个点，问：‎ ‎ （1）这条直线上共有多少条射线？‎ ‎ （2）这条直线上共有多少条线段？‎ ‎3.如图‎1-3-17‎，AB∥CD，分别探讨下面四个图形中，∠APC与∠PAB、∠PCD 之间有什么关系？请你从所得的四个关系中任选一个加以证明。‎ ‎4.平面内有若干条直线，当下列情形时，可将平面最多分成几部分。‎ ‎ （1）有一条直线时，最多可分为_______部分。‎ ‎ （2）有两条直线时，最多可分为________部分。‎ ‎ （3）有三条直线时，最多可分为________部分。‎ ‎ （4）有n条直线时，最多可分为_______________部分。‎ 答案：‎ 基础达标验收卷 一、1.A 2.A 3.B 4.C 5.C 二、1.-2 2.105° 3.40° 4.50° 5.95°‎ 三、‎ ‎1.(1)略 (2)10个 ‎2.解:∠MON=∠AOB-∠BOC=(∠AOB-∠BOC)=∠AOC=×80°=40°.‎ ‎3.证明:∵CE∥DF,∴∠EDF=∠DEC.‎ ‎ 又∵AC∥DE,∴∠DEC=∠ACE.‎ ‎ ∴∠ACE=∠EDF.‎ ‎ 又∵DF∥CE,∴∠FDB=∠ECB.‎ ‎ 又∵∠ACE=∠ECB,‎ ‎ ∴∠EDF=∠FBD.‎ ‎4.提示:∠AEC=∠EAB+∠ECD.‎ ‎ ∠AFC=∠FAB+∠FCD.‎ ‎ ∠AEC=∠FAB+∠FCD+∠EAF+∠ECF.‎ 能力提高练习 ‎1.15个角 2.(1)2n (2)‎ ‎3.(1)∠APC=360°-∠PAB-∠PCD.‎ ‎ (2)∠APC=∠PAB+∠PCD.‎ ‎ (3)∠APC=∠PCD-∠PAB.‎ ‎ (4)∠APC=∠PAB-∠PCD.‎ ‎ 证明略 ‎4.(1)2 (2)4 (3)7 (4).‎