2020年河北省中考数学真题试卷（含答案） 25页

2020 年河北省中考数学真题试卷（含答案） 一、选择题（本大题有 16 个小题，共 42 分.1~10 小题各 3 分，11~16 小题各 2 分．在每小题 给出的四个选项中，只有一项是符合题目要求的） 1.如图，在平面内作已知直线 m 的垂线，可作垂线的条数有（ ） A. 0 条 B. 1 条 C. 2 条 D. 无数条 【答案】D 【解析】 【分析】 在同一平面内，过已知直线上的一点有且只有一条直线垂直于已知直线；但画已知直线的垂线，可以画无 数条． 【详解】在同一平面内，画已知直线的垂线，可以画无数条； 故选：D． 【点睛】此题主要考查在同一平面内，垂直于平行的特征，解题的关键是熟知垂直的定义． 2.墨迹覆盖了等式“ 3x 2xx （ 0x  ）”中的运算符号，则覆盖的是（ ） A. ＋ B. － C. × D. ÷ 【答案】D 【解析】 【分析】 直接利用同底数幂的除法运算法则计算得出答案． 【详解】∵ 3x 2xx （ 0x  ）， 32xxx ， ∴覆盖的是：÷． 故选：D． 【点睛】本题主要考查了同底数幂的除法运算，正确掌握相关运算法则是解题关键． 3.对于① 3(13 )xxyxy ，② 2( 3)( 1) 2 3x x x x     ，从左到右的变形，表述正确的是（ ） A. 都是因式分解 B. 都是乘法运算 C. ①是因式分解，②是乘法运算 D. 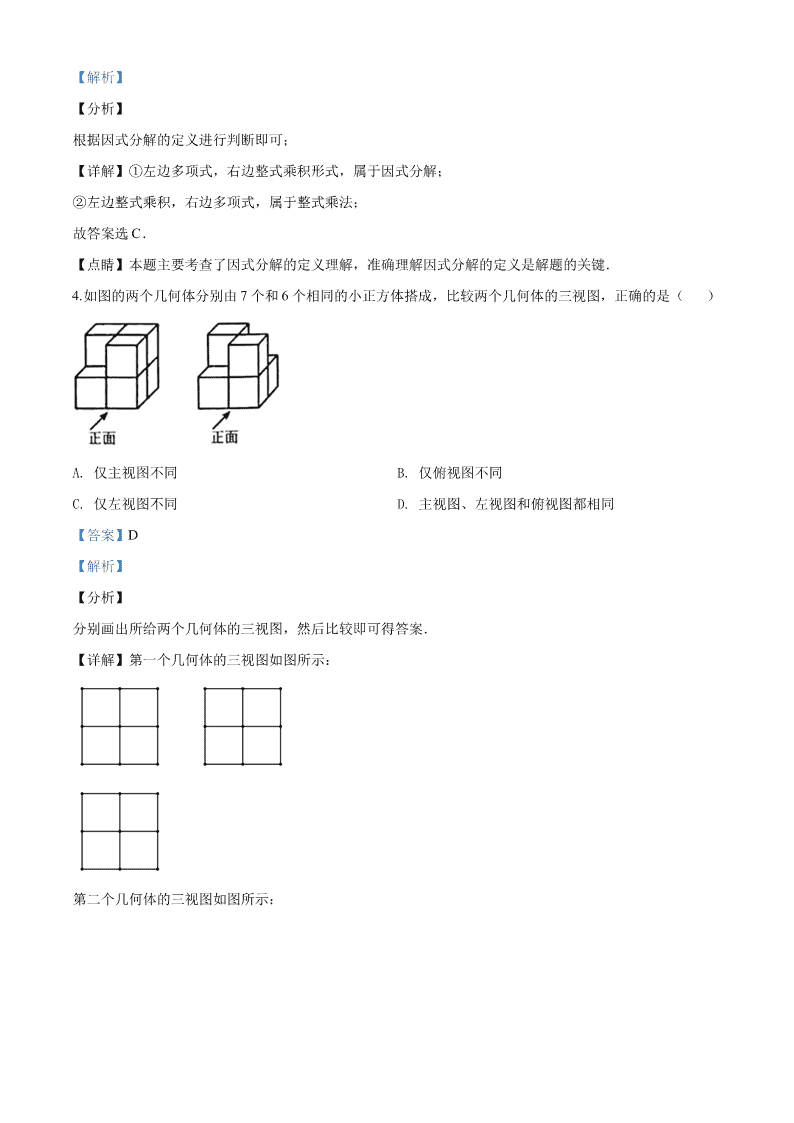①是乘法运算，②是因式分解 【答案】C 【解析】 【分析】 根据因式分解的定义进行判断即可； 【详解】①左边多项式，右边整式乘积形式，属于因式分解； ②左边整式乘积，右边多项式，属于整式乘法； 故答案选 C． 【点睛】本题主要考查了因式分解的定义理解，准确理解因式分解的定义是解题的关键． 4.如图的两个几何体分别由 7 个和 6 个相同的小正方体搭成，比较两个几何体的三视图，正确的是（ ） A. 仅主视图不同 B. 仅俯视图不同 C. 仅左视图不同 D. 主视图、左视图和俯视图都相同 【答案】D 【解析】 【分析】 分别画出所给两个几何体的三视图，然后比较即可得答案． 【详解】第一个几何体的三视图如图所示： 第二个几何体的三视图如图所示： 观察可知这两个几何体的主视图、左视图和俯视图都相同， 故选 D． 【点睛】本题考查了几何体的三视图，正确得出各几何体的三视图是解题的关键． 5.如图是小颖前三次购买苹果单价的统计图，第四次又买的苹果单价是 a 元/千克，发现这四个单价的中位 数恰好也是众数，则 a  （ ） A. 9 B. 8 C. 7 D. 6 【答案】B 【解析】 【分析】 根据统计图中的数据结合中位数和众数的定义，确定 a 的值即可． 【详解】解：由条形统计图可知，前三次的中位数是 8 ∵第四次又买的苹果单价是 a 元/千克，这四个单价的中位数恰好也是众数 ∴a=8． 故答案为 B． 【点睛】本题考查条形统计图、中位数和众数的定义，掌握中位数和众数的定义是解答本题的关键． 6.如图 1，已知 ABC ，用尺规作它的角平分线． 如图 2，步骤如下， 第一步：以 B 为圆心，以 为半径画弧，分别交射线 BA ， BC 于点 D ， E ； 第二步：分别以 ， 为圆心，以b 为半径画弧，两弧在 内部交于点 P ； 第三步：画射线 BP ．射线 即为所求． 下列正确的是（ ） A. a ， b 均无限制 B. 0a  ， 1 2b D E 的长 C. 有最小限制， 无限制 D. 0a  ， 1 2b D E 的长 【答案】B 【解析】 【分析】 根据作角平分线的方法进行判断，即可得出结论． 【详解】第一步：以 B 为圆心，适当长为半径画弧，分别交射线 BA ， BC 于点 D ， E ； ∴ 0a  ； 第二步：分别以 ， 为圆心，大于 1 2 DE 的长为半径画弧，两弧在 ABC 内部交于点 P ； ∴ 1 2bDE 的长； 第三步：画射线 ．射线 即为所求． 综上，答案为： ； 的长， 故选：B． 【点睛】本题主要考查了基本作图，解决问题的关键是掌握作角平分线的方法． 7.若 ab¹ ，则下列分式化简正确的是（ ） A. 2 2 aa bb   B. 2 2 aa bb   C. 2 2 aa bb D. 1 2 1 2 a a bb  【答案】D 【解析】 【分析】 根据 a≠b，可以判断各个选项中的式子是否正确，从而可以解答本题． 【详解】∵a≠b， ∴ 2 2 aa bb   ，选项 A 错误； 2 2 aa bb   ，选项 B 错误； 2 2 aa bb ，选项 C 错误； 1 2 1 2 a a bb  ，选项 D 正确； 故选：D． 【点睛】本题考查分式的混合运算，解答本题的关键是明确分式混合运算的计算方法． 8.在如图所示的网格中，以点 O 为位似中心，四边形 A B C D 的位似图形是（ ） A. 四边形 N P M Q B. 四边形 N P M R C. 四边形 NHMQ D. 四边形 N H M R 【答案】A 【解析】 【分析】 以 O 为位似中心，作四边形 ABCD 的位似图形，根据图像可判断出答案． 【详解】解：如图所示，四边形 的位似图形是四边形 ． 故选：A 【点睛】此题考查了位似图形的作法，画位似图形的一般步骤为：①确定位似中心；②分别连接并延长位 似中心和能代表原图的关键点；③根据相似比，确定能代表所作的位似图形的关键点；顺次连接上述各点， 确定位似图形． 9.若    2291111 81012k   ，则 k  （ ） A. 12 B. 10 C. 8 D. 6 【答案】B 【解析】 【分析】 利用平方差公式变形即可求解． 【详解】原等式 变形得：   2291111 81012k        9 1 9 1 11 1 11 1 8 10 12      8101012 81012   10 ． 故选：B． 【点睛】本题考查了平方差公式的应用，灵活运用平方差公式是解题的关键． 10.如图，将 ABC 绕边 AC 的中点O 顺时针旋转 180°．嘉淇发现，旋转后的 CDA 与 构成平行 四边形，并推理如下： 点 A ， C 分别转到了点 ， 处， 而点 B 转到了点 D 处． ∵ C B A D ， ∴四边形 A B C D 是平行四边形． 小明为保证嘉淇的推理更严谨，想在方框中“∵ ，”和“∴四边形……”之间作补充．下列正确 的是（ ） A. 嘉淇推理严谨，不必补充 B. 应补充：且 A B C D ， C . 应补充：且 //A B C D D. 应补充：且 OAOC ， 【答案】B 【解析】 【分析】 根据平行四边形的判定方法“两组对边分别相等的四边形是平行四边形”即可作答． 【详解】根据旋转的性质得： CB=AD，AB=CD， ∴四边形 ABDC 是平行四边形； 故应补充“AB=CD”， 故选：B． 【点睛】本题主要考查了平行四边形的判定和旋转的性质，牢记旋转前、后的图形全等，熟练掌握平行四 边形的判定方法是解题的关键． 11.若 k 为正整数，则()k kk k k k    个 （ ） A. 2kk B. 21kk  C. 2 kk D. 2 kk  【答案】A 【解析】 【分析】 根据乘方的定义及幂的运算法则即可求解． 【详解】 ()k kk kkk  个    2 kkk k k = 2 kk ， 故选 A． 【点睛】此题主要考查幂的运算，解题的关键是熟知其运算法则． 12.如图，从笔直的公路 l 旁一点 P 出发，向西走 6 k m 到达 ；从 出发向北走 也到达 ．下列说法错． 误．的是（ ） A. 从点 向北偏西 45°走 3 k m 到达 B. 公路 的 走向是南偏西 45° C. 公路 走向是北偏东 45° D. 从点 向北走 后，再向西走 到达 【答案】A 【解析】 【分析】 根据方位角的定义及勾股定理逐个分析即可． 【详解】解：如图所示，过 P 点作 AB 的垂线 PH， 选项 A：∵BP=AP=6km，且∠BPA=90°，∴△PAB 为等腰直角三角形，∠PAB=∠PBA=45°， 又 PH⊥AB，∴△PAH 为等腰直角三角形， ∴PH= 2 322 PA km，故选项 A 错误； 选项 B：站在公路上向西南方向看，公路 的走向是南偏西 45°，故选项 B 正确； 选项 C：站在公路上向东北方向看，公路 的走向是北偏东 45°，故选项 C 正确； 选项 D：从点 P 向北走 3 k m 后到达 BP 中点 E，此时 EH 为△ PEH 的中位线，故 EH= 1 2 AP=3，故再向西走 到达 l ，故选项 D 正确． 故选：A． 【点睛】本题考查了方位角问题及等腰直角三角形、中位线等相关知识点，方向角一般以观测者的位置为 中心，所以观测者不同，方向就正好相反，但角度不变． 13.已知光速为 300000 千米秒，光经过 t 秒（ 1 1 0 t ）传播的距离用科学记数法表示为 10 na  千米，则n 可能为（ ） A. 5 B. 6 C. 5 或 6 D. 5 或 6 或 7 【答案】C 【解析】 【分析】 科学记数法的表示形式为 a×10n 的形式，其中 1≤|a|＜10，n 为整数．确定 n 的值时，要看把原数变成 a 时， 小数点移动了多少位，n 的绝对值与小数点移动的位数相同． 【详解】解：当 t=1 时，传播的距离为 300000 千米，写成科学记数法为： 53 1 0 千米， 当 t=10 时，传播的距离为 3000000 千米，写成科学记数法为： 63 1 0 千米， ∴n 的值为 5 或 6， 故选：C． 【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为 a×10n 的形式，其中 1≤|a|＜10，n 为 整数，表示时关键要正确确定 a 的值以及 n 的值． 14.有一题目：“已知；点O 为 ABC 的外心， 130BOC ，求 A ．”嘉嘉的解答为：画 以及它 的外接圆 ，连接 OB ， OC ，如图．由 2130BOCA ，得 65A ．而淇淇说：“嘉嘉考虑的 不周全， 还应有另一个不同的值．”，下列判断正确的是（ ） A. 淇淇说的对，且 的另一个值是 115° B. 淇淇说的不对， 就得 65° C. 嘉嘉求的结果不对， 应得 50° D. 两人都不对， A 应有 3 个不同值 【答案】A 【解析】 【分析】 直接利用圆内接四边形的性质结合圆周角定理得出答案． 【详解】解：如图所示： ∵∠BOC=130°， ∴∠A=65°， ∠A 还应有另一个不同的值∠A′与∠A 互补． 故∠A′＝180°−65°＝115°． 故选：A． 【点睛】此题主要考查了三角形的外接圆，正确分类讨论是解题关键． 15.如图，现要在抛物线 (4)yxx上找点 ( , )P a b ，针对 b 的不同取值，所找点 P 的个数，三人的说法如 下， 甲：若 5b  ，则点 的个数为 0； 乙：若 4b  ，则点 的个数为 1； 丙：若 3b  ，则点 的个数为 1． 下列判断正确的是（ ） A. 乙错，丙对 B. 甲和乙都错 C. 乙对，丙错 D. 甲错，丙对 【答案】C 【解析】 【分析】 分别令 x（4-x）的值为5，4，3，得到一元二次方程后，利用根的判别式确定方程的根有几个，即可得到点P的个 数． 【详解】当 b=5 时，令 x （ 4-x ） =5，整理得：x2-4x＋5=0，△=(-4)2-4×5=-6<0，因此点P的个数为0，甲的说法正确； 当b=4时，令x（4-x）=4，整理得：x2-4x+4=0，△=(-4)2-4×4=0，因此点P有1个，乙的说法正确； 当b=3时，令x（4-x）=3，整理得：x2-4x+3=0，△=(-4)2-4×3=4>0，因此点P有2个，丙的说法不正确； 故选：C． 【点睛】本题考查二次函数与一元二次方程，解题的关键是将二次函数与直线交点个数，转化成一元二次 方程根的判别式． 16.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案．现有五种正方形纸片，面积分 别是 1，2，3，4，5，选取其中三块（可重复选取）按图的方式组成图案，使所围成的三角形是面积最大．．的 直角三角形，则选取的三块纸片的面积分别是（ ） A. 1，4，5 B. 2，3，5 C. 3，4，5 D. 2，2，4 【答案】B 【解析】 【分析】 根据勾股定理， 222abc ，则小的两个正方形的面积等于大三角形的面积，再分别进行判断，即可得到 面积最大的三角形． 【详解】解：根据题意，设三个正方形的边长分别为 a、b、c， 由勾股定理，得 ， A、∵1+4=5，则两直角边分别为：1 和 2，则面积为： 1 1 2=12  ； B、∵2+3=5，则两直角边分别为： 2 和 3 ，则面积为： 1623=22 ； C、∵3+4≠5，则不符合题意； D、∵2+2=4，则两直角边分别为： 和 ，则面积为： 1 2 2 12    ； ∵ 6 12  ， 故选：B． 【点睛】本题考查了正方形的性质，勾股定理的应用，以及三角形的面积公式，解题的关键是熟练掌握勾 股定理，以及正方形的性质进行解题． 二、填空题（本大题有 3 个小题，共 12 分.17~18 小题各 3 分；19 小题有 3 个空，每空 2 分） 17.已知： 182222 ab ，则 ab  _________． 【答案】6 【解析】 【分析】 根据二次根式的运算法则即可求解． 【详解】∵ 18 2 3 2 2 2 2    ∴a=3,b=2 ∴ 6 故答案为：6． 【点睛】此题主要考查二次根式的运算，解题的关键是熟知其运算法则． 18.正六边形的一个内角是正 n 边形一个外角的 4 倍，则 n _________． 【答案】12 【解析】 【分析】 先根据外角和定理求出正六边形的外角为 60°，进而得到其内角为 120°，再求出正 n 边形的外角为 30°，再 根据外角和定理即可求解． 【详解】解：由多边形的外角和定理可知，正六边形的外角为：360°÷6=60°， 故正六边形的内角为 180°-60°=120°， 又正六边形的一个内角是正 边形一个外角的 4 倍， ∴正 n 边形的外角为 30°， ∴正 n 边形的边数为：360°÷30°=12． 故答案为：12． 【点睛】本题考查了正多边形的外角与内角的知识，熟练掌握正多边形的内角和和外角和定理是解决此类 题目的关键． 19.如图是 8 个台阶的示意图，每个台阶的高和宽分别是 1 和 2，每个台阶凸出的角的顶点记作 mT （ m 为 1~8 的整数）．函数 ky x （ 0x  ）的图象为曲线 L ． （1）若 过点 1T ，则 k  _________； （2）若 过点 4T ，则它必定还过另一点 ，则 m  _________； （3）若曲线 使得 18~TT这些点分布在它的两侧，每侧各 4 个点，则 k 的整数值有_________个． 【答案】 (1). －16 (2). 5 (3). 7 【解析】 【分析】 （1）先确定 T1 的坐标，然后根据反比例函数 （ ）即可确定 k 的值； （2）观察发现，在反比例函数图像上的点，横纵坐标只积相等，即可确定另一点； （3）先分别求出 T1~T8 的横纵坐标积，再从小到大排列，然后让 k 位于第 4 个和第 5 个点的横纵坐标积之 间，即可确定 k 的取值范围和 k 的整数值的个数． 【详解】解：（1）由图像可知 T1（-16,1） 又∵．函数 （ ）的图象经过 T1 ∴1 16 k  ，即 k=-16； （2）由图像可知 T1（-16,1）、 T2（-14,2）、 T3（-12,3）、 T4（-10,4）、 T5（-8,5）、 T6（-6,6）、 T7（-4,7）、 T8 （-2,8） ∵ L 过点 4T ∴k=-10×4=40 观察 T1~T8,发现 T5 符合题意，即 m=5； （3）∵T1~T8 的横纵坐标积分别为：-16，-28，-36，-40,-40，-36，-28，-16 ∴要使这 8 个点为于 的两侧，k 必须满足-36＜k＜-28 ∴k 可取-29、-30、-31、-32、-33、-34、-35 共 7 个整数值． 故答案为：（1）-16；（ 2）5；（ 3）7． 【点睛】本题考查了反比例函数图像的特点，掌握反比例函数图像上的点的横纵坐标积等于 k 是解答本题 的关键． 三、解答题（本大题有 7 个小题，共 66 分．解答应写出文字说明、证明过程或演算步骤） 20.已知两个有理数：－9 和 5． （1）计算： ( 9 ) 5 2 ； （2）若再添一个负整数 m ，且－9，5 与 这三个数的平均数仍小于 ，求 的值． 【答案】（1）－2；（ 2） 1m  ． 【解析】 【分析】 （1）根据有理数的混合运算法则即可求解； （2）根据平均数的定义列出不等式即可求出 m 的取值，故可求解． 【详解】（1） = 4 22   ； （2）依题意得 (9)5 3 m ＜m 解得 m＞-2 ∴负整数 =-1． 【点睛】此题主要考查有理数、不等式及平均数，解题的关键是熟知有理数、不等式的运算法则． 21.有一电脑程序：每按一次按键，屏幕的 A 区就会自动加上 2a ，同时 B 区就会自动减去3a ，且均显示化 简后的结果．已知 ， 两区初始显示的分别是 25 和－16，如图． 如，第一次按键后， A ， B 两区分别显示： （1）从初始状态按 2 次后，分别求 ， 两区显示的结果； （2）从初始状态按 4 次后，计算 ， 两区代数式的和，请判断这个和能为负数吗？说明理由． 【答案】（1） 22 5 2 a ； 1 6 6 a ；（ 2） 24 a 1 2 a + 9－ ；和不能为负数，理由见解析． 【解析】 【分析】 （1）根据题意，每按一次按键，屏幕的 区就会自动加上 2a ， 区就会自动减去 3a ，可直接求出初始状 态按 2 次后 A，B 两区显示的结果． （2）依据题意，分别求出初始状态下按 4 次后 A，B 两区显示的代数式，再求 A，B 两区显示的代数式的 和，判断能否为负数即可． 【详解】解：（1）A 区显示结果为： 22225+a+a=25+2a ， B 区显示结果为： 163a3a=166a﹣ － － ﹣ － ； （2）初始状态按 4 次后 A 显示为： 2222225+a+a+aa254a B 显示为： 163a3a3a3a=1612a﹣ － － － － ﹣ － ∴A+B= 225+4a+(-1612a) = = 2(2a 3)－ ∵ 2(2a 3) 0－ 恒成立， ∴和不能为负数． 【点睛】本题考查了代数式运算，合并同类项，完全平方公式问题，解题关键在于理解题意，列出代数式 进行正确运算，并根据完全平方公式判断正负． 22.如图，点O 为 AB 中点，分别延长OA 到点C ，OB 到点 D ，使 OC OD ．以点 为圆心，分别以 ， OC 为半径在 CD 上方作两个半圆．点 P 为小半圆上任一点（不与点 A ， B 重合），连接 OP 并延长交大半 圆于点 E ，连接 AE ， CP ． （1）①求证： A O E P O C≌ ； ②写出∠1，∠2 和 C 三者间的数量关系，并说明理由． （2）若 22OC OA，当 最大时，直接．．指出 与小半圆的位置关系，并求此时 E O DS 扇形 （答案保留  ）． 【答案】（1）①见详解；②∠2=∠C+∠1；（ 2） 与小半圆相切， 4 3  ． 【解析】 【分析】 （1）①直接由已知即可得出 AO=PO，∠AOE=∠POC，OE=OC，即可证明； ②由（1）得△AOE≌△POC，可得∠1=∠OPC，根据三角形外角的性质可得∠2=∠C+∠OPC，即可得出答 案； （2）当 最大时，可知此时 与小半圆相切，可得 CP⊥OP，然后根据 2 2 2OC OA OP   ，可得在 Rt△POC 中，∠C=30°，∠POC=60°，可得出∠EOD，即可求出 S 扇 EOD． 【详解】（1）①在△AOE 和△POC 中 = AOPO AOEPOC OEOC     ∠ ∠ ， ∴△AOE≌△POC； ②∠2=∠C+∠1，理由如下： 由（1）得△AOE≌△POC， ∴∠1=∠OPC， 根据三角形外角的性质可得∠2=∠C+∠OPC， ∴∠2=∠C+∠1； （2）在 P 点的运动过程中，只有 CP 与小圆相切时∠C 有最大值， ∴当 最大时，可知此时 与小半圆相切， 由此可得 CP⊥OP， 又∵ 222OCOAOP ， ∴可得在 Rt△POC 中，∠C=30°，∠POC=60°， ∴∠EOD=180°-∠POC=120°， ∴S 扇 EOD= 2120 360 R = 4 3  ． 【点睛】本题考查了全等三角形的性质和判定，三角形的外角，切线的性质，扇形面积的计算，掌握知识 点灵活运用是解题关键． 23.用承重指数 W 衡量水平放置的长方体木板的最大承重量．实验室有一些同材质同长同宽而厚度不一的木 板，实验发现：木板承重指数 与木板厚度 x （厘米）的平方成正比，当 3x  时， 3W  ． （1）求 与 的函数关系式． （2）如图，选一块厚度为 6 厘米的木板，把它分割成与原来同长同宽但薄厚不同的两块板（不计分割损耗）．设 薄板的厚度为 （厘米）， Q W W厚 薄 ． ①求 Q 与 的函数关系式； ② 为何值时， 是 W薄 的 3 倍？ 【注：（1）及（2）中的①不必写 的取值范围】 【答案】（1） 21 3Wx ；（ 2）① 12 4Qx；② 2cmx  ． 【解析】 【分析】 （1）设 W=kx2，利用待定系数法即可求解； （2）①根据题意列出函数，化简即可；②根据题意列出方程故可求解． 【详解】（1）设 W=kx2, ∵ 时， ∴3=9k ∴k= 1 3 ∴ W 与 x 的函数关系式为 21 3Wx ； （2）①∵薄板的厚度为 xcm，木板的厚度为 6cm ∴厚板的厚度为（6-x）cm， ∴Q= 2211(6)41233xxx  ∴ Q 与 的函数关系式为 1 2 4Qx ； ②∵ 是 W薄 的 3 倍 ∴-4x+12=3× 21 3 x 解得 x1=2,x2=-6(不符题意，舍去) 经检验，x=2 是原方程的解， ∴x=2 时， 是 的 3 倍． 【点睛】此题主要考查函数与方程的应用，解题的关键是根据题意找到等量关系列出函数或方程求解． 24.表格中的两组对应值满足一次函数 y kx b，现画出了它的图象为直线 l ，如图．而某同学为观察 k ，b 对图象的影响，将上面函数中的 与 交换位置后得另一个一次函数，设其图象为直线 l  ． －1 0 y －2 1 （1）求直线 的解析式； （2）请在图上画出．．直线 l  （不要求列表计算），并求直线 被直线 l 和 y 轴所截线段的长； （3）设直线 ya 与直线 ， 及 轴有三个不同的交点，且其中两点关于第三点对称，直接．．写出 a 的值． 【答案】（1） ： 31yx=+；（ 2）作图见解析，所截线段长为 2 ；（ 3） 的值为 5 2 或 17 5 或 7 【解析】 【分析】 （1）根据待定系数法即可求解； （2）根据题意得到直线 ，联立两直线求出交点坐标，再根据两点间的距离公式即可求解； （3）分对称点在直线 l，直线 和 y 轴分别列式求解即可． 【详解】（1）依题意把（-1，-2）和（0,1）代入 y kx b， 得 2 1 kb b       ， 解得 3 1 k b    ， ∴直线 的解析式为 ， （2）依题意可得直线 的解析式为 3yx=+， 作函数图像如下： 令 x=0，得 y=3，故 B（0,3）， 令 31 3 yx yx    ， 解得 1 4 x y    ， ∴A（1,4）， ∴直线 被直线 和 轴所截线段的长 AB= 22(10)(43)2 ； （3）①当对称点在直线l 上时， 令 31ax=+，解得 x= 1 3 a  , 令 3ax，解得 x= 3a  , ∴2× =a-3， 解得 a=7； ②当对称点在直线 l  上时， 则 2×（a-3）= ， 解得 a= 17 5 ； ③当对称点在 y 轴上时， 则 +（ ）=0， 解得 a= 5 2 ； 综上： a 的值为 或 或 7． 【点睛】此题主要考查一次函数与几何综合，解题的关键是熟知待定系数法、一次函数的图像与性质及坐 标的对称性． 25.如图，甲、乙两人（看成点）分别在数轴－3 和 5 的位置上，沿数轴做移动游戏．每次移动游戏规则：裁 判先捂住一枚硬币，再让两人猜向上一面是正是反，而后根据所猜结果进行移动． ①若都对或都错，则甲向东移动 1 个单位，同时乙向西移动 1 个单位； ②若甲对乙错，则甲向东移动 4 个单位，同时乙向东移动 2 个单位； ③若甲错乙对，则甲向西移动 2 个单位，同时乙向西移动 4 个单位． （1）经过第一次移动游戏，求甲的位置停留在正半轴上的概率 P ； （2）从图的位置开始，若完成了 10 次移动游戏，发现甲、乙每次所猜结果均为一对一错．设乙猜对 n 次， 且他最终．．停留的位置对应的数为 m ，试用含 的代数式表示 ，并求该位置距离原点 O 最近时 的值； （3）从图的位置开始，若进行了 k 次移动游戏后，甲与乙的位置相距 2 个单位，直接．．写出 的值． 【答案】（1） 1 4P  ；（ 2） 2 5 6mn；当 4n  时，距离原点最近；（3） 3k  或 5 【解析】 【分析】 （1）对题干中三种情况计算对应概率，分析出正确的概率即可； 硬币朝上为正面、反面的概率均为 1 2 ， 甲和乙猜正反的情况也分为三种情况： ①甲和乙都猜正面或反面，概率为 ， ②甲猜正，乙猜反，概率为 1 4 ， ③甲猜反，乙猜正，概率为 ， （2）根据题意可知乙答了 10 次，答对了 n 次，则打错了（10-n）次，再根据平移的规则推算出结果即可； （3）刚开始的距离是 8，根据三种情况算出缩小的距离，即可算出缩小的总距离，分别除以 2 即可得到结 果； 【详解】（1）题干中对应的三种情况的概率为： ① 11111 +=22222； ② 1 1 1 1 1+=2 4 2 4 4； ③ ； 甲的位置停留在正半轴上的位置对应情况②，故 P= ． （2）根据题意可知乙答了 10 次，答对了 n 次，则打错了（10-n）次， 根据题意可得，n 次答对，向西移动 4n， 10-n 次答错，向东移了 2（10-n）， ∴m=5-4n+2（10-n）=25-6n， ∴当 n=4 时，距离原点最近． （3）起初，甲乙的距离是 8， 易知，当甲乙一对一错时，二者之间距离缩小 2， 当甲乙同时答对打错时，二者之间的距离缩小 2， ∴当加一位置相距 2 个单位时，共缩小了 6 个单位或 10 个单位， ∴6 2=3 或10 2=5 ， ∴ 3k  或 5k  ． 【点睛】本题主要考查了概率的求解，通过数轴的理解进行准确分析是解题的关键． 26.如图 1 和图 2， 在 ABC 中，A B A C ， 8BC  ， 3ta n 4C  ．点 K 在 AC 边上，点 M ，N 分别在 AB ， BC 上，且 2A M C N．点 P 从点 出发沿折线 M B B N 匀速移动，到达点 时停止；而点 Q 在 边上随 移动，且始终保持 A P Q B   ． （1）当点 在 上时，求点 与点 A 的最短距离； （2）若点 在 MB 上，且 PQ 将 的面积分成上下 4：5 两部分时，求 MP 的长； （3）设点 移动的路程为 x ，当 03x及39x时，分别求点 到直线 的距离（用含 的式子 表示）； （4）在点 处设计并安装一扫描器，按定角 APQ 扫描 APQ 区域（含边界），扫描器随点 从 到 B 再到 共用时 36 秒．若 9 4AK  ，请直接．．写出点 被扫描到的总时长． 【答案】（1）3 ；（ 2） 4 3MP  ；（ 3）当 时， 24 48 25 25dx；当 时， 333 55dx  ； （4） 23ts 【解析】 【分析】 （1）根据当点 在 上时，PA⊥BC 时 PA 最小，即可求出答案； （2）过 A 点向 BC 边作垂线，交 BC 于点 E，证明△APQ∽△ABC，可得 2 APQ ABC S AP S AB     ，根据 S S 上 下 = 4 5 可 得 2 4= 9 APQ ABC S AP SAB     ，可得 2 3 AP AB  ，求出 AB=5，即可解出 MP； （3）先讨论当 0≤x≤3 时，P 在 BM 上运动，P 到 AC 的距离：d=PQ·sinC，求解即可，再讨论当 3≤x≤9 时， P 在 BN 上运动，BP=x-3，CP=8-（x-3）=11-x，根据 d=CP·sinC 即可得出答案； （4）先求出移动的速度= 9 36 = 1 4 ，然后先求出从 Q 平移到 K 耗时，再求出不能被扫描的时间段即可求出时 间． 【详解】（1）当点 P 在 BC 上时，PA⊥BC 时 PA 最小， ∵AB=AC，△ABC 为等腰三角形， ∴PA min=tanC· 2 BC = 3 4 ×4=3； （2）过 A 点向 BC 边作垂线，交 BC 于点 E， S 上=S△APQ， S 下=S 四边形 BPQC， ∵ APQB  ， ∴PQ∥BC， ∴△APQ∽△ABC， ∴ APADPQ ABACBC， ∴ ， 当 = 时， ， ∴ ， AE= 2 BC ·t a n 3C  ， 根据勾股定理可得 AB=5， ∴ 22 53 APMP AB ， 解得 MP= 4 3 ； （3）当 0≤x≤3 时，P 在 BM 上运动， P 到 AC 的距离：d=PQ·sinC， 由（2）可知 sinC= 3 5 ， ∴d= PQ， ∵AP=x+2， ∴ 2 5 APxPQ ABBC ， ∴PQ= 2 85 x   ， ∴d= 23855 x   = 2448 2525x  ， 当 3≤x≤9 时，P 在 BN 上运动， BP=x-3，CP=8-（x-3）=11-x， d=CP·sinC= （11-x）=- x+ 33 5 ， 综上     2448 032525 333 3955 xx d xx     ； （4）AM=2