中考数学模拟试卷四含解析 17页

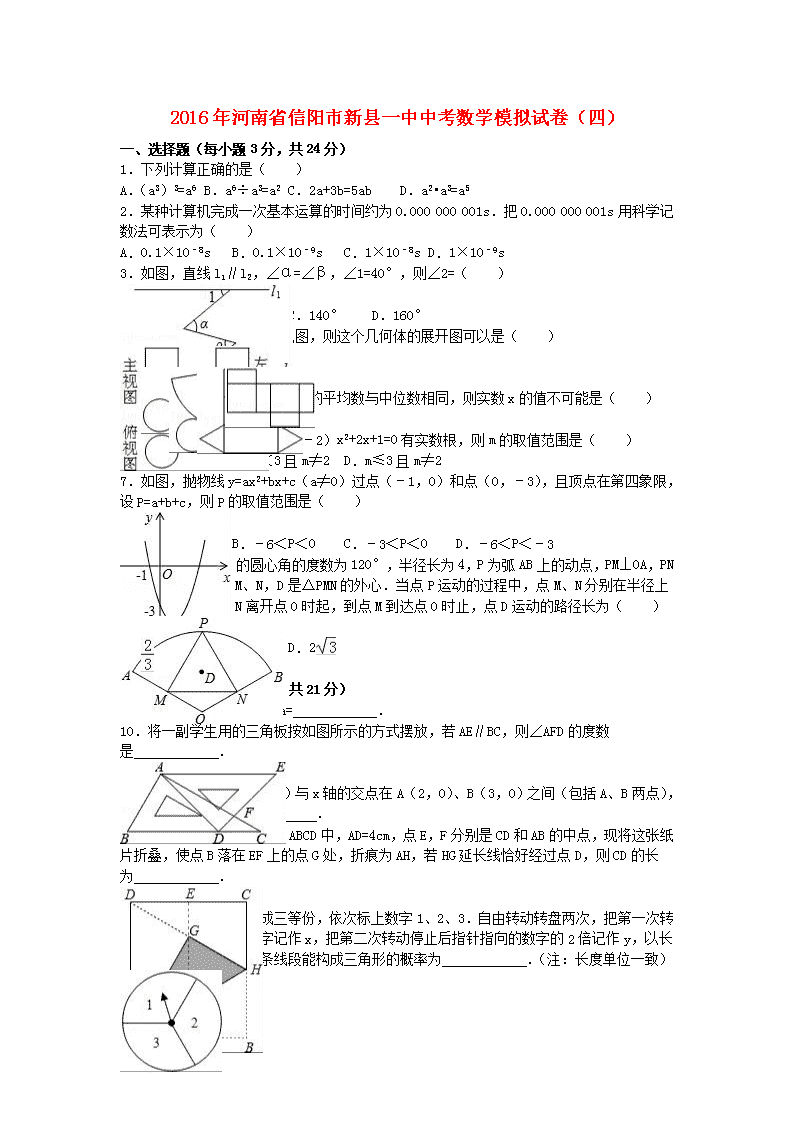
‎2016年河南省信阳市新县一中中考数学模拟试卷（四）‎ 一、选择题（每小题3分，共24分）‎ ‎1．下列计算正确的是（　　）‎ A．（a3）3=a6 B．a6÷a3=a2 C．2a+3b=5ab D．a2•a3=a5‎ ‎2．某种计算机完成一次基本运算的时间约为0.000 000 001s．把0.000 000 001s用科学记数法可表示为（　　）‎ A．0.1×10﹣8s B．0.1×10﹣9s C．1×10﹣8s D．1×10﹣9s ‎3．如图，直线l1∥l2，∠α=∠β，∠1=40°，则∠2=（　　）‎ A．100° B．120° C．140° D．160°‎ ‎4．如图是一个几何体的三视图，则这个几何体的展开图可以是（　　）‎ A． B． C． D．‎ ‎5．若一组数据1，2，3，4，x的平均数与中位数相同，则实数x的值不可能是（　　）‎ A．0 B．2.5 C．3 D．5‎ ‎6．关于x的一元二次方程（m﹣2）x2+2x+1=0有实数根，则m的取值范围是（　　）‎ A．m≤3 B．m＜3 C．m＜3且m≠2 D．m≤3且m≠2‎ ‎7．如图，抛物线y=ax2+bx+c（a≠0）过点（﹣1，0）和点（0，﹣3），且顶点在第四象限，设P=a+b+c，则P的取值范围是（　　）‎ A．﹣3＜P＜﹣1 B．﹣6＜P＜0 C．﹣3＜P＜0 D．﹣6＜P＜﹣3‎ ‎8．如图，扇形OAB的圆心角的度数为120°，半径长为4，P为弧AB上的动点，PM⊥OA，PN⊥OB，垂足分别为M、N，D是△PMN的外心．当点P运动的过程中，点M、N分别在半径上作相应运动，从点N离开点O时起，到点M到达点O时止，点D运动的路径长为（　　）‎ A．π B．π C．2 D．2‎ ‎　‎ 二、填空题（每小题3分，共21分）‎ ‎9．分解因式：ax2﹣4ax+4a=　　　　　　．‎ ‎10．将一副学生用的三角板按如图所示的方式摆放，若AE∥BC，则∠AFD的度数是　　　　　　．‎ ‎11．已知直线y=2x+（3﹣a）与x轴的交点在A（2，0）、B（3，0）之间（包括A、B两点），则a的取值范围是　　　　　　．‎ ‎12．如图，在一张矩形纸片ABCD中，AD=4cm，点E，F分别是CD和AB的中点，现将这张纸片折叠，使点B落在EF上的点G处，折痕为AH，若HG延长线恰好经过点D，则CD的长为　　　　　　．‎ ‎13．把一个转盘平均分成三等份，依次标上数字1、2、3．自由转动转盘两次，把第一次转动停止后指针指向的数字记作x，把第二次转动停止后指针指向的数字的2倍记作y，以长度分别为x、y、5的三条线段能构成三角形的概率为　　　　　　．（注：长度单位一致）‎ ‎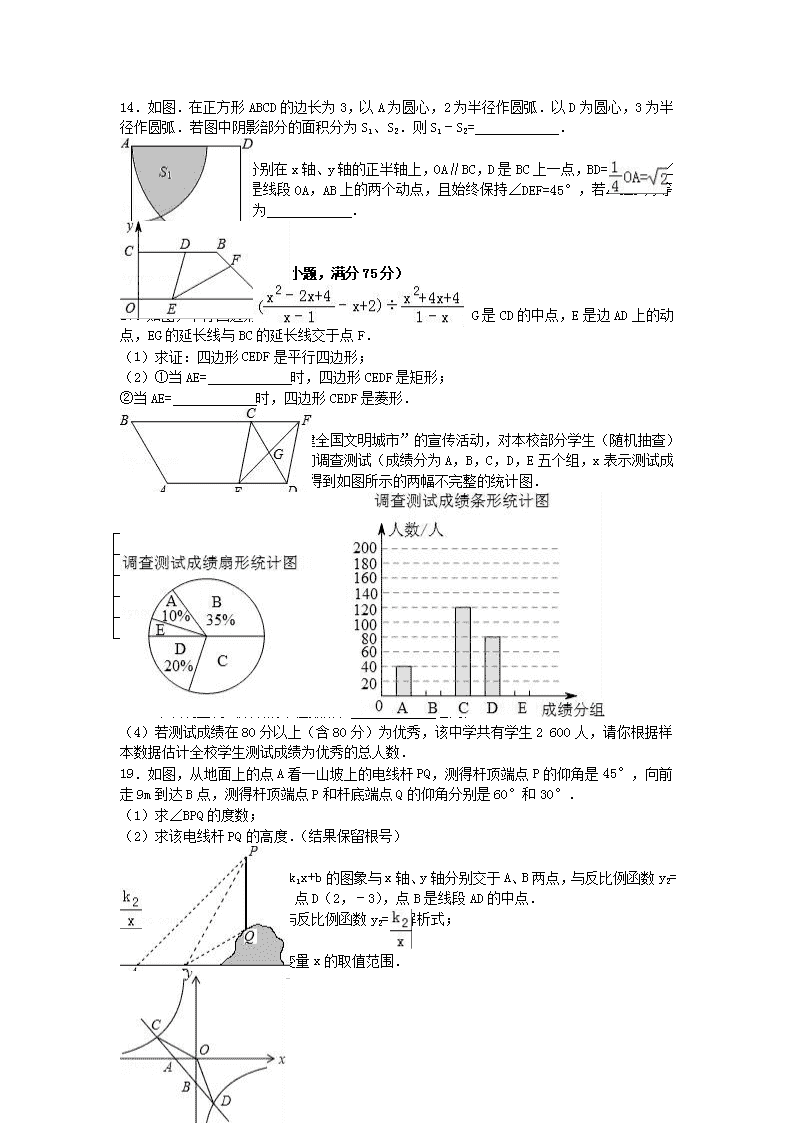14．如图．在正方形ABCD的边长为3，以A为圆心，2为半径作圆弧．以D为圆心，3为半径作圆弧．若图中阴影部分的面积分为S1、S2．则S1﹣S2=　　　　　　．‎ ‎15．如图，边OA，OC分别在x轴、y轴的正半轴上，OA∥BC，D是BC上一点，BD=，AB=3，∠OAB=45°，E，F分别是线段OA，AB上的两个动点，且始终保持∠DEF=45°，若△AEF为等腰三角形，则OE的长为　　　　　　．‎ ‎　‎ 三、解答题（本大题共8个小题，满分75分）‎ ‎16．先化简，再求值：，其中x满足x2﹣4x+3=0．‎ ‎17．如图，平行四边形ABCD中，AB=3，BC=5，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F．‎ ‎（1）求证：四边形CEDF是平行四边形；‎ ‎（2）①当AE=　　　　　　时，四边形CEDF是矩形；‎ ‎②当AE=　　　　　　时，四边形CEDF是菱形．‎ ‎18．某市某中学为了搞好“创建全国文明城市”的宣传活动，对本校部分学生（随机抽查）进行了一次相关知识了解程度的调查测试（成绩分为A，B，C，D，E五个组，x表示测试成绩）．通过对测试成绩的分析，得到如图所示的两幅不完整的统计图．‎ 调查测试成绩分组表 A组：90≤x≤100‎ B组：80≤x＜90‎ C组：70≤x＜80‎ D组：60≤x＜70‎ E组：x＜60‎ 请你根据图中提供的信息解答以下问题：‎ ‎（1）参加调查测试的学生为　　　　　　人；‎ ‎（2）将条形统计图补充完整；‎ ‎（3）本次调查测试成绩的中位数落在　　　　　　组内；‎ ‎（4）若测试成绩在80分以上（含80分）为优秀，该中学共有学生2 600人，请你根据样本数据估计全校学生测试成绩为优秀的总人数．‎ ‎19．如图，从地面上的点A看一山坡上的电线杆PQ，测得杆顶端点P的仰角是45°，向前走9m到达B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°．‎ ‎（1）求∠BPQ的度数；‎ ‎（2）求该电线杆PQ的高度．（结果保留根号）‎ ‎20．如图，已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点，与反比例函数y2=的图象分别交于C、D两点，点D（2，﹣3），点B是线段AD的中点．‎ ‎（1）求一次函数y1=k1x+b与反比例函数y2=的解析式；‎ ‎（2）求△COD的面积；‎ ‎（3）直接写出y1＞y2时自变量x的取值范围．‎ ‎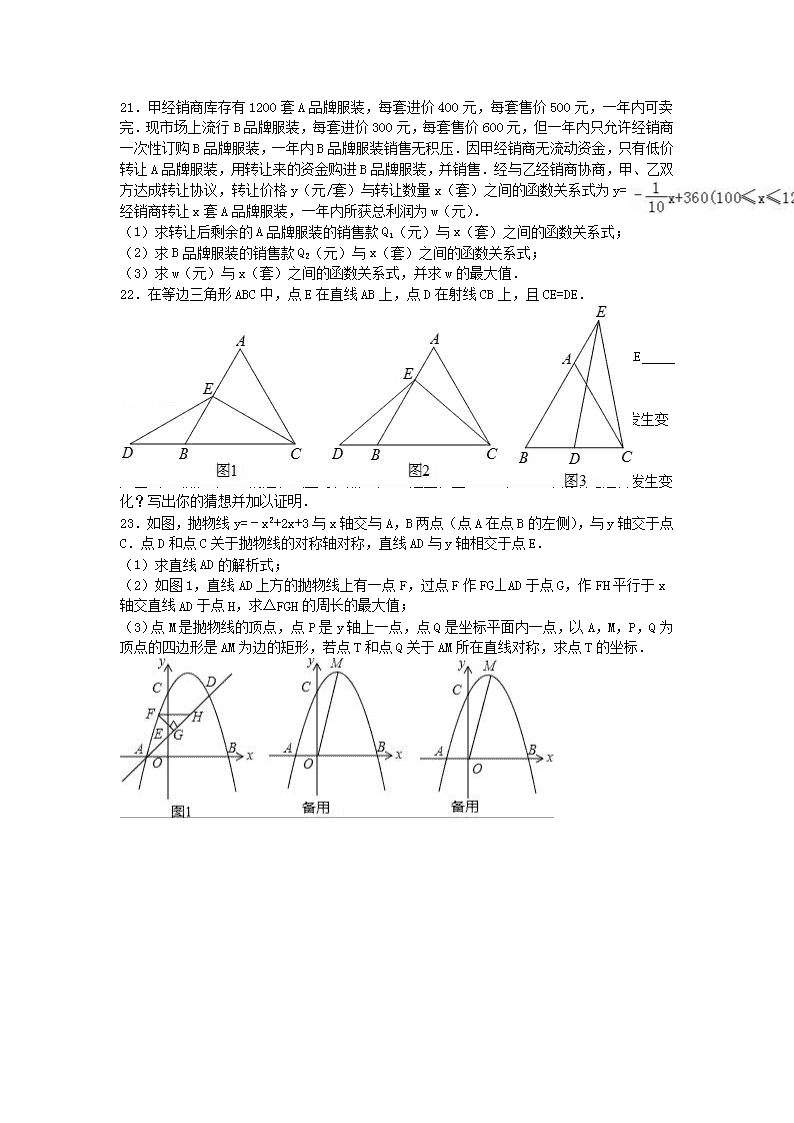21．甲经销商库存有1200套A品牌服装，每套进价400元，每套售价500元，一年内可卖完．现市场上流行B品牌服装，每套进价300元，每套售价600元，但一年内只允许经销商一次性订购B品牌服装，一年内B品牌服装销售无积压．因甲经销商无流动资金，只有低价转让A品牌服装，用转让来的资金购进B品牌服装，并销售．经与乙经销商协商，甲、乙双方达成转让协议，转让价格y（元/套）与转让数量x（套）之间的函数关系式为y=．若甲经销商转让x套A品牌服装，一年内所获总利润为w（元）．‎ ‎（1）求转让后剩余的A品牌服装的销售款Q1（元）与x（套）之间的函数关系式；‎ ‎（2）求B品牌服装的销售款Q2（元）与x（套）之间的函数关系式；‎ ‎（3）求w（元）与x（套）之间的函数关系式，并求w的最大值．‎ ‎22．在等边三角形ABC中，点E在直线AB上，点D在射线CB上，且CE=DE．‎ ‎（1）特殊情况，探索结论 如图1，当点E是AB中点时，确定线段AE与BD的大小关系，请你直接写出结论：AE　　　　　　BD（填“＞”、“＜”或“=”）．‎ ‎（2）特例启发，问题探究 如图2，当点E是线段AB上除端点和中点外的任一点时，此时，（1）中的结论是否发生变化？写出你的猜想并加以证明．‎ ‎（3）拓展延伸 如图3，当点E在BA的延长线上时，点D在BC边上，且CE=DE，（1）中的结论是否发生变化？写出你的猜想并加以证明．‎ ‎23．如图，抛物线y=﹣x2+2x+3与x轴交与A，B两点（点A在点B的左侧），与y轴交于点C．点D和点C关于抛物线的对称轴对称，直线AD与y轴相交于点E．‎ ‎（1）求直线AD的解析式；‎ ‎（2）如图1，直线AD上方的抛物线上有一点F，过点F作FG⊥AD于点G，作FH平行于x轴交直线AD于点H，求△FGH的周长的最大值；‎ ‎（3）点M是抛物线的顶点，点P是y轴上一点，点Q是坐标平面内一点，以A，M，P，Q为顶点的四边形是AM为边的矩形，若点T和点Q关于AM所在直线对称，求点T的坐标．‎ ‎　‎ ‎2016年河南省信阳市新县一中中考数学模拟试卷（四）‎ 参考答案与试题解析 ‎　‎ 一、选择题（每小题3分，共24分）‎ ‎1．下列计算正确的是（　　）‎ A．（a3）3=a6 B．a6÷a3=a2 C．2a+3b=5ab D．a2•a3=a5‎ ‎【考点】同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方．‎ ‎【分析】结合选项分别进行同底数幂的除法、合并同类项、同底数幂的乘法、幂的乘方和积的乘方等运算，然后选择正确选项．‎ ‎【解答】解：A、（a3）3=a9，原式计算错误，故本选项错误；‎ B、a6÷a3=a3，原式计算错误，故本选项错误；‎ C、2a和3b不是同类项，不能合并，故本选项错误；‎ D、a2•a3=a5，原式正确，故本选项正确．‎ 故选D．‎ ‎　‎ ‎2．某种计算机完成一次基本运算的时间约为0.000 000 001s．把0.000 000 001s用科学记数法可表示为（　　）‎ A．0.1×10﹣8s B．0.1×10﹣9s C．1×10﹣8s D．1×10﹣9s ‎【考点】科学记数法—表示较小的数．‎ ‎【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．‎ ‎【解答】解：0.000 000 001=1×10﹣9，‎ 故选：D．‎ ‎　‎ ‎3．如图，直线l1∥l2，∠α=∠β，∠1=40°，则∠2=（　　）‎ A．100° B．120° C．140° D．160°‎ ‎【考点】平行线的性质．‎ ‎【分析】先根据平行线的性质，由l1∥l2得∠3=∠1=40°，再根据平行线的判定，由∠α=∠β得AB∥CD，然后根据平行线的性质得∠2+∠3=180°，再把∠1=40°代入计算即可．‎ ‎【解答】解：如图，‎ ‎∵l1∥l2，‎ ‎∴∠3=∠1=40°，‎ ‎∵∠α=∠β，‎ ‎∴AB∥CD，‎ ‎∴∠2+∠3=180°，‎ ‎∴∠2=180°﹣∠3=180°﹣40°=140°．‎ 故选C．‎ ‎　‎ ‎4．如图是一个几何体的三视图，则这个几何体的展开图可以是（　　）‎ A． B． C． D．‎ ‎【考点】由三视图判断几何体；几何体的展开图．‎ ‎【分析】由三视图的特征，可得这个几何体应该是圆柱；‎ ‎【解答】解：根据题意，这个几何体是圆柱；‎ 其展开图为：‎ 故选A．‎ ‎　‎ ‎5．若一组数据1，2，3，4，x的平均数与中位数相同，则实数x的值不可能是（　　）‎ A．0 B．2.5 C．3 D．5‎ ‎【考点】中位数；算术平均数．‎ ‎【分析】因为中位数的值与大小排列顺序有关，而此题中x的大小位置未定，故应该分类讨论x所处的所有位置情况：从小到大（或从大到小）排列在中间；结尾；开始的位置．‎ ‎【解答】解：（1）将这组数据从小到大的顺序排列为1，2，3，4，x，‎ 处于中间位置的数是3，‎ ‎∴中位数是3，‎ 平均数为（1+2+3+4+x）÷5，‎ ‎∴3=（1+2+3+4+x）÷5，‎ 解得x=5；符合排列顺序；‎ ‎（2）将这组数据从小到大的顺序排列后1，2，3，x，4，‎ 中位数是3，‎ 此时平均数是（1+2+3+4+x）÷5=3，‎ 解得x=5，不符合排列顺序；‎ ‎（3）将这组数据从小到大的顺序排列后1，x，2，3，4，‎ 中位数是2，‎ 平均数（1+2+3+4+x）÷5=2，‎ 解得x=0，不符合排列顺序；‎ ‎（4）将这组数据从小到大的顺序排列后x，1，2，3，4，‎ 中位数是2，‎ 平均数（1+2+3+4+x）÷5=2，‎ 解得x=0，符合排列顺序；‎ ‎（5）将这组数据从小到大的顺序排列后1，2，x，3，4，‎ 中位数，x，‎ 平均数（1+2+3+4+x）÷5=x，‎ 解得x=2.5，符合排列顺序；‎ ‎∴x的值为0、2.5或5．‎ 故选C．‎ ‎　‎ ‎6．关于x的一元二次方程（m﹣2）x2+2x+1=0有实数根，则m的取值范围是（　　）‎ A．m≤3 B．m＜3 C．m＜3且m≠2 D．m≤3且m≠2‎ ‎【考点】根的判别式；一元二次方程的定义．‎ ‎【分析】根据一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2﹣4ac的意义得到m﹣2≠0且△≥0，即22﹣4×（m﹣2）×1≥0，然后解不等式组即可得到m的取值范围．‎ ‎【解答】解：∵关于x的一元二次方程（m﹣2）x2+2x+1=0有实数根，‎ ‎∴m﹣2≠0且△≥0，即22﹣4×（m﹣2）×1≥0，解得m≤3，‎ ‎∴m的取值范围是 m≤3且m≠2．‎ 故选：D．‎ ‎　‎ ‎7．如图，抛物线y=ax2+bx+c（a≠0）过点（﹣1，0）和点（0，﹣3），且顶点在第四象限，设P=a+b+c，则P的取值范围是（　　）‎ A．﹣3＜P＜﹣1 B．﹣6＜P＜0 C．﹣3＜P＜0 D．﹣6＜P＜﹣3‎ ‎【考点】二次函数图象与系数的关系．‎ ‎【分析】利用二次函数图象的开口方向和对称轴求出a＞0，b＜0，把x=﹣1代入求出b=a﹣3，把x=1代入得出P=a+b+c=2a﹣6，求出2a﹣6的范围即可．‎ ‎【解答】解：∵抛物线y=ax2+bx+c（c≠0）过点（﹣1，0）和点（0，﹣3），‎ ‎∴0=a﹣b+c，﹣3=c，‎ ‎∴b=a﹣3，‎ ‎∵当x=1时，y=ax2+bx+c=a+b+c，‎ ‎∴P=a+b+c=a+a﹣3﹣3=2a﹣6，‎ ‎∵顶点在第四象限，a＞0，‎ ‎∴b=a﹣3＜0，‎ ‎∴a＜3，‎ ‎∴0＜a＜3，‎ ‎∴﹣6＜2a﹣6＜0，‎ 即﹣6＜P＜0．‎ 故选：B．‎ ‎　‎ ‎8．如图，扇形OAB的圆心角的度数为120°，半径长为4，P为弧AB上的动点，PM⊥OA，PN⊥OB，垂足分别为M、N，D是△PMN的外心．当点P运动的过程中，点M、N分别在半径上作相应运动，从点N离开点O时起，到点M到达点O时止，点D运动的路径长为（　　）‎ A．π B．π C．2 D．2‎ ‎【考点】弧长的计算；轨迹．‎ ‎【分析】根据题意画出点N离开点O时，到点M到达点O时的图形，得到点D运动的轨迹，根据弧长公式计算即可．‎ ‎【解答】解：当点N与点O重合时，∠P′OA=30°，OD=OP′=2，‎ 当点M与点O重合时，∠P′′OB=30°，OD=OP′′=2，‎ ‎∵D是△PMN的外心，‎ ‎∴点D在线段PM的垂直平分线上，又PM⊥OA，‎ ‎∴D为OP的中点，即OD=OP=2，‎ ‎∴点D运动的轨迹是以点O为圆心，2为半径，圆心角为60°的弧，‎ 弧长为： =．‎ 故选：A．‎ ‎　‎ 二、填空题（每小题3分，共21分）‎ ‎9．分解因式：ax2﹣4ax+4a=　a（x﹣2）2　．‎ ‎【考点】提公因式法与公式法的综合运用．‎ ‎【分析】先提取公因式a，再利用完全平方公式进行二次分解．‎ ‎【解答】解：ax2﹣4ax+4a，‎ ‎=a（x2﹣4x+4），‎ ‎=a（x﹣2）2．‎ ‎　‎ ‎10．将一副学生用的三角板按如图所示的方式摆放，若AE∥BC，则∠AFD的度数是　75°　．‎ ‎【考点】平行线的性质．‎ ‎【分析】先根据平行线的性质得出∠B+∠BAE=180°，再由直角三角板的性质得出∠B=60°，∠BAC=90°，∠EAD=45°，故可得出∠EAF的度数，再由三角形外角的性质即可得出结论．‎ ‎【解答】解：∵AE∥BC，‎ ‎∴∠B+∠BAE=180°，‎ ‎∵两三角板是一副直角三角板，‎ ‎∴∠B=60°，∠BAC=90°，∠EAD=45°，‎ ‎∴∠BAE=120°，‎ ‎∴∠EAF=BAE﹣∠BAC=120°﹣90°=30°，‎ ‎∵∠AFD是△AEF的外角，‎ ‎∴∠AFD=∠E+∠EAF=45°+30°=75°．‎ 故答案为75°．‎ ‎　‎ ‎11．已知直线y=2x+（3﹣a）与x轴的交点在A（2，0）、B（3，0）之间（包括A、B两点），则a的取值范围是　7≤a≤9　．‎ ‎【考点】一次函数图象上点的坐标特征．‎ ‎【分析】根据题意得到x的取值范围是2≤x≤3，则通过解关于x的方程2x+（3﹣a）=0求得x的值，由x的取值范围来求a的取值范围．‎ ‎【解答】解：∵直线y=2x+（3﹣a）与x轴的交点在A（2，0）、B（3，0）之间（包括A、B两点），‎ ‎∴2≤x≤3，‎ 令y=0，则2x+（3﹣a）=0，‎ 解得x=，‎ 则2≤≤3，‎ 解得7≤a≤9．‎ 故答案是：7≤a≤9．‎ ‎　‎ ‎12．如图，在一张矩形纸片ABCD中，AD=4cm，点E，F分别是CD和AB的中点，现将这张纸片折叠，使点B落在EF上的点G处，折痕为AH，若HG延长线恰好经过点D，则CD的长为　2cm　．‎ ‎【考点】翻折变换（折叠问题）．‎ ‎【分析】如图，首先证明AG为线段DH的垂直平分线；进而证明AD=AH=4，∠DAG=∠HAG=∠HAB=α，求出α；运用直角三角形的边角关系求出AB，即可解决问题．‎ ‎【解答】解：如图，∵点E，F分别是CD和AB的中点，‎ 且四边形ABCD为矩形，‎ ‎∴EG∥CH，而DE=CE，‎ ‎∴DG=GH；由题意得：∠AGH=∠B=90°，‎ ‎∴AG为线段DH的垂直平分线，‎ ‎∴AD=AH=4，∠DAG=∠HAG（设为α）；‎ 而∠BAH=∠GAH=α，‎ ‎∴3α=90°，α=30°，‎ ‎∴cos30°=，AB=2（cm），‎ ‎∴CD=AB=2cm，‎ 故答案为2cm．‎ ‎　‎ ‎13．把一个转盘平均分成三等份，依次标上数字1、2、3．自由转动转盘两次，把第一次转动停止后指针指向的数字记作x，把第二次转动停止后指针指向的数字的2倍记作y，以长度分别为x、y、5的三条线段能构成三角形的概率为　　．（注：长度单位一致）‎ ‎【考点】列表法与树状图法；三角形三边关系．‎ ‎【分析】依据题意先用列表法或画树状图法分析所有等可能的出现结果，然后根据概率公式求出该事件的概率．‎ ‎【解答】解：列表得：‎ x y ‎1‎ ‎2‎ ‎3‎ ‎1‎ ‎（1，2）‎ ‎（2，2）‎ ‎（3，2）‎ ‎2‎ ‎（1，4）‎ ‎（2，4）‎ ‎（3，4）‎ ‎3‎ ‎（1，6）‎ ‎（2，6）‎ ‎（3，6）‎ 因此，点A（x，y）的个数共有9个；‎ 则x、y、5的三条线段能构成三角形的有4组：2，4，5；3，4，5；2，6，5；3，6，5；‎ 可得P=．‎ 故答案为：．‎ ‎　‎ ‎14．如图．在正方形ABCD的边长为3，以A为圆心，2为半径作圆弧．以D为圆心，3为半径作圆弧．若图中阴影部分的面积分为S1、S2．则S1﹣S2=　﹣9　．‎ ‎【考点】整式的加减．‎ ‎【分析】先求出正方形的面积，再根据扇形的面积公式求出以A为圆心，2为半径作圆弧、以D为圆心，3为半径作圆弧的两扇形面积，再求出其差即可．‎ ‎【解答】解：∵S正方形=3×3=9，‎ S扇形ADC==，‎ S扇形EAF==π，‎ ‎∴S1﹣S2=S扇形EAF﹣（S正方形﹣S扇形ADC）=π﹣（9﹣）=﹣9．‎ 故答案为：﹣9．‎ ‎　‎ ‎15．如图，边OA，OC分别在x轴、y轴的正半轴上，OA∥BC，D是BC上一点，BD=，AB=3，∠OAB=45°，E，F分别是线段OA，AB上的两个动点，且始终保持∠DEF=45°，若△AEF为等腰三角形，则OE的长为　　．‎ ‎【考点】等腰三角形的性质；坐标与图形性质．‎ ‎【分析】因为△AEF为等腰三角形，所以要分三种情况进行讨论：①当EF=AF时，如图1，根据△AGB是直角三角形及斜边AB=3可求AG的长，即BG的长，从而求出AE的长，相减即可得出OE；‎ ‎②当EF=AE时，如图2，AE=BD=，则OE=OA﹣AE即可；‎ ‎③当AE=AF时，如图3，证明△ODE是等腰三角形，再求OD的长，就是OE的长．‎ ‎【解答】解：当△AEF为等腰三角形，存在3种情况：‎ ‎①当EF=AF时，如图1，过点B作BG⊥x轴于G，则△AGB是直角三角形，‎ ‎∵BD=，‎ ‎∴OA=4，‎ ‎∵∠OAB=45°，‎ ‎∴△AEF是等腰直角三角形，‎ ‎∵∠DEF=45°，‎ ‎∴∠DEA=90°，‎ 则四边形DEGB是平行四边形，‎ ‎∵AB=3，‎ ‎∴AG=BG=，‎ ‎∴AE=AG+EG=+BD=+=，‎ ‎∴OE=OA﹣AE=4﹣=；‎ ‎②当EF=AE时，如图2，‎ ‎∵∠OAB=45°，‎ ‎∴∠EFA=∠OAB=45°，‎ ‎∴∠FEA=90°，‎ ‎∵∠DEF=45°，‎ ‎∴∠DEO=180°﹣90°﹣45°=45°，‎ ‎∴∠DEO=∠OAB，‎ ‎∴OE∥AB，‎ ‎∵BC∥OA，‎ ‎∴四边形DEAB是平行四边形，‎ ‎∴AE=BD=，‎ ‎∴OE=4﹣=3；‎ ‎③当AE=AF时，如图3，‎ ‎∵∠OAB=45°，‎ ‎∴∠FEA=67.5°，‎ ‎∵∠DEF=45°，‎ ‎∴∠OED=180°﹣45°﹣67.5°=67.5°，‎ 由（1）得：AG=BG=，‎ ‎∴CD=OA﹣AG﹣BD=4﹣﹣=，‎ ‎∴CD=OC=，‎ ‎∴△COD是等腰直角三角形，则OD=CD=3，‎ ‎∴∠COD=45°，‎ ‎∴∠DOE=45°，‎ ‎∴∠ODE=180°﹣45°﹣67.5°=67.5°，‎ ‎∴∠ODE=∠OED，‎ ‎∴OD=OE=3‎ 综上所述：OE=或3或3．‎ ‎　‎ 三、解答题（本大题共8个小题，满分75分）‎ ‎16．先化简，再求值：，其中x满足x2﹣4x+3=0．‎ ‎【考点】分式的化简求值．‎ ‎【分析】先根据分式混合运算的法则把原式进行化简，再求出x的值代入进行计算即可．‎ ‎【解答】解：原式=[﹣]÷=×=×=﹣，‎ ‎∵x满足x2﹣4x+3=0，‎ ‎∴（x﹣3）（x﹣1）=0，‎ ‎∴x1=3，x2=1，‎ 当x=3时，原式=﹣=﹣；‎ 当x=1时，原式无意义．‎ 故分式的值为﹣．‎ ‎　‎ ‎17．如图，平行四边形ABCD中，AB=3，BC=5，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F．‎ ‎（1）求证：四边形CEDF是平行四边形；‎ ‎（2）①当AE=　3.5　时，四边形CEDF是矩形；‎ ‎②当AE=　2　时，四边形CEDF是菱形．‎ ‎【考点】平行四边形的判定与性质；全等三角形的判定与性质；菱形的判定；矩形的判定．‎ ‎【分析】（1）证△CFG≌△EDG，推出FG=EG，根据平行四边形的判定推出即可；‎ ‎（2）①求出△MBA≌△EDC，推出∠CED=∠AMB=90°，根据矩形的判定推出即可；‎ ‎②求出△CDE是等边三角形，推出CE=DE，根据菱形的判定推出即可．‎ ‎【解答】（1）证明：四边形ABCD是平行四边形，‎ ‎∴CF∥ED，‎ ‎∴∠FCD=∠GCD，‎ 又∠CGF=∠EGD．‎ G是CD的中点，‎ CG=DG，‎ 在△FCG和△EDG中，‎ ‎∴△CFG≌△EDG（ASA），‎ ‎∴FG=EG，‎ ‎∵CG=DG，‎ ‎∴四边形CEDF是平行四边形；‎ ‎（2）①解：当AE=3.5时，平行四边形CEDF是矩形，‎ 理由是：过A作AM⊥BC于M，‎ ‎∵∠B=60°，AB=3，‎ ‎∴BM=1.5，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴∠CDA=∠B=60°，DC=AB=3，BC=AD=5，‎ ‎∵AE=3.5，‎ ‎∴DE=1.5=BM，‎ 在△MBA和△EDC中，‎ ‎∴△MBA≌△EDC（SAS），‎ ‎∴∠CED=∠AMB=90°，‎ ‎∵四边形CEDF是平行四边形，‎ ‎∴四边形CEDF是矩形，‎ 故答案为：3.5；‎ ‎②当AE=2时，四边形CEDF是菱形，‎ 理由是：∵AD=5，AE=2，‎ ‎∴DE=3，‎ ‎∵CD=3，∠CDE=60°，‎ ‎∴△CDE是等边三角形，‎ ‎∴CE=DE，‎ ‎∵四边形CEDF是平行四边形，‎ ‎∴四边形CEDF是菱形，‎ 故答案为：2．‎ ‎　‎ ‎18．某市某中学为了搞好“创建全国文明城市”的宣传活动，对本校部分学生（随机抽查）进行了一次相关知识了解程度的调查测试（成绩分为A，B，C，D，E五个组，x表示测试成绩）．通过对测试成绩的分析，得到如图所示的两幅不完整的统计图．‎ 调查测试成绩分组表 A组：90≤x≤100‎ B组：80≤x＜90‎ C组：70≤x＜80‎ D组：60≤x＜70‎ E组：x＜60‎ 请你根据图中提供的信息解答以下问题：‎ ‎（1）参加调查测试的学生为　400　人；‎ ‎（2）将条形统计图补充完整；‎ ‎（3）本次调查测试成绩的中位数落在　C　组内；‎ ‎（4）若测试成绩在80分以上（含80分）为优秀，该中学共有学生2 600人，请你根据样本数据估计全校学生测试成绩为优秀的总人数．‎ ‎【考点】条形统计图；用样本估计总体；扇形统计图；中位数．‎ ‎【分析】（1）根据A类人数是40，所占的百分比是10%，据此即可求得总人数；‎ ‎（2）根据百分比的定义求得B和E类的人数，从而完成条形统计图；‎ ‎（3）利用中位数的定义，就是大小处于中间位置的数即可作判断．‎ ‎（4）利用总人数乘以对应的百分比即可求解．‎ ‎【解答】解：（1）参加调查测试的学生总数是：40÷10%=400（人），‎ 故答案是：400；‎ ‎（2）B组的人数是：400×35%=140（人），‎ 则E组的人数是：400﹣40﹣140﹣120﹣80=20（人）．‎ ‎；‎ ‎（3）∵A组有40人，B组有140人，C组有120人，‎ ‎∴400的最中间在C组范围内，‎ ‎∴中位数落在C组．‎ 故答案是：C；‎ ‎（4）全校学生测试成绩为优秀的总人数是：2600×（10%+35%）=1170（人），‎ 答：全校学生测试成绩为优秀的总人数约为1170人．‎ ‎　‎ ‎19．如图，从地面上的点A看一山坡上的电线杆PQ，测得杆顶端点P的仰角是45°，向前走9m到达B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°．‎ ‎（1）求∠BPQ的度数；‎ ‎（2）求该电线杆PQ的高度．（结果保留根号）‎ ‎【考点】解直角三角形的应用-仰角俯角问题．‎ ‎【分析】（1）延长PQ交直线AB于点E，根据直角三角形两锐角互余求得即可；‎ ‎（2）设PE=x米，在直角△APE和直角△BPE中，根据三角函数利用x表示出AE和BE，根据AB=AE﹣BE即可列出方程求得x的值，再在直角△BQE中利用三角函数求得QE的长，则PQ的长度即可求解．‎ ‎【解答】解：延长PQ交直线AB于点E，如图所示：‎ ‎（1）∠BPQ=90°﹣60°=30°；‎ ‎（2）设PE=x米．‎ 在直角△APE中，∠A=45°，‎ 则AE=PE=x米；‎ ‎∵∠PBE=60°，‎ ‎∴∠BPE=30°，‎ 在直角△BPE中，BE=PE=x米，‎ ‎∵AB=AE﹣BE=9米，‎ 则x﹣x=9，‎ 解得：x=．‎ 则BE=米．‎ 在直角△BEQ中，QE=BE=米．‎ ‎∴PQ=PE﹣QE=﹣=9+3（米）．‎ 答：电线杆PQ的高度为（9+3）米．‎ ‎　‎ ‎20．如图，已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点，与反比例函数y2=的图象分别交于C、D两点，点D（2，﹣3），点B是线段AD的中点．‎ ‎（1）求一次函数y1=k1x+b与反比例函数y2=的解析式；‎ ‎（2）求△COD的面积；‎ ‎（3）直接写出y1＞y2时自变量x的取值范围．‎ ‎【考点】反比例函数与一次函数的交点问题．‎ ‎【分析】（1）把点D的坐标代入y2=利用待定系数法即可求得反比例函数的解析式，作DE⊥x轴于E，根据题意求得A的坐标，然后利用待定系数法求得一次函数的解析式；‎ ‎（2）联立方程求得C的坐标，然后根据S△COD=S△AOC+S△AOD即可求得△COD的面积；‎ ‎（3）根据图象即可求得．‎ ‎【解答】解：∵点D（2，﹣3）在反比例函数y2=的图象上，‎ ‎∴k2=2×（﹣3）=﹣6，‎ ‎∴y2=﹣；‎ 作DE⊥x轴于E，‎ ‎∵D（2，﹣3），点B是线段AD的中点，‎ ‎∴A（﹣2，0），‎ ‎∵A（﹣2，0），D（2，﹣3）在y1=k1x+b的图象上，‎ ‎∴，‎ 解得k1=﹣，b=﹣，‎ ‎∴y1=﹣x﹣；‎ ‎（2）由，解得，，‎ ‎∴C（﹣4，），‎ ‎∴S△COD=S△AOC+S△AOD=×+×2×3=；‎ ‎（3）当x＜﹣4或0＜x＜2时，y1＞y2．‎ ‎　‎ ‎21．甲经销商库存有1200套A品牌服装，每套进价400元，每套售价500元，一年内可卖完．现市场上流行B品牌服装，每套进价300元，每套售价600元，但一年内只允许经销商一次性订购B品牌服装，一年内B品牌服装销售无积压．因甲经销商无流动资金，只有低价转让A品牌服装，用转让来的资金购进B品牌服装，并销售．经与乙经销商协商，甲、乙双方达成转让协议，转让价格y（元/套）与转让数量x（套）之间的函数关系式为y=．若甲经销商转让x套A品牌服装，一年内所获总利润为w（元）．‎ ‎（1）求转让后剩余的A品牌服装的销售款Q1（元）与x（套）之间的函数关系式；‎ ‎（2）求B品牌服装的销售款Q2（元）与x（套）之间的函数关系式；‎ ‎（3）求w（元）与x（套）之间的函数关系式，并求w的最大值．‎ ‎【考点】二次函数的应用．‎ ‎【分析】（1）直接根据销售款=售价×套数即可得出结论；‎ ‎（2）根据转让价格y（元/套）与转让数量x（套）之间的函数关系式为y=﹣x+360得出总件数，再与售价相乘即可；‎ ‎（3）把（1）（2）中的销售款相加再减去成本即可．‎ ‎【解答】解：（1）∵甲经销商库存有1200套A品牌服装，每套售价500元，转让x套给乙，‎ ‎∴Q1=500×=﹣500x+600000；‎ ‎（2）∵转让价格y（元/套）与转让数量x（套）之间的函数关系式为y=﹣x+360，B品牌服装，每套进价300元，‎ ‎∴转让后可购买B服装套，‎ ‎∴Q2=×600=﹣x2+720x；‎ ‎（3）∵由（1）、（2）知，Q1=﹣500x+600000，Q2=﹣x2+720x，‎ ‎∴W=Q1+Q2﹣400×1200‎ ‎=﹣500x+600000﹣x2+720x﹣480000‎ ‎=﹣（x﹣550）2+180500，‎ 当x=550时，W有最大值，最大值为180500元．‎ ‎　‎ ‎22．在等边三角形ABC中，点E在直线AB上，点D在射线CB上，且CE=DE．‎ ‎（1）特殊情况，探索结论 如图1，当点E是AB中点时，确定线段AE与BD的大小关系，请你直接写出结论：AE　=　BD（填“＞”、“＜”或“=”）．‎ ‎（2）特例启发，问题探究 如图2，当点E是线段AB上除端点和中点外的任一点时，此时，（1）中的结论是否发生变化？写出你的猜想并加以证明．‎ ‎（3）拓展延伸 如图3，当点E在BA的延长线上时，点D在BC边上，且CE=DE，（1）中的结论是否发生变化？写出你的猜想并加以证明．‎ ‎【考点】三角形综合题．‎ ‎【分析】（1）根据等边三角形的性质得到∠BCE=30°，AE=BE，根据等腰三角形的性质得到∠D=∠ECD=30°，根据三角形的外角的性质得到∠DEB=30°即可得到结论；‎ ‎（2）如图2，过E作EF∥BC交AC于F，根据等边三角形的性质得到∠ABC=∠ACB=60°，根据平行线的性质得到∠AEF=∠AFE=60°推出△AEF是等边三角形，根据全等三角形的性质得到BD=FE，等量代换得到结论；‎ ‎（3）过E作EF∥BC交CA的延长线于F，于是得到∠1=∠F，根据等边三角形的性质得到∠EAF=∠2=∠F=60°，根据全等三角形的性质得到BD=EF，等量代换得到结论．‎ ‎【解答】解：（1）∵△ABC是等边三角形，点E是AB中点，‎ ‎∴∠BCE=30°，AE=BE，‎ ‎∵DE=CE，‎ ‎∴∠D=∠ECD=30°，‎ ‎∵∠ABC=60°，‎ ‎∴∠DEB=30°，‎ ‎∴∠D=∠DEB，‎ ‎∴BD=BE，‎ ‎∴AE=BD；‎ ‎（2）（1）中的结论不发生变化，‎ 理由：如图2，过E作EF∥BC交AC于F，‎ ‎∵△ABC是等边三角形，‎ ‎∴∠ABC=∠ACB=60°，‎ ‎∴∠AEF=∠AFE=60°，∠3=120°，‎ ‎∴△AEF是等边三角形，‎ ‎∴AE=EF，∠4=120°，‎ ‎∴∠3=∠4，‎ ‎∵DE=CE，‎ ‎∴∠D=∠1，‎ ‎∴∠D=∠2，‎ 在△BDE与△FEC中，，‎ ‎∴△BDE≌△FEC，‎ ‎∴BD=FE，‎ ‎∴AE=BD；‎ ‎（3）不发生变化，‎ 理由：过E作EF∥BC交CA的延长线于F，‎ ‎∴∠1=∠F，∠BCE+∠CEF=180°，‎ ‎∵∠B=∠1=∠BAC=60°，‎ ‎∴∠EAF=∠2=∠F=60°，‎ ‎∴AE=EF，∠F=∠B，‎ ‎∵DE=CE，‎ ‎∴∠3=∠BCE，‎ ‎∵∠3+∠4=180°，‎ ‎∴∠4=∠CEF，‎ 在△BDE与△FEC中，，‎ ‎∴△BDE≌△FEC，‎ ‎∴BD=EF，‎ ‎∴AE=BD．‎ ‎　‎ ‎23．如图，抛物线y=﹣x2+2x+3与x轴交与A，B两点（点A在点B的左侧），与y轴交于点C．点D和点C关于抛物线的对称轴对称，直线AD与y轴相交于点E．‎ ‎（1）求直线AD的解析式；‎ ‎（2）如图1，直线AD上方的抛物线上有一点F，过点F作FG⊥AD于点G，作FH平行于x轴交直线AD于点H，求△FGH的周长的最大值；‎ ‎（3）点M是抛物线的顶点，点P是y轴上一点，点Q是坐标平面内一点，以A，M，P，Q为顶点的四边形是AM为边的矩形，若点T和点Q关于AM所在直线对称，求点T的坐标．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）求出A、D两点坐标，利用待定系数法即可解决问题．‎ ‎（2）首先证明△FHG是等腰直角三角形，构建二次函数利用函数性质解决问题即可．‎ ‎（3）分两种情形①如图2中，若AP为对角线，利用相似三角形性质求出点T坐标．②如图3中，若AQ为对角线，利用相似三角形性质即可解决问题．‎ ‎【解答】解：（1）∵抛物线y=﹣x2+2x+3与x轴交与A，B两点（点A在点B的左侧），与y轴交于点C，‎ ‎∴点A坐标（﹣1，0），点B坐标（3，0），点C坐标（0，3），‎ ‎∵抛物线对称轴x=1，D、C关于对称轴对称，‎ ‎∴点D坐标（2，3），设直线AD为y=kx+b．则解得；‎ ‎∴直线AD解析式为：y=x+1．‎ ‎（2）如图1中，‎ ‎∵OA=OE=1，‎ ‎∴∠EAO=45°，‎ ‎∵FH∥AB，‎ ‎∴∠FHA=∠EAO=45°，‎ ‎∵FG⊥AH，‎ ‎∴△FGH是等腰直角三角形，‎ 设点F坐标（m，﹣m2+2m+3），‎ ‎∴点H坐标（﹣m2+2m+2，﹣m2+2m+3），‎ ‎∴FH=﹣m2+m+2，‎ ‎∴△FGH的周长=（﹣m2+m+2）+2×（﹣m2+m+2）=﹣（1+）（m﹣）2+‎ ‎∴△FGH的周长最大值为．‎ ‎（3）①如图2中，若AP为对角线 作PS⊥对称轴于于S，对称轴与x轴的交点为R，‎ ‎∵∠PMS+∠MPS=90°，∠PMS+∠AMR=90°，‎ ‎∴∠MPS=∠AMR，∵∠PSM=∠MRA，‎ ‎∴△PMS∽△MAR可得=，‎ ‎∴=，‎ ‎∴SM=，‎ ‎∴点P坐标（0，）‎ 由点的平移可知Q（﹣2，）‎ 故Q点关于直线AM的对称点T为（0，﹣）．‎ ‎②如图3中，若AQ为对角线，‎ 作AR∥y轴，MR∥x轴，AS∥y轴，PS∥AB，‎ 同理可证△ARM∽△PSA，‎ ‎∴=，‎ ‎∴AS=‎ ‎∴点P坐标（0，﹣），‎ 由点的平移可知Q（2，），‎ 故Q点关于直线AM的对称点T为（0，）．‎