中考数学第一轮复习一次方程组 5页

‎2018年中考数学第一轮复习--- 一元一次方程与二元一次方程组 ‎【复习目标】‎ 1． 了解一元一次方程及二元一次方程（组）的有关概念，会解一元一次方程及二元一次方程组。‎ 2． 进一步掌握用一元一次方程及二元一次方程组解决实际问题。‎ ‎【复习回顾】‎ 考点一 一元一次方程 ‎1. 叫方程。 是方程的解。‎ ‎2.一元一次方程是指含有一个_______，并且未知数的最高次数是______次的整式方程.‎ ‎3.等式的基本性质一：等式两边同加（或同减）同一个数（或同一个整式），所得结果仍为________.‎ 等式的基本性质二：等式两边同乘（或同除）同一个数（或同一个整式），其中除数（或除式）不为零，所得结果仍为________.‎ ‎3.解一元一次方程的依据是________________.‎ ‎4.解一元一次方程的基本步骤是________________________________.‎ 例1．（2014•滨州，第19题）解方程：2﹣ = ‎ 例2．关于x的方程的解为正实数，则k的取值范围是 ‎ 巩固练习：‎ ‎1、已知2x+5y＝3，用含y的代数式表示x，则x=________；当y=1时，x=________.‎ ‎2、当k=_______时，方程5x－k=3x＋8的解是－2‎ ‎3、已知关于的方程的解是，则的值是______________。‎ ‎4、当 x 为何值时，代数式的值比的值大1.‎ ‎ 考点二 二元一次方程及二元一次方程组 ‎1.二元一次方程是指含有_______个未知数，并且_______的最高次数为_______次的整式方程.‎ ‎2. 二元一次方程组求解的基本思想是_________，常用方法有_________消元法和_________消元法.‎ 例1.（2014•孝感）已知是二元一次方程组的解，则m﹣n的值是（　　）‎ ‎　‎ A．‎ ‎1‎ B．‎ ‎2‎ C．‎ ‎3‎ D．‎ ‎4‎ 例2、若关于x，y的二元一次方程组的解也是二元一次方程 的解，则k的值为（ ） ‎ A. B. C. D. ‎ 例3.（2014•毕节地区）若﹣2amb4与5an+2b2m+n可以合并成一项，则mn的值是（ ）‎ ‎　‎ A．‎ ‎2‎ B．‎ ‎0‎ C．‎ ‎﹣1‎ D．‎ ‎1‎ 例4. 方程 2x＋y＝5 的所有正整数解为_________。‎ 例5.解方程组：（1） （2）‎ ‎ ‎ 巩固练习 ‎1、如果，求的值 ‎2、（2014•襄阳）若方程mx+ny=6的两个解是，，则m，n的值为（　　）‎ ‎　‎ A．‎ ‎4，2‎ B．‎ ‎2，4‎ C．‎ ‎﹣4，﹣2‎ D．‎ ‎﹣2，﹣4‎ ‎3、（2014·台湾）若二元一次联立方程式的解为x＝a，y＝b，则a＋b之值为何？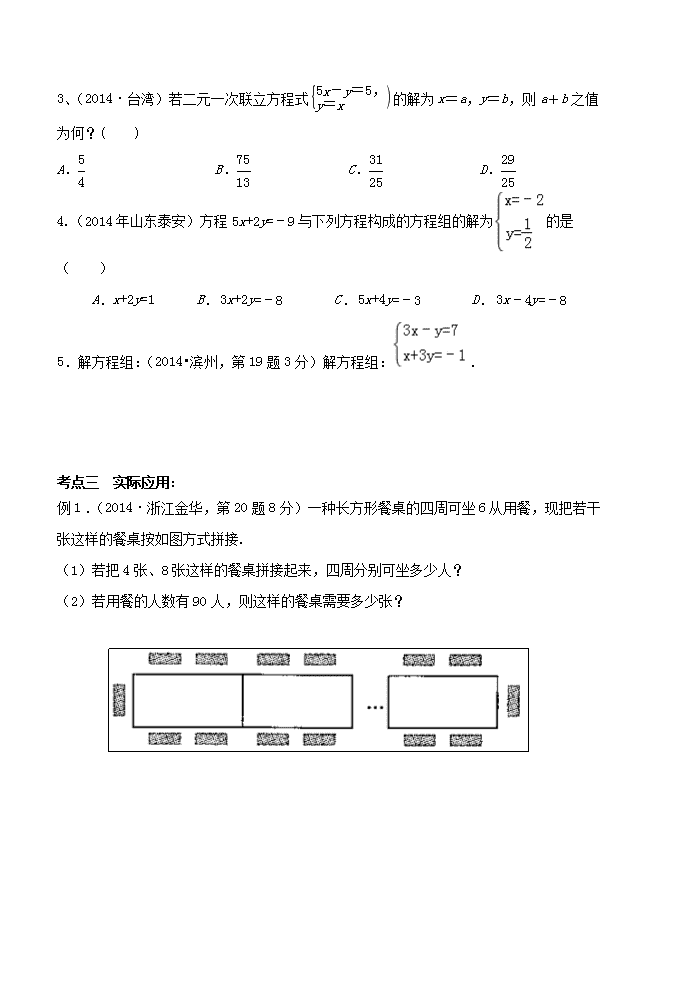(　　)‎ A． B． C． D． ‎4.（2014年山东泰安）方程5x+2y=﹣9与下列方程构成的方程组的解为的是（　　）‎ ‎　A．x+2y=1 B． 3x+2y=﹣8 C． 5x+4y=﹣3 D． 3x﹣4y=﹣8‎ ‎5．解方程组：（2014•滨州，第19题3分）解方程组：．‎ ‎ ‎ ‎ ‎ 考点三 实际应用：‎ 例1 ．（2014·浙江金华，第20题8分）一种长方形餐桌的四周可坐6 从用餐，现把若干张这样的餐桌按如图方式拼接.‎ ‎（1）若把4张、8张这样的餐桌拼接起来，四周分别可坐多少人？‎ ‎（2）若用餐的人数有90人，则这样的餐桌需要多少张？‎ ‎ ‎ 例2．（2014•泰州，第20题，8分）某篮球运动员去年共参加40场比赛，其中3分球的命中率为0.25，平均每场有12次3分球未投中．‎ ‎（1）该运动员去年的比赛中共投中多少个3分球？‎ ‎（2）在其中的一场比赛中，该运动员3分球共出手20次，小亮说，该运动员这场比赛中一定投中了5个3分球，你认为小亮的说法正确吗？请说明理由．‎ 巩固练习：‎ ‎1、一家商店将某件商品按成本价提高50%后，标价为450元，又以8折出售，则售出这件商品可获利润______元．‎ ‎3. （2014•泰州，第21题，10分）今年“五一”小长假期间，某市外来与外出旅游的总人数为226万人，分别比去年同期增长30%和20%，去年同期外来旅游比外出旅游的人数多20万人．求该市今年外来和外出旅游的人数．‎ ‎【作业】‎ ‎1.（2017年湖南省长沙市第14题）方程组的解是 ．‎ ‎2.（2017年湖北省荆州市第19题）（本题满分10分）（1）解方程组： ‎ ‎3.（2017年山东省东营市第23题）为解决中小学大班额问题，东营市各县区今年将改扩建部分中小学，某县计划对A、B两类学校进行改扩建，根据预算，改扩建2所A类学校和3所B类学校共需资金7800万元，改扩建3所A类学校和1所B类学校共需资金5400万元．‎ ‎（1）改扩建1所A类学校和1所B类学校所需资金分别是多少万元？‎ ‎（2）该县计划改扩建A、B两类学校共10所，改扩建资金由国家财政和地方财政共同承担．若国家财政拨付资金不超过11800万元；地方财政投入资金不少于4000万元，其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元．请问共有哪几种改扩建方案？‎