中考数学几何旋转例题 7页

旋转知识点归纳 O B A 图1‎ 知识点1:旋转的定义及其有关概念 在平面内，将一个图形绕一个定点O沿某个方向转动一个角度，这样的图形运动称为旋转，定点O称为旋转中心，转动的角称为旋转角;如果图形上的点P经过旋转到点,那么这两个点叫做这个旋转的对应点. 如图1,线段AB绕点O顺时针转动得到,这就是旋转,点O就是旋转中心,都是旋转角.‎ 说明: 旋转的范围是在平面内旋转，否则有可能旋转为立体图形，因此“在平面内”这一条件不可忽略.决定旋转的因素有三个:一是旋转中心;二是旋转角;三是旋转方向.‎ 知识点2:旋转的性质 由旋转的定义可知，旋转不改变图形的大小和形状，这说明旋转前后的两个图形是全等的.由此得到如下性质：‎ ‎⑴经过旋转，图形上的每一点都绕旋转中心沿相同方向转动了相同的角度，对应点的排列次序相同.‎ ‎⑵任意一对对应点与旋转中心的连线所成的角都是旋转角.‎ ‎⑶对应点到旋转中心的距离相等.‎ ‎⑷对应线段相等，对应角相等.‎ 图2‎ 例1 、如图2，D是等腰Rt△ABC内一点，BC是斜边，如果将△ADB绕点逆时针方向旋转到△的位置，则的度数是（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ 知识点3:旋转作图 例2 如图3，小明将△ABC绕O点旋转得到△，其中点分别是A、B、C的对应点.随即又将△ABC的边AC、BC及旋转中心O擦去(不留痕迹),他说他还能把旋转中心O及△ABC的位置找到,你认为可以吗?若可以,试确定旋转中心及的位置;如不可以,请说明理由.‎ 评注:旋转角相等及对应点到旋转中心的距离相等是解决这类问题的关键.‎ 图4‎ C B A O 图3‎ 考点4:钟表的旋转问题 钟表的时针与分针每时每刻都以轴心为旋转中心作旋转运动,其中时针12小时旋转一周,则每小时旋转这样时针每分钟旋转分针每小时旋转一周,则每分钟旋转 例3 从1点到1点25分,分针转了多少度角?时针转了多少度角?1点25分时时针与分针的夹角是多少度?‎ 解读生活中的旋转 ‎.‎ 五.典例剖析 图1‎ 例1如图1，是等腰内一点，是斜边，如果将绕点逆时针方向旋转到的位置，则的度数是（ 　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ 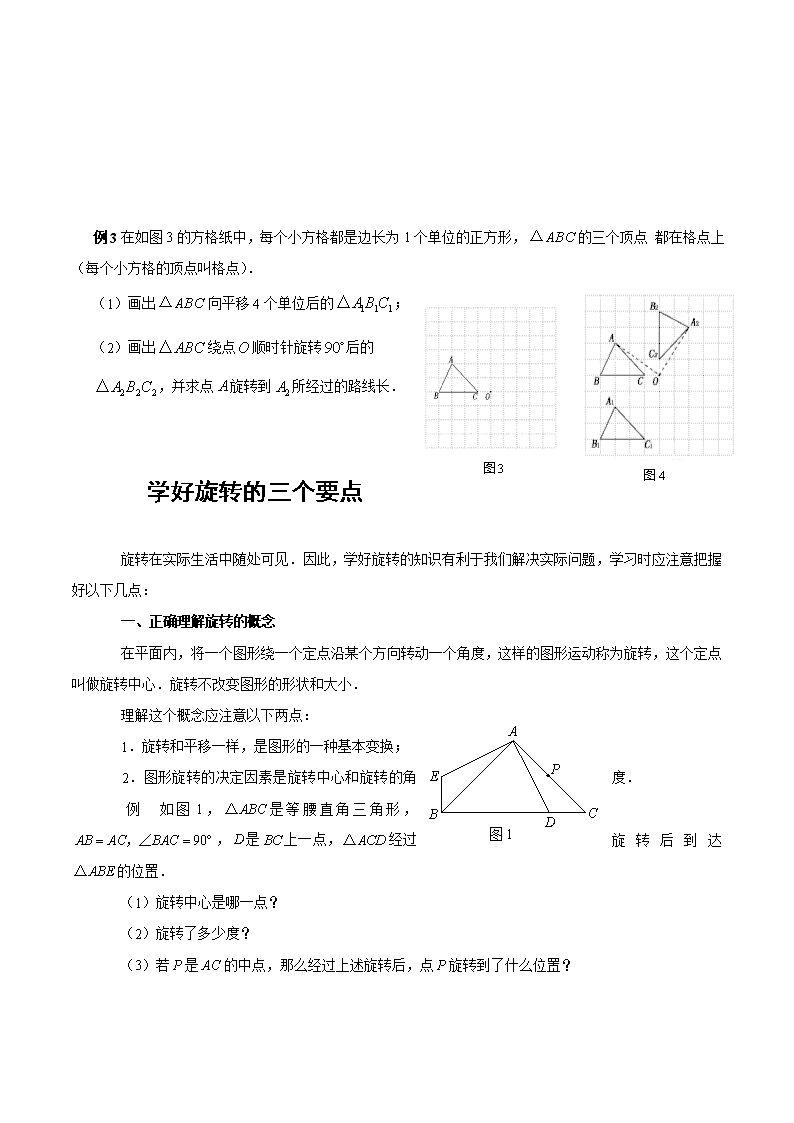例3在如图3的方格纸中，每个小方格都是边长为1个单位的正方形，的三个顶点 都在格点上（每个小方格的顶点叫格点）．‎ 图4‎ 图3‎ ‎（1）画出向平移4个单位后的；‎ ‎（2）画出绕点顺时针旋转后的 ‎，并求点旋转到所经过的路线长．‎ 学好旋转的三个要点 ‎　　旋转在实际生活中随处可见．因此，学好旋转的知识有利于我们解决实际问题，学习时应注意把握好以下几点：‎ ‎　　一、正确理解旋转的概念 ‎　　在平面内，将一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动称为旋转，这个定点叫做旋转中心．旋转不改变图形的形状和大小．‎ A C D B E P 图1‎ ‎　　理解这个概念应注意以下两点：‎ ‎　　1．旋转和平移一样，是图形的一种基本变换；‎ ‎　　2．图形旋转的决定因素是旋转中心和旋转的角度．‎ ‎　　例　如图1，是等腰直角三角形，，是上一点，经过旋转后到达的位置．‎ ‎　　（1）旋转中心是哪一点？‎ ‎　　（2）旋转了多少度？‎ ‎　　（3）若是的中点，那么经过上述旋转后，点旋转到了什么位置？‎ ‎　　‎ ‎　‎ ‎　　三、会寻找旋转中心 ‎　　‎ ‎　　例3　如图3所示，四边形绕某点旋转后到四边形，你能确定旋转中心吗?试一试．‎ ‎　　分析：我们可以用待定位置法．假定点就是旋转中心，由于对应点到旋转中心的距离相等，则有，从而一定是线段和线段的垂直平分线的交点上．‎ ‎　　．‎ 图1‎ 图4‎ ‎　　心．‎ ‎　　例2　如图4，是等边三角形，点分别是的中点，四边形和四边形都是正方形．‎ ‎　　（1）试确定正方形绕某点旋转得正方形的旋转中心．‎ ‎　　（2）正方形旋转多少度时可以与正方形重合？‎ ‎　　分析：因为四边形和四边形都是正方形，所以情况较多，我们只选择其中一个讲解，其它情况请同学们自己探索，欢迎你把自己的探索成果告诉我们．‎ ‎　　解：（1）选择和作为对应线段（点对应点，点的对应点为点）．‎ ‎　　连接，则易知，连接点与线段的中点并延长，连接点与线段的中点并延长，两直线相交于点，则有垂直平分垂直平分，则点就是旋转中心．为旋转角．‎ ‎　　（2），‎ ‎，‎ ‎　　（对顶角）．‎ ‎　　又，所以．‎ ‎　　所以旋转角．‎ ‎　　所以当正方形绕点顺时针旋转时，可与正方形重合．‎ 旋转坐标新意多 求旋转后点的坐标的问题是学习旋转是常见的问题。这类问题新意颇多，下面举例说明，供同学们学习时参考 ‎1、求旋转90°后点的坐标 例1、如图，在平面直角坐标系中，点A的坐标为(1，4)，将线段OA绕点O顺时针旋转90°得到线段OA′，则点A′的坐标是 ．‎ 分析：在平面直角坐标系中，先做出OA绕点O顺时针旋转90°后得到的线段OA′，然后根据点A′的特征求出点A′的坐标 解：如图所示，做出OA绕点O顺时针旋转90°后得到的线段OA′，则A′的坐标为(4，－1)‎ 规律总结：已知点的坐标为，为坐标原点，连结，将线段绕点按顺时针方向旋转90°得，则点的坐标为，将线段绕点按逆时针方向旋转90°得，则点的坐标为，‎ ‎2、求旋转180°后点的坐标 例2、在平面直角坐标系中，已知点A(2，3)，若将OA绕原点O逆时针旋转180°得到‎0A′，则点A′在平面直角坐标系中的位置是在 ‎ A 第一象限 B 第二象限 c 第三象限 D 第四象限 分析：将OA绕原点O逆时针旋转180°得到‎0A′，则点A′与点A关于原点成中心对称，根据点A的坐标即可求出点A′的坐标，从而确定A′在平面直角坐标系中的位置 规律总结：已知点的坐标为，为坐标原点，连结，将线段绕点 按顺时针方向（或逆时针方向）旋转180°得，则点的坐标为， ‎ ‎3、求旋转135°后点的坐标 例3、点A的坐标为（，0），把点A绕着坐标原点顺时针旋转135º到点B，那么点B的坐标是 _________ ．‎ 分析：如图所示，在平面直角坐标系中，小格点正方形的边长为1，在图中先通过旋转作图确定点B的位置，然后再求出它的坐标 ‎）‎ ‎4、求多次旋转后点的坐标 例4、如图，在直角坐标系中，已知点，，对△连续作旋转变换，依次得到三角形①、②、③、④…，则三角形⑩的直角顶点的坐标为________‎ 点评：解决本题的关键是找出△连续作旋转变换中三角形的直角顶点的坐标的变化规律，要求同学们具有一定的探索和想象能力。‎ 旋转常见错解剖析 ‎　　一、分析旋转作图时语言叙述不准确 ‎　　例1　分析图1的旋转现象.‎ ‎　　错解：本题是由图案的绕图案中心分别旋转 四次，每次旋转90°形成的.‎ ‎　　剖析：分析旋转图案的方法：（1）找准旋转图案 的基本图案，本题取图案的或；（2）找出旋　　　　　　图1‎ 转中心；（3）算准旋转的角度.‎ ‎　　正解：是由一个梯形绕图案中心依次旋转90°，180°，270°而形成的，也可以看做是由两个相邻的梯形绕图案的中心旋转180°而形成的.‎ ‎　　二、弄错图形的旋转方向 ‎　‎ ‎　　‎ ‎　　三、忽视分类讨论 ‎　　例3　在△ABC中，∠B=45°，∠C=60°，将△ABC绕点A旋转30°后与△AB‎1C1重合，求∠BAC1的度数.‎ ‎　　四、对旋转角的概念理解不准确 B E A C D 图6‎ ‎　　例4　如图6，P等边△BDE是由等边△ABC经过旋转得到的.试判断旋转中心和旋转角及旋转方向.‎ ‎　‎ ‎　　五、旋转作图中，找不准关键点，错用旋转的性质 ‎　　例5　如图7所示，请将方格纸中的图形以点O为旋转中心，顺时针旋转90°，再向左平移两格，你能作出相应的图形吗？‎ ‎　　‎ ‎　　剖析：未找准关键点关于旋转中心的对称点.‎ ‎　　‎ O O O 图7‎ 图8‎ 图9‎