中考数学必做36道压轴题合订本含变式训练 54页

‎2016中考必做的36道压轴题及变式训练 第1题 夯实双基“步步高”，强化条件是“路标”‎ ‎【例1】（2013北京，23,7分）在平面直角坐标系中，抛物线 与y轴交于点A，其对称轴与x轴交于点B．‎ ‎（1）求点A，B的坐标；‎ ‎（2）设直线与直线AB关于该抛物线的对称轴对称，求直线的解析式；‎ ‎ （3）若该抛物线在这一段位于直线的上方，并且在这一段位于直线AB的下方，求该抛物线的解析式．‎ 链接：（2013南京，26,9分）已知二次函数y=a(x-m)2-a(x-m) (a、m为常数，且a¹0)．‎ ‎ （1）求证：不论a与m为何值，该函数的图像与x轴总有两个公共点；‎ ‎ （2）设该函数的图象的顶点为C，与x轴交于A、B两点，与y轴交于点D．‎ ‎ ①当△ABC的面积等于1时，求a的值；‎ ‎ ②当△ABC的面积与△ABD的面积相等时，求m的值．‎ 变式：（2012北京，23,7分）已知二次函数在和时的函数值相等．‎ ‎（1）求二次函数的解析式；‎ ‎（2）若一次函数的图象与二次函数的图象都经过点A（-3，m），求m和k的值；‎ ‎（3）设二次函数的图象与x轴交于点B，C（点B在点C的左侧），将二次函数的图象在点B，C间的部分（含点B和点C）向左平移个单位后得到的图象记为G，同时将（2）中得到的直线向上平移n个单位．请结合图象回答：当平移后的直线与图象G有公共点时，n的取值范围．‎ 第2题 “弓形问题”再相逢，“殊途同归”快突破 ‎【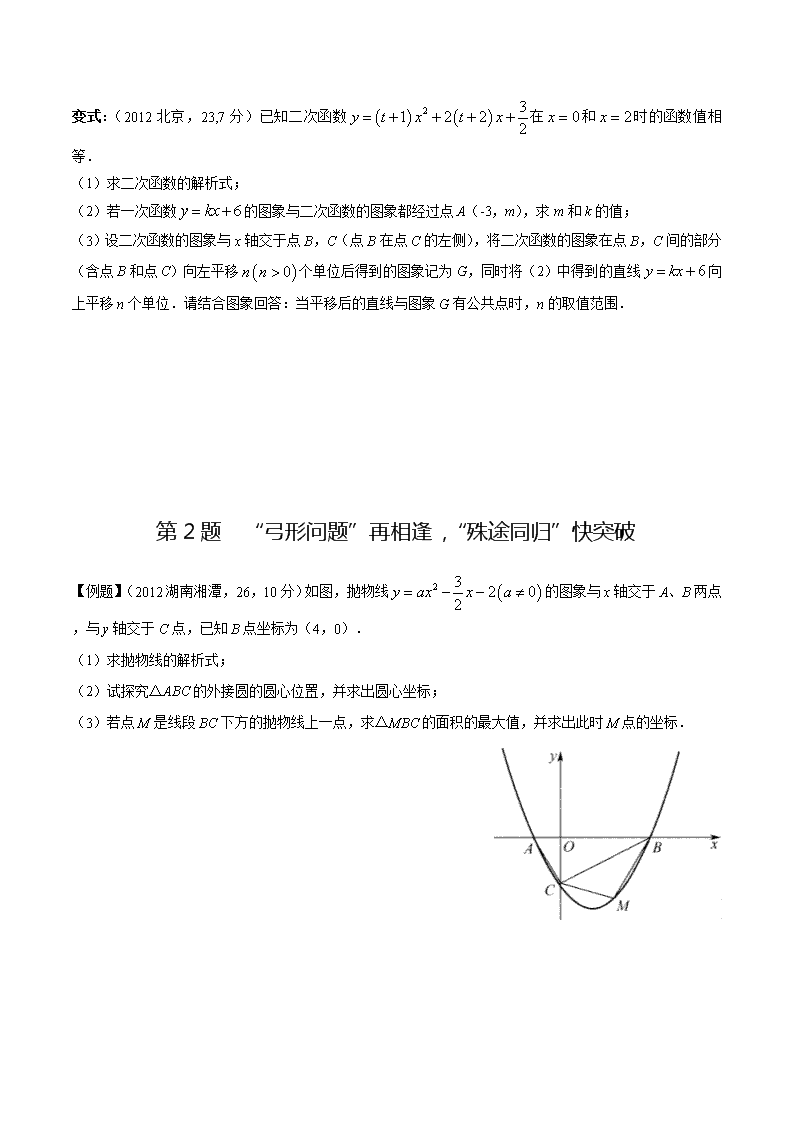例题】（2012湖南湘潭，26，10分）如图，抛物线的图象与x轴交于A、B两点，与y轴交于C点，已知B点坐标为（4，0）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）试探究△ABC的外接圆的圆心位置，并求出圆心坐标；]‎ ‎（3）若点M是线段BC下方的抛物线上一点，求△MBC的面积的最大值，并求出此时M点的坐标．‎ ‎【变式】（2011安徽芜湖，24，14分）平面直角坐标系中，如图放置，点A、C的坐标分别为（0，3）、（﹣1，0），将此平行四边形绕点O顺时针旋转90°，得到．‎ ‎（1）若抛物线过点C，A，A'，求此抛物线的解析式；‎ ‎（2）和重叠部分△OC'D的周长；‎ ‎（3）点M是第一象限内抛物线上的一动点，问：点M在何处时△AMA'的面积最大？最大面积是多少？并求出此时M的坐标．‎ 第3题 “模式识别”记心头，看似“并列”实“递进”‎ ‎【例题】（2012河南，23，11分）如图，在平面直角坐标系中，直线与抛物线交于A，B两点，点A在轴上，点B的纵坐标为3．点P是直线AB下方的抛物线上一动点（不与A，B重合），过点P作轴的垂线交直线AB与点C，作PD⊥AB于点D．‎ ‎（1）求a，b及的值；‎ ‎（2）设点P的横坐标为．‎ ‎ ①用含的代数式表示线段PD的长，并求出线段PD长的最大值；‎ ‎ ②连接PB，线段PC把分成两个三角形，是否存在适合的值，使这两个三角形的面积之比为9:10？若存在，直接写出值；若不存在，说明理由．‎ ‎【变式一】（2011江苏泰州，27，12分）已知：二次函数的图象经过点P（﹣2，5）．‎ ‎（1）求b的值并写出当时y的取值范围；‎ ‎（2）设（m，）、（m+1，）、（m+2，）在这个二次函数的图象上．‎ ‎ ①当m=4时，、、能否作为同一个三角形三边的长？请说明理由；‎ ‎ ②当m取不小于5的任意实数时，、、一定能作为同一个三角形三边的长，请说明理由．‎ ‎【变式二】（2013重庆，25题，12分）如图，已知抛物线的图象与x轴的一个交点为B（5，0），另一个交点为A，且与y轴交于点C（0，5）．‎ ‎（1）求直线BC与抛物线的解析式；‎ ‎（2）若点M是抛物线在x轴下方图象上的一动点，过点M作MN∥y轴交直线BC于点N，求MN的最大值；‎ ‎（3）在（2）的条件下，MN取得最大值时，若点P是抛物线在x轴下方图象上任意一点，以BC为边作平行四边形CBPQ，设平行四边形CBPQ的面积为，△ABN的面积为，且，求点P的坐标．‎ 第4题 “准线”“焦点”频现身，“居高临下”明“结构”‎ ‎【例题】（2012四川资阳，25，9分）抛物线的顶点在直线上，过点F（－2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．‎ （1） 先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；‎ （2） 设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF＝NB；‎ ‎（3）若射线NM交x轴于点P，且PA×PB＝，求点M的坐标．‎ ‎【变式一】（2010湖北黄冈，25，15分）已知抛物线顶点为C（1，1）且过原点O．过抛物线上一点P（x，y）向直线作垂线，垂足为M，连FM（如图）．‎ ‎（1）求字母a，b，c的值；‎ ‎（2）在直线x=1上有一点F（1，），求以PM为底边的等腰三角形PFM的P点的坐标，并证明此时△PFM为正三角形；‎ ‎（3）对抛物线上任意一点P，是否总存在一点N（1，t），使PM=PN恒成立？若存在请求出t值，若不存在请说明理由．‎ ‎【变式二】（2012山东潍坊，24,11分）如图，已知抛物线与坐标轴分别交于A(－2，0)、B(2，0)、C(0，－1)三点，过坐标原点O的直线与抛物线交于M、N两点．分别过点C、D(0，－2)作平行于x轴的直线、．‎ ‎（1）求抛物线对应二次函数的解析式；‎ ‎（2）求证以ON为直径的圆与直线相切；‎ ‎（3）求线段MN的长(用k表示)，并证明M、N两点到直线的距离之和等于线段MN的长．‎ 第5题 莫为“浮云”遮望眼，“洞幽察微”探指向 ‎【例题】（2012浙江宁波，26，12分）如图，二次函数y=ax2+bx+c的图象交x轴于A（﹣1，0），B（2，0），交y轴于C（0，﹣2），过A，C画直线．‎ ‎（1）求二次函数的解析式；‎ ‎（2）点P在x轴正半轴上，且PA=PC，求OP的长；‎ ‎（3）点M在二次函数图象上，以M为圆心的圆与直线AC相切，切点为H．‎ ‎ ①若M在y轴右侧，且△CHM∽△AOC（点C与点A对应），求点M的坐标；‎ ‎ ②若⊙M的半径为，求点M的坐标．‎ ‎【变式一】（2010湖南邵阳，25，12分）如图，抛物线与x轴相交于点A、B，与y轴相交于点C，顶点为点D，对称轴l与直线BC相交于点E，与x轴相交于点F．‎ ‎（1）求直线BC的解析式；‎ ‎（2）设点P为该抛物线上的一个动点，以点P为圆心，r为半径作⊙P．‎ ‎ ①当点P运动到点D时，若⊙P与直线BC相交，求r的取值范围；‎ ‎ ②若，是否存在点P使⊙P与直线BC相切？若存在，请求出点P的坐标；若不存在，请说明理由．‎ ‎【变式二】（2012广东省，22，9分）如图，抛物线与x轴交于A、B两点，与y轴交于点C，连接BC、AC．‎ ‎（1）求AB和OC的长；‎ ‎（2）点E从点A出发，沿x轴向点B运动（点E与点A、B不重合），过点E作直线l平行BC，交AC于点D．设AE的长为m，△ADE的面积为S，求S关于m的函数关系式，并写出自变量m的取值范围；‎ ‎（3）在（2）的条件下，连接CE，求△CDE面积的最大值；此时，求出以点E为圆心，与BC相切的圆的面积（结果保留π）．‎ 第6题 分类讨论“程序化”，“分离抗扰”探本质 ‎【例题】（2011贵州遵义，27，14分）已知抛物线y=ax2+bx+3（a≠0）经过A（3，0），B（4，1）两点，且与y轴交于点C．‎ ‎（1）求抛物线y=ax2+bx+3（a≠0）的函数关系式及点C的坐标；‎ ‎（2）如图（1），连接AB，在题（1）中的抛物线上是否存在点P，使△PAB是以AB为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；‎ ‎（3）如图（2），连接AC，E为线段AC上任意一点（不与A、C重合）经过A、E、O三点的圆交直线AB于点F，当△OEF的面积取得最小值时，求点E的坐标．‎ ‎【变式一】（2012山东枣庄，25，10分）在平面直角坐标系中，现将一块等腰直角三角板ABC斜靠在两坐标轴上放在第二象限，斜靠在两坐标轴上，点C为（﹣1，0）．B点在抛物线图象上，过点B作BD⊥x轴，垂足为D，且B点横坐标为﹣3．‎ ‎（1）求证：△BDC≌△COA；‎ ‎（2）求BC所在直线的函数关系式；‎ ‎（3）抛物线的对称轴上是否存在点P，使△ACP是以AC为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．‎ ‎【变式二】（2011四川南充，21，8分）如图，等腰梯形ABCD中，AD∥BC，AD=AB=CD=2，∠C=60°，M是BC的中点．‎ ‎（1）求证：△MDC是等边三角形；‎ ‎（2）将△MDC绕点M旋转，当MD（即MD′）与AB交于一点E，MC（即MC′）同时与AD交于一点F时，点E，F和点A构成△AEF．试探究△AEF的周长是否存在最小值？如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值．‎ 第7题 “两种对称”正方形，“以美启真”助破题 ‎【例题】（2013浙江杭州，23,12分）如图，已知正方形ABCD的边长为4，对称中心为点P，点F为BC边上一个动点，点E在AB边上，且满足条件∠EPF=45°，图中两块阴影部分图形关于直线AC成轴对称，设它们的面积和为S1．‎ ‎（1）求证：∠APE=∠CFP；‎ ‎（2）设四边形CMPF的面积为S2，CF=x，．‎ ‎ ①求y关于x的函数解析式和自变量x的取值范围，并求出y的最大值；‎ ‎ ②当图中两块阴影部分图形关于点P成中心对称时，求y的值．‎ ‎【变式一】（2013湖南娄底，23,9分）某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．‎ ‎（1）求证：AM=AN；‎ ‎（2）当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．‎ ‎【变式二】（2013北京海淀区九上期末卷）如图1，两个等腰直角三角板ABC和DEF有一条边在同一条直线l上，DE=2，AB=1．将直线EB绕点E逆时针旋转45°，交直线AD于点M．将图1中的三角板ABC沿直线l向右平移，设C、E两点间的距离为k．‎ 解答问题：‎ （1） ‎①当点C与点F重合时，如图2所示，可得的值为　 　；②在平移过程中，的值为　 　（用含k的代数式表示）；‎ （2） 将图2中的三角板ABC绕点C逆时针旋转，原题中的其他条件保持不变．当点A落在线段DF上时，如图3所示，请补全图形，计算的值；‎ ‎（3）将图1中的三角板ABC绕点C逆时针旋转α度，0＜α≤90，原题中的其他条件保持不变．计算的值（用含k的代数式表示）．‎ 第8题 对称图形为载体，特殊位置要留意 ‎【例题】（2013四川资阳，24，12分）如图，四边形ABCD是平行四边形，过点A、C、D作抛物线，与x轴的另一交点为E，连结CE，点A、B、D的坐标分别为（-2，0）、（3，0）、（0，4）.‎ ‎（1）求抛物线的解析式；‎ ‎（2）已知抛物线的对称轴l交x轴于点F，交线段CD于点K，点M、N分别是直线l和x轴上的动点，连结MN，当线段MN恰好被BC垂直平分时，求点N的坐标；‎ ‎（3）在满足（2）的条件下，过点M作一条直线，使之将四边形AECD的面积分为3∶4的两部分，求出该直线的解析式.‎ ‎【变式一】（2011江苏无锡，27，10分）如图，已知O(0，0)、A(4，0)、B(4，3)．动点P从O点出发，以每秒3个单位的速度，沿△OAB的边OA、AB、BO作匀速运动；动直线l从AB位置出发，以每秒1个单位的速度向x轴负方向作匀速平移运动．若它们同时出发，运动的时间为t秒，当点P运动到O时，它们都停止运动．‎ ‎ （1）当P在线段OA上运动时，求直线l与以点P为圆心、1为半径的圆相交时t的取值范围；‎ ‎ （2）当P在线段AB上运动时，设直线l分别与OA、OB交于C、D，试问：四边形CPBD是否可能为菱形？若能，求出此时t的值；若不能，请说明理由，并说明如何改变直线l的出发时间，使得四边形CPBD会是菱形．‎ 第9题 平行线内“正方形”，构造全等“弦方图”‎ ‎【例题】（2012山东滨州，25,12分）如图1，，，，是一组平行线，相邻2条平行线间的距离都是1个单位长度，正方形ABCD的4个顶点A，B，C，D都在这些平行线上．过点A作AF⊥于点F，交于点H，过点C作CE⊥于点E，交于点G．‎ ‎（1）求证：△ADF ≌△CBE；‎ ‎（2）求正方形ABCD的面积；‎ ‎（3）如图2，如果四条平行线不等距，相邻的两条平行线间的距离依次为，，，试用，，表示正方形ABCD的面积S．‎ ‎【变式一】（2013山东淄博，24，9分）矩形纸片ABCD中，AB=5，AD=4．‎ ‎（1）如图1，四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形．你能否在该矩形中裁剪出一个面积最大的正方形，最大面积是多少？说明理由；‎ ‎（2）请用矩形纸片ABCD剪拼成一个面积最大的正方形．要求：在图2的矩形ABCD中画出裁剪线，并在网格中画出用裁剪出的纸片拼成的正方形示意图（使正方形的顶点都在网格的格点上）．‎ ‎【变式二】（2011安徽，23，14分）如图，正方形ABCD的四个顶点分别在四条平行线上.这四条直线中相邻两条之间的距离依次为（，，）.‎ ‎（1）求证：；‎ ‎（2）设正方形ABCD的面积为，求证：；‎ ‎（3）若，当变化时，说明正方形的面积随变化的情况.‎ 第10题 “并列”问题“递进”解，经典问题再追问 ‎【例题】（2012山东德州，23，12分）如图所示，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点（不与点A、点D重合）将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH．‎ ‎（1）求证：∠APB=∠BPH；‎ ‎（2）当点P在边AD上移动时，△PDH的周长是否发生变化？并证明你的结论；‎ ‎（3）设AP为x，四边形EFGP的面积为S，求出S与x的函数关系式，试问S是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．‎ ‎【变式】（2013辽宁锦州，25，12分）如图1，等腰直角三角板的一个锐角顶点与正方形 ABCD的顶点A重合，将此三角板绕点A旋转，使三角板中该锐角的两条边分别交正方形 的两边BC、DC于点E、F，连结EF．‎ ‎（1）猜想BE、EF、DF三条线段之间的数量关系，并证明你的猜想；‎ ‎（2）在图1中，过点A作AM⊥EF于点M，请直接写出AM和AB的数量关系；‎ ‎（3）如图2，将Rt△ABC沿斜边AC翻折得到Rt△ADC，E、F分别是BC、CD边上的点，∠EAF＝∠BAD，连结EF，过点A作AM⊥EF于点M．试猜想AM与AB之间的数量关系，并证明你的猜想．‎ 第11题 “伴随图形”来研究，“分类讨论”显功底 ‎【例题】（2011辽宁本溪，26，14分）如图1，在平面直角坐标系中，抛物线过原点O，点A（10，0）和点B（2，2），在线段OA上，点P从点O向点A运动，同时点Q从点A向点O运动，运动过程中保持AQ=2OP，当P、Q重合时同时停止运动，过点Q作x轴的垂线，交直线AB于点M，延长QM到点D，使MD=MQ，以QD为对角线作正方形QCDE（正方形QCDE岁点Q运动）．‎ ‎（1）求这条抛物线的函数表达式；‎ ‎（2）设正方形QCDE的面积为S，P点坐标（m，0）求S与m之间的函数关系式；‎ ‎（3）过点P作x轴的垂线，交抛物线于点N，延长PN到点G，使NG=PN，以PG为对角线作正方形PFGH（正方形PFGH随点P运动），当点P运动到点（2，0）时，如图2，正方形PFGH的边GP和正方形QCDE 的边EQ落在同一条直线上．‎ ‎①则此时两个正方形中在直线AB下方的阴影部分面积的和是多少？‎ ‎②若点P继续向点A运动，还存在两个正方形分别有边落在同一条直线上的情况，请直接写出每种情况下点P的坐标，不必说明理由．‎ ‎【变式】（2013湖南郴州，25，10分）如图，△ABC中，AB=BC，AC=8，tan A=k，P为AC边上一动点，设PC=x，作PE∥AB交BC于E，PF∥BC交AB于F．‎ ‎（1）证明：△PCE是等腰三角形；‎ ‎（2）EM、FN、BH分别是△PEC、△AFP、△ABC的高，用含x和k的代数式表示EM、FN，并探究EM、FN、BH之间的数量关系；‎ ‎（3）当k=4时，求四边形PEBF的面积S与x的函数关系式．x为何值时，S有最大值？并求出S的最大值．‎ 第12题 中心对称“带上路”，以美启真构菱形 ‎【例题】（2013陕西，25，12分）‎ ‎ 问题探究 ‎（1）请在图①中作出两条直线，使它们将圆面四等分；‎ ‎（2）如图②，M是正方形ABCD内一定点，请在图②中作出两条直线（要求其中一条直线必须过点M），使它们将正方形ABCD的面积四等分，并说明理由.‎ ‎ 问题解决 ‎（3）如图③，在四边形ABCD中，AB∥CD，AB+CD=BC，点P是AD的中点，如果AB=，CD=，且，那么在边BC上是否存在一点Q，使PQ所在直线将四边形ABCD的面积分成相等的两部分？若存在，求出BQ的长；若不存在，说明理由.‎ ‎【变式一】（2012陕西，25，12分）如图，正三角形ABC的边长为．‎ ‎（1）如图①，正方形EFPN的顶点E、F在边AB上，顶点N在边AC上．在正三角形ABC及其内部，以A为位似中心，作正方形EFPN的位似正方形，且使正方形的面积最大（不要求写作法）；‎ ‎（2）求（1）中作出的正方形的边长；‎ ‎（3）如图②，在正三角形ABC中放入正方形DEMN和正方形EFPH，使得D、EF在边AB上，点P、N分别在边CB、CA上，求这两个正方形面积和的最大值及最小值，并说明理由．‎ ‎【变式二】（2011湖北武汉，24，10分）‎ （1） 如图，在△ABC中，点D、E、Q分别在AB、AC、BC上，且DE∥BC边长，AQ交DE于点P．求证：=；‎ ‎（2）如图2，△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG，AF分别交DE于M，N两点．‎ ‎ ①如图2，若AB=AC=1，直接写出MN的长；‎ ‎ ②如图3，求证：．‎ 第13题 “定义”悟出基本图，解后反思“圆外圆”‎ ‎【例题】（2013北京，25，8分）对于平面直角坐标系中的点P和⊙C，给出如下定义：‎ 若⊙C上存在两个点A，B，使得∠APB=60°，则称P为⊙C 的关联点．‎ 已知点，E（0，-2），F（，0）．‎ ‎（1）当⊙O的半径为1时，‎ ‎ ①在点D，E，F中，⊙O的关联点是__________；‎ ‎ ②过点F作直线交轴正半轴于点G，使∠GFO=30°，若直线上的点（，）是⊙O的关联点，求的取值范围；‎ （2） 若线段EF上的所有点都是某个圆的关联点，求这个圆的半径的取值范．‎ ‎【变式一】（2013福建泉州，25，12分）如图，直线分别与x、y轴交于点B、C，点A(-2，0)，P是直线BC上的动点．‎ ‎（1）求∠ABC的大小；‎ ‎（2）求点P的坐标，使∠APO=30°；‎ ‎（3）在坐标平面内，平移直线BC，试探索：当BC在不同位置时，使∠APO = 30°的点P的个数是否保持不变？若不变，指出点 P的个数有几个？若改变，指出点 P的个数情况，并简要说明理由．‎ ‎【变式二】（2012江苏南京，27，10分）如图，A、B为⊙O上的两个定点，P是⊙O上的动点（P不与A、B重合），我们称∠APB为⊙O上关于A、B的滑动角．‎ ‎（1）已知∠APB是上关于点A、B的滑动角．‎ ‎ ① 若AB为⊙O的直径，则∠APB= ；‎ ‎ ② 若⊙O半径为1，AB=，求∠APB的度数．‎ ‎（2）已知为外一点，以为圆心作一个圆与相交于A、B两点，∠APB为上关于点A、B的滑动角，直线PA、PB分别交于点M、N（点M与点A、点N与点B均不重合），连接AN ‎，试探索∠APB与∠MAN、∠ANB之间的数量关系．‎ 第14题 “旋转变换”迷人眼，“见微知著”深追问 ‎【例题】（2012浙江义乌，23，10分）在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1．‎ （1） 如图，当点C1在线段CA的延长线上时，求∠CC1A1的度数；‎ （2） 如图2，连接AA1，CC1．若△ABA1的面积为4，求△CBC1的面积；‎ ‎（3）如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1，求线段EP1长度的最大值与最小值．‎ ‎【变式一】（2011安徽，22，12分）在△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋转角为(0°＜＜180°)，得到△A1B1C．‎ A A1‎ A C C C A1‎ A1‎ A D B1‎ B B B B1‎ B1‎ E P 图1‎ 图2‎ 图3‎ ‎（1）如图1，当AB∥CB1时，设A1B1与BC相交于点D．证明：△A1CD是等边三角形；‎ ‎【证】‎ ‎（2）如图2，连接AA1、BB1，设△ACA1和△BCB1的面积分别为S1、S2．求证：S1∶S2＝1∶3；‎ ‎【证】‎ ‎（3）如图3，设AC的中点为E，A1B1的中点为P，AC＝a，连接EP．当＝ °时，EP的长度最大，最大值为 ．‎ ‎【变式二】（原创题）如图，边长为2的正方形ABCD中，对角线AC、BD相交于点O，以D为圆心，DB的长为半径作弧交CA延长线于E，连接DE、BE．‎ （1） 求证：△BDE是等边三角形；‎ （2） 以点D为中心，把△CDE顺时针旋转角（）得到△．‎ ‎①当时，连接，求的值；‎ ‎②当、AB所在直线夹角为15°时，求所有可能的度数；‎ ‎③若点P是边上任意一点，在旋转过程中，试探究BP有没有最大（小）值？如果有，直接写出最大（小）值；如果没有，说明理由．‎ 第15题 构造全等获突破，道是“无圆”却“有圆”‎ ‎【例题】（2012青海，27题，10分）如图1，四边形ABCD是正方形，点E是边BC的中点，‎ ‎∠AEF=90°，且EF交正方形外角平分线CF于点F． 请你认真阅读下面关于这个图的探究 片段，完成所提出的问题．‎ ‎ 探究1：小强看到图1后，很快发现AE=EF．这需要证明AE和EF所在的两个三角形 ‎ 全等，但△ABE和△ECF显然不全等（一个直角三角形，一个钝角三角形）．考虑到点E 是边BC的中点，因此可以选取AB的中点M，连接EM后尝试着去证明△AEM≌△EFC 就行了．随即小强写出了如下的证明过程：‎ ‎ 证明：如图2，取AB的中点M，连接EM．‎ ‎∵∠AEF=90°，∴∠FEC+∠AEB=90°，‎ 又∵∠EAM+∠AEB=90°，∴∠EAM=∠FEC．∵点E、M分别为正方形的边BC和AB的中点，‎ ‎∴AM=EC．∵△BME是等腰直角三角形，∴∠AME=135°，又∵CF是正方形外角的平分线，‎ ‎∴∠ECF=135°，∴△AEM≌△EFC（ASA）,∴AE=EF．‎ ‎（2）探究2：小强继续探索，如图3，若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”，其余条件不变，发现AE=EF仍然成立．请你证明这一结论．‎ ‎ ‎ （3） 探究3：小强进一步还想试试，如图4，若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”，其余条件不变，那么结论AE=EF是否成立呢？若成立请你完成证明过程给小强看．若不成立请你说明理由．‎ ‎ ‎ ‎【变式一】（2013浙江湖州，24题，14分）如图1，已知正方形OABC的边长为2，顶点A、C分别在x、y轴的正半轴上，M是BC的中点．P（0，m）是线段OC上一动点（C点除外），直线PM交AB的延长线于点D．‎ ‎（1）求点D的坐标（用含m的代数式表示）；‎ ‎（2）当△APD是等腰三角形时，求m的值；‎ ‎（3）设过P、M、B三点的抛物线与x轴正半轴交于点E，过点O作直线ME的垂线，垂足为H（如图2），当点P从点O向点C运动时，点H也随之运动．请直接写出点H所经过的路径长．（不必写解答过程）‎ ‎【变式二】（2013内蒙古呼和浩特，23题，9分）如图，在边长为3的正方形ABCD中，点E是BC边上的点，BE=1，∠AEP=90°，且EP交正方形外角的平分线CP于点P，交边CD于点F，‎ ‎（1）的值为　 　；‎ ‎（2）求证：AE=EP；‎ ‎（3）在AB边上是否存在点M，使得四边形DMEP是平行四边形？若存在，请给予证明；若不存在，请说明理由．‎ 第16题 精确草图获思路，勾股相似构方程 ‎【例题】（2013上海，25题，10分）在矩形中，点是边上的动点，连接，线段的垂直平分线交边于点，垂足为点，连接（如图1）．已知，，设，．‎ ‎（1）求关于的函数解析式，并写出的取值范围；‎ ‎（2）当以长为半径的⊙P和以长为半径的⊙Q外切时，求的值；‎ ‎（3）点在边上，过点作直线的垂线，垂足为，如果，求的值．‎ ‎【变式一】（改编题）在△ABC中，AB=AC，AD是BC边上的高，点O在线段AD上．‎ （1） 如图1，连接OB、OC，求证：△BDO≌△CDO；‎ （2） 已知与直线AB、AC都相切，切点分别为E、F，当AD=12，CD=5，时，求证：与直线BC相切．‎ ‎【变式二】已知：如图1，直角坐标系内的矩形ABCD，顶点A的坐标为（0，3），BC=2AB，P为AD边上一动点（与点A、D不重合），以点P为圆心作与对角线AC相切于点F，过P、F作直线，交BC边于点E． 当点P运动到点位置时，直线恰好经过点B，此时直线的解析式是．‎ （1） 求BC、的长；‎ （2） 设AP=m，梯形PECD的面积为S，求S与m之间的函数关系式，写出自变量m的取值范围；‎ （3） 以点E为圆心作与x轴相切． 探究并猜想：和有哪几种不同的位置关系？并求出AP相应的取值范围．‎ 第17题 “正笔侧锋”细解读，“拨云见日”明“指向 ‎【例题】（2012广东广州，24题，14分）如图，抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．‎ ‎（1）求点A、B的坐标；‎ ‎（2）设点D为已知抛物线的对称轴上的任意一点，当△ACD的面积等于△ACB的面积时，求点D的坐标；‎ ‎（3）若直线l过点E（4，0），M为直线l上的动点，当以A、B、M为顶点所作的直角三角形有且只有三个时，求直线l的解析式．‎ ‎【变式一】（2013山东淄博，23题，9分）△ABC是等边三角形，点A与点D的坐标分别是A（4，0），D（10，0）．‎ （1） 如图1，当点C与点O重合时，求直线BD的解析式；‎ （2） 如图2，点C从点O沿y轴向下移动，当以点B为圆心，AB为半径的⊙B与y轴相切（切点为C）时，求点B的坐标；‎ ‎（3）如图3，点C从点O沿y轴向下移动，当点C的坐标为C（0，）时，求∠ODB的正切值．‎ ‎【变式二】（原创）如图，在平面直角坐标系中，矩形ABCD的边BC平行于x轴，AB=6，点A的横坐标为2，反比例函数的图象经过点A、C.‎ （1） 求点A的坐标；‎ （2） 求点B、D所在直线的函数关系式；‎ （3） 若点P（p，），是否存在实数p，使得？若存在，请直接写出所有满足条件的p的值；若不存在，请说明理由.‎ 第18题 “圆的折叠”来探究，发现“等圆”能破题 ‎【例题】（2012江西南昌，28题，12分）已知，纸片⊙O的半径为2，如图1，沿弦AB折叠操作．‎ ‎（1）①折叠后的所在圆的圆心为O′ 时，求O′A的长度；‎ ‎ ②如图2，当折叠后的经过圆心为O时，求的长度；‎ ‎ ③如图3，当弦AB=2时，求圆心O到弦AB的距离；‎ ‎（2）在图1中，再将纸片⊙O沿弦CD折叠操作．‎ ‎ ①如图4，当AB∥CD，折叠后的与所在圆外切于点P时，设点O到弦AB、CD的距离之和为d，求d的值；‎ ‎ ②如图5，当AB与CD不平行，折叠后的与所在圆外切于点P时，设点M为AB的中点，点N为CD的中点，试探究四边形OMPN的形状，并证明你的结论．‎ ‎【变式】（2011湖南常德，25题，10分）已知△ABC，分别以AC和BC为直径作半圆，P是AB的中点．‎ （1） 如图，若△ABC是等腰三角形，且AC=BC，在上分别取点E、F，使，则有结论①.②四边形是菱形．请给出结论②的证明；‎ （2） 如图，若（1）中△ABC是任意三角形，其它条件不变，则（1）中的两个结论还成立吗？若成立，请给出证明；‎ ‎（3）如图，若PC是⊙的切线，求证：．‎ 第19题 “强化条件”要看清，思路生成有“源头”‎ ‎【例题】（2011上海，25题，14分）在Rt△ABC中，∠ACB＝90°，BC＝30，AB＝50．点P是AB边上任意一点，直线PE⊥AB，与边AC或BC相交于E．点M在线段AP上，点N在线段BP上，EM＝EN，．‎ ‎（1）如图1，当点E与点C重合时，求CM的长；‎ ‎（2）如图2，当点E在边AC上时，点E不与点A、C重合，设AP＝x，BN＝y，求y关于x的函数关系式，并写出函数的定义域；‎ ‎（3）若△AME∽△ENB（△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应），求AP的长．‎ ‎【变式一】（2012安徽，22题，12分）如图1，在△ABC中，D、E、F分别为三边的中点，G点在边AB上，△BDG与四边形ACDG的周长相等，设BC=a、AC=b、AB=c.‎ ‎（1）求线段BG的长；‎ ‎（2）求证：DG平分∠EDF;‎ ‎（3）连接CG，如图2，若△BDG与△DFG相似，求证：BG⊥CG.‎ ‎【变式二】（2012上海，24题，12分）如图，在平面直角坐标系中，二次函数y=ax2+6x+c的图象经过点A（4，0）、B（﹣1，0），与y轴交于点C，点D在线段OC上，OD=t，点E在第二象限，∠ADE=90°，tan∠DAE=，EF⊥OD，垂足为F．‎ ‎（1）求这个二次函数的解析式；‎ ‎（2）求线段EF、OF的长（用含t的代数式表示）；‎ ‎（3）当∠ECA=∠OAC时，求t的值．‎ 第20题 “相似”与“∽”有区别，“参数运算”需细心 ‎【例题】（2012湖北黄冈，25题，14分）如图，已知抛物线与x轴相交于点B、C，与y轴相交于E，且点B在点C的左侧．‎ （1） 若抛物线过点M（2，2），求实数m的值；‎ （2） 在（1）的条件下，求△BCE的面积；‎ （1） 在（1）条件下，在抛物线的对称轴上找一点H，使得BH+EH最小，并求出点H的坐标；‎ （2） 在第四象限内，抛物线上是否存在点F，使得以点B、C、F为顶点的三角形与△BCE相似？若存在，求m的值；若不存在，请说明理由．‎ ‎【变式一】（2013湖南永州，25题，10分）如图，已知AB⊥BD，CD⊥BD．‎ ‎(1)若AB=9，CD=4，BD=10，请问在BD上是否存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似？若存在，求BP的长；若不存在，请说明理由；‎ ‎(2) 若AB=9，CD=4，BD=12，请问在BD上存在多少个P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似？并求BP的长；‎ ‎(3) 若AB=9，CD=4，BD=15，请问在BD上存在多少个P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似？并求BP的长；‎ ‎(4) 若AB=m，CD=n，BD=，请问在m、n、满足什么关系时，存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个P点? 两个P点? 三个P点?‎ ‎【变式二】（2011山东临沂，26题，13分）如图，已知抛物线经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若点D在抛物线上，点E在抛物线的对称轴上，且A、O、D、E为顶点的四边形是平行四边形，求点D的坐标；‎ ‎（3）P是抛物线上的第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P、M、A 为顶点的三角形△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．‎ 第21题 “角的等量”来探究，“把水倒掉”巧构造 ‎【例题】（2012江苏南通，28题，14分）如图，经过点A(0，－4)的抛物线y＝x2＋bx＋c与x轴相交于点B(－2，0)和C两点，O为坐标原点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）将抛物线y＝x2＋bx＋c向上平移个单位长度、再向左平移m(m＞0)个单位长度，得到新抛物线，若新抛物线的顶点P在△ABC内，求m的取值范围；‎ ‎（3）设点M在y轴上，∠OMB＋∠OAB＝∠ACB，求AM的长． ‎ ‎【变式一】（2011福建莆田，24题，12分）已知抛物线的对称轴为直线，且与x轴交于A、B两点，与y轴交于点C，其中A(1，0)，C(0，)．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若点P在抛物线上运动（点P异于点A），当∠PCB=∠BCA时，求直线CP的解析式．‎ ‎【变式二】（1）如图，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连接AM，以AM为边作等边△AMN，连接CN． 求证：．‎ 类比探究 （2） 如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其他条件不变，（1）中结论还成立吗？请说明理由．‎ 拓展延伸 ‎（3）如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连接AM，以AM为边作等腰△AMN，使顶角． 连接CN，试探究与的数量关系，并说明理由．‎ 第22题 排除干扰建模型，认清“动”“静”用相似 ‎【例题】（2013海南省，24题，14分）如图，二次函数的图象与x轴相交于点A（－3，0）、‎ B（－1，0），与y轴相交于点C（0，3），点P是该图象上的动点；一次函数y＝kx－4k ‎（k≠0）的图象过点P交x轴于点Q．‎ ‎（1）求该二次函数的解析式；‎ ‎（2）当点P的坐标为（－4，m）时，求证：∠OPC＝∠AQC；‎ ‎（3）点M、N分别在线段AQ、CQ上，点M以每秒3个单位长度的速度从点A向点Q运动，同时，点N以每秒1个单位长度的速度从点C向点Q运动，当点M、N中有一点到达Q点时，两点同时停止运动，设运动时间为t秒．‎ ‎ ①连接AN，当△AMN的面积最大时，求t的值；‎ ‎ ②线段PQ能否垂直平分线段MN？如果能，请求出此时点P的坐标；如果不能，请说明你的理由．‎ x y O A B P M N Q C ‎【变式一】（2011河北，26题，12分）如图，在平面直角坐标系中，点P从原点O出发，沿x轴向右以每秒1个单位长的速度运动t秒（t＞0），抛物线y=x2+bx+c经过点O和点P．已知矩形ABCD的三个顶点为A（1，0），B（1，–5），D（4，0）．‎ ‎（1）求c，b（用含t的代数式表示）；‎ ‎（2）当4＜t＜5时，设抛物线分别与线段AB，CD交于点M，N．‎ ‎ ①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；‎ ‎ ②求△MPN的面积S与t的函数关系式，并求t为何值时，S＝．‎ ‎【变式二】（2011重庆潼南，26题，12分）如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，AC=BC，OA=1，OC=4，抛物线经过A，B两点，抛物线的顶点为D．‎ ‎（1）求b，c的值；‎ ‎（2）点E是直角三角形ABC斜边AB上的一动点（点A、B除外），过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E的坐标；‎ ‎（3）在（2）的条件下：‎ ‎ ①求以点E、B、F、D为顶点的四边形的面积；‎ ‎ ②在抛物线上是否存在一点P，使△EFP是以EF为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，说明理由．‎ 第23题 “一路走来”遇阻碍，“变换”拂面望眼开 ‎【例题】（2012福建福州，22，14分）如图1，已知抛物线(a≠0)经过A(3，0)、B(4，4)两点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）将直线OB向下平移m个单位长度后，得到的直线与抛物线只有一个公共点D，求m的值及点D的坐标；‎ ‎（3）如图2，若点N在抛物线上，且∠NBO=∠ABO，则在（2）的条件下，求出所有满足△POD∽△NOB的点P的坐标（点P、O、D分别与点N、O、B对应）．‎ ‎【变式一】（2011江苏镇江，24题，7分）如图，在△ABO中，已知点A（，3）、B（﹣1，﹣1）、O（0，0），正比例函数y=﹣x图象是直线l，直线AC∥x轴交直线l与点C．‎ ‎（1）C点的坐标为　 　；‎ ‎（2）以点O为旋转中心，将△ABO顺时针旋转角α（90°≤α＜180°），使得点B落在直线l上的对应点为B′，点A的对应点为A′，得到△A′OB′．‎ ‎ ①∠α=　 　；‎ ‎ ②画出△A′OB′．‎ ‎（3）写出所有满足△DOC∽△AOB的点D的坐标．‎ ‎【变式二】（2013江苏盐城，27题，12分）如图①，△ABC与△DEF都是等腰直角三角形，∠ACB=∠EDF=90°，且点D在AB边上，AB、EF的中点均为O，连结BF、CD、CO，显然点C、F、O在同一条直线上，可以证明△BOF≌△COD，则BF=CD．‎ 解决问题 （1） 将图①中的Rt△DEF绕点O旋转得到图②，猜想此时线段BF与CD的数量关系，并证明你的结论；‎ （2） 如图③，若△ABC与△DEF都是等边三角形，AB、EF的中点均为O，上述（1）中的结论仍然成立吗？如果成立，请说明理由；如不成立，请求出BF与CD之间的数量关系；‎ （3） 如图④，若△ABC与△DEF都是等腰三角形，AB、EF的中点均为O，且顶角∠ACB=∠EDF=α，请直接写出的值（用含α的式子表示出来）.‎ 第24题 “多级分类”获贯通，“相似求解”靠“双基”‎ ‎【例题】（2012云南省，23题，9分）如图，在平面直角坐标系中，直线交轴于点，交轴于点，抛物线的图象过点，并与直线相交于、 两点.‎ ‎（1）求抛物线的解析式（关系式）；‎ ‎（2）过点作交轴于点，求点的坐标；‎ ‎（3） 除点外，在坐标轴上是否存在点，使得是直角三角形？若存在，请求出点的坐标，若不存在，请说明理由.‎ ‎【变式一】（2012山东青岛，24题，12分）如图，在△ABC中，∠C＝90º，AC＝6cm，BC ‎＝8cm，D、E分别是AC、AB的中点，连接DE．点P从点D出发，沿DE方向匀速运动，‎ 速度为1cm/s；同时，点Q从点B出发，沿BA方向匀速运动，速度为2cm/s，当点P停止 运动时，点Q也停止运动．连接PQ，设运动时间为t(0＜t＜4)s．解答下列问题：‎ ‎（1）当t为何值时，PQ⊥AB？‎ ‎（2）当点Q在B、E之间运动时，设五边形PQBCD的面积为ycm2，求y与t之间的函数关系式；‎ ‎（3）在（2）的情况下，是否存在某一时刻t，使得PQ分四边形BCDE所成的两部分的面积之比为？若存在，求出此时t的值以及点E到PQ的距离h；若不存在，请说明理由．‎ ‎【变式二】（2013江苏淮安，28题，12分）如图，在△ ABC中，∠ C=90°，BC=3，AB=5．点P从点B出发，以每秒1个单位长度沿B→C→A→B的方向运动；点Q从点C出发，以每秒2个单位沿C→A→B方向的运动，到达点B后立即原速返回，若P、Q两点同时运动，相遇后同时停止，设运动时间为t秒．‎ ‎（1）当t=　 　时，点P与点Q相遇；‎ ‎（2）在点P从点B到点C的运动过程中，当t为何值时，△PCQ为等腰三角形？‎ ‎（3）在点Q从点B返回点A的运动过程中，设△PCQ的面积为S平方单位．‎ ‎①求S与t之间的函数关系式；‎ ‎②当S最大时，过点P作直线交AB于点D，将△ABC中沿直线PD折叠，使点A落在直线PC上，求折叠后的△APD与△PCQ重叠部分的面积．‎ 第25题 聚焦特殊三角形，切换视角“液体积”‎ ‎【例题】（2013河北，26题，14分）一透明的敞口正方体容器ABCD -A′B′C′D′ 装有一些 ‎ 液体，棱AB始终在水平桌面上，容器底部的倾斜角为α（∠CBE = α，如图1所示）．‎ 探究 如图1，液面刚好过棱CD，并与棱BB′ 交于 点Q，此时液体的形状为直三棱柱，其三视图及尺寸如图2所示．解决问题：‎ ‎（1）CQ与BE的位置关系是___________，BQ的长是____________dm； ‎ ‎（2）求液体的体积；（参考算法：直棱柱体积）‎ ‎（3）求α的度数．(注：，）‎ 拓展 在图1的基础上，以棱AB为轴将容器向左或向右旋转，但不能使液体溢出，图3或图4是其正面示意图．若液面与棱C′C或CB交于点P，设PC = x，BQ = y．分别就图3和图4求y与x的函数关系式，并写出相应的α的范围．‎ ‎ ‎ 延伸 在图4的基础上，于容器底部正中间位置，嵌入一平行于侧面的长方形隔板（厚度忽略不计），得到图5，隔板高NM = 1 dm，BM = CM，NM⊥BC．继续向右缓慢旋转，当α = 60°时，通过计算，判断溢出容器的液体能否达到4 dm3．‎ ‎ ‎ ‎【变式一】（2013北京，22题，5分）阅读下面材料：小明遇到这样一个问题：如图1，在边长为的正方形ABCD各边上分别截取AE=BF=CG=DH=1，当∠AFQ=∠BGM=∠CHN=∠DEP=45°时，求正方形MNPQ的面积．‎ 小明发现：分别延长QE，MF，NG，PH，交FA，GB，HC，ED的延长线于点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE是四个全等的等腰直角三角形（如图2）‎ 请回答：‎ （1） 若将上述四个等腰直角三角形拼成一个新的正方形（无缝隙，不重叠），则这个新的正方形的边长为__________；‎ ‎（2）求正方形MNPQ的面积．[中国教*育&#^‎ 参考小明思考问题的方法，解决问题：如图3，在等边△ABC各边上分别截取AD=BE=CF，再分别过点D，E，F作BC，AC，AB的垂线，得到等边△RPQ，若，则AD的长为__________．‎ ‎ ‎ ‎ ‎ ‎【变式二】（原创题）【阅读理解】（摘编自人教课标版八年级数学（下册）教材）‎ 宽与长的比是或（约为0．618）的矩形叫做黄金矩形．下面，我们用宽为4cm的矩形纸片折叠出一个黄金矩形．‎ 第一步，在矩形纸片的一端，利用图1的方法折出一个正方形，然后把纸片展平；‎ 第二步，如图2，把这个正方形折成两个相等的矩形，再把纸片展平；‎ 第三步，折出内侧矩形的对角线AB，并把它折到图4中所示的AD处；‎ 第四步，展平纸片，按照所得的D点折出DE，如图4……‎ ‎【问题解决】‎ （1） 图3中AB= cm；‎ （2） 你发现图4中有几个黄金矩形？请都写出来，并选择其中一个说明理由；‎ （3） 在图3中，连接BD，以AQ、BD为两直角边作直角三角形，求该直角三角形斜边的长.‎ 第26题 阅读“定义”重理解，两级分类显功底 ‎【例题】（2013江苏南京，27题，10分）对于两个相似三角形，如果沿周界按对应点顺序环绕的方向相同，那么称这两个三角形互为顺相似；如果沿周界按对应点顺序环绕的方向相反，那么称这两个三角形互为逆相似．‎ 例如，如图1，且沿周界ABCA与环绕的方向相同，因此△ABC 与△互为顺相似；如图2，，且沿周界ABCA与 环绕的方向相反，因此△ABC 与△互为逆相似．‎ （1） 根据图I、图II和图III满足的条件，可得下列三对相似三角形：①△ADE与△ABC； ② △GHO与△KFO； ③△NQP与△NMQ．其中，互为顺相似的是 ；互为逆相似的是 ．(填写所有符合要求的序号)‎ ‎（2）如图3，在锐角△ABC中，ÐA<ÐB<ÐC，点P在△ABC的边上(不与点A、B、C重合)．过点P画直线截△ABC，使截得的一个三角形与△ABC互为逆相似．请根据点P的不同位置，探索过点P的截线的情形，画出图形并说明截线满足的条件，不必说明理由．‎ ‎【变式一】（2013安徽，23题，14分）我们把由不平行于底边的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”，如图1，四边形ABCD即为“准等腰梯形”，其中∠B=∠C.‎ （1） 在图1所示的“准等腰梯形”ABCD中，选择合适的一个顶点引一条直线将四边形ABCD分割成一个等腰梯形和一个三角形或分割成一个等腰三角形和一个梯形（画出一种示意图即可）；‎ （2） 如图2，在“准等腰梯形”ABCD中，∠B=∠C，E为边BC上一点，若AB∥DE,AE∥DC,求证：；‎ （3） 在由不平行于BC的直线AD截△PBC所得的四边形ABCD中，∠BAD=∠ADC的平分线交于点E，若EB=EC,请问当点E在四边形ABCD内部时（即图3所示情形），四边形ABCD是不是“准等腰梯形”，为什么？若点E不在四边形ABCD内部时，情形又将如何？写出你的结论．（不必说明理由）‎ ‎【变式二】（2011江苏南京，27题，9分）如图1，P为△ABC内一点，连接PA、PB、PC，‎ 在△PAB、△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．‎ ‎（1）如图2，已知Rt△ABC中，∠ACB=90°，∠ACB＞∠A，CD是AB上的中线，过点B作BE⊥CD，垂足为E，试说明E是△ABC的自相似点．‎ ‎（2）在△ABC中，∠A＜∠B＜∠C．‎ ‎ ①如图3，利用尺规作出△ABC的自相似点P（写出作法并保留作图痕迹）；‎ ‎ ②若△ABC的内心P是该三角形的自相似点，求该三角形三个内角的度数．‎ 第27题 “理解约定”细分析，列表观察“规律现”‎ ‎【例题】（2012浙江衢州，23题，10分）课本中，把长与宽之比为的矩形纸片称为标准纸．请思考解决下列问题：‎ （1） 将一张标准纸ABCD（AB＜BC）对开，如图1所示，所得的矩形纸片ABEF是标准纸．请给予证明．‎ ‎（2）在一次综合实践课上，小明尝试着将矩形纸片ABCD（AB＜BC）进行如下操作：‎ 第一步：沿过A点的直线折叠，使B点落在AD边上点F处，折痕为AE（如图2甲）；‎ 第二步：沿过D点的直线折叠，使C点落在AD边上点N处，折痕为DG（如图2乙），此时E点恰好落在AE边上的点M处；‎ 第三步：沿直线DM折叠（如图2丙），此时点G恰好与N点重合．‎ 请你探究：矩形纸片ABCD是否是一张标准纸？请说明理由．‎ （3） 不难发现：将一张标准纸按如图3一次又一次对开后，所得的矩形纸片都是标准纸．现有一张标准纸ABCD，AB=1，BC=，问第5次对开后所得标准纸的周长是多少？探索直接写出第2012次对开后所得标准纸的周长．‎ ‎【变式一】（2012浙江宁波，25题，10分）邻边不相等的平行四边形纸片，剪去一个菱形，‎ 余下一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四 边形，称为第二次操作；……依次类推，若第n次操作余下的四边形是菱形，则称原平行四 边形为n阶准菱形，如图，平行四边形中，若，则平行四边形 为1阶准菱形．‎ ‎（1）判断与推理：‎ ‎① 邻边长分别为2和3的平行四边形是__________阶准菱形；‎ ‎② 小明为了剪去一个菱形，进行如下操作：如图，把平行四边形沿着折叠（点在上）使点落在边上的点，得到四边形，请证明四边形是菱形．‎ ‎（2）操作、探究与计算：‎ ‎① 已知平行四边形的邻边分别为1，裁剪线的示意图，并在图形下方写出的值；‎ ‎② 已知平行四边形的邻边长分别为，满足，请写出平行四边形是几阶准菱形．‎ ‎【变式二】（2011陕西省，25题，12分）如图1，在矩形ABCD中，将矩形折叠，使B落在边AD（含端点）上，落点记为E，这时折痕与边BC或边CD（含端点）交于点F，然后展开铺平，则以B、E、F为顶点的三角形△BEF称为矩形ABCD的“折痕三角形”‎ ‎（1）由“折痕三角形”的定义可知，矩形ABCD的任意一个“折痕△BEF”是一个_________三角形 ‎（2） 如图2，在矩形ABCD，AB=2，BC=4，当它的“折痕△BEF”的顶点E位于边AD的中点时，画出这个“折痕△BEF”，并求出点F的坐标；‎ ‎（3）、如图3，在矩形ABCD中， AB=2，BC=4，该矩形是否存在面积最大的“折痕△BEF”？‎ 若存在，说明理由，并求出此时点E的坐标？若不存在，为什么？‎ 第28题 “大胆猜想”靠直觉，“小心求证”依理性 ‎【例题】（2011江西，25题，10分）某数学兴趣小组开展了一次活动，过程如下：‎ 设，现把小棒依次摆放在两射线AB、AC之间，并使小棒两端分别落在两射线上．‎ ‎ 活动一：‎ 如图1所示，从点开始，依次向右摆放小棒，使小棒与小棒在端点处互相垂直，为第1根小棒．‎ ‎ 数学思考：‎ （1） 小棒能无限摆下去吗？答： （填“能”或“不能”）．‎ （2） 设．‎ ‎ ① 度；‎ ‎ ②若记小棒的长度为（为正整数，如，，．．．），求出此时、的值，并直接写出（用含的式子表示）．‎ 活动二：‎ 如图2所示，从点开始，用等长的小棒依次向右摆放，其中为第1根小棒，且=．‎ 数学思考：‎ （3） 若已经向右摆放了3根小棒，则 ， ， ．（用含的式子表示）．‎ （3） 若只能摆放4根小棒，求的范围．‎ ‎【变式一】（2012湖南岳阳，25题，8分）‎ （1） 操作发现：如图，D是等边△ABC边BA上一动点（点D与点B不重合），连接DC，以DC为边在BC上方作等边△DCF，连接AF．你能发现线段AF与BD之间的数量关系吗？并证明你发现的结论．‎ （2） 类比猜想：如图，当动点D运动至等边△ABC边BA的延长线上时，其他作法与（1）相同，猜想AF与BD在（1）中的结论是否仍然成立？‎ ‎（3）深入探究：‎ Ⅰ．如图，当动点D在等边△ABC边BA上运动时（点D与点B不重合）连接DC，以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′，连接AF、BF′，探究AF、BF′与AB有何数量关系？并证明你探究的结论．‎ Ⅱ．如图，当动点D在等边△边BA的延长线上运动时，其他作法与图③相同，Ⅰ中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论．‎ ‎【变式二】（2012江苏淮安，28题，12分）‎ 阅读理解 如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重叠部分；将余下部分沿B1A1C的平分线A1B2折叠，剪掉重叠部分；…；将余下部分沿BnAnC的平分线AnBn+1折叠，点Bn与点C重合，无论折叠多少次，只要最后一次恰好重合，我们就称∠BAC是△ABC的好角．‎ 小丽展示了确定∠BAC是△ABC的好角的两种情况。情形一：如图2，沿等腰三角形△ABC顶角∠BAC的平分线AB1折叠，点B与点C重合；情形二：如图3，沿△ABC的∠BAC的平分线AB1折叠，剪掉重叠部分；将余下的部分沿B1A1C的平分线A1B2折叠，此时点B1与点C重合．‎ 探究发现 ‎（1）△ABC中，∠B＝2∠C，经过两次折叠，∠BAC是不是△ABC的好角？ （填“是”或“不是”）．‎ ‎（2）小丽经过三次折叠发现了∠BAC是△ABC的好角，请探究∠B与∠C（不妨设∠B>∠C ‎）之间的等量关系．‎ 根据以上内容猜想：若经过n 次折叠∠BAC是△ABC的好角，则∠B与∠C不妨设∠B>∠C）之间的等量关系为 ．‎ 应用提升 ‎（3）小丽找到一个三角形，三个角分别为15°，60°，105°，发现60°和105°的两个角都是此三角形的好角．‎ 请你完成，如果一个三角形的最小角是4°，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．‎ 第29题 经典问题“再上场”，“模式识别”来破题 ‎【例题】（2012山东烟台，25，10分）‎ ‎（1）问题探究 ‎ ‎ 如图1，分别以△ABC的边AC与边BC为边，向△ABC外作正方形和正方形，过点C作直线KH交直线AB于点H，使.作，，垂足分别为点M，N．试探究线段与线段的数量关系，并加以证明．‎ ‎（2）拓展延伸 ‎ ‎ ①如图2，若将“问题探究”中的正方形改为正三角形，过点C作直线，，分别交直线AB于点，，使．作，，垂足分别为点M，N．是否仍成立？若成立，给出证明；若不成立，说明理由．  ‎ ‎ ②如图3，若将①中的“正三角形”改为“正五边形”，其他条件不变．是否仍成立？（要求：在图3中补全图形，注明字母，直接写出结论，不需证明）‎ ‎【变式一】（2011江苏盐城，27题，12分）‎ 情境观察 将矩形ABCD纸片沿对角线AC剪开，得到△ABC和△，如图1所示，将△的顶点与点A重合，并绕点A按逆时针方向旋转，使点D、A（）、B在同一条直线上，如图2所示．观察图2可知：与BC相等的线段是  ， ∠CAC′=  °．‎ 问题探究 如图3，△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外作等腰Rt△ABE和等腰Rt△ACF，过点E、F作射线GA的垂线，垂足分别为P、Q. 试探究EP与FQ之间的数量关系，并证明你的结论. ‎ 拓展延伸 如图4，△ABC中，AG⊥BC于点G，分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF，射线GA交EF于点H. 若，，试探究HE与HF之间的数量关系，并说明理由.‎ 第30题 “特例引路”含规律，“强化条件”助突破 ‎【例题】（2012吉林，26题，10分）‎ 问题情境 如图，在轴上有两点,（）.分别过点，点作轴的垂线，‎ 交抛物线于点、点.直线交直线于点，直线交直线于点,‎ 点、点的纵坐标分别记为、.‎ 特例探究 填空：‎ 当,时，=____,=______.当,时，=____,=______.[来 归纳证明 对任意,（）,猜想与的大小关系，并证明你的猜想 拓展应用 ‎（1）若将“抛物线”改为“抛物线”,其它条件不变，请直接写出与的大小关系.‎ ‎（2）连接，．当时，直接写出和的关系及四边形的形状．‎ ‎【变式】（2012江苏镇江，27题，9分）对于二次函数和一次函数，把称为这两个函数的“再生二次函数”，其中t是不为零的实数，其图象记作抛物线E．现有点A（2，0）和抛物线E上的点B（－1，n），请完成下列任务：‎ ‎【尝试】‎ ‎（1）当t=2时，抛物线的顶点坐标为 ．‎ ‎（2）判断点A是否在抛物线E上；‎ ‎（3）求n的值．‎ ‎【发现】通过（2）和（3）的演算可知，对于t取任何不为零的实数，抛物线E总过定点，坐标为 　　 ．‎ ‎【应用1】二次函数是二次函数和一次函数的一个“再生二次函数”吗？如果是，求出t的值；如果不是，说明理由；‎ ‎【应用2】以AB为边作矩形ABCD，使得其中一个顶点落在y轴上，若抛物线E经过A、B、C、D其中的一点，求出所有符合条件的t的值．‎