中考数学倒数第二题汇编含答案 110页

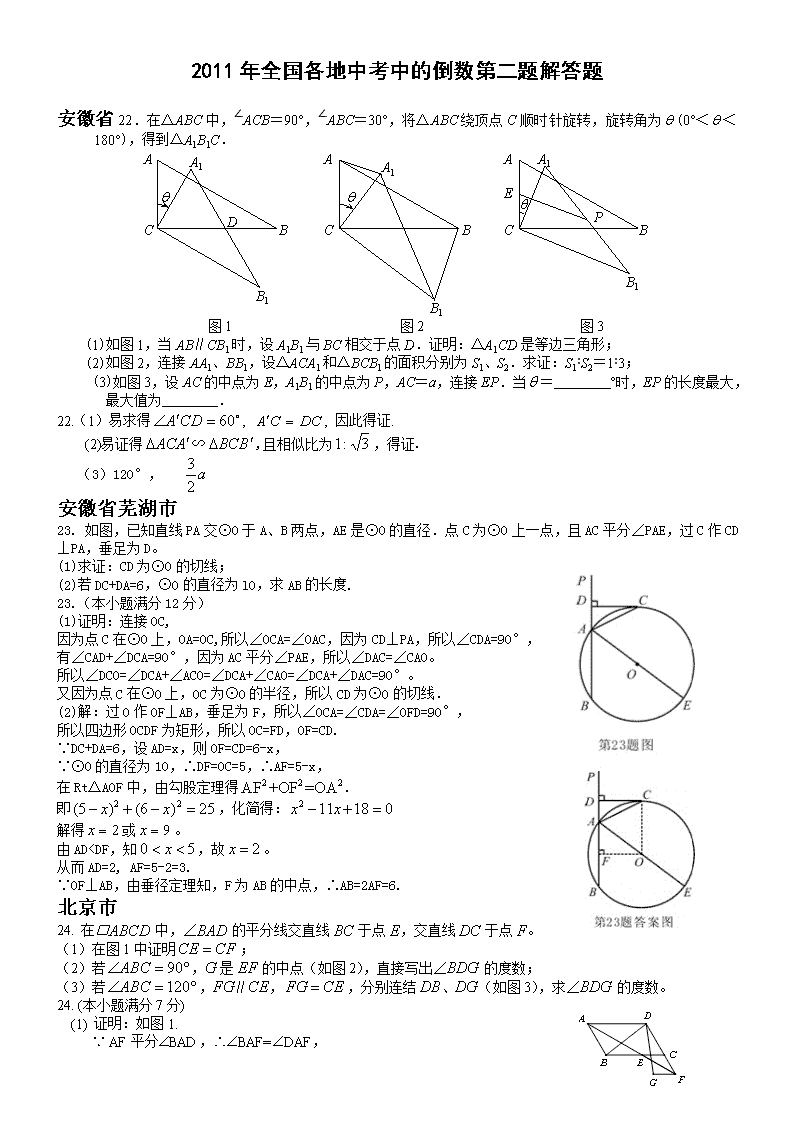
‎2011年全国各地中考中的倒数第二题解答题 安徽省22．在△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋转角为(0°＜＜180°)，得到△A1B‎1C．‎ A A1‎ A C C C A1‎ A1‎ A D B1‎ B B B B1‎ B1‎ E P 图1‎ 图2‎ 图3‎ ‎(1)如图1，当AB∥CB1时，设A1B1与BC相交于点D．证明：△A1CD是等边三角形；‎ ‎(2)如图2，连接AA1、BB1，设△ACA1和△BCB1的面积分别为S1、S2．求证：S1∶S2＝1∶3；‎ ‎ (3)如图3，设AC的中点为E，A1B1的中点为P，AC＝a，连接EP．当＝ °时，EP的长度最大，最大值为 ．‎ ‎22.（1）易求得, , 因此得证.‎ ‎(2)易证得∽,且相似比为，得证.‎ ‎（3）120°， ‎ 安徽省芜湖市 ‎23. 如图，已知直线PA交⊙0于A、B两点，AE是⊙0的直径．点C为⊙0上一点，且AC平分∠PAE，过C作CD⊥PA，垂足为D。‎ ‎(1)求证：CD为⊙0的切线；‎ ‎(2)若DC+DA=6，⊙0的直径为l0，求AB的长度.‎ ‎23.（本小题满分12分）‎ ‎(1)证明：连接OC,‎ 因为点C在⊙0上，‎0A=OC,所以∠OCA=∠OAC，因为CD⊥PA，所以∠CDA=90°，‎ 有∠CAD+∠DCA=90°，因为AC平分∠PAE，所以∠DAC=∠CAO。‎ 所以∠DC0=∠DCA+∠ACO=∠DCA+∠CAO=∠DCA+∠DAC=90°。 ‎ 又因为点C在⊙O上，OC为⊙0的半径，所以CD为⊙0的切线．‎ ‎(2)解：过0作‎0F⊥AB，垂足为F，所以∠OCA=∠CDA=∠OFD=90°，‎ 所以四边形OCDF为矩形，所以‎0C=FD，OF=CD.‎ ‎∵DC+DA=6，设AD=x，则OF=CD=6-x，‎ ‎∵⊙O的直径为10，∴DF=OC=5，∴AF=5-x，‎ 在Rt△AOF中，由勾股定理得.‎ 即，化简得：‎ 解得或。‎ 由AD0)的图象经过点C(0,1)，且与x轴交于不同的两点A、B，点A的坐标是（1，0）‎ ‎（1）求c的值；‎ ‎（2）求a的取值范围；‎ ‎（3）该二次函数的图象与直线y=1交于C、D两点，设A、B、C、D四点构成的四边形的对角线相交于点P，记△PCD的面积为S1，△PAB的面积为S2，当00, ∴y>x. ∵z-y=>0)‎ ‎∴2， （9分，没有过程直接得出酌情扣1分）‎ ‎∴ z＞y＞x. ∴⊙P的面积S的最大值为. （10分）‎ 湖南省长沙 ‎25．使得函数值为零的自变量的值称为函数的零点。例如，对于函数，令y=0，可得x=1，我们就说1是函数的零点。‎ ‎ 己知函数 (m为常数)。‎ ‎ （1）当=0时，求该函数的零点；‎ ‎（2）证明：无论取何值，该函数总有两个零点；‎ ‎（3）设函数的两个零点分别为和，且，此时函数图象与x轴的交点分别为A、B(点A在点B左侧)，点M在直线上，当MA+MB最小时，求直线AM的函数解析式。‎ ‎25. （1）当=0时，该函数的零点为和。‎ ‎（2）令y=0，得△=‎ ‎∴无论取何值，方程总有两个不相等的实数根。‎ 即无论取何值，该函数总有两个零点。‎ ‎（3）依题意有，‎ 由解得。∴函数的解析式为。‎ 令y=0，解得 ∴A()，B(4,0)‎ 作点B关于直线的对称点B’，连结AB’，‎ 则AB’与直线的交点就是满足条件的M点。‎ 易求得直线与x轴、y轴的交点分别为C（10,0），D（0,10）。‎ 连结CB’，则∠BCD=45°∴BC=CB’=6，∠B’CD=∠BCD=45°‎ ‎∴∠BCB’=90°即B’（）‎ 设直线AB’的解析式为，则 ‎，解得 ‎∴直线AB’的解析式为，‎ 即AM的解析式为。‎ 湖南省常德 ‎25、（2011•常德）已知△ABC，分别以AC和BC为直径作半圆O1，O2，P是AB的中点，‎ ‎（1）如图1，若△ABC是等腰三角形，且AC=BC，在，上分别取点E、F，使∠AO1E=∠BO‎2F，则有结论①△PO1E≌△FO2P，②四边形PO1CO2是菱形，请给出结论②的证明；‎ ‎（2）如图2，若（1）中△ABC是任意三角形，其他条件不变，则（1）中的两个结论还成立吗？若成立，请给出证明；‎ ‎（3）如图3，若PC是⊙O1的切线，求证：AB2=BC2+‎3AC2． ‎ 考点：切线的性质；全等三角形的判定；勾股定理；三角形中位线定理；菱形的判定。‎ 分析：（1）可证明△APO1与△BPO2全等，则∠AO1P=∠BO2P，再根据已知可得出EO1=FO2，PO1=PO2，则△PO1E≌△FO2P，可先证明四边形PO1CO2是平行四边形，再证明CO1=CO2，即可得出四边形PO1CO2是菱形；‎ ‎（2）由已知得出①成立，而②只是平行四边形；‎ ‎（3）直角三角形APC中，设AP=c，AC=a，PC=b，则c2=a2+b2；AB2=‎4c2=4（a2+b2），过点B作AC的垂线，交AC的延长线于D点．则CD=a，BD=2b．BC2=a2+4b2，由此得证．‎ 解答：解：（1））∵P、O1、O2分别为AB、AC、BC的中点，‎ ‎∴AP=BP，AO1=BO2，PO1BC，PO‎2AC，‎ ‎∴四边形PO1CO2是平行四边形，‎ ‎∵AC=BC，∴PO1=PO2，‎ ‎∴四边形PO1CO2是菱形；‎ ‎（2）∵P、O1、O2分别为AB、AC、BC的中点，∴AP=BP，AO1=BO2，PO1BC，PO‎2AC，‎ 即PO1=BO2，AO1=PO2，‎ ‎∴△APO1≌△BPO2；‎ ‎（3）直角三角形APC中，设AP=c，AC=a，PC=b，‎ ‎∴c2=a2+b2；AB2=‎4c2=4（a2+b2），‎ 过点B作AC的垂线，交AC的延长线于D点．‎ ‎∴CD=a，BD=2b，BC2=a2+4b2，‎ ‎∴BC2+‎3AC2=a2+4b2+‎3a2=4（a2+b2），‎ ‎∴AB2=BC2+‎3AC2．‎ 点评：本题综合考查了圆与全等的有关知识；利用中位线定理及构造三角形全等，利用全等的性质解决相关问题是解决本题的关键．‎ ‎ 湖南省衡阳 ‎26、（2011•衡阳）如图，在矩形ABCD中，AD=‎‎4cm ‎，AB=m（m＞4），点P是AB边上的任意一点（不与点A、B重合），连接PD，过点P作PQ⊥PD，交直线BC于点Q．‎ ‎（1）当m=10时，是否存在点P使得点Q与点C重合？若存在，求出此时AP的长；若不存在，说明理由；‎ ‎（2）连接AC，若PQ∥AC，求线段BQ的长（用含m的代数式表示）；‎ ‎（3）若△PQD为等腰三角形，求以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式，并写出m的取值范围．‎ 考点：相似三角形的判定与性质；等腰三角形的性质；勾股定理；矩形的性质。‎ 专题：探究型。‎ 分析：（1）假设存在一点P，使点Q与点C重合，再设AP的长为x，利用勾股定理即可用x表示出DP、PC的长，再在Rt△PCD中利用勾股定理即可求出x的值；‎ ‎（2）连接AC，设BP=x，则AP=m﹣x，由相似三角形的判定定理得出△PBQ∽△ABC，△APD∽△BQP，再根据相似三角形的对应边成比例即可求出BQ的表达式；‎ ‎（3）连接DQ，把四边形PQCD化为两个直角三角形，再用m表示出PD及CQ的长，利用三角形的面积公式即可解答．‎ 解答：解：（1）存在点P．‎ 假设存在一点P，使点Q与点C重合，如图1所示，设AP的长为x，则BP=10﹣x，‎ 在Rt△APD中，DP2=AD2+AP2，即DP2=42+x2，‎ 在Rt△PBC中，PC2=BC2+PB2，即DP2=42+（10﹣x）2，‎ 在Rt△PCD中，CD2=DP2+PC2，即102=42+x2+42+（10﹣x）2，‎ 解得x=2或8，‎ 故当m=10时，存在点P使得点Q与点C重合，此时AP=2或8；‎ ‎（2）连接AC，设BP=x，则AP=m﹣x，‎ ‎∵PQ∥AC，‎ ‎∴△PBQ∽△ABC，‎ ‎∴=，即=①，‎ ‎∵DP⊥PQ，‎ ‎∴∠APD+∠BPQ=90°，‎ ‎∵∠APD+∠ADP=90°，∠BPQ+∠PQB=90°，‎ ‎∴∠APD=∠BQP，‎ ‎∴△APD∽△BQP，‎ ‎∴=，即=②，‎ ‎①②联立得，BQ=；‎ ‎（3）连接DQ，‎ 设AP=x，由（1）知在Rt△APD中，DP2=AD2+AP2，即DP2=42+x2，‎ 在Rt△PBC中，PC2=BC2+PB2，即DP2=42+（m﹣x）2，‎ 若△PQD为等腰三角形，则42+x2=42+（m﹣x）2，‎ 解得x=，‎ ‎∵BQ=，‎ ‎∴CQ=4﹣=，‎ ‎∴S四边形DPQC=S△DPQ+S△DCQ，‎ 即S=××+××m=（m＞4）．‎ 点评：本题考查的是相似三角形的判定与性质，涉及到矩形的性质、等腰直角三角形的性质及三角形的面积公式，根据题意作出辅助线是解答此题的关键．‎ 湖南省娄底 ‎24、（2011•娄底）如图，已知二次函数y=﹣x2+mx+‎4m的图象与x轴交于A（x1，0），B（x2，0）两点（B点在A点的右边），与y轴的正半轴交于点C，且（x1+x2）﹣x1x2=10．‎ ‎（1）求此二次函数的解析式．‎ ‎（2）写出B，C两点的坐标及抛物线顶点M的坐标；‎ ‎（3）连接BM，动点P在线段BM上运动（不含端点B，M），过点P作x轴的垂线，垂足为H，设OH的长度为t，四边形PCOH的面积为S．请探究：四边形PCOH的面积S有无最大值？如果有，请求出这个最大值；如果没有，请说明理由．‎ 考点：二次函数综合题。‎ 分析：（1）由根与系数的关系，得到x1和x2的关系式进而求出m的值，所以可求此二次函数的解析式；‎ ‎（2）令y=0解一元二次方程，可求出B，C两点的坐标；把二次函数的解析式为y=﹣x2‎ ‎+2x+8配方化为顶点式可求出顶点M的坐标；‎ ‎（3）过M作MN⊥x轴于N，则ON=1，MN=9，OB=4，BN=3，再由PH∥MN，可求得PH=3BH=3（4﹣t），所以S=﹣t2+10t=﹣（t﹣）2+可求出四边形PCOH的面积S最大值．‎ 解答：解：（1）由根与系数的关系，得 ‎∵（x1+x2）﹣x1x2=10，‎ ‎∴m+‎4m=10，m=2．‎ ‎∴二次函数的解析式为y=﹣x2+2x+8．‎ ‎（2）由﹣x2+2x+8=0，解得x1=﹣2，x2=4．‎ y=﹣x2+2x+8=﹣（x﹣1）2+9．‎ ‎∴B，C，M的坐标分别为B（4，0），C（0，8），M（1，9）．‎ ‎（3）如图，过M作MN⊥x轴于N，则ON=1，MN=9，OB=4，BN=3．‎ ‎∵OH=t（1＜t＜4），∴BH=4﹣t．‎ 由PH∥MN，可求得PH=3BH=3（4﹣t），‎ ‎∴S=（PH+CO）•OH ‎=（12﹣3t+8）t ‎=﹣t2+10t（1＜t＜4）．‎ S=﹣t2+10t=﹣（t﹣）2+．‎ ‎∵1＜＜4．‎ ‎∴当t=时，S有最大值，其最大值为．‎ 点评：本题考查了二次函数的综合应用，将函数知识与方程、几何知识有机地结合在一起．这类试题一般难度较大．解这类问题关键是善于将函数问题转化为方程问题，善于利用几何图形的有关性质、定理和二次函数的知识，并注意挖掘题目中的一些隐含条件．‎ 性质求解．‎ 湖南省邵阳 ‎23．数学课堂上，徐老师出示一道试题：‎ ‎ 如图（十）所示，在正三角形ABC中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠ACP的平分线上一点．若∠AMN＝60°，求证：AM＝MN．‎ ‎(1)经过思考，小明展示了一种正确的证明过程．请你将证明过程补充完整．‎ ‎ 证明：在AB上截取EA＝MC，连结EM，得△AEM．‎ ‎ ∵∠1＝180°－∠AMB－∠AMN，∠2＝180°－∠AMB－∠B，∠AMN＝∠B＝60°，∴∠1＝∠2．‎ ‎ 又CN平分∠ACP，∠4＝∠ACP＝60°．∴∠MCN＝∠3＋∠4＝120°…………①‎ 又∵BA＝BC，EA＝MC，∴BA－EA＝BC－MC，即BE＝BM．‎ ‎∴△BEM为等边三角形．∴∠6＝60°．∴∠5＝180°－∠6＝120°．………②‎ ‎∴由①②得∠MCN＝∠5．‎ 在△AEM和△MCN中，∵∠1＝∠2． AE=MC ， ∠MCN＝∠5．‎ ‎∴△AEM≌△MCN (ASA)．∴AM＝MN．‎ ‎(2)若将试题中的“正三角形ABC”改为“正方形A1B‎1C1D‎1”‎（如图），N1是∠D‎1C1P1的平分线上一点，则当∠A‎1M1N1＝90°时，结论A‎1M1＝M1N1．是否还成立？（直接写出答案，不需要证明）‎ ‎【答案】：成立 在上截取 ‎(3) 若将题中的“正三角形ABC”改为“正多边形AnBnCnDn…Xn”，请你猜想：当∠AnMnNn＝ °时，结论AnMn＝MnNn仍然成立？（直接写出答案，不需要证明）‎ 图10‎ ‎ ‎图11‎ ‎【解题思路】：∠AMN=60°＝ （3－2）/3 ×180°∠A‎1M1N1=90°＝（4－2）/4 ×180°‎ ‎∠AnMnNn= （n－2）/n ×180° 【点评】：本题考察了三角形全等的判定，当全等三角形不明确时构建全等三角形是本题的主旨，如何构建就是个人长期学习练习形成的，难度较大的是第三问，这里如果能快速判定该角度数是180的若干倍，且这个倍数与正多边形的边数有内在联系将容易分析。难度较大 湖南省湘潭 ‎25、（2011•湘潭）如图，直线y=3x+3交x轴于A点，交y轴于B点，过A、B两点的抛物线交x轴于另一点C（3，0）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在抛物线的对称轴上是否存在点Q，使△ABQ是等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．‎ 考点：二次函数综合题。‎ 分析：（1）由直线y=3x+3交x轴于A点，交y轴于B点，即可求得点A与B的坐标，又由过A、B两点的抛物线交x轴于另一点C（3，0），利用两点式法即可求得抛物线的解析式；‎ ‎（2）分别从AB=BQ，AQ=BQ，AB=AQ三方面去分析，注意抓住线段的求解方法，借助于方程求解即可求得答案．‎ 解答：解：（1）∵当x=0时，y=3，‎ 当y=0时，x=﹣1，‎ ‎∴A（﹣1，0），B（0，3），‎ ‎∵C（3，0），‎ 设抛物线的解析式为y=a（x+1）（x﹣3），‎ ‎∴3=a×1×（﹣3），‎ ‎∴a=﹣1，‎ ‎∴此抛物线的解析式为y=﹣（x+1）（x﹣3）=﹣x2+2x+3；‎ ‎（2）存在．‎ ‎①∵抛物线的对称轴为：x==1，‎ ‎∴如图对称轴与x轴的交点即为Q1，‎ ‎∵OA=OQ1，BO⊥AQ1，‎ ‎∴“当Q1B=AB时，设Q（1，q），‎ ‎∴1+（q﹣3）2=10，‎ ‎∴q=0，或q=6，‎ ‎∴Q（1，0）或Q（1，6）．‎ 当Q‎2A=Q2B时，设Q2的坐标为（1，m），‎ ‎∴22+m2=12+（3﹣m）2，‎ ‎∴m=1，‎ ‎∴Q2（1，1）；‎ 当Q‎3A=AB时，设Q3（1，n），‎ ‎∴22+n2=12+32，‎ ‎∴n=±，‎ ‎∴Q3（1，），Q4（1，﹣）．‎ ‎∴符合条件的Q点坐标为Q1（1，0），Q2（1，1），Q3（1，），Q4（1，﹣），Q5（1，6）．．‎ 点评：此题考查了待定系数法求二次函数的解析式与等腰三角形的性质等知识．此题难度适中，注意分类讨论思想，方程思想与数形结合思想的应用是解此题的关键，还要注意别漏解．‎ 湖南省益阳 ‎20．如图9，已知抛物线经过定点A（1，0），它的顶点P是y轴正半轴上的一个动点，P点关于x轴的对称点为P′，过P′ 作x轴的平行线交抛物线于B、D两点（B点在y轴右侧），直线BA交y轴于C点．按从特殊到一般的规律探究线段CA与CB的比值：‎ ‎（1）当P点坐标为（0，1）时，写出抛物线的解析式并求线段CA与CB的比值；‎ ‎（2）若P点坐标为（0，m）时（m为任意正实数），线段CA与CB的比值是否与⑴所求的比值相同？请说明理由． ‎ 图9‎ x y B A P′‎ P ‎1‎ O C D ‎.‎ ‎.‎ ‎.‎ ‎.‎ ‎.‎ ‎.‎ ‎20．解：⑴ 设抛物线的解析式为 ， ……………………1分 ‎　 抛物线经过 ， ， ‎ ‎　 .　 ……………………………………2分 ‎,‎ ‎ ∥,,‎ 由，‎ ‎,. …………………………………………3分 ‎ ‎，∽， …………………………………4分 ‎． 　　 　 …………………………………5分 ‎⑵ 设抛物线的解析式为　　 　……………………6分 ‎，‎ ‎．　　　　　 ………………………………………………7分 ‎∥， ‎ ‎，，，，‎ ‎，，　　 　………………………………………8分 同⑴得 　　　　　 　………………………………9分 ‎．　　　 　 …………………………10分 湖南省永州 ‎24、（2011•永州）如图，已知二次函数y=﹣x2+bx+c的图象经过A（﹣2，﹣1），B（0，7）两点．‎ ‎（1）求该抛物线的解析式及对称轴；‎ ‎（2）当x为何值时，y＞0？‎ ‎（3）在x轴上方作平行于x轴的直线l，与抛物线交于C，D两点（点C在对称轴的左侧），过点C，D作x轴的垂线，垂足分别为F，E．当矩形CDEF为正方形时，求C点的坐标．‎ 考点：二次函数综合题。‎ 分析：（1）根据待定系数法求二次函数解析式，再用配方法或公式法求出对称轴即可；‎ ‎（2）求出二次函数与x轴交点坐标即可，再利用函数图象得出x取值范围；‎ ‎（3）利用正方形的性质得出横纵坐标之间的关系即可得出答案．‎ 解答：解：（1）∵二次函数y=﹣x2+bx+c的图象经过A（﹣2，﹣1），B（0，7）两点．‎ ‎∴，解得：，‎ ‎∴y=﹣x2+2x+7，=﹣（x2﹣2x）+7，=﹣[（x2﹣2x+1）﹣1]+7，=﹣（x﹣1）2+8，‎ ‎∴对称轴为：x=1．‎ ‎（2）当y=0，‎ ‎0=﹣（x﹣1）2+8，∴x﹣1=±2，x1=1+2，x2=1﹣2，∴抛物线与x轴交点坐标为：（1﹣2，0），（1+2，0），‎ ‎∴当1﹣2＜x＜1+2时，y＞0；‎ ‎（3）当矩形CDEF为正方形时，‎ 假设C点坐标为（x，﹣x2+2x+7），‎ ‎∴D点坐标为（﹣x2+2x+7+x，﹣x2+2x+7），‎ 即：（﹣x2+3x+7，﹣x2+2x+7），‎ ‎∵对称轴为：x=1．‎ ‎∴﹣x2+3x+7﹣1=﹣x+1，‎ 解得：x1=﹣1，x2=5，‎ x=﹣1时，﹣x2+2x+7=4．‎ ‎∴C点坐标为：（﹣1，4）．‎ 点评：此题主要考查了待定系数法求二次函数解析式以及利用图象观察函数值和正方形性质等知识，根据题意得出C、D两点坐标之间的关系是解决问题的关键．‎ 湖南省岳阳 ‎25(本题满分8分)如图（1），将菱形纸片AB（E）CD（F）沿对角线BD（EF）剪开得到△ABD和△ECF，固定△ABD，并把△ABD与△ECF叠放在一起。‎ （1） 操作：如图（1），将△ECF的顶点F固定在△ABD的BD边上的中点处，△ECF绕点F在BD边上方左右旋转，设旋转时FC交BA于点H（H点不与B点重合）。FE交DA于点G（G点不与D点重合）。‎ 求证：BH·GD=BF2‎ 证明：根据图②操作有∠B=∠D=∠CFE, BF=DF 在△DFG中，∠D+∠DFG+DGF=180°，而∠DFG+∠CFE+BFH=180°‎ ‎∴ ∠BFH=∠DGF, 又∠B=∠D ‎∴△BFH∽△DGF ∴= 由于BF=DF ∴BF2=BH·DG ‎（2）操作：如图，△ECF的顶点F在△ABD的BD边上滑动（F点不与B、D点重合），且CF始终经过A，过点A作AG∥CE，交FE于点G，连接DG。探究：FD+DG=____________。请予证明。‎ 解：探究得出：FD+DG=BD 证明：∵AG∥CE, ∴∠FAG=∠C,∠FGA=∠E ‎∵∠CFE=∠E, ∴∠E=∠FGA ∴AG=AF ‎ 根据菱形有：∠BAD=∠FCE ∴∠BAD=∠FAG, 即：∠BAF+∠FAD=∠FAD+∠DAG ‎∴∠BAF=∠DAG 在△ABF与△ADG中, ∴△ABF≌△ADG ∴BF=DG ‎∴DF+DG=DF+BF=BD ‎ ‎ 湖南省株洲 ‎23．如图，矩形中，点是线段上一动点，为的中点， 的延长线交于.‎ ‎（1）求证：；‎ ‎（2）若厘米，厘米，从点出发，以‎1厘米/秒的速度向运动（不与重合）.设点运动时间为秒，请用表示的长；并求为何值时，四边形是菱形．‎ ‎23．（1）证明：四边形是矩形，‎ ‎∥ …… 1分 ‎，又，‎ ‎△≌△ …… 3分 ‎ …… 4分 ‎（2）解法一： …… 5分 四边形是矩形，，‎ ‎，，，. ‎ 当四边形是菱形时， ⊥，，又 ‎△∽△， …… 6分 ‎，即， …… 7分 解得,即运动时间为秒时，四边形是菱形. …… 8分 解法二： …… 5分 当四边形是菱形时， …… 6分 四边形是矩形，，在△中，‎ ‎， ， …… 7分 ‎ 解得,即运动时间为秒时，四边形是菱形. …… 8分 吉林省 ‎27.如图，抛物线1 :y=-x2平移得到抛物线，且经过点O(0.0)和点A(4.0)，的顶点为点B，它的对称轴与相交于点C,设、与BC围成的阴影部分面积为S,解答下列问题：‎ ‎（1）求表示的函数解析式及它的对称轴，顶点的坐标。‎ ‎（2）求点C的坐标，并直接写出S的值。‎ ‎（3）在直线AC上是否存在点P，使得S△POA＝S？若存在，求点P的坐标；若不存在，请说明理由。‎ ‎27. 解：（1）设l2的函数解析式为y＝－x2＋bx＋c 把（4.0）代入函数解析式，得 ‎ 解得 ‎∴y＝－x2＋4x ‎∵y＝－x2＋4x＝－（x－2）2＋4‎ ‎∴l2的对称轴是直线x＝2，顶点坐标B（2，4）‎ ‎（2）当x＝2时，y＝－x2＝－4‎ ‎∴C点坐标是（2，－4）‎ S＝8‎ ‎（3）存在 设直线AC表示的函数解析式为y＝kx＋n 把A（4，0），C（2，－4）代入得 解得 ‎∴y＝2x－8‎ 设△POA的高为h S△POA＝OA·h=2h=4‎ 设点P的坐标为（m,‎2m-8). ∵S△POA＝S 且S＝8‎ ‎∴S△POA＝×8=4‎ 当点P在轴上方时，得× 4（‎2m-8)=4,‎ 解得m=5,‎ ‎∴‎2m-8=2.‎ ‎∴P的坐标为（5.2）.‎ 当点P在轴下方时，得× 4（8‎-2m)=4.‎ 解得m=3,‎ ‎∴‎2m-8=-2‎ ‎∴点P的坐标为（3，-2）.‎ 综上所述，点P的坐标为（5，-2）或（3，-2）。‎ 吉林省长春 ‎25．甲、乙两组工人同时加工某种零件，乙组工作中有一次停产更换设备，更换设备后，乙组的工作效率是原来的2倍．两组各自加工零件的数量(件)与时间(时)的函数图象如图所示．‎ ‎（1）求甲组加工零件的数量y与时间之间的函数关系式．（2分）‎ ‎（2）求乙组加工零件总量的值．（3分）‎ ‎（3）甲、乙两组加工出的零件合在一起装箱，每够300件装一箱，零件装箱的时间忽略不计，求经过多长时间恰好装满第1箱？再经过多长时间恰好装满第2箱？（5分）‎ ‎25．解：（1）设甲组加工的零件数量y与时间x的函数关系式为．‎ 根据题意，得，解得． ‎ 所以，甲组加工的零件数量y与时间x的函数 关系式为. （2分）‎ ‎（2）当时，．‎ ‎ 因为更换设备后，乙组工作效率是原来的2倍，‎ ‎ 所以，．解得． （5分）‎ ‎（3）乙组更换设备后，乙组加工的零件的个数y与时间x的函数关系式为 ‎．‎ 当0≤x≤2时，．解得．舍去．‎ 当20,点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位.‎ ‎(1)写出A点的坐标和AB的长;‎ ‎(2)当点P、Q运动了t秒时,以点Q为圆心,PQ为半径的⊙Q与直线、y轴都相切,求此时a的值.‎ ‎ 答案:(1)A(-4,0),AB=5.‎ ‎(2)由题意得：AP=4t,AQ=5t,,又∠PAQ=∠QAB,∴△APQ∽△AOB.∴∠APQ=∠AOB=90°。‎ ‎∵点P在上，∴⊙Q在运动过程中保持与相切。‎ ‎①当⊙Q在y轴右侧与y轴相切时，设与⊙Q相切于F，由△APQ∽△AOB得 ,∴PQ=6,‎ 连接QF，则QF=PQ, △QFC∽△APQ∽△AOB得.‎ ‎∴,,∴QC=,a=OQ+QC=.‎ ‎②当⊙Q在y轴左侧与y轴相切时，设与⊙Q相切于E, 由△APQ∽△AOB得,∴PQ=.‎ 连接QE，则QE=PQ,由△QEC∽△APQ∽△AOB得，∴，，‎ ‎∴QC=,a=QC-OQ=.∴a的值为和。‎ 江西省 ‎ ‎24.将抛物线c1：y=沿x轴翻折，得抛物线c2，如图所示.‎ ‎（1）请直接写出抛物线c2的表达式.‎ ‎（2）现将抛物线c1向左平移m个单位长度，平移后得到的新抛物线的顶点为M，与x轴的交点从左到右依次为A，B；将抛物线c2向右也平移m个单位长度，平移后得到的新抛物线的顶点为N，与x轴交点从左到右依次为D，E.‎ ‎①当B，D是线段AE的三等分点时，求m的值；‎ ‎②在平移过程中，是否存在以点A，N，E，M为顶点的四边形是矩形的情形？若存在，请求出此时m的值；若不存在，请说明理由.‎ y x O c1‎ c2‎ 六、24．解：（1）. ………………2分 ‎（2）①令，得：，‎ ‎ 则抛物线c1与轴的两个交点坐标为（-1,0），（1,0）.‎ ‎∴A（-1-m，0），B（1-m，0）.同理可得：D（-1+m，0），E（1+m，0）.‎ 当时，如图①，，∴. ……4分 当时，如图②，， ∴. …………6分 y x O A D B E M N 图①‎ y x O A D B E M N 图②‎ ‎∴当或2时，B，D是线段AE的三等分点. ‎ ‎②存在. ………………7分 方法一 理由：连接AN、NE、EM、MA.依题意可得：.‎ 即M，N关于原点O对称， ∴. ‎ ‎∵， ∴A，E关于原点O对称， ∴，‎ ‎∴四边形ANEM为平行四边形. ………………8分 要使平行四边形ANEM为矩形，必需满足,‎ 即， ∴.‎ ‎∴当时，以点A，N，E，M为顶点的四边形是矩形. …………10分 方法二 理由：连接AN、NE、EM、MA. 依题意可得：.‎ 即M，N关于原点O对称， ∴. ‎ ‎∵， ∴A，E关于原点O对称， ∴，‎ ‎∴四边形ANEM为平行四边形. ………………8分 ‎∵，‎ ‎，‎ ‎，‎ 若，则，∴.‎ 此时△AME是直角三角形，且∠AME=90°.‎ ‎∴当时，以点A，N，E，M为顶点的四边形是矩形. …………10分 江西省 ‎24.已知：抛物线 的顶点为A，与x轴的交点为B，C（点B在点C的左侧）.‎ ‎(1)直接写出抛物线对称轴方程；‎ ‎（2）若抛物线经过原点，且△ABC为直角三角形，求a，b的值；‎ ‎（3）若D为抛物线对称轴上一点，则以A，B，C，D为顶点的四边形能否为正方形？若能，请写出a，b满足的关系式；若不能，说明理由.‎ ‎24．解：（1）抛物线对称轴方程：. ………2分 ‎（2）设直线与轴交于点E,则E（2,0）.‎ ‎∵抛物线经过原点， ∴B(0,0),C(4,0). ………3分 ‎∵△ABC为直角三角形，根据抛物线的对称性可知,‎ ‎∴,‎ ‎∴A(2,-2)或(2,2).‎ 当抛物线的顶点为A(2,-2)时，，把(0,0)代入，得：，此时，. ………5分 当抛物线的顶点为A(2,2)时，，把(0,0)代入，得：，此时，.‎ O x y A B C E ‎∴，或，. ………7分 ‎（3）依题意，B、C关于点E中心对称，当A,D也关 于点E对称，且时， 四边形ABDC是正方形.‎ ‎ ∵， ∴， ∴，‎ ‎ 把代入，得 ，‎ ‎ ∵， ∴. ………10分 江西省南昌 ‎ ‎25.如图所示，抛物线m：y=ax2+b（a＜0，b＞0）与x轴于点A、B（点A在点B的左侧），与y轴交于点C.将抛物线m绕点B旋转180°，得到新的抛物线n，它的顶点为C1，与x轴的另一个交点为A1.‎ ‎(1)当a=－1,b=1时，求抛物线n的解析式；‎ ‎(2)四边形AC‎1A1C是什么特殊四边形，请写出结果并说明理由；‎ ‎(3)若四边形AC‎1A1C为矩形，请求出a,b应满足的关系式.‎ C B A C1‎ A1‎ x y O 七、25．解：（1）当时，抛物线的解析式为：.‎ ‎ 令，得：. ∴C（0,1）.‎ ‎ 令，得：. ∴A（-1,0），B（1,0）‎ ‎ ∵C与C1关于点B中心对称，‎ ‎ ∴抛物线的解析式为： ………4分 ‎（2）四边形AC‎1A1C是平行四边形. ………5分 ‎ 理由：∵C与C1、A与A1都关于点B中心对称，‎ ‎ ∴,‎ ‎ ∴四边形AC‎1A1C是平行四边形. ………8分 ‎（3）令，得：. ∴C（0,）.‎ ‎ 令，得：, ∴,‎ ‎ ∴, ………9分 ‎ ∴.‎ ‎ 要使平行四边形AC‎1A1C是矩形，必须满足,‎ ‎ ∴， ∴，‎ ‎ ∴. ∴应满足关系式. ………10分 辽宁省本溪 ‎25、在四边形ABCD中，对角线AC、BD相交于点O，设锐角∠DOC=α，将△DOC按逆时针方向旋转得到△D′OC′（0°＜旋转角＜90°）连接AC′、BD′，AC′与BD′相交于点M．‎ ‎（1）当四边形ABCD是矩形时，如图1，请猜想AC′与BD′的数量关系以及∠AMB与α的大小关系，并证明你的猜想；‎ ‎（2）当四边形ABCD是平行四边形时，如图2，已知AC=BD，请猜想此时AC′与BD′的数量关系以及∠AMB与α的大小关系，并证明你的猜想；‎ ‎（3）当四边形ABCD是等腰梯形时，如图3，AD∥BC，此时（1）AC′与BD′的数量关系是否成立？∠AMB与α的大小关系是否成立？不必证明，直接写出结论．‎ ‎ ‎ ‎25. 解：（1）AC′=BD′，∠AMB=α，‎ 证明：在矩形ABCD中，AC=BD，OA=OC=AC，OB=OD=BD，‎ ‎∴OA=OC=OB=OD，‎ 又∵OD=OD′，OC=OC′，‎ ‎∴OB=OD′=OA=OC′，‎ ‎∵∠D′OD=∠C′OC，‎ ‎∴180°-∠D′OD=180°-∠C′OC，‎ ‎∴∠BOD′=∠AOC′，‎ ‎∴△BOD′≌△AOC′，‎ ‎∴BD′=AC′，‎ ‎∴∠OBD′=∠OAC′，‎ 设BD′与OA相交于点N，‎ ‎∴∠BNO=∠ANM，‎ ‎∴180°-∠OAC′-∠ANM=180°-∠OBD′-∠BNO，‎ 即∠AMB=∠AOB=∠COD=α，‎ 综上所述，BD′=AC′，∠AMB=α，‎ ‎（2）AC′=kBD′，∠AMB=α，‎ 证明：在平行四边形ABCD中，OB=OD，OA=OC，‎ 又∵OD=OD′，OC=OC′，‎ ‎∴OB：OA=OD′：C′，‎ ‎∵∠D′OD=∠C′OC，‎ ‎∴180°-∠D′OD=180°-∠C′OC，‎ ‎∴∠BOD′=∠AOC′，‎ ‎∴△BOD′∽△AOC′，‎ ‎∴BD′：AC′=OB：OA=BD：AC，‎ ‎∵AC=kBD，‎ ‎∴AC′=kBD′，‎ ‎∵△BOD′∽△AOC′，‎ 设BD′与OA相交于点N，‎ ‎∴∠BNO=∠ANM，‎ ‎∴180°-∠OAC′-∠ANM=180°-∠OBD′-∠BNO，即∠AMB=∠AOB=α，‎ 综上所述，AC′=kBD′，∠AMB=α，‎ ‎（3）AC′=BD′成立，∠AMB=α不成立．‎ 辽宁省大连 ‎25、（2011•大连）在△ABC中，∠A=90°，点D在线段BC上，∠EDB=∠C，BE⊥DE，垂足为E，DE与AB相交于点F．‎ ‎（1）当AB=AC时，（如图1），‎ ‎①∠EBF=　22.5　°；‎ ‎②探究线段BE与FD的数量关系，并加以证明；‎ ‎（2）当AB=kAC时（如图2），求的值（用含k的式子表示）．‎ 考点：相似三角形的判定与性质；角平分线的性质；等腰直角三角形。‎ 专题：常规题型；计算题。‎ 分析：（1）①根据题意可判断△ABC为等腰直角三角形，据此即可推断∠C=45°，进而可知∠EDB=22.5°．然后求出∠EBF的度数．‎ ‎②根据题意证明△BEF∽△DEB，然后利用相似三角形的性质，得到BE与FD的数量关系．‎ ‎（2）作∠ACB的平分线，得到∠C的正切值，然后证明△BEF∽△DEB，利用三角形相似的性质得到BE与FD的数量关系．‎ 解答：解：（1）①∵AB=AC∠A=90°‎ ‎∴∠ABC=∠C=45°‎ ‎∵∠EDB=∠C ‎∴∠EDB=22.5°‎ ‎∵BE⊥DE ‎∴∠EBD=67.5°‎ ‎∴∠EBF=67.5°﹣45°=22.5°‎ ‎②在△BEF和△DEB中 ‎∵∠E=∠E=90°‎ ‎∠EBF=∠EDB=22.5°‎ ‎∴△BEF∽△DEB 如图：‎ BG平分∠ABC，‎ ‎∴BG=GD△BEG是等腰直角三角形 设EF=x，BE=y，‎ 则：BG=GD=y FD=y+y﹣x ‎∵△BEF∽△DEB ‎∴= 即：= 得：x=（﹣1）y ‎∴FD=y+y﹣（﹣1）y=2y ‎∴FD=2BE．‎ ‎（2）如图：‎ 作∠ACB的平分线CG，交AB于点G，‎ ‎∵AB=kAC ‎∴设AC=b，AB=kb，BC=b 利用角平分线的性质有：‎ = 即：= 得：AG= ‎∵∠EDB=∠ACB ‎∴tan∠EDB=tan∠ACG= ‎∵∠EDB=∠ACB ‎∠ABC=90°﹣∠ACB ‎∴∠EBF=90°﹣∠ABC﹣∠EDB=∠ACB ‎∴△BEF∽△DEB ‎∴EF=BE ED=BE=EF+FD ‎∴FD=BE﹣BE=BE．‎ ‎∴=．‎ 点评：本题考查的是相似三角形的判定与性质，（1）利用等腰直角三角形的性质进行判定和计算．（2）结合图形利用三角函数和相似三角形进行计算求出线段间的关系．‎ 辽宁省丹东 ‎25、（2011•丹东）己知：正方形ABCD．‎ ‎（1）如图1，点E、点F分别在边AB和AD上，且AE=AF．此时，线段BE、DF的数量关系和位置关系分别是什么？请直接写出结论．‎ ‎（2）如图2，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当0°＜α＜90°时，连接BE、DF，此时（1）中的结论是否成立，如果成立，请证明；如果不成立，请说明理由．‎ ‎（3）如图3，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当a=90°时，连接BE、DF，猜想沟AE与AD满足什么数量关系时，直线DF垂直平分BE．请直接写出结论．‎ ‎（4）如图4，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当90°＜α＜180°时，连接BD、DE、EF、FB得到四边形BDEF，则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形？请直接写出结论．‎ 考点：旋转的性质；全等三角形的判定与性质；线段垂直平分线的性质；正方形的性质。‎ 专题：证明题。‎ 分析：（1）根据正方形的性质，AB=AD，由AE=AF，可得BE=DF且BE⊥DF；‎ ‎（2）通过证明△DFA≌△BEA，可得（1）中的结论依然成立；‎ ‎（3）连接BD，直线DF垂直平分BE，可得AD+AE=BD，BD=AD，解答出即可；‎ ‎（4）如图，通过证明△DAF≌△BAE，可得DF=BE，结合（2）中结论，可得到各边中点所组成的四边形的形状；‎ 解答：证明：（1）BE=DF且BE⊥DF；‎ ‎（2）在△DFA和△BEA中，‎ ‎∵∠DAF=90°﹣∠FAB，∠BAE=90°﹣∠FAB，‎ ‎∴∠DAF=∠BAE，‎ 又AB=AD，AE=AF，‎ ‎∴△DFA≌△BEA，‎ ‎∴BE=DF；∠ADF=∠ABE，‎ ‎∴BE⊥DF；‎ ‎（3）AE=（﹣1）AD；‎ ‎（4）正方形．‎ 点评：本题考查了旋转的性质、全等三角形的判定和性质、线段的垂直平分线及正方形的性质，本题的综合性较强，掌握并熟练应用以上性质是解答本题的关键．‎ 辽宁省抚顺 ‎25. 如图1，在△ABC中，∠ABC＝90°，AB＝BC，BD为斜边AC上的中线，将△ABD绕点D顺时针旋转α(0°＜α＜180°)，得到△EFD，点A的对应点为点E，点B的对应点为点F，连接BE、CF.‎ ‎(1)判断BE与CF的位置、数量关系，并说明理由；‎ ‎(2)若连接BF、CE，请直接写出在旋转过程中四边形BEFC能形成哪些特殊四边形；‎ ‎(3)如图2，将△ABC中AB＝BC改成AB≠BC时，其他条件不变，直接写出α为多少度时(1)中的两个结论同时成立．‎ ‎25. (1)FC＝BE，FC⊥BE.‎ 证明：∵　∠ABC＝90°，BD为斜边AC的中线，AB＝BC，‎ ‎∴　BD＝AD＝CD.‎ ‎∠ADB＝∠BDC＝90°.‎ ‎∵　△ABD旋转得到△EFD，‎ ‎∴　∠EDB＝∠FDC.‎ ED＝BD，FD＝CD.‎ ‎∴　△BED≌△CFD.‎ ‎∴　BE＝CF.(5分)‎ ‎∴　∠DEB＝∠DFC.‎ ‎∵　∠DNE＝∠FNB，‎ ‎∴　∠DEB＋∠DNE＝∠DFC＋∠FNB.‎ ‎∴　∠FMN＝∠NDE＝90°.‎ ‎∴　FC⊥BE.‎ ‎(2)等腰梯形和正方形.‎ ‎(3)当α＝90°(1)两个结论同时成立.‎ 辽宁省阜新 ‎24．（11·辽阜新）如图，点P是正方形ABCD对角线AC上一动点，点E在射线BC上，且PE＝EB，连接PD，O为AC中点．‎ ‎（1）如图1，当点P在线段AO上时，试猜想PE与PD的数量关系和位置关系，不用说明理由；‎ ‎（2）如图2，当点P在线段OC上时，（1）中的猜想还成立吗？请说明理由；‎ ‎（3）如图3，当点P在AC的延长线上时，请你在图3中画出相应的图形（尺规作图，保留作图痕迹，不写作法），并判断（1）中的猜想是否成立？若成立，请直接写出结论；若不成立，请说明理由．‎ A B C D P E O ‎·‎ A B C D P E O ‎·‎ A B C D O ‎·‎ ‎【答案】（1）PE＝PD且PE⊥PD………………2分 A B C D P E O ‎·‎ ‎1‎ ‎2‎ ‎5‎ ‎4‎ ‎3‎ ‎（2）成立………………3分 理由：∵四边形ABCD是正方形 ‎∴BC＝DC，∠BCP＝∠DCP＝45°，∠BCD＝90°‎ 又∵PC＝PC ‎∴△BCP≌△DCP ‎∴PB＝PD，∠1＝∠2‎ 又∵PE＝PB ‎∴PE＝PD，∠1＝∠3………………5分 A B C D O ‎·‎ P E ‎∴∠2＝∠3[‎ ‎∵∠BCD＝90°‎ ‎∴∠DCE＝90°‎ ‎∴∠DPE＝180°―∠2―∠5‎ ‎∠DCE＝180°―∠3―∠4‎ 又∵∠4＝∠5‎ ‎∴∠DPE＝∠DCE＝90°‎ 即PE⊥PD………………9分 ‎（3）仍然成立………………10分 作图如图………………12分 辽宁省沈阳市 ‎24．已知，△ABC为等边三角形，点D为直线BC上一动点（点D不与B、C重合）．以AD为边作菱形ADEF，使∠DAF=60°，连接CF．‎ ‎⑴如图1，当点D在边BC上时，‎ 求证：∠ADB=∠AFC；②请直接判断结论∠AFC=∠ACB＋∠DAC是否成立；‎ ‎⑵如图2，当点D在边BC的延长线上时，其他条件不变，结论∠AFC=∠ACB＋∠DAC是否成立？请写出∠AFC、∠ACB、∠DAC之间存在的数量关系，并写出证明过程；‎ ‎⑶如图3，当点D在边CB的延长线上时，且点A、F分别在直线BC的异侧，其他条件不变，请补全图形，并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系．‎ A A A B B B C C C D D D E F F E 第24题图 图1‎ 图2‎ 图31‎ ‎24．⑴①证明：∵△ABC为等边三角形，‎ ‎∴AB=AC，∠BAC=60°‎ ‎∵∠DAF=60°‎ ‎∴∠BAC=∠DAF ‎∴∠BAD=∠CAF ‎∵四边形ADEF是菱形，∴AD=AF A B C D F ‎∴△ABD≌△ACF ‎∴∠ADB=∠AFC ‎②结论：∠AFC=∠ACB＋∠DAC成立．‎ ‎⑵结论∠AFC=∠ACB＋∠DAC不成立．‎ ‎∠AFC、，∠ACB、∠DAC之间的等量关系是 ‎∠AFC=∠ACB－∠DAC（或这个等式的正确变式）‎ 证明：∵△ABC为等边三角形 A B C D F E ‎∴AB=AC ‎∠BAC=60°‎ ‎∵∠BAC=∠DAF ‎∴∠BAD=∠CAF ‎∵四边形ADEF是菱形 ‎∴AD=AF．‎ ‎∴△ABD≌△ACF ‎∴∠ADC=∠AFC 又∵∠ACB=∠ADC＋∠DAC，‎ ‎∴∠AFC=∠ACB－∠DAC ‎⑶补全图形如下图 A B C D F E ‎∠AFC、∠ACB、∠DAC之间的等量关系是 ‎∠AFC=2∠ACB－∠DAC ‎（或∠AFC＋∠DAC＋∠ACB=180°以及这两个等式的正确变式）．‎ 内蒙古巴彦淖尔 ‎24. （本题满分12分）‎ 如图，直线y=x+3与坐标轴分别交于A,B两点，抛物线y=ax2+bx‎-3a经过点A,B，顶点为C，连接CB并延长交x轴于点E，点D与点B关于抛物线的对称轴MN对称。‎ （1） 求抛物线的解析式及顶点C的坐标；‎ （2） 求证：四边形ABCD是直角梯形。‎ ‎（1）由与坐标轴分别交与A、B两点，易得A点坐标（-3，0）、‎ B点坐标（0，3）‎ 抛物线经过A、B两点 ‎ ‎ ‎ 得： ‎ 抛物线解析式为：‎ 顶点C的坐标为（-1，4）‎ ‎（2）B、D关于MN对称，C（-1，4），B（0，3）‎ D（-2，3）‎ ‎[来源:学科网]‎ OA=‎OB 又 B、D关于MN对称 ‎ ‎ 又轴 ‎//X轴 ‎[来源:学科网]‎ 关于MN对称 CD//AB 又AD与BC不平行 四边形ABCD是梯形 四边形ABCD是直角梯形 内蒙古包头 ‎25、（2011•包头）如图，已知∠ABC=90°，AB=BC．直线l与以BC为直径的圆O相切于点C．点F是圆O上异于B、C的动点，直线BF与l相交于点E，过点F作AF的垂线交直线BC与点D．‎ ‎（1）如果BE=15，CE=9，求EF的长；‎ ‎（2）证明：①△CDF∽△BAF；②CD=CE；‎ ‎（3）探求动点F在什么位置时，相应的点D位于线段BC的延长线上，且使BC=CD，请说明你的理由．‎ 考点：相似三角形的判定与性质；勾股定理；圆周角定理；切线的性质；解直角三角形。‎ 分析：（1）由直线l与以BC为直径的圆O相切于点C，即可得∠BCE=90°，∠BFC=∠CFE=90°，则可证得△CEF∽△BEC，然后根据相似三角形的对应边成比例，即可求得EF的长；‎ ‎（2）①由∠FCD+∠FBC=90°，∠ABF+∠FBC=90°，根据同角的余角相等，即可得∠ABF=∠FCD，同理可得∠AFB=∠CFD，则可证得△CDF∽△BAF；‎ ‎②由△CDF∽△BAF与△CEF∽△BCF，根据相似三角形的对应边成比例，易证得，又由AB=BC，即可证得CD=CE；‎ ‎（3）由CE=CD，可得BC=CD=CE，然后在Rt△BCE中，求得tan∠CBE的值，即可求得∠CBE的度数，则可得F在⊙O的下半圆上，且=．‎ 解答：解：（1）∵直线l与以BC为直径的圆O相切于点C．‎ ‎∴∠BCE=90°，‎ 又∵BC为直径，‎ ‎∴∠BFC=∠CFE=90°，‎ ‎∵∠FEC=∠CEB，‎ ‎∴△CEF∽△BEC，‎ ‎∴，‎ ‎∵BE=15，CE=9，‎ 即：，‎ 解得：EF=；‎ ‎（2）证明：①∵∠FCD+∠FBC=90°，∠ABF+∠FBC=90°，‎ ‎∴∠ABF=∠FCD，‎ 同理：∠AFB=∠CFD，‎ ‎∴△CDF∽△BAF；‎ ‎②∵△CDF∽△BAF，‎ ‎∴，‎ 又∵△CEF∽△BCF，‎ ‎∴，‎ ‎∴，‎ 又∵AB=BC，‎ ‎∴CE=CD；‎ ‎（3）∵CE=CD，‎ ‎∴BC=CD=CE，‎ 在Rt△BCE中，tan∠CBE=，‎ ‎∴∠CBE=30°，‎ 故为60°，‎ ‎∴F在⊙O的下半圆上，且=．‎ 点评：此题考查了相似三角形的判定与性质，圆的切线的性质，圆周角的性质以及三角函数的性质等知识．此题综合性很强，解题的关键是方程思想与数形结合思想的应用．‎ 内蒙古呼和浩特 ‎24、（8分）如图所示，AC为⊙O的直径且PA⊥AC，BC是⊙O的一条弦，直线PB交直线AC于点D，.‎ ‎（1）求证：直线PB是⊙O的切线；（2）求cos∠BCA的值 ‎24、（1）证明：连接OB、OP ………………………………………………………（1分）‎ ‎∵ 且∠D=∠D ∴ △BDC∽△PDO ‎∴ ∠DBC=∠DPO ∴ BC∥OP ∴ ∠BCO=∠POA ∠CBO=∠BOP ‎∵ OB=OC ∴ ∠OCB=∠CBO ∴ ∠BOP=∠POA 又∵ OB=OA OP=OP ∴ △BOP≌△AOP ∴ ∠PBO=∠PAO 又∵ PA⊥AC ∴ ∠PBO=90°‎ ‎∴ 直线PB是⊙O的切线 …………………………………（4分）‎ ‎（2）由（1）知∠BCO=∠POA 设PB，则 又∵ ∴ ‎ 又∵ BC∥OP ∴ ‎ ‎∴ ∴ ∴ ‎ ‎∴ cos∠BCA=cos∠POA= ……………………………………………（8分）‎ 内蒙古乌兰察布 ‎23，（本小题10 分），某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A、B两种园艺造型共50个，摆放在迎宾大道两侧．已知搭配一个A种造型需甲种花卉8盆，乙种花卉4盆；搭配一个B种造型需甲种花卉5盆，乙种花卉9盆．‎ ‎(l）某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来；‎ ‎(2）若搭配一个A种造型的成本是200元，搭配一个B种造型的成本是360元，试说明（1）中哪种方案成本最低，最低成本是多少元？‎ ‎23，解：（1）设搭配A种造型个，则搭配B种造型个，得 解得：‎ ‎∵为正整数，‎ ‎∴可以取29,30,31,32,33.‎ ‎∴共有五种方案：‎ 方案一：A：29，B：21；‎ 方案二：A：30，B：20；‎ 方案三：A：31，B：19；‎ 方案四：A：32，B：18；‎ 方案五：A：33，B：17；‎ ‎（2）设费用为y，则 ‎∵，∴y随x的增大而减小，‎ ‎∴当时，即方案五的成本最低，最低成本=。‎ 宁夏 ‎25、（2011•宁夏）甲、乙两人分别乘不同的冲锋舟同时从A地逆流而上前往B地．甲所乘冲锋舟在静水中的速度为千米/分钟，甲到达B地立即返回．乙所乘冲锋舟在在静水中的速度为千米/分钟．已知A、B两地的距离为20千米，水流速度为千米/分钟，甲、乙乘冲锋舟行驶的距离y（千米） 与所用时间x（分钟）之间的函数图象如图所示．‎ ‎（1）求甲所乘冲锋舟在行驶的整个过程中，y与x之间的函数关系式．‎ ‎（2）甲、乙两人同时出发后，经过多少分钟相遇？．‎ 考点：一次函数的应用。‎ 分析：（1）分别求出甲乙两人的速度，依据路程=速度×时间，即可列出函数解析式；‎ ‎（2）解乙的函数解析式与甲由B到A的函数解析式组成的方程组即可．‎ 解答：解：（1）甲由A到B时的函数解析式是：y=（﹣）x，即y=x；‎ 甲到达B所用时间是：20÷（﹣）=24分钟，‎ 甲由B到A所用时间是：20÷（+）=20分钟，‎ ‎∴设由B到A函数解析式是：y=kx+b，‎ ‎∵点（24，20）与（44，0）在此函数图象上，‎ ‎∴，解得：，‎ ‎∴由B到A函数解析式是：y=﹣x+44，‎ ‎（2）甲由A到B时的函数解析式是：y=（﹣）x，即y=x；‎ 根据题意得：，解得：x=，则经过小时相遇．‎ 点评：本题主要考查了一次函数的应用，以及函数交点坐标的求法，正确写出函数解析式是解题的关键．‎ 青海省 ‎27. （2011年青海，27,10分）认真阅读下面关于三角形内外角平分线所夹的探究片段，完成所提出的问题.‎ 探究1：如图11-1，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90°+,理由如下:‎ ‎∵BO和CO分别是∠ABC和∠ACB的角平分线 探究2：如图11-2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由.‎ 探究3：如图11-3中，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？（只写结论，不需证明）‎ 结论： .‎ ‎【答案】‎ （1） 探究2结论：∠BOC=‎ 理由如下：‎ ‎∵ BO和CO分别是∠ABC和∠ACD的角平分线 ‎∴‎ ‎（2）探究3：结论∠BOC=90°－‎ 山东省滨州 ‎24.（本小题满分10分）‎ ‎（2011山东滨州，24，10分）如图，在△ABC中，点O是AC边上（端点除外）的一个动点，过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F，连接AE、AF。那么当点O运动到何下时，四边形AECF是矩形？并证明你的结论。‎ ‎【答案】‎ 当点O运动到AC的中点（或OA=OC）时，‎ 四边形AECF是矩形………………2分 证明：∵CE平分∠BCA,∴∠1=∠2，………………3分 又∵MN∥BC, ∴∠1=∠3，‎ ‎∴∠3=∠2，∴EO=CO. ………………5分 同理，FO=CO………………6分 ‎∴EO=FO 又OA=OC, ∴四边形AECF是平行四边形………………7分 又∵∠1=∠2，∠4=∠5，‎ ‎∴∠1+∠5=∠2+∠4. ………………8分 A B C O D 又∵∠1+∠5+∠2+∠4=180°‎ ‎∴∠2+∠4=90°………………9分 ‎∴四边形AECF是矩形………………10分 山东省德州市 ‎22． (本题满分10分) ‎ ‎●观察计算 当，时， 与的大小关系是__________．‎ 当，时， 与的大小关系是__________．‎ ‎●探究证明 如图所示，为圆O的内接三角形，为直径，过C作于D，设，BD=b．‎ ‎（1）分别用表示线段OC，CD；‎ ‎（2）探求OC与CD表达式之间存在的关系（用含a，b的式子表示）．‎ ‎●归纳结论 根据上面的观察计算、探究证明，你能得出与的大小关系是：____________．‎ ‎●实践应用 要制作面积为‎1平方米的长方形镜框，直接利用探究得出的结论，求出镜框周长的最小值．‎ ‎22．（本题满分10分）‎ ‎●观察计算:>， =. …………………2分 ‎●探究证明：‎ ‎（1），‎ A B C O D ‎∴…………………3分 AB为⊙O直径,‎ ‎∴.‎ ‎，，‎ ‎ ∴∠A=∠BCD.‎ ‎∴△∽△. …………………4分 ‎∴.‎ 即,‎ ‎∴. …………………5分 ‎（2）当时,, =；‎ 时,, >．…………………6分 ‎●结论归纳: ． ………………7分 ‎●实践应用 设长方形一边长为米,则另一边长为米,设镜框周长为l米，则 ‎ ≥ ． ……………9分 当,即（米）时,镜框周长最小．‎ 此时四边形为正方形时,周长最小为‎4 米.……………10分 山东省东营 ‎23、（2011•东营）在平面直角坐标系中，现将一块等腰直角三角板放在第一象限，斜靠在两坐标轴上，且点A（0，2），点C（1，0），如图所示，抛物线经过点B．‎ ‎（1）求点B的坐标；‎ ‎（2）求抛物线的解析式；‎ ‎（3）在抛物线上是否还存在点P（点B除外），使△ACP仍然是以AC为直角边的等腰直 角三角形？若存在，求所有点P的坐标；若不存在，请说明理由．‎ 考点：二次函数综合题。‎ 专题：代数几何综合题；分类讨论；方程思想。‎ 分析：（1）首先过点B作BD⊥x轴，垂足为D，易证得△BDC≌△CAO，即可得BD=OC=1，CD=OA=2，则可求得点B的坐标；‎ ‎（2）利用待定系数法即可求得二次函数的解析式；‎ ‎（3）分别从①以AC为直角边，点C为直角顶点，则延长BC至点P1使得P‎1C=BC，得到等腰直角三角形ACP1，过点P1作P‎1M⊥x轴，②若以AC为直角边，点A为直角顶点，则过点A作AP2⊥CA，且使得AP2=AC，得到等腰直角三角形ACP2，过点P2作P2N⊥y轴，③若以AC为直角边，点A为直角顶点，则过点A作AP3⊥CA，且使得AP3=AC，得到等腰直角三角形ACP3，过点P3作P3H⊥y轴，去分析则可求得答案．‎ 解答：（1）过点B作BD⊥x轴，垂足为D，∵∠BCD+∠ACO=90° ，∠ACO+∠OAC =90°；‎ ‎∴∠BCD=∠CAO； 又∵∠BDC=∠COA=90°；CB=AC，‎ ‎∴ △BDC≌△CAO=90°，∴BD=OC=1，CD=OA=2；∴点B的坐标为(3,1)‎ ‎（2）抛物线经过点B(3,1)，则得 解得，所以抛物线的解析式为 ‎（3）假设存在点P，似的△ACP是直角三角形:‎ ‎①若以AC为直角边，点C为直角顶点；则延长BC至点P1 使得P‎1C=BC,得到等腰直角三角形ACP1，过点P1作P‎1M⊥x轴，如图（1）。‎ ‎∵CP1=BC，∠MCP1=∠BCD， ∠P1MC=∠BDC=90°，∴△MCP1≌△BCD ‎∴ CM=CD=2，P‎1M=BD=1，可求得点P1（-1，-1）；经检验点P1（-1，-1）在抛物线为上； ‎ ‎②若以AC为直角边， 点A为直角顶点；则过点A作AP2⊥CA，且使得AP2=AC，得到等腰直角三角形ACP2，过点P2作P2N⊥y轴，如图（2）。同理可得△AP2N≌△CAO；∴NP2=OA=2，AN=OC=1，可求得点P2（-2，1），；经检验点P2（-2，1）也在抛物线上；‎ ‎③若以AC为直角边， 点A为直角顶点；则过点A作AP3⊥CA，且使得AP3=AC，得到等腰直角三角形ACP3，过点P3作P3H⊥y轴，如图（3）同理可得△AP3H≌△CAO；∴HP3=OA=2，AH=OC=1，可求得点P3（2，3），；经检验点P3（2，3）不抛物线上；‎ 故符合条件的点有P1（-1，-1），P2（-2，1）两个。‎ 点评：此题考查了全等三角形的判定与性质，待定系数法求二次函数的解析式，等腰直角三角形的性质等知识．此题综合性和强，难度较大，解题的关键是要注意数形结合思想、方程思想与分类讨论思想的应用的应用．‎ 山东省济南 ‎27、（2011•济南）如图，矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线y=﹣x2+bx+c经过A、C两点，与AB边交于点D．‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S．‎ ‎①求S关于m的函数表达式，并求出m为何值时，S取得最大值；‎ ‎②当S最大时，在抛物线y=﹣x2‎ ‎+bx+c的对称轴l上若存在点F，使△FDQ为直角三角形，请直接写出所有符合条件的F的坐标；若不存在，请说明理由．‎ 考点：二次函数综合题。‎ 专题：代数几何综合题；数形结合。‎ 分析：（1）将A、C两点坐标代入抛物线y=﹣x2+bx+c，即可求得抛物线的解析式；‎ ‎（2）①先用m 表示出QE的长度，进而求出三角形的面积S关于m的函数，化简为顶点式，便可求出S的最大值；‎ ‎②直接写出满足条件的F点的坐标即可，注意不要漏写．‎ 解答：解：（1）将A、C两点坐标代入抛物线y=﹣x2+bx+c，，‎ 解得，‎ ‎∴抛物线的解析式为y=﹣x2+x+8；‎ ‎（2）①∵OA=8，OC=6‎ ‎∴AC==10，‎ 过点Q作QE⊥BC与E点，则sin∠ACB===，‎ ‎∴=，‎ ‎∴QE=（10﹣m），‎ ‎∴S=•CP•QE=m×（10﹣m）=m2+‎3m=（m﹣5）2+，‎ ‎∴当m=5时，S取最大值；‎ ‎②在抛物线对称轴l上存在点F，使△FDQ为直角三角形，‎ 满足条件的点F共有四个，坐标分别为 F1（，8），F2（，4），F3（，6+2），F4（，6﹣2），‎ 点评：本题是二次函数的综合题，其中涉及的到的知识点有抛物线的公式的求法抛物线的最值等知识点，是各地中考的热点和难点，，解题时注意数形结合数学思想的运用，同学们要加强训练，属于中档题．‎ 山东济宁 ‎22、（8分）（2011·济宁）去冬今春，济宁市遭遇了200年不遇的大旱，某乡镇为了解决抗旱问题，要在某河道建一座水泵站，分别向河的同一侧张村A和李村B送水。经实地勘查后，工程人员设计图纸时，以河道上的大桥O为坐标原点，以河道所在的直线为x轴建立直角坐标系（如图）。两村的坐标分别为A（2，3），B（12，7）。‎ ‎(1)、若从节约经费考虑，水泵站建在距离大桥O多远的 地方可使所用输水管道最短？‎ ‎(2)、水泵站建在距离大桥O多远的地方，可使它到张村、李村的 距离相等？‎ ‎22、解：（1）作点B关于x轴的对成点E，连接AE，则点E为（12，-7）‎ ‎ 设直线AE的函数关系式为y=kx+b,则 ‎ 2k+b=3 ‎ ‎12k+b=-7 ‎ 解得 k=-1‎ ‎ b=5 ‎ 当y=0时， x=5‎ 所以，水泵站建在距离大桥‎5千米的地方，可使所用输水管道最短。‎ ‎（2）作线段AB的垂直平分线GF，交AB于点F，交x轴欲点G 设点G的坐标为（x，0）‎ 在Rt△AGD中，AG2=AD2+DG2=32+(x-2)2‎ 在Rt△BCG中，BG2=BC2+GC2=72+(12-x)2‎ ‎∵AG=BG ∴32+(x-2)2=72+(12-x)2 解得 x=9‎ 所以 ，水泵站建在距离大桥‎9千米的地方，可使它到张村、李村的距离相等。‎ F G E C B A D ‎/km ‎/km ‎2 4 6 8 10 12‎ ‎8‎ ‎6‎ ‎4‎ ‎2‎ 第22题 山东省临沂 ‎25、（2011•临沂）如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角扳的一边交CD于点F．另一边交CB的延长线于点G．‎ ‎（1）求证：EF=EG；‎ ‎（2）如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由：‎ ‎（3）如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB=a、BC=b，求的值．‎ 考点：相似三角形的判定与性质；全等三角形的判定与性质；矩形的性质；正方形的性质。‎ 分析：（1）由∠GEB+∠BEF=90°，∠DEF+∠BEF=90°，可得∠DEF=∠GEB，又由正方形的性质，可利用SAS证得Rt△FED≌Rt△GEB，则问题得证；‎ ‎（2）首先点E分别作BC、CD的垂线，垂足分别为H、I，然后利用SAS证得Rt△FEI≌Rt△GEH，则问题得证；‎ ‎（3）首先过点E分别作BC、CD的垂线，垂足分别为M、N，易证得EM∥AB，EN∥AD，则可证得△CEN∽△CAD，△CEM∽△CAB，又由有两角对应相等的三角形相似，证得△GME∽△FNE，根据相似三角形的对应边成比例，即可求得答案．‎ 解答：（1）证明：∵∠GEB+∠BEF=90°，∠DEF+∠BEF=90°，∴∠DEF=∠GEB，‎ 又∵ED=BE，∴Rt△FED≌Rt△GEB，∴EF=EG；‎ ‎（2）成立．‎ 证明：如图，过点E分别作BC、CD的垂线，垂足分别为H、I，‎ 则EH=EI，∠HEI=90°，‎ ‎∵∠GEH+∠HEF=90°，∠IEF+∠HEF=90°，∴∠IEF=∠GEH，∴Rt△FEI≌Rt△GEH，∴EF=EG；‎ ‎（3）解：如图，过点E分别作BC、CD的垂线，垂足分别为M、N，则∠MEN=90°，‎ ‎∴EM∥AB，EN∥AD．∴△CEN∽△CAD，△CEM∽△CAB，‎ ‎∴，，‎ ‎∴，即=，‎ ‎∵∠IEF+∠FEM=∠GEM+∠FEM=90°，‎ ‎∴∠GEM=∠FEN，‎ ‎∵∠GME=∠FNE=90°，‎ ‎∴△GME∽△FNE，‎ ‎∴，∴．‎ 点评：此题考查了正方形，矩形的性质，以及全等三角形与相似三角形的判定与性质．此题综合性较强，注意数形结合思想的应用．‎ 山东省青岛 问题提出 我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，而解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一．所谓“作差法”：就是通过作差、变形，并利用差的符号确定他们的大小，即要比较代数式M、N的大小，只要作出它们的差M－N，若M－N＞0，则M＞N；若M－N＝0，则M＝N；若M－N＜0，则M＜N．‎ 问题解决 a a a a b b b b 图1‎ 如图1，把边长为a＋b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形，试比较两个小正方形面积之和M与两个矩形面积之和N的大小．‎ 解：由图可知：M＝a2＋b2，N＝2ab．‎ ‎∴M－N＝a2＋b2－2ab＝(a－b)2．‎ ‎∵a≠b，∴(a－b)2＞0．‎ ‎∴M－N＞0．‎ ‎∴M＞N．‎ 类别应用 ‎(1)已知小丽和小颖购买同一种商品的平均价格分别为元/千克和元/千克(a、b是正数，且a≠b)，试比较小丽和小颖所购买商品的平均价格的高低．‎ ‎ (2)试比较图2和图3中两个矩形周长M1、N1的大小(b＞c)．‎ 图3‎ a＋b b＋‎‎3c b＋c a－c 图2‎ 联系拓广 小刚在超市里买了一些物品，用一个长方体的箱子“打包”，这个箱子的尺寸如图4所示(其中b＞a＞c＞0)，售货员分别可按图5、图6、图7三种方法进行捆绑，吻哪种方法用绳最短？哪种方法用绳最长？请说明理由．‎ 图4‎ 图5‎ 图6‎ 图7‎ a b c ‎23.解：类比应用 ‎ （1）‎ ‎ ∵是正整数且 ‎∴， ∴‎ 即效力的平均价格比小颖的高。‎ ‎（2）由图知，‎ ‎ ‎ ‎∵，∴，即，∴。‎ ‎∴第一个矩形的周长大于第二个矩形的周长。‎ ‎ 联系拓广 ‎ 设图⑤的捆绑绳长为，则 ‎ 设图⑥的捆绑绳长为，则 设图⑦的捆绑绳长为，则 ‎∴‎ ‎∴（由式子观察得出，也可得分。）‎ ‎∵，∴，即，∴‎ ‎∴所以第三种捆绑方法用绳最长，第二种最短。‎ 山东省日照 ‎ ‎23．（本题满分10分）如图，已知点D为等腰直角△ABC内一点，∠CAD＝∠CBD＝15°，E为AD延长线上的一点，且CE＝CA．‎ ‎（1）求证：DE平分∠BDC；（2）若点M在DE上，且DC=DM，求证： ME=BD．‎ ‎23．（本题满分10分）‎ ‎ 证明：（1）在等腰直角△ABC中，‎ ‎∵∠CAD=∠CBD=15o，‎ ‎∴∠BAD=∠ABD=45o-15o=30o，‎ ‎∴BD=AD，∴△BDC≌△ADC， ‎ ‎∴∠DCA=∠DCB=45o．………………2分 由∠BDM=∠ABD+∠BAD=30o+30o=60o，‎ ‎∠EDC=∠DAC+∠DCA=15o+45o=60o，‎ ‎∴∠BDM=∠EDC，‎ ‎∴DE平分∠BDC； ……………4分 ‎（2）如图，连接MC，‎ ‎∵DC=DM，且∠MDC=60°，‎ ‎∴△MDC是等边三角形，即CM=CD． ‎ 又∵∠EMC=180°-∠DMC=180°-60°=120°，‎ ‎∠ADC=180°-∠MDC=180°-60°=120°，‎ ‎∴∠EMC=∠ADC． …………………………7分 又∵CE=CA，‎ ‎∴∠DAC=∠CEM=15°，∴△ADC≌△EMC， ………………………9分 ‎∴ME=AD=DB． ………………………………10分 山东省威海 ‎24、（2011•威海）如图，ABCD是一张矩形纸片，AD=BC=1，AB=CD=5．在矩形ABCD的边AB上取一点M，在CD上取一点N，将纸片沿MN折叠，使MB与DN交于点K，得到△MNK．‎ ‎（1）若∠1=70°，求∠MKN的度数；‎ ‎（2）△MNK的面积能否小于？若能，求出此时∠1的度数；若不能，试说明理由；‎ ‎（3）如何折叠能够使△MNK的面积最大？请你用备用图探究可能出现的情况，求最大值．‎ 考点：翻折变换（折叠问题）；勾股定理；矩形的性质。‎ 专题：综合题；分类讨论。‎ 分析：（1）根据矩形的性质和折叠的性质求出∠KNM，∠KMN的度数，根据三角形内角和即可求解；‎ ‎（2）过M点作ME⊥DN，垂足为E，通过证明NK≥1，由三角形面积公式可得△MNK的面积不可能小于；‎ ‎（3）分情况一：将矩形纸片对折，使点B与D重合，此时点K也与D重合；情况二：将矩形纸片沿对角线AC对折，此时折痕即为AC两种情况讨论求解．‎ 解答：解：（1）∵ABCD是矩形，‎ ‎∴AM∥DN．‎ ‎∴∠KNM=∠1．‎ ‎∵∠1=70°，‎ ‎∴∠KNM=∠KMN=70°，‎ ‎∴∠MKN=40°．‎ ‎（2）不能．‎ 过M点作ME⊥DN，垂足为E，则ME=AD=1．‎ ‎∵∠KNM=∠KMN，‎ ‎∴MK=NK，‎ 又MK≥ME，‎ ‎∴NK≥1．‎ ‎∴△MNK的面积=NK•ME≥．‎ ‎∴△MNK的面积不可能小于．‎ ‎（3）分两种情况：‎ 情况一：将矩形纸片对折，使点B与D重合，此时点K也与D重合．‎ MK=MD=x，则AM=5﹣x．‎ 由勾股定理得12+（5﹣x）2=x2，‎ 解得x=2.6．‎ ‎∴MD=ND=2.6．‎ S△MNK=S△MND==1.3．‎ 情况二：将矩形纸片沿对角线AC对折，此时折痕即为AC．‎ MK=AK=CK=x，则DK=5﹣x．‎ 同理可得MK=NK=2.6．‎ ‎∵MD=1‎ ‎∴S△MNK=S△MND==1.3．‎ ‎△MNK的面积最大值为1.3．‎ 点评：本题考查了翻折变换（折叠问题），矩形的性质，勾股定理，三角形的面积计算，注意分类思想的运用，综合性较强，有一点的难度．‎ 山东省潍坊 ‎23、（2011•潍坊）如图，AB是半径O的直径，AB=2．射线AM、BN为半圆O的切线．在AM上取一点D，连接BD交半圆于点C，连接AC．过O点作BC的垂线OE，垂足为点E，与BN相交于点F．过D点作半圆O的切线DP，切点为P，与BN相交于点Q．‎ ‎（1）求证：△ABC∽△OFB；‎ ‎（2）当△ABD与△BFO的面枳相等时，求BQ的长；‎ ‎（3）求证：当D在AM上移动时（A点除外），点Q始终是线段BF的中点．‎ 考点：切线的性质；全等三角形的判定与性质；勾股定理；圆周角定理；相似三角形的判定与性质。‎ 专题：证明题；几何综合题。‎ 分析：（1）根据OE∥AC，得出∠BAC=∠FOB，进而得出∠BCA=∠FBO=90°，从而证明结论；‎ ‎（2）根据△ACB∽△OBF得出△ABD∽△BFO，从而得出DQ∥AB，即可得出BQ=AD；‎ ‎（3）首先得出AD=DP，QB=BQ，进而得出DQ2=QK2+DK2，得出BF=2BQ，即可得出Q为BF的中点．‎ 解答：证明：（1）∵AB为直径，‎ ‎∴∠ACB=90°，即：AC⊥BC，‎ 又OE⊥BC，‎ ‎∴OE∥AC，‎ ‎∴∠BAC=∠FOB，‎ ‎∵BN是半圆的切线，‎ ‎∴∠BCA=∠FBO=90°，‎ ‎∴△ACB∽△OBF．‎ 解：（2）由△ACB∽△OBF得，∠OFB=∠DBA，∠DAB=∠OBF=90°，‎ ‎∴△ABD∽△BFO，‎ 当△ABD与△BFO的面积相等时，△ABD≌△BFO，‎ ‎∴AD=1，‎ 又DPQ是半圆O的切线，‎ ‎∴OP=1，且OP⊥DP，‎ ‎∴DQ∥AB，‎ ‎∴BQ=AD=1，‎ ‎（3）由（2）知，△ABD∽△BFO，‎ ‎∴=，‎ ‎∴BF=，‎ ‎∵DPQ是半圆O的切线，‎ ‎∴AD=DP，QB=BQ，‎ 过Q点作AM的垂线QK，垂足为K，在直角三角形DQK中，‎ DQ2=QK2+DK2，‎ ‎∴（AD+BQ）2=（AD﹣BQ）2+22．‎ ‎∴BQ=，‎ ‎∴BF=2BQ，‎ ‎∴Q为BF的中点．‎ 点评：此题主要考查了切线的性质以及全等三角形的判定和相似三角形的判定等知识，熟练利用相似三角形的判定是解决问题的关键．‎ 山东省烟台 ‎25. （2011山东烟台，25，12分）‎ 已知：AB是⊙O的直径，弦CD⊥AB于点G，E是直线AB上一动点（不与点A、B、G重合），直线DE交⊙O于点F，直线CF交直线AB于点P.设⊙O的半径为r.‎ ‎（1）如图1，当点E在直径AB上时，试证明：OE·OP＝r2‎ ‎（2）当点E在AB（或BA）的延长线上时，以如图2点E的位置为例，请你画出符合题意的图形，标注上字母，（1）中的结论是否成立？请说明理由.‎ A B C D E F P ‎.‎ O G ‎（图1）‎ ‎.‎ A B C D E ‎.‎ O G ‎（图2）‎ ‎【解】（1）证明：连接FO并延长交⊙O于Q，连接DQ.‎ ‎∵FQ是⊙O直径，∴∠FDQ＝90°. ∴∠QFD＋∠Q＝90°. ‎ ‎∵CD⊥AB，∴∠P＋∠C＝90°.‎ ‎∵∠Q＝∠C，∴∠QFD＝∠P.‎ ‎∵∠FOE＝∠POF，∴△FOE∽△POF.‎ ‎∴.∴OE·OP＝OF2＝r2.‎ ‎（2）解：（1）中的结论成立.‎ 理由：如图2，依题意画出图形，连接FO并延长交⊙O于M，连接CM.‎ ‎∵FM是⊙O直径，∴∠FCM＝90°，∴∠M＋∠CFM＝90°.‎ ‎∵CD⊥AB，∴∠E＋∠D＝90°.‎ ‎∵∠M＝∠D，∴∠CFM＝∠E. ‎ ‎∵∠POF＝∠FOE，∴△POF∽△FOE.‎ ‎∴，∴OE·OP＝OF2＝r2.‎ ‎【思路分析】（1）要证等积式，需要将其化为比例式，再利用相似证明. 观察图形，此题显然要连半径OF，构造OE、OP所在的三角形， 这样问题便转化为证明△FOE∽△POF了. 而要证明△FOE∽△POF ‎，由于已经存在一个公共角，因此只需再证明另一角对应相等即可，这一点利用圆周角定理及其推论可获证，且方法不惟一；（2）同（1）类似.‎ ‎【方法规律】此题综合考查圆的性质及相似的知识，解题关键是辅助线的灵活添加. 值得注意的是（2）问是（1）知识的变式，能开拓视野，提高思维深度、灵敏性，其证明同（1）类似，可不必证明.‎ ‎【易错点分析】（1）不会添加辅助线；（2）证不出相似所需一角对应相等的条件. ‎ ‎【关键词】圆，圆周角定理，相似.‎ ‎【难度】★★★★☆‎ ‎【题型】证明题. ‎ 山东省淄博 ‎23．(9分)已知：ABCD的两边AB，AD的长是关于x的方程的两个实数根．‎ ‎（1）当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；‎ ‎（2）若AB的长为2，那么ABCD的周长是多少？‎ ‎【答案】解：（1）∵四边形ABCD是菱形，∴AB=AD。‎ 又∵，‎ 当，即m=1时，四边形ABCD是菱形。‎ 把m=1代入，得。‎ ‎∴。 ‎ ‎∴菱形ABCD的边长是。‎ ‎（2）把AB=2代入，得， 解得。‎ 把代入，得。 ‎ 解得，。∴AD=。‎ ‎∵四边形ABCD是平行四边形， ‎ ‎∴□ABCD的周长是2（2+）=5。‎ 山西省 ‎25．(本题9分)如图(1)，Rt△ABC中，∠ACB=-90°，CD⊥AB，垂足为D．AF平分∠CAB，交CD于点E，交CB于点F ‎（1）求证：CE=CF．‎ ‎（2）将图（1）中的△ADE沿AB向右平移到△A’D’E’的位置，使点E’落在BC边上，其它条件不变，如图（2）所示．试猜想：BE'与CF有怎样的数量关系?请证明你的结论．‎ ‎（1）证明：略 ‎（2）解：相等 证明：如图，过点E作EG⊥AC于G．‎ 又∵ AF平分∠CAB，ED⊥AB，∴ED=EG．‎ ‎ 由平移的性质可知：D’E’=DE，∴D’E’ =GE．‎ ‎ ∵∠ACB=90°． ∴∠ACD+∠DCB=90°‎ ‎ ∵CD⊥AB于D． ∴∠B+∠DCB=90°．∴ ∠ACD=∠B 在Rt△CEG与Rt△BE’D’中，∵∠GCE=∠B，∠CGE=∠BD’E’，CE=D’E’‎ ‎ ∴△CEG≌△BE’D’ ∴CE=BE’‎ ‎ 由（1）可知CE=CF，‎ 陕西省 ‎24、（2011•陕西）如图，二次函数的图象经过△AOB的三个顶点，其中A（﹣1，m），B（n，n）‎ ‎（1）求A、B的坐标；‎ ‎（2）在坐标平面上找点C，使以A、O、B、C为顶点的四边形是平行四边形．‎ ‎①这样的点C有几个？‎ ‎②能否将抛物线平移后经过A、C两点，若能，求出平移后经过A、C两点的一条抛物线的解析式；若不能，说明理由．‎ 考点：二次函数综合题。‎ 专题：代数几何综合题。‎ 分析：（1）把A（﹣1，m）代入函数式而解得m的值，同理解得n值，从而得到A，B的坐标；‎ ‎（2）①由题意可知：这样的C点有3个，‎ ‎②能，分别考虑函数图象经过三个点，从而得到函数方程．‎ 解答：解：（1）∵y=的图象过点A（﹣1，m）‎ ‎∴ 即m=1‎ 同理：n= 解之，得n=0（舍）或n=2‎ ‎∴A（﹣1，1），B（2，2）‎ ‎（2）①由题意可知：这样的C点有3个 ‎②能 当平移后的抛物线经过A、C1两个点时，将B点向左平移3个单位再向下平移1个单位．使点B移到A点，这时A、C1两点的抛物线的解析式为y+1= 即y= 附：另两条平移后抛物线的解析式分别为：‎ i）经过A、C2两点的抛物线的解析式为 ii）设经过A、C3两点的抛物线的解析式为，OC3可看作线段AB向右平移1个单位再向下平移1个单位得到∴C3（3，1）‎ 依题意，得解得 ‎∴经过A、C3两点的抛物线的解析式为 点评：本题考查了二次函数的综合运用，（1）把A（﹣1，m）代入函数式而解得；（2）①由题意可知点C有几个，②分别考虑函数图象经过三个点，从而得到函数方程．也从而确定能．本题有一定难度，在图象上做好辅助线，考虑全面，而不至于漏解．‎ 上海市 ‎24．（本题满分12分，）‎ 已知平面直角坐标系xOy（如图1），一次函数的图像与y轴交于点A，点M在正比例函数的图像上，且MO＝MA．二次函数y＝x2＋bx＋c的图像经过点A、M．‎ ‎（1）求线段AM的长；‎ ‎（2）求这个二次函数的解析式；‎ ‎（3）如果点B在y轴上，且位于点A下方，点C在上述二次函数的图像上，点D在一次函数的图像上，且四边形ABCD是菱形，求点C的坐标．‎ ‎24. [解] (1) 根据两点之间距离公式，设M(a, a)，由| MO |=| MA |, 解得：a=1，则M(1, ),‎ ‎ 即AM=。‎ ‎ (2) ∵ A(0, 3)，∴ c=3，将点M代入y=x2+bx+3，解得：b= -，即：y=x2-x+3。‎ ‎ (3) C(2, 2) (根据以AC、BD为对角线的菱形)。注意：A、B、C、D是按顺序的。‎ ‎ [解] 设B(0, m) (m<3)，C(n, n2-n+3)，D(n, n+3)，‎ ‎ | AB |=‎3-m，| DC |=yD-yC=n+3-(n2-n+3)=n-n2，‎ ‎ | AD |==n，‎ ‎ | AB |=| DC |Þ‎3-m=n-n2…j，| AB |=| AD |Þ‎3-m=n…k。‎ ‎ 解j，k，得n1=0(舍去)，或者n2=2，将n=2代入C(n, n2-n+3)，得C(2, 2)。‎ 四川省成都市 ‎27、（2011•成都）已知：如图，以矩形ABCD的对角线AC的中点O为圆心，OA长为半径作⊙O，⊙O经过B、D两点，过点B作BK⊥AC，垂足为K．过D作DH∥KB，DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H．‎ ‎（1）求证：AE=CK；‎ ‎（2）如果AB=a，AD=（a为大于零的常数），求BK的长：‎ ‎（3）若F是EG的中点，且DE=6，求⊙O的半径和GH的长．‎ 考点：相似三角形的判定与性质；全等三角形的判定与性质；三角形中位线定理；垂径定理；圆周角定理。‎ 专题：证明题；几何综合题。‎ 分析：（1）根据ABCD是矩形，求证△BKC≌△ADE即可；‎ ‎（2）根据勾股定理求得AC的长，再求证△BKC∽△ABC，利用其对应边成比例即可求得BK．‎ ‎（3）根据三角形中位线定理可求出EF，再利用△AFD≌△HBF可求出HF，然后即可求出GH；利用射影定理求出AE，再利△AED∽△HEC求证AE=AC，然后即可求得AC即可．‎ 解答：（1）证明：∵四边形据ABCD是矩形，‎ ‎∴AD=BC，‎ ‎∵BK⊥AC，DH∥KB，‎ ‎∴∠BKC=∠AED=90°，‎ ‎∴△BKC≌△ADE，‎ ‎∴AE=CK；‎ ‎（2）∵AB=a，AD==BC，‎ ‎∴AC=== ‎∵BK⊥AC，‎ ‎∴△BKC∽△ABC，‎ ‎∴=，‎ ‎∴=，‎ ‎∴BK=a，‎ ‎∴BK=a．‎ ‎（3）连接OF，‎ ‎∵ABCD为矩形，‎ ‎∴=，‎ ‎∴EF=ED=×6=3，‎ ‎∵F是EG的中点，‎ ‎∴GF=EF=3，‎ ‎∵△AFD≌△HBF，‎ ‎∴HF=FE=3+6=9，‎ ‎∴GH=6，‎ ‎∵DH∥KB，ABCD为矩形，‎ ‎∴AE2=EF•ED=3×6=18，‎ ‎∴AE=3，‎ ‎∵△AED∽△HEC，‎ ‎∴==，‎ ‎∴AE=AC，‎ ‎∴AC=9，‎ 则AO=．‎ 点评：此题主要考查相似三角形的判定与性质，全等三角形的判定与性质，三角形中位线定理，垂径定理，圆周角定理等知识点，综合性很强，利用学生系统的掌握知识，是一道很典型的题目．‎ 四川省达州 ‎22、（7分）我市化工园区一化工厂，组织20辆汽车装运A、B、C三种化学物资共200吨到某地．按计划20辆汽车都要装运，每辆汽车只能装运同一种物资且必须装满．请结合表中提供的信息，解答下列问题:‎ ‎（1）设装运A种物资的车辆数为，装运B种物资的车辆数为．求与的函数关系式；‎ ‎（2）如果装运A种物资的车辆数不少于5辆，装运B种物资的车辆数不少于4辆， 那么车辆的安排有几种方案?并写出每种安排方案；‎ ‎（3）在（2）的条件下，若要求总运费最少，应采用哪种安排方案?请求出最少总运费．‎ 物资种类 A B C 每辆汽车运载量（吨）‎ ‎12‎ ‎10‎ ‎8‎ 每吨所需运费（元/吨）‎ ‎240‎ ‎320‎ ‎200‎ ‎22、（7分）解：（1）根据题意，得：‎ ‎∴……………………2分 ‎（2）根据题意，得：‎ ‎ 解之得：‎ ‎∵取正整数，∴5，6，7，8……………………4分 ‎∴共有4种方案，即 A B C 方案一 ‎5‎ ‎10‎ ‎5‎ 方案二 ‎6‎ ‎8‎ ‎6‎ 方案三 ‎7‎ ‎6‎ ‎7‎ 方案四 ‎8‎ ‎4‎ ‎8‎ ‎……………………5分 ‎（3）设总运费为M元，‎ 则M=‎ 即：M=‎ ‎∵M是的一次函数，且M随增大而减小，‎ ‎∴当=8时，M最小，最少为48640元……………………7分 四川省广安 ‎ ‎29、如图所示，P是⊙O外一点，PA是⊙O的切线，A是切点，B是⊙O 上一点，且PA=PB，连接AO、BO、AB，并延长BO与切线PA相交于点Q．‎ ‎（1）求证：PB是⊙O的切线；‎ ‎（2）求证：AQ•PQ=OQ•BQ；‎ ‎（3）设∠AOQ=α，若cosα= ，OQ=15，求AB的长．‎ ‎29. 解：（1）证明：连接OP，与AB交与点C．‎ ‎∵PA=PB，OA=OB，OP=OP，‎ ‎∴△OAP≌△OBP（SSS），‎ ‎∴∠OBP=∠OAP，‎ ‎∵PA是⊙O的切线，A是切点，‎ ‎∴∠OAP=90°，‎ ‎∴∠OBP=90°，即PB是⊙O的切线；‎ ‎（2）∵∠Q=∠Q，∠OAQ=∠QBP=90°，‎ ‎∴△QAO∽△QBP，‎ ‎∴ ，即AQ•PQ=OQ•BQ；‎ ‎（3）在Rt△OAQ中，∵OQ=15，cosα=，‎ ‎∴OA=12，AQ=9，∴QB=27；‎ ‎∵ = ，∴PQ=45，即PA=36，‎ ‎∴OP=；‎ ‎∵PA、PB是⊙O的切线，∴OP⊥AB，AC=BC，‎ ‎∴PA•OA=OP•AC，即36×12=•AC，‎ ‎∴AC=，故AB=．‎ 四川省乐山 ‎ ‎25．如图（1）,在直角△ABC中, ∠ACB=90,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F,若AC=mBC,CE=nEA(m,n为实数).‎ 试探究线段EF与EG的数量关系.‎ (1) 如图（2）,当m=1,n=1时,EF与EG的数量关系是 ‎ 证明:‎ (2) ‎ 如图（3）,当m=1,n为任意实数时,EF与EG的数量关系是 ‎ 证明 (3) 如图（1）,当m,n均为任意实数时,EF与EG的数量关系是 ‎ ‎(写出关系式,不必证明)‎ ‎25. （1）图甲：连接DE，‎ ‎∵AC=mBC，CD⊥AB，当m=1，n=1时 ‎∴AD=BD，∠ACD=45°，‎ ‎∴CD=AD=AB，‎ ‎∵AE=nEC，‎ ‎∴DE=AE=EC=AC，‎ ‎∴∠EDC=45°，DE⊥AC，‎ ‎∵∠A=45°，‎ ‎∴∠A=∠EDG，‎ ‎∵EF⊥BE，‎ ‎∵∠AEF+∠FED=∠EFD+∠DEG=90°，‎ ‎∴∠AEF=∠DEG，‎ ‎∴△AEF≌△DEG（ASA），‎ ‎∴EF=EG．‎ ‎（2）解：EF=EG证明：作EM⊥AB于点M，EN⊥CD于点N，‎ ‎∵EM∥CD，‎ ‎∴△AEM∽△ACD，‎ ‎∴‎ 即EM=CD，‎ 同理可得，EN=AD，‎ ‎∵∠ACB=90°，CD⊥AB，‎ ‎∴tanA=，‎ ‎∴，‎ 又∵EM⊥AB，EN⊥CD，‎ ‎∴∠EMF=∠ENG=90°，‎ ‎∵EF⊥BE，‎ ‎∴∠FEM=∠GEN，‎ ‎∴△EFM∽△EGN，‎ ‎∴，‎ 即EF=EG；‎ ‎（3）EF=EG．‎ 四川省凉山 1． 如图，已知，以为直径，为圆心的半圆交于点，点为的中点，连接交于点，为的角平分线，且，垂足为点。‎ B D O H C E M F A ‎27题图 （1） 求证：是半圆的切线；‎ （2） 若，，求的长。‎ ‎27．（1）证明：连接，‎ ‎ ∵是直径， ∴，‎ ‎ 又∵于， ∴，‎ B D O H C EA M F A ‎27题图 ‎1‎ ‎2‎ ‎3‎ ‎7‎ ‎6‎ ‎5‎ ‎4‎ ‎ ∵ ∴。 ······························1分 ‎ ∵是的角平分线，‎ ‎ ∴。 ····················…2分 ‎ 又 ∵为的中点，‎ ‎ ∴ 。 ·····················3分 ‎ ∵于，‎ ‎ ∵， 即。‎ ‎ 又∵是直径， ∴是半圆的切线 ···4分 ‎（2）∵，。‎ 由（1）知，，∴。·····················5分 在中，于，平分，‎ ‎∴，∴。········································6分 由∽，得。········································7分 ‎∴，∴。················8分 四川省泸州 ‎26. （2011四川泸州，26，7分）如图，点P为等边△ABC外接圆劣弧BC上一点．‎ ‎（1）求∠BPC的度数；‎ ‎（2）求证：PA=PB+PC；‎ ‎（3）设PA，BC交于点M，若AB=4，PC=2，求CM的长度．‎ 答案：解：（1）∵△ABC为等边三角形，∴∠BAC=60°，‎ ‎∵点P为等边△ABC外接圆劣弧BC上一点，∴∠BPC+∠BAC=180°，∴∠BPC=120°，‎ ‎（2）在PA上截取PD=PC，‎ ‎∵AB=AC=BC，∴∠APB=∠APC=60°，∴△PCD为等边三角形，∴∠ADC=120°，‎ ‎∴△ACD≌△BCP，∴AD=PB，∴PA=PB+PC；‎ ‎（3）∵△CDM∽△ACM，∴CM：AM=DM：MC=DC：AC=2：4=1：2，‎ 设DM=x，则CM=2x，BM=4-2x，PM=2-x，AM=4x，∵△BPM∽△ACM，∴BP：AC=PM：CM，‎ 即3x：4=（2-x）：2x，解得，x=（舍去负号），则x=，∴CM= ．‎ 四川省眉山 ‎25、（2011•眉山）如图，点P是菱形ABCD的对角线BD上一点，连接CP并延长，交AD于E，交BA的延长线于F．‎ ‎（1）求证：∠DCP=∠DAP；‎ ‎（2）若AB=2，DP：PB=1：2，且PA⊥BF，求对角线BD的长．‎ 考点：相似三角形的判定与性质；全等三角形的判定与性质；勾股定理；菱形的性质。‎ 专题：计算题。‎ 分析：（1）根据菱形的性质得CD=AD，∠CDP=∠ADP，证明△CDP≌△ADP即可；‎ ‎（2）由菱形的性质得CD∥BA，可证△CPD∽△FPB，利用相似比，结合已知DP：PB=1：2，CD=BA，可证A为BF的中点，又PA⊥BF，从而得出PB=PF，已证PA=CP，把问题转化到Rt△PAB中，由勾股定理，列方程求解．‎ 解答：（1）证明：∵四边形ABCD为菱形，‎ ‎∴CD=AD，∠CDP=∠ADP，‎ ‎∴△CDP≌△ADP，‎ ‎∴∠DCP=∠DAP；‎ ‎（2）解：∵四边形ABCD为菱形，‎ ‎∴CD∥BA，CD=BA，‎ ‎∴△CPD∽△FPB，‎ ‎∴===，‎ ‎∴CD=BF，CP=PF，‎ ‎∴A为BF的中点，‎ 又∵PA⊥BF，‎ ‎∴PB=PF，‎ 由（1）可知，PA=CP，‎ ‎∴PA=PB，在Rt△PAB中，‎ PB2=22+（PB）2，‎ 解得PB=，‎ 则PD=，‎ ‎∴BD=PB+PD=2．‎ 点评：本题考查了全等三角形、相似三角形的判定与性质，菱形的性质及勾股定理的运用．关键是根据菱形的四边相等，对边平行及菱形的轴对称性解题．‎ 四川省绵阳 ‎24．已知抛物线y = x2－2x + m－1与x轴只有一个交点，且与y轴交于A点，如图，设它的顶点为B．‎ F E C O A B x y ‎（1）求m的值；‎ ‎（2）过A作x轴的平行线，交抛物线于点C，求证：△ABC是等腰直角三角形；‎ ‎（3）将此抛物线向下平移4个单位后，得到抛物线C′，且与x轴的左半轴 交于E点，与y轴交于F点，如图．请在抛物线C′上求点P，使得△EFP是以 EF为直角边的直角三角形．‎ ‎24．（1）∵ 抛物线y = x2－2x + m－1与x轴只有一个交点，∴ △=（－2）2－4×1×（m－1）= 0，解得 m = 2．‎ ‎（2）由（1）知抛物线的解析式为 y = x2－2x + 1，易得顶点B（1，0），当 x = 0时，y = 1，得A（0，1）．‎ 由 1 = x2－2x + 1 解得 x = 0（舍），或 x = 2，所以C（2，1）．‎ 过C作x轴的垂线，垂足为D，则 CD = 1，BD = xD－xB = 1．‎ ‎∴ 在Rt△CDB中，∠CBD = 45°，BC =．‎ 同理，在Rt△AOB中，AO = OB = 1，于是 ∠ABO = 45°，AB =．‎ ‎∴ ∠ABC = 180°－∠CBD－∠ABO = 90°，AB = BC，因此△ABC是等腰直角三角形．‎ ‎（3）由题知，抛物线C′ 的解析式为y = x2－2x －3，当 x = 0时，y =－3；当y = 0时，x =－1，或x = 3，‎ ‎∴ E（－1，0），F（0，－3），即 OE = 1，OF = 3．‎ ‎① 若以E点为直角顶点，设此时满足条件的点为P1（x1，y1），作P‎1M⊥x轴于M．‎ ‎∵ ∠P1EM +∠OEF =∠EFO +∠OEF = 90°，‎ ‎∴ ∠P1EM =∠EFO，得 Rt△EFO∽Rt△P1EM，于是 ，即EM = 3 P‎1M．‎ ‎∵ EM = x1 + 1，P‎1M = y1，∴ x1 + 1 = 3 y1． （*）‎ 由于P1（x1，y1）在抛物线C′ 上，有 3（x12－2x1－3）= x1 + 1，‎ 整理得 3x12－7x1－10 = 0，解得 x1 =－1（舍），或．‎ 把代人（*）中可解得． ∴ P1（，）．‎ ‎② 若以F点为直角顶点，设此时满足条件的点为P2（x2，y2），作P2N⊥与y轴于N．‎ 同①，易知 Rt△EFO∽Rt△FP2N，得 ，即P2N = 3 FN．‎ ‎∵ P2N = x2，FN = 3 + y2，∴ x2 = 3（3 + y2）． （**）‎ 由于P2（x2，y2）在抛物线C′ 上，有 x2 = 3（3 + x22－2x2－3），‎ 整理得 3x22－7x2 = 0，解得 x2 = 0（舍），或．‎ 把代人（**）中可解得． ∴ P2（，）．‎ 综上所述，满足条件的P点的坐标为（，）或（，）．‎ 四川省内江 ‎27、（2011•内江）某电脑经销商计划购进一批电脑机箱和液晶显示器，若购电脑机箱10台和液液晶显示器8台，共需要资金7000元；若购进电脑机箱2台和液示器5台，共需要资金4120元．‎ ‎（1）每台电脑机箱、液晶显示器的进价各是多少元？‎ ‎（2）该经销商购进这两种商品共50台，而可用于购买这两种商品的资金不超过22240元．根据市场行情，销售电脑机箱、液晶显示器一台分别可获利10元和160元．该经销商希望销售完这两种商品，所获利润不少于4100元．试问：该经销商有哪几种进货方案？哪种方案获利最大？最大利润是多少？‎ 考点：一元一次不等式组的应用；二元一次方程组的应用。‎ 分析：（1）根据购电脑机箱10台和液液晶显示器8台，共需要资金7000元；若购进电脑机箱2台和液示器5台，共需要资金4120元，得出等量关系，列出一元二次方程组即可；‎ ‎（2）根据该经销商购进这两种商品共50台，而可用于购买这两种商品的资金不超过22240元．根据市场行情，销售电脑机箱、液晶显示器一台分别可获利10元和160元．该经销商希望销售完这两种商品，所获利润不少于4100元，即可得出不等式组，求出即可．‎ 解答：解：（1）设每台电脑机箱、液晶显示器的进价各是x，y元，‎ 根据题意得：，‎ 解得：，‎ 答：每台电脑机箱、液晶显示器的进价各是60元，800元；‎ ‎（2）设该经销商购进电脑机箱m台，购进液晶显示器（50﹣m）台，‎ 根据题意得：，‎ 解得：24≤m≤26，‎ 因为m要为整数，所以m可以取24、25、26，‎ 从而得出有三种进货方式：①电脑箱：24台，液晶显示器：26台，‎ ‎②电脑箱：25台，液晶显示器：25台；‎ ‎③电脑箱：26台，液晶显示器：24台．‎ ‎∴方案一的利润：24×10+26×160=4400，‎ 方案二的利润：25×10+25×160=4250，‎ 方案三的利润：26×10+24×160=4100，‎ ‎∴方案一的利润最大为4400元．‎ 点评：此题主要考查了二元一次方程组的应用以及不等式组的应用，根据题意得出等量关系是解决问题的关键．‎ 四川省南充 ‎21.如图，等腰梯形ABCD中，AD∥BC,AD=AB=CD=2,∠C=600,M是BC的中点。‎ ‎（1）求证：⊿MDC是等边三角形；‎ ‎（2）将⊿MDC绕点M旋转，当MD(即MD′)与AB交于一点E,MC即MC′)同时与AD交于一点F时，点E,F和点A构成⊿AEF.试探究⊿‎ AEF的周长是否存在最小值。如果不存在，请说明理由；如果存在，请计算出⊿AEF周长的最小值。‎ ‎21.（1）证明：过点D作DP⊥BC,于点P，过点A作AQ⊥BC于点Q,‎ ‎∵∠C=∠B=600 ∴CP=BQ=AB,CP+BQ=AB ……………. （1分）‎ 又∵ADPQ是矩形，AD=PQ,故BC=2AD,‎ 由已知，点M是BC的中点，BM=CM=AD=AB=CD, ……………. （2分）‎ 即⊿MDC中，CM=CD, ∠C=600,故⊿MDC是等边三角形。………. （3分）‎ ‎（2）解：⊿AEF的周长存在最小值，理由如下：‎ 连接AM,由（1）平行四边形ABMD是菱形，⊿MAB, ⊿MAD和⊿MC′D′是等边三角形，‎ ‎∠BMA=∠BME+∠AME=600, ∠EMF=∠AMF+∠AME=600 ∴∠BME=∠AMF…………. （5分）‎ 在⊿BME与⊿AMF中，BM=AM, ∠EBM=∠FAM=600 ∴⊿BME≌⊿AMF(ASA) …. （6分）‎ ‎∴BE=AF, ME=MF,AE+AF=AE+BE=AB ‎∵∠EMF=∠DMC=600 ,故⊿EMF是等边三角形，EF=MF. ……………. （7分）‎ ‎∵MF的最小值为点M到AD的距离，即EF的最小值是。‎ ‎⊿AEF的周长=AE+AF+EF=AB+EF, ⊿AEF的周长的最小值为2+.………. （8分）‎ 四川省攀枝花 ‎23、（2011•攀枝花）如图（Ⅰ），在平面直角坐标系中，⊙O′是以点O′（2，﹣2）为圆心，半径为2的圆，⊙O″是以点O″（0，4）为圆心，半径为2的圆．‎ ‎（1）将⊙O′竖直向上平移2个单位，得到⊙O1，将⊙O″水平向左平移1个单位，得到⊙O2如图（Ⅱ），分别求出⊙O1和⊙O2的圆心坐标．‎ ‎（2）两圆平移后，⊙O2与y轴交于A、B两点，过A、B两点分别作⊙O2的切线，交x轴与C、D两点，求△O‎2AC和△O2BD的面积．‎ 考点：切线的性质；坐标与图形变化-平移。‎ 专题：综合题。‎ 分析：（1）根据“左减右加，下减上加”的规律对点O′，O″的坐标进行平移即可得到点O1，O2的坐标；‎ ‎（2）先求出点A、B的坐标，然后连接O‎2A，O2B，根据直角三角形30度角所对的直角边等于斜边的一半得出∠O2AB=∠O2BA=30°，又AC与BD是圆的切线，然后求出∠OAC=∠OBD=60°，利用特殊角的三角函数与点A，B的坐标即可求出AC、BD的长，最后代入三角形的面积公式进行计算即可．‎ 解答：解：（1）∵﹣2+2=0，‎ ‎∴点O1的坐标为：（2，0），‎ ‎∵0﹣1=﹣1，‎ ‎∴点O2的坐标为：（﹣1，4）；‎ ‎（2）如图，连接O‎2A，O2B，∵⊙O2的半径为2，圆心O2到y轴的距离是1，‎ ‎∴∠O2AB=∠O2BA=30°，‎ ‎∴AB=2×2cos30°=2，‎ ‎∴点A、B的坐标分别为A（0，4﹣），B（0，4+），‎ ‎∵AC，BD都是⊙O2的切线，‎ ‎∴∠OAC=180°﹣90°﹣30°=60°，‎ ‎∠OBD=90°﹣30°=60°，‎ ‎∴AC=（4﹣）÷cos60°=8﹣2，‎ BD=（4+）÷cos60°=8+2，‎ ‎∴S△O‎2AC=×AC×O‎2A=×（8﹣2）×2=8﹣2，‎ S△O2BD=×BD×O2B=×（8+2）×2=8+2．‎ 故答案为：8﹣2，8+2．‎ 点评：本题主要考查了切线的性质与坐标的平移，利用数据的特点求出30度角是解题的关键，也是解答本题的难点与突破口，本题难度适中，有一定的综合性．‎ 四川省雅安 ‎24、（2011•雅安）如图，在△ABC中，AB=AC，以AB为直径作⊙O，交BC于点D，过点D作DE⊥AC，垂足为E．‎ ‎（1）求证：DE是⊙O的切线；‎ ‎（2）如果BC=8，AB=5，求CE的长．‎ 考点：切线的判定与性质；勾股定理；圆周角定理；相似三角形的判定与性质。‎ 专题：证明题。‎ 分析：（1）连接OD，只要证明OD⊥DE即可；‎ ‎（2）连接AD构造直角三角形ACD，根据相似三角形的判定定理AA判定Rt△ACD∽Rt△DCE，然后由相似三角形的对应边成比例得，=；最后根据三角形中位线的判定与性质求得CD的长度，从而求得CE的长．‎ 解答：解：（1）证明：连接OD．‎ ‎∵OD=OB？（⊙O的半径），‎ ‎∴∠B=∠ODB（等边对等角）；‎ ‎∵AB=AC（已知），‎ ‎∴∠B=∠C（等边对等角）；‎ ‎∴∠C=∠ODB（等量代换），‎ ‎∴OD∥AC（同位角相等，两直线平行），‎ ‎∴∠ODE=∠DEC（两直线平行，内错角相等）；‎ ‎∵DE⊥AC（已知），‎ ‎∴∠DEC=90°，‎ ‎∴∠ODE=90°，即DE⊥OD，‎ ‎∴DE是⊙O的切线；‎ ‎（2）连接AD．‎ ‎∵AB是⊙O的直径，‎ ‎∴∠ADB=90°（直径所对的圆周角是直角）；‎ ‎∴AD⊥CD；‎ 在Rt△ACD和Rt△DCE中，‎ ‎∠C=∠C（公共角），‎ ‎∠CED=∠CDA=90°，‎ ‎∴Rt△ACD∽Rt△DCE（AA），‎ ‎∴=；‎ 又由（1）知，OD∥AC，O是AB的中点，‎ ‎∴OD是三角形ABC的中位线，‎ ‎∴CD=BC；‎ ‎∵BC=8，AB=5，AB=AC，‎ ‎∴CE=．‎ 点评：本题综合考查了切线的判定与性质、圆周角定理、相似三角形的判定与性质以及三角形中位线的判定与性质．解答（2）时，还可以利用射影定理来求CE的长度．‎ 四川省宜宾 ‎23．已知：在△ABC中，以AC边为直径的⊙O交BC于点D，在劣弧上取一点E使∠EBC = ∠DEC，延长BE依次交AC于G，交⊙O于H.‎ ‎(1)求证：AC⊥BH ‎ (2)若∠ABC= 45°，⊙O的直径等于10，BD =8，求CE的长.‎ ‎(23题图)‎ ‎23．证明：（1）连结AD (1分)‎ ‎ ∵∠DAC = ∠DEC ∠EBC = ∠DEC ‎ ∴∠DAC = ∠EBC (2分)‎ ‎ 又∵AC是⊙O的直径 ∴∠ADC=90° (3分)‎ ‎ ∴∠DCA+∠DAC=90° ∴∠EBC+∠DCA = 90°‎ ‎ ∴∠BGC=180°–（∠EBC+∠DCA) = 180°–90°=90°‎ ‎ ∴AC⊥BH （5分）‎ ‎ （2）∵∠BDA=180°–∠ADC = 90° ∠ABC = 45° ∴∠BAD = 45°‎ ‎ ∴BD = AD ‎ ∵BD = 8 ∴AD =8 （6分）‎ ‎ 又∵∠ADC = 90° AC =10 ‎ ‎ ∴由勾股定理 DC== = 6‎ ‎ ∴BC=BD+DC=8+6=14 (7分)‎ ‎ 又∵∠BGC = ∠ADC = 90° ∠BCG =∠ACD ‎ ∴△BCG∽△ACD ‎ ∴ = ‎ ∴ = ∴CG = (8分)‎ ‎ 连结AE ∵AC是直径 ∴∠AEC=90° 又因 EG⊥AC ‎ ∴ △CEG∽△CAE ∴ = ∴CE2=AC · CG = ´ 10 = 84‎ ‎ ∴CE = = 2 （10分）‎ ‎(23题图)‎ 天津市 ‎ (25) (本小题10分) 在平面直角坐标系中．已知O坐标原点．点A(3．0)，B(0，4)．以点A为旋转中心，把△ABO顺时针旋转，得△ACD．记旋转转角为α．∠ABO为β．‎ ‎ (I) 如图①，当旋转后点D恰好落在AB边上时．求点D的坐标；‎ ‎ (Ⅱ) 如图②，当旋转后满足BC∥x轴时．求α与β之闻的数量关系；‎ ‎(Ⅲ) 当旋转后满足∠AOD=β时．求直线CD的解析式(直接写出即如果即可)，‎ ‎（25）（本小题10分）‎ 解：(I)∵点A(3，0)．B(0，4)．得‎0A=3，OB=4．‎ ‎ ∴在Rt△ABO中．由勾股定理．得AB=5，‎ ‎ 根据题意，有DA=OA=3‎ 如图①．过点D作DM⊥x轴于点M，则MD∥OB．‎ ‎∴△ADM∽△ABO。有，‎ 得 ‎ 又OM=OA-AM，得OM=．∴点D的坐标为（）‎ ‎(Ⅱ)如图②．由己知，得∠CAB=α，AC=AB，∴∠ABC=∠ACB．‎ ‎∴在△ABC中，由∠ABC+∠ACB+∠CAB=180°，得α=180°—2∠ABC，．‎ 又∵BC∥x轴，得∠OBC=90°，‎ 有∠ABC=90°—∠ABO=90°—β ∴α=2β．‎ ‎（Ⅲ） 直线CD的解析式为，或．‎ 新疆乌鲁木齐 ‎23.小王从A地前往B地，到达后立刻返回，他与A地的距离y（千米）和所用的时间x（小时）之间的函数关系如图所示。‎ ‎（1）小王从B地返回A地用了多少小时？‎ ‎（2）求小王出发6小时后距A地多远？‎ ‎（3）在A、B之间友谊C地，小王从去时途经C地，到返回时路过C地，共用了2小时20分，求A、C两地相距多远？‎ ‎23. 解：（1）小王从B地返回A地用了4小时。‎ ‎（2）小王出发6小时，∵6>3，可知小王此时在返回途中。‎ 于是，设DE所在直线的解析式为，由图象可得：‎ ‎，解得 ‎∴DE所在直线的解析式为 当x=6时，有 ‎∴小王出发6小时后距A地‎60千米。‎ ‎（3）设AD所在直线的解析式为，易求 ‎∴AD所在直线的解析式为 设小王从C到B用了小时，则去时C距A的距离为 返回时，从B到C用了（）小时，‎ 这时C距A的距离为 由，解得 故C距A的距离为米 云南省大理州保山 ‎23、（2011•保山）随着人们节能环保意识的增强，绿色交通工具越来越受到人们的青睐，电动摩托成为人们首选的交通工具，某商场计划用不超过140000元购进A、B两种不同品牌的电动摩托40辆，预计这批电动摩托全部销售后可获得不少于29000元的利润，A、B两种品牌电动摩托的进价和售价如下表所示：‎ 品牌 价格 A品牌电动摩托 B品牌电动摩托 进价（元/辆）‎ ‎4000‎ ‎3000‎ 售价（元/辆）‎ ‎5000‎ ‎3500‎ 设该商场计划进A品牌电动摩托x辆，两种品牌电动摩托全部销售后可获利润y元．‎ ‎（1）写出y与x之间的函数关系式；‎ ‎（2）该商场购进A品牌电动摩托多少辆时？获利最大，最大利润是多少？‎ 考点：一次函数的应用。‎ 专题：应用题。‎ 分析：（1）根据题中已知条件列出关于x的一次函数即可；‎ ‎（2）根据题意列出不等式，解不等式便可求出x的取值范围，可知当x=20时，所获得的利润最大．‎ 解答：解：（1）设该商场计划进A品牌电动摩托x辆，则进B品牌电动摩托（40﹣x）辆，由题意可知每辆A品牌电动摩托的利润为1000元，每辆B品牌电动摩托的利润为500元，则y=1000x+500（40﹣x）=20000+500x，‎ ‎（2）由题意可知；‎ 解得18≤x≤20；当x=20时，y=30000‎ ‎∴该商场购进A品牌电动摩托20辆时，获利最大，最大利润是30000．‎ 点评：本题主要考查了一次函数的实际应用，分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键，属于中档题．‎ 云南省昆明 ‎24、如图，已知AB是⊙O的直径，点E在⊙O上，过点E的直线EF与AB的延长线交与点F，AC⊥EF，垂足为C，AE平分∠FAC．‎ ‎（1）求证：CF是⊙O的切线；‎ ‎（2）∠F=30°时，求的值？‎ 答案：（1）证明：连接OE，∵AE平分∠FAC，∴∠CAE=∠OAE，‎ 又∵OA=OE，∠OEA=∠OAE，∠CAE=∠OEA，∴OE∥AC，‎ ‎∴∠OEF=∠ACF，又∵AC⊥EF，∴∠OEF=∠ACF=90°，‎ ‎∴OE⊥CF，又∵点E在⊙O上，∴CF是⊙O的切线；‎ ‎（2）∵∠OEF=90°，∠F=30°，∴OF=2OE 又OA=OE，∴AF=3OE，又∵OE∥AC，∴△OFE∽△AFC，‎ ‎∴，∴，∴．‎ 云南省曲靖 ‎23、（2011•曲靖）如图，点A、B、C、D都在⊙O上，OC⊥AB，∠ADC=30°．‎ ‎（1）求∠BOC的度数；‎ ‎（2）求证：四边形AOBC是菱形．‎ 考点：圆周角定理；菱形的判定；垂径定理。‎ 分析：（1）根据垂径定理得出=，再利用圆周角定理得出∠BOC的度数；‎ ‎（2）根据等边三角形的判定得出BC=BO=CO，进而利用（1）中结论得出AO=BO=AC=BC，即可证明结论．‎ 解答：解：（1）∵点A、B、C、D都在⊙O上，OC⊥AB，‎ ‎∴=，‎ ‎∵∠ADC=30°，‎ ‎∴∠AOC=∠BOC=2∠ADC=60°，‎ ‎∴∠BOC的度数为60°；‎ ‎（2）证明：∵=，‎ ‎∴AC=BC，‎ AO=BO，‎ ‎∵∠BOC的度数为60°，‎ ‎∴△BOC为等边三角形，‎ ‎∴BC=BO=CO，‎ ‎∴AO=BO=AC=BC，‎ ‎∴四边形AOBC是菱形．‎ 点评：此题主要考查了菱形的判定以及垂径定理和圆周角定理等知识，根据垂径定理得出=是解决问题的关键．‎ 浙江省杭州 ‎23. （本小题满分10分）[来源设函数（为实数）‎ ‎（1）写出其中的两个特殊函数，使它们的图像不全是抛物线，并在同一直角坐标系中，用描点法画出这两个特殊函数的图像；‎ ‎（2）根据所画图像，猜想出：对任意实数，函数的图像都具有的特征，并给予证明；‎ ‎（3）对任意负实数，当时，随着的增大而增大，试求出的一个值 ‎23、解：（1）如两个函数为，函数图形略；‎ ‎　　　　（2）不论k取何值，函数的图象必过定点，‎ 且与轴至少有1个交点.证明如下：‎ 由，得 当即时，上式对任意实数k都成立，所以函数的图像必过定点.‎ 又因为当时，函数的图像与x轴有一个交点；‎ 当时，，所以函数图像与x轴有两个交点.‎ 所以函数的图象与轴至少有1个交点.‎ ‎　　　　（3）只要写出的数都可以.‎ ‎，函数的图像在对称轴直线 ‎　　　　　　的左侧，随的增大而增大.‎ ‎　　　　　　根据题意，得，而当时，‎ ‎　　　　　　所以.‎ 浙江省湖州 ‎23、（2011•湖州）我市水产养殖专业户王大爷承包了30亩水塘，分别养殖甲鱼和桂鱼，有关成本、销售情况如下表：‎ 养殖种类 成本（万元）‎ 销售额（万元/亩）‎ 甲鱼 ‎2.4‎ ‎3‎ 桂鱼 ‎2‎ ‎2.5‎ ‎（1）2010年，王大爷养殖甲鱼20亩，桂鱼10亩，求王大爷这一年共收益多少万元？（收益=销售额﹣成本）‎ ‎（2）2011年，王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼，计划投入成本不超过70万元．若每亩养殖的成本、销售额与2010年相同，要获得最大收益，他应养殖甲鱼和桂鱼各多少亩？‎ ‎（3）已知甲鱼每亩需要饲料500㎏，桂鱼每亩需要饲料700㎏，根据（2）中的养殖亩数，为了节约运输成本，实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍，结果运输养殖所需要全部饲料比原计划减少了2次，求王大爷原定的运输车辆每次可装载饲料多少㎏？‎ 考点：一次函数的应用；分式方程的应用；一元一次不等式的应用。‎ 专题：函数思想；方程思想。‎ 分析：（1）根据已知列算式求解；‎ ‎（2）先设养殖甲鱼x亩，则养殖桂鱼（30﹣x）亩列不等式，求出x的取值，再表示出王大爷可获得收益为y万元函数关系式求最大值；‎ ‎（3）设大爷原定的运输车辆每次可装载饲料a㎏，结合（2）列分式方程求解．‎ 解答：解：（1）2010年王大爷的收益为：‎ ‎20×（3﹣2.4）+10×（2.5﹣2）=17（万元），‎ 答：王大爷这一年共收益17万元．‎ ‎（2）设养殖甲鱼x亩，则养殖桂鱼（30﹣x）亩 则题意得2.4x+2（30﹣x）≤70 解得x≤25，‎ 又设王大爷可获得收益为y万元，‎ 则y=0.6x+0.5（30﹣x），即y=x+15．‎ ‎∵函数值y随x的增大而增大，∴当x=25时，可获得最大收益．‎ 答：要获得最大收益，应养殖甲鱼25亩，桂鱼5亩．‎ ‎（3）设大爷原定的运输车辆每次可装载饲料a㎏ 由（2）得，共需要饲料为500×25+700×5=16000㎏，根据题意得﹣=2，解得a=4000㎏．‎ 答：王大爷原定的运输车辆每次可装载饲料4000㎏．‎ 点评：此题考查的知识点是一次函数的应用，分是方程的应用及一元一次不等式的应用，解题的关键是列不等式求x的取值范围，再表示出函数关系求最大值，再列分式方程求解．‎ 浙江省嘉兴 ‎23、（2011•舟山）以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连接这四个点，得四边形EFGH．‎ ‎（1）如图1，当四边形ABCD为正方形时，我们发现四边形EFGH是正方形；如图2，当四边形ABCD为矩形时，请判断：四边形EFGH的形状（不要求证明）；‎ ‎（2）如图3，当四边形ABCD为一般平行四边形时，设∠ADC=α（0°＜α＜90°），‎ ‎①试用含α的代数式表示∠HAE；‎ ‎②求证：HE=HG；‎ ‎③四边形EFGH是什么四边形？并说明理由．‎ 考点：正方形的判定；全等三角形的判定与性质；等腰直角三角形；菱形的判定与性质。‎ 专题：证明题。‎ 分析：（1）根据等腰直角三角形得到角都是直角，且边都相等即可判断答案；‎ ‎（2）①∠HAE=90°+a，根据平行四边形的性质得出，∠BAD=180°﹣a，根据△HAD和△EAB是等腰直角三角形，得到∠HAD=∠EAB=45°，求出∠HAE即可；‎ ‎②根据△AEB和△DGC是等腰直角三角形，得出AE=AB，DC=CD，平行四边形的性质得出AB=CD，求出∠HDG=90°+a=∠HAE，证△HAE≌△HDC，即可得出HE=HG；‎ ‎③由②同理可得：GH=GF，FG=FE，推出GH=GF=EF=HE，得出菱形EFGH，证△HAE≌△HDG，求出∠AHD=90°，∠EHG=90°，即可推出结论．‎ 解答：（1）答：四边形EFGH的形状是正方形．‎ ‎（2）解：①∠HAE=90°+a，‎ 在平行四边形ABCD中AB∥CD，∴∠BAD=180°﹣∠ADC=180°﹣a，‎ ‎∵△HAD和△EAB是等腰直角三角形，∴∠HAD=∠EAB=45°，‎ ‎∴∠HAE=360°﹣∠HAD﹣∠EAB﹣∠BAD=360°﹣45°﹣45°﹣（180°﹣a）=90°+a，‎ 答：用含α的代数式表示∠HAE是90°+a．‎ ‎②证明：∵△AEB和△DGC是等腰直角三角形，‎ ‎∴AE=AB，DC=CD，‎ 在平行四边形ABCD中，AB=CD，∴AE=DG，‎ ‎∵△HAD和△GDC是等腰直角三角形，∴∠HDA=∠CDG=45°，‎ ‎∴∠HDG=∠HDA+∠ADC+∠CDG=90°+a=∠HAE，‎ ‎∵△HAD是等腰直角三角形，∴HA=HD，∴△HAE≌△HDC，∴HE=HG．‎ ‎③答：四边形EFGH是正方形，‎ 理由是：由②同理可得：GH=GF，FG=FE，‎ ‎∵HE=HG，∴GH=GF=EF=HE，∴四边形EFGH是菱形，‎ ‎∵△HAE≌△HDG，∴∠DHG=∠AHE，‎ ‎∵∠AHD=∠AHG+∠DHG=90°，∴∠EHG=∠AHG+∠AHE=90°，∴四边形EFGH是正方形．‎ 点评：本题主要考查对正方形的判定，等腰直角三角形的性质，菱形的判定和性质，全等三角形的性质和判定，平行线的性质等知识点的理解和掌握，综合运用性质进行推理是解此题的关键．‎ 浙江省金华丽水 在平面直角坐标系中，如图1，将个边长为1的正方形并排组成矩形OABC, 相邻两边OA和OC分别落在轴和轴的正半轴上, 设抛物线（＜0）过矩形顶点B、C.‎ ‎（1）当n=1时，如果=-1，试求b的值；‎ ‎（2）当n=2时，如图2，在矩形OABC上方作一边长为1的正方形EFMN，使EF在线段CB上，如果M，N两点也在抛物线上，求出此时抛物线的解析式；‎ ‎（3）将矩形OABC绕点O顺时针旋转，使得点B落到轴的正半轴上，如果该抛物线同时经过原点O.‎ ‎①试求当n=3时a的值；②直接写出关于的关系式．‎ y x O C A B ‎（1）由题意可知，抛物线对称轴为直线x=，‎ ‎∴,得b= 1； ……2分 ‎（2）设所求抛物线解析式为，‎ x y O C E A B M N F 由对称性可知抛物线经过点B（2，1）和点M（，2）‎ ‎∴ 解得 ‎ ‎∴所求抛物线解析式为；……4分 ‎（3）①当n=3时，OC=1，BC=3，‎ x y O A B C D 设所求抛物线解析式为，‎ 过C作CD⊥OB于点D，则Rt△OCD∽Rt△CBD，‎ ‎∴, ‎ 设OD=t，则CD=3t，∵， ‎ ‎∴， ∴,‎ ‎∴C（，）, 又 B（，0）， ‎ ‎∴把B 、C坐标代入抛物线解析式，得 ‎ 解得:a=； ……2分 ‎②. ……2分 浙江省宁波 ‎25．（本题10分）阅读下面的情景对话，然后解答问题：‎ ‎（1）根据“奇异三角形”的定义，请你判断小华提出的命题：“等边三角形一定是奇异三角形”是真命题还是假命题？‎ 小明：那直角三角形中是否存在奇异三角形呢？‎ ‎（2）在Rt△ABC中，∠ACB＝90°，AB=，AC=，BC=，且，若Rt△ABC是奇异三角形，求； ‎ 老师：我们新定义一种三角形，两边平方和等于第三边平方的2倍的三角形叫做奇异三角形．‎ 小华：等边三角形一定是奇异三角形！‎ ‎（3）如图，AB是⊙O的直径，C是⊙O上一点(不与点A、B重合)，‎ D是半圆ADB的中点， C、D在直径AB两侧，若在⊙O内存在点E，‎ ‎(第25题)‎ A B C D E O 使得AE=AD，CB=CE．‎ ① 求证：△ACE是奇异三角形；‎ ② 当△ACE是直角三角形时，求∠AOC的度数．‎ ‎25．解：(1) 真命题 ‎ ‎(2) 在Rt△ABC中， ‎ ‎ ∵ ∴，‎ ‎∴若Rt△ABC为奇异三角形,一定有 ‎ ‎∴ ∴ 得 ‎∵ ∴ ∴ ‎ ‎(3) ①∵AB是⊙O的直径 ∴∠ACB=∠ADB=90°‎ 在Rt△ACB中， ‎ 在Rt△ADB中，‎ ‎∵点D是半圆ADB的中点 ∴AD= BD ∴AD=BD ‎ ‎∴ ∴ ‎ 又∵∴∴△是奇异三角形 ‎ ②由①可得△是奇异三角形∴‎ 当△是直角三角形时 由（2）可得或 　 ‎ ‎（Ⅰ）当时， ‎ ‎ 即 ‎ ‎∵∴∴ ‎ ‎（Ⅱ）当时，‎ ‎ 即 ‎∵∴∴∴的度数为． ‎ 浙江省衢州市 ‎23、(本题10分)‎ ‎△ABC是一张等腰直角三角形纸板，∠C=Rt∠，AC=BC=2，(1)要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法(如图1)，比较甲、乙两种剪法，哪种剪法所得的正方形面积大？请说明理由。(2)图1中甲种剪法称为第1次剪取，记所得正方形面积为；按照甲种剪法，在余下的△ADE和△BDF中，分别剪取正方形，得到两个相同的正方形，称为第2次剪取，并记这两个正方形面积和为(如图2)，则；再在余下的四个三角形中，用同样方法分别剪取正方形，得到四个相同的正方形，称为第3次剪取，并记这四个正方形面积和为，继续操作下去……，则第10次剪取时，；‎ ‎(3)求第10次剪取后，余下的所有小三角形的面积之和。‎ ‎23、(1)解法1：如图甲，由题意，得AE=DE=EC，即EC=1，‎ ‎ 如图乙，设MN=x，则由题意，得AM=MQ=PN=NB=MN=x，‎ ‎ ∴，解得 ∴‎ ‎ 又∵ ∴甲种剪法所得的正方形面积更大。‎ ‎ 说明：图甲可另解为：由题意得点D、E、F分别为AB、AC、BC的中点，‎ ‎ 解法2：如图甲，由题意得AE=DE=EC，即EC=1‎ ‎ 如图乙，设MN=x，则由题意得AM=MQ=QP=PN=NB=MN=x，‎ ‎ ∴，解得 ‎ 又∵，即 ∴甲种剪法所得的正方形面积更大。‎ ‎(2) ‎ ‎(3)解法1：探索规律可知：‎ ‎ 剩余三角形面积和为 ‎ ‎ 解法2：由题意可知，‎ ‎ 第一次剪取后剩余三角形面积和为 ‎ 第二次剪取后剩余三角形面积和为 ‎ 第三次剪取后剩余三角形面积和为 ‎ ……‎ ‎ 第十次剪取后剩余三角形面积和为 浙江省绍兴 ‎23、（2011•绍兴）数学课上，李老师出示了如下框中的题目．‎ 在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED=EC，如图．试确定线段AE与DB的大小关系，并说明理由．‎ 小敏与同桌小聪讨论后，进行了如下解答：‎ ‎（1）特殊情况•探索结论 当点E为AB的中点时，如图1，确定线段AE与的DB大小关系．请你直接写出结论：AE　=　DB（填“＞”，“＜”或“=”）．‎ ‎（2）特例启发，解答題目 解：题目中，AE与DB的大小关系是：AE　=　DB（填“＞”，“＜”或“=”）．理由如下：‎ 如图2，过点E作EF∥BC，交AC于点F，（请你完成以下解答过程）‎ ‎（3）拓展结论，设计新题 在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC．若△ABC的边长为1，AE=2，求CD的长（请你直接写出结果）．‎ 考点：全等三角形的判定与性质；三角形内角和定理；等边三角形的判定与性质。‎ 专题：计算题；证明题；分类讨论。‎ 分析：（1）根据等边三角形的性质和三角形的内角和定理求出∠D=∠DEB=30°，推出DB=BE=AE即可得到答案；‎ ‎（2）作EF∥BC，证出等边三角形AEF，再证△DBE≌△EFC即可得到答案；‎ ‎（3）分为两种情况：一是如上图在AB边上，在CB的延长线上，求出CD=3，二是在BC上求出CD=1，即可得到答案．‎ 解：（1）故答案为：=．（2）故答案为：=．‎ 证明：在等边△ABC中，∠ABC=∠ACB=∠BAC=60°，AB=BC=AC，‎ ‎∵EF∥BC，‎ ‎∴∠AEF=∠AFE=60°=∠BAC，∴AE=AF=EF，‎ ‎∴AB﹣AE=AC﹣AF，即BE=CF，‎ ‎∵∠ABC=∠EDB+∠BED=60°，∠ACB=∠ECB+∠FCE=60°，‎ ‎∵ED=EC，∴∠EDB=∠ECB，∴∠BED=∠FCE，‎ ‎∴△DBE≌△EFC，∴DB=EF，∴AE=BD．‎ ‎（3）答：CD的长是1或3．‎ 点评：本题主要考查对全等三角形的性质和判定，三角形的内角和定理，等边三角形的性质和判定等知识点的理解和掌握，能综合运用这些性质进行推理是解此题的关键．‎ 浙江省台州 ‎23、（2011•台州）如图1，AD和AE分别是△ABC的BC边上的高和中线，点D是垂足，点E是BC的中点，规定：λA=．特别地，当点D、E重合时，规定：λA=0．另外，对λB、λC作类似的规定．‎ ‎（1）如图2，在△ABC中，∠C=90°，∠A=30°，求λA、λC；‎ ‎（2）在每个小正方形边长均为1的4×4的方格纸上，画一个△ABC，使其顶点在格点（格点即每个小正方形的顶点）上，且λA=2，面积也为2；‎ ‎（3）判断下列三个命题的真假（真命题打“√”，假命题打“×”）：‎ ‎①若△ABC中λA＜1，则△ABC为锐角三角形；　×　‎ ‎②若△ABC中λA=1，则△ABC为锐角三角形；　√　‎ ‎③若△ABC中λA＞1，则△ABC为钝角三角形．　√　．‎ 考点：解直角三角形；三角形的角平分线、中线和高；作图—应用与设计作图。‎ 专题：应用题。‎ 分析：（1）根据直角三角形斜边中线、高的特点进行转换即可得出答案，‎ ‎（2）根据题目要求即可画出图象，‎ ‎（3）根据真假命题的定义即可得出答案．‎ 解答：解：（1）如图，作BC边上的中线AD，又AC⊥DC，∴λA==1，‎ 过点C分别作AB边上的高CE和中线CF，‎ ‎∵∠ACB=90°，∴AF=CF，∴∠ACF﹣∠CAF=30°，∴∠CFE=60°，∴λC===cos60°=，‎ ‎（2）如图：‎ ‎（3）①×，②√，③√．‎ 点评：本题主要考查了直角三角形斜边中线、高的性质以及特殊角的三角函数值，同时考查了画图，真假命题的判断，比较复杂，难度较大．‎ 浙江省温州 ‎23、（2011•温州）‎2011年5月20日是第22个中国学生营养日，某校社会实践小组在这天开展活动，调查快餐营养情况．他们从食品安全监督部门获取了一份快餐的信息（如图）．根据信息，解答下列问题．‎ ‎（1）求这份快餐中所含脂肪质量；‎ ‎（2）若碳水化合物占快餐总质量的40%，求这份快餐所含蛋白质的质量；‎ ‎（3）若这份快餐中蛋白质和碳水化合物所占百分比的和不高于85%，求其中所含碳水化合物质量的最大值．‎ 考点：一元一次不等式的应用；一元一次方程的应用。‎ 专题：应用题。‎ 分析：（1）快餐中所含脂肪质量=快餐总质量×脂肪所占百分比；‎ ‎（2）根据这份快餐总质量为‎400克，列出方程求解即可；‎ ‎（3）根据这份快餐中蛋白质和碳水化合物所占百分比的和不高于85%，列出不等式求解即可．‎ 解答：解：（1）400×5%=‎20克．‎ 答：这份快餐中所含脂肪质量为‎20克；‎ ‎（2）设所含矿物质的质量为x克，由题意得：x+4x+20+400×40%=400，‎ ‎∴x=44，∴4x=176．‎ 答：所含矿物质的质量为‎176克；‎ ‎（3）设所含矿物质的质量为y克，则所含碳水化合物的质量为（380﹣5y）克．‎ ‎∴4y+（380﹣5y）≤400×85%，∴y≥40，∴380﹣5y≤180，‎ ‎∴所含碳水化合物质量的最大值为‎180克．‎ 点评：本题由课本例题改编而成（原题为浙教版七年级下P96例题），这使学生对试题有“亲切感”，而且对教学有着积极的导向作用．题中第（3）问是本题的一个亮点，给出两个量的和的范围，求其中一个量的最值，隐含着函数最值思想．本题切入点较多，方法灵活，解题方式多样化，可用不等式解题，也可用极端原理求解，不同的解答反映出思维的不同层次．‎ 浙江省义乌 ‎ ‎23．如图1，在等边△ABC中，点D是边AC的中点，点P是线段DC上的动点(点P与点C不重合)，连结BP. 将△ABP绕点P按顺时针方向旋转α角（0°＜α＜180°），得到△A1B1P,连结AA1，射线AA1分别交射线PB、射线B1B于点E、F.‎ ‎ （1） 如图1，当0°＜α＜60°时，在α角变化过程中，△BEF与△AEP始终存在 ▲ 关系（填“相似”或“全等”），并说明理由；‎ ‎（2）如图2，设∠ABP=β . 当60°＜α＜180°时，在α角变化过程中，是否存在△BEF与△AEP全等？若存在，求出α与β之间的数量关系；若不存在，请说明理由； ‎ ‎（3）如图3，当α=60°时，点E、F与点B重合. 已知AB=4，设DP=x，△A1BB1的面 积为S，求S关于x的函数关系式. ‎ 图1‎ 图2‎ 图3‎ P B1‎ FM A DO EC C B A1‎ P B1‎ FM A DO EC C B A1‎ P B1‎ A DO C B A1‎ ‎23．解: （1） 相似 …………………………………………………1分 由题意得：∠APA1=∠BPB1=α AP= A1P BP=B1P ‎ 则 ∠PAA1 =∠PBB1 = ……………………2分 ‎ ∵∠PBB1 =∠EBF ∴∠PAE=∠EBF ‎ 又∵∠BEF=∠AEP ‎ ‎∴△BEF ∽△AEP……………………………………3分 ‎（2）存在，理由如下： ………………………………………4分 易得：△BEF ∽△AEP 若要使得△BEF≌△AEP，只需要满足BE=AE即可……………5分 ‎∴∠BAE=∠ABE P B1‎ A DO C B A1‎ H G ‎ ∵∠BAC=60° ∴∠BAE=‎ ‎∵∠ABE=β ∠BAE=∠ABE ………………………6分 ‎∴ 即α=2β+60° ……………………7分 ‎（3）连结BD，交A1B1于点G，‎ 过点A1作A1H⊥AC于点H. ‎ ‎∵∠B‎1 A1P=∠A1PA=60° ∴A1B1∥AC ‎ 由题意得：AP= A1 P ∠A=60°‎ ‎ ∴△PAA1是等边三角形 ‎∴A1H= ……………………………8分 在Rt△ABD中，BD=‎ ‎ ∴BG=………………… 9分 ‎∴ （0≤x＜2）………10分