中考数学综合练习 9页

‎ 中考数学综合练习（1）‎ 一、选择题：‎ ‎1．计算的结果是（ ）‎ A． B． C． D．‎ ‎2．如果是方程的根，那么的值是（ ）‎ A．0 B．2 C． D．‎ ‎3．在平面直角坐标系中，直线经过（ ）‎ A．第一、二、三象限 B．第一、二、四象限 C．第一、三、四象限 D．第二、三、四象限 ‎4．计算,,则等于（ ）‎ A． B． C． D．‎ ‎5．从一副未曾启封的扑克牌中取出2张红桃，2张黑桃的牌共4张，洗匀后，从这4张牌中任取2张牌恰好是黑桃的概率是（ ）‎ A． B． C． D．‎ ‎6．如图1，在平行四边形中，如果，，那么等于（ ）‎ D C B A 图1‎ A． B． C． D．‎ ‎1‎ A a b B ‎2‎ O ‎1‎ ‎2‎ ‎3‎ ‎4‎ A x y 图2‎ ‎1‎ ‎2‎ C 图3‎ 二、填空题：‎ ‎7．不等式的解集是 ．‎ ‎8．分解因式： ．‎ ‎9．用换元法解分式方程时，如果设，并将原方程化为关于的整式方程，那么这个整式方程是 ．‎ E C D A F B 图4‎ ‎10．方程的根是 ．‎ ‎11．已知函数，那么 ．‎ ‎12．与单位向量方向相反且长度为3的向量为 ．‎ ‎13．在图2中，将直线向右平移1个单位，得到一个一次函数的图像，那么这个一次函数的解析式是 ．‎ ‎14．为了了解某所初级中学学生对“限塑令”是否知道，从该校全体学生1200名中，随机抽查了80名学生，结果显示有2名学生“不知道”．由此，估计该校全体学生中对“限塑令”约有 名学生“不知道”．‎ ‎15．如图3，已知，，，那么的度数等于 ．‎ ‎16．如果两个相似三角形面积的比是，那么这两个三角形的周长比是 ．‎ ‎17．如图4，平行四边形中，是边上的点，交于点，如果，那么 ．‎ ‎18．将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“面线”，“面线”被这个平面图形截得的线段叫做该图形的“面径”，例如圆的直径就是它的“面径”．已知等边三角形的边长为2，则它的“面径”长可以是 .‎ 三、解答题:‎ ‎19．计算：①． ②‎ ‎20.解方程：① ②‎ ‎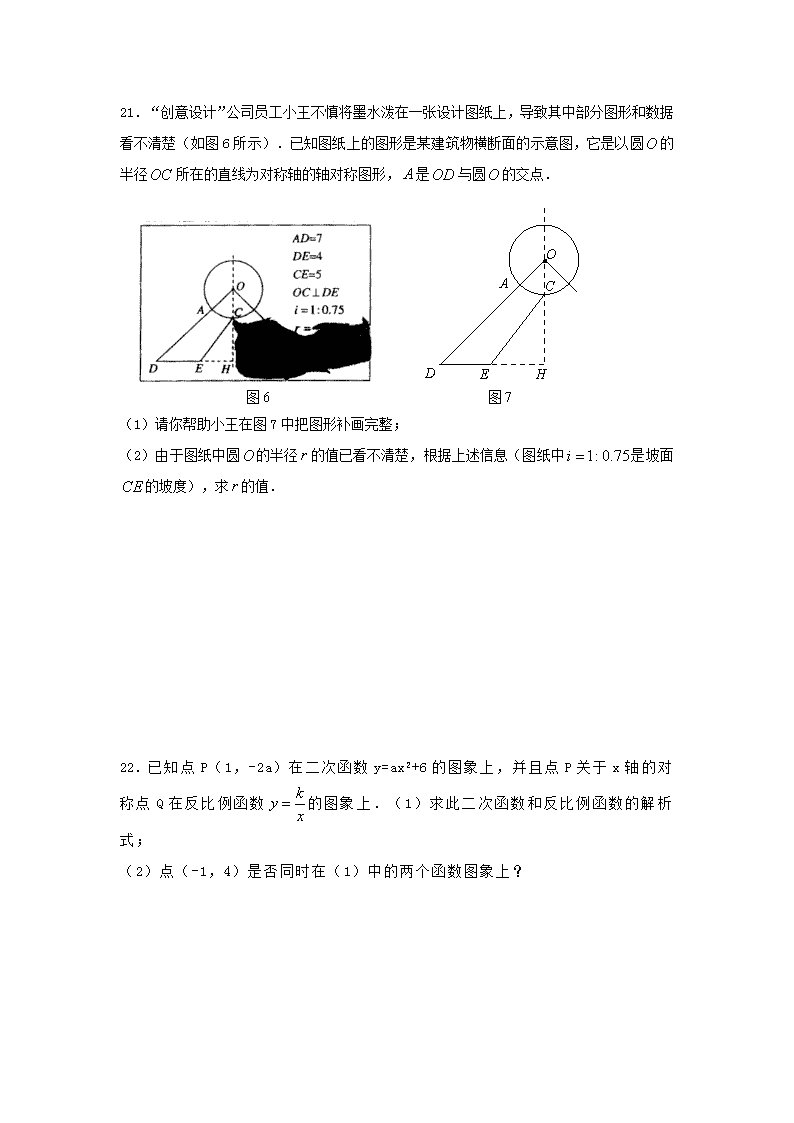21．“创意设计”公司员工小王不慎将墨水泼在一张设计图纸上，导致其中部分图形和数据看不清楚（如图6所示）．已知图纸上的图形是某建筑物横断面的示意图，它是以圆的半径所在的直线为对称轴的轴对称图形，是与圆的交点．‎ O C A D E H 图7‎ 图6‎ ‎（1）请你帮助小王在图7中把图形补画完整；‎ ‎（2）由于图纸中圆的半径的值已看不清楚，根据上述信息（图纸中是坡面的坡度），求的值．‎ ‎22．已知点P（1，-2a）在二次函数y=ax2+6的图象上，并且点P关于x轴的对称点Q在反比例函数的图象上．（1）求此二次函数和反比例函数的解析式； （2）点（-1，4）是否同时在（1）中的两个函数图象上？ ‎ ‎23．在△ABC中，∠BAC=90°，点D、E、F分别为AB、BC、AC的中点，联结EF.（1）如图8，若点D为AB的中点，联结BF，过点D作DG∥BF交EF的延长线于G，联结AE、AG、CG.求证：四边形AECG是菱形.‎ ‎（2）如图9，若点D在BA的延长线上，且,求证：四边形BEFD为等腰梯形.‎ 图9‎ 图8‎ ‎24.如图，在坐标系xOy中，△ABC是等腰直角三角形，∠BAC=90°，A（1，0），B（0，2），抛物线 的图象过C点． （1）求抛物线的解析式； （2）平移该抛物线的对称轴所在直线l．当l移动到何处时，恰好将△ABC的面积分为相等的两部分？ （3）点P是抛物线上一动点，是否存在点P，使四边形PACB为平行四边形？若存在，求出P点坐标；若不存在，说明理由．‎ ‎25．已知，，（如图11）．是射线上的动点（点与点不重合），是线段的中点．‎ ‎（1）设，的面积为，求关于的函数解析式，并写出函数的定义域；‎ ‎（2）如果以线段为直径的圆与以线段为直径的圆外切，求线段的长；‎ ‎（3）联结，交线段于点，如果以为顶点的三角形与相似，求线段的长．‎ B A D M E C 图11‎ B A D C 备用图 ‎24.解：（1）如答图1所示，过点C作CD⊥x轴于点D，则∠CAD+∠ACD=90°。 ∵∠OBA+∠OAB=90°，∠OAB+∠CAD=90°，∴∠OAB=∠ACD，∠OBA=∠CAD。 ∵在△AOB与△CDA中，， ∴△AOB≌△CDA（ASA）。 ∴CD=OA=1，AD=OB=2。 ∴OD=OA+AD=3。 ∴C（3，1）。 ∵点C（3，1）在抛物线上，∴，解得：。 ∴抛物线的解析式为：。 （2）在Rt△AOB中，OA=1，OB=2，由勾股定理得：AB=。∴S△ABC=AB2=。 设直线BC的解析式为y=kx+b，∵B（0，2），C（3，1）， ∴，解得。∴直线BC的解析式为。 同理求得直线AC的解析式为：。 如答图1所示，设直线l与BC、AC分别交于点E、F， 则。 在△CEF中，CE边上的高h=OD﹣x=3﹣x．‎ 由题意得：S△CEF=S△ABC，即： EF•h=S△ABC。 ∴，整理得：（3﹣x）2=3。 解得x=3﹣或x=3+（不合题意，舍去）。 ‎ ‎∴当直线l解析式为x=3﹣时，恰好将△ABC的面积分为相等的两部分。 （3）存在。如答图2所示， 过点C作CG⊥y轴于点G，则CG=OD=3，OG=1，BG=OB﹣OG=1。 过点A作AP∥BC，且AP=BC，连接BP，则四边形PACB为平行四边形。 过点P作PH⊥x轴于点H，则易证△PAH≌△BCG。 ∴PH=BG=1，AH=CG=3，∴OH=AH﹣OA=2。∴P（﹣2，1）。 ∵抛物线解析式为：，当x=﹣2时，y=1，即点P在抛物线上。 ∴存在符合条件的点P，点P的坐标为（﹣2，1）．。‎ ‎25.解：（1）取中点，连结，‎ 为的中点，，．································ 1分 又，．·································································· 2分 ‎，得；··············································· 3分 ‎（2）过D作DP⊥BC，垂足为P，∠DAB=∠ABC=∠BPD=90°，‎ ‎∴四边形ABPD是矩形．‎ 以线段为直径的圆与以线段为直径的圆外切，‎ ‎， 又，∴DE=BE+AD-AB=x+4-2=x+2……4分 PD=AB=2，PE= x-4，DE2= PD2+ PE2，…………………………………………………5分 ‎∴（x+2）2=22+（x-4）2，解得：．‎ ‎∴线段的长为．…………………………………………………………………………6分 ‎（3）由已知，以为顶点的三角形与相似，‎ 又易证得．···································································· 7分 由此可知，另一对对应角相等有两种情况：①；②．‎ ‎①当时，，．．‎ ‎，易得．得；················································ 8分 ‎②当时，，．‎ ‎．又，．‎ ‎，即=，得x2=[22+（x-4）2]．‎ 解得，（舍去）．即线段的长为2．······································· 9分 综上所述，所求线段的长为8或2．‎ ‎25+.在△ABC中，∠ABC＝90°，AB＝4，BC＝3，O是边AC上的一个动点，过点O作OD⊥AB于点D，以O为圆心OD为半径作半圆，交线段OC于点E，作EP⊥ED，交射线AB于点P，交射线CB于点F。‎ （1） 如图8，求证：△ADE∽△AEP；‎ （2） 设OA＝x，AP＝y，求y关于x的函数解析式，并写出它的定义域；‎ （3） 当BF＝1时，求线段AP的长.‎