2012年广州中考数学试卷及答案(含压轴题详细答案) 11页

‎ 2012年广州市初中毕业生学业考试 数 学 ‎ 本试卷分选择题和非选择题两部分，共三大题25小题，共4页，满分150分，考试用时120分钟 注意事项：‎ ‎1．答卷前，考生务必在答题卡第1面、第3面、第5面上用黑色字迹的钢笔或签字笔填写自已的考生号、姓名；填写考场试室号、座位号，再用2B铅笔把对应这两个号码的标号涂黑。‎ ‎2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号，不能答在试卷上。‎ ‎3．非选择题必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用2B铅笔画图，答案必须写在答题卡各题目指定区域内的相应位置上，如需改动，先划掉原来的答案，然后再写上新的答案，改动的答案也不能超出指定的区域，不准使用铅笔，圆珠笔和涂改液，不按以上要求作答的答案无效。‎ ‎4．考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回。‎ 第一部分 选择题 （共30分）‎ 一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的。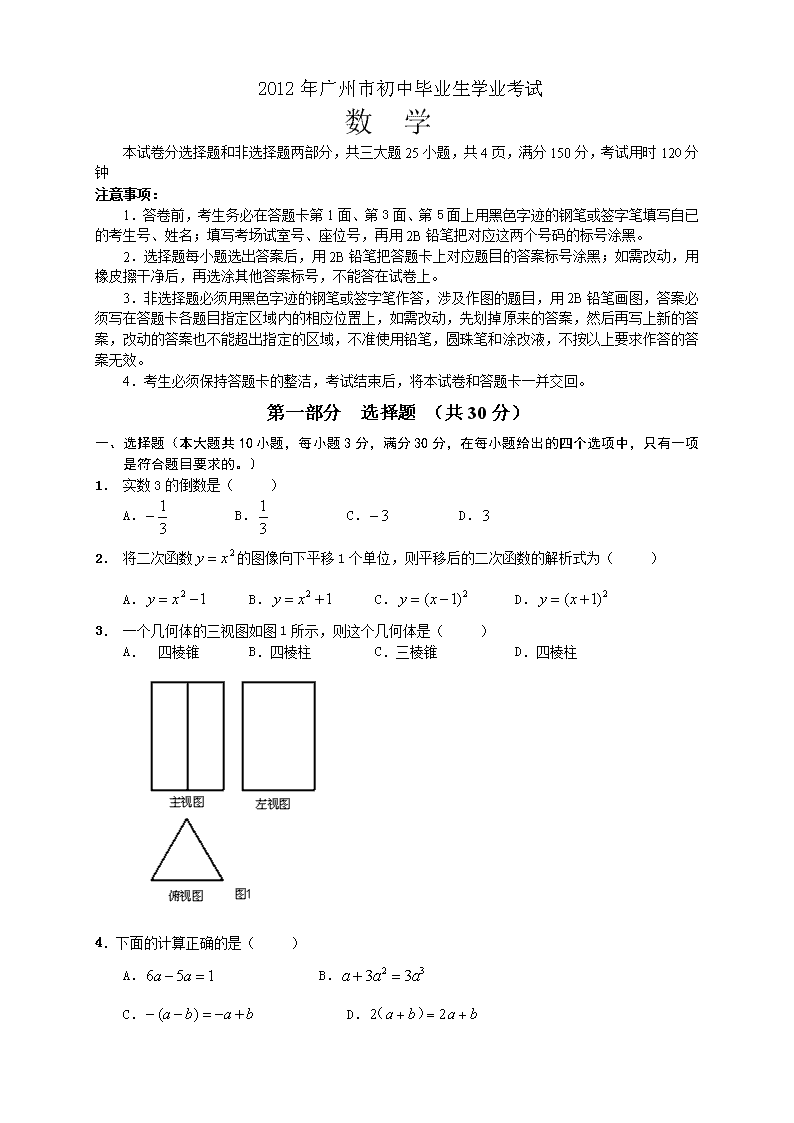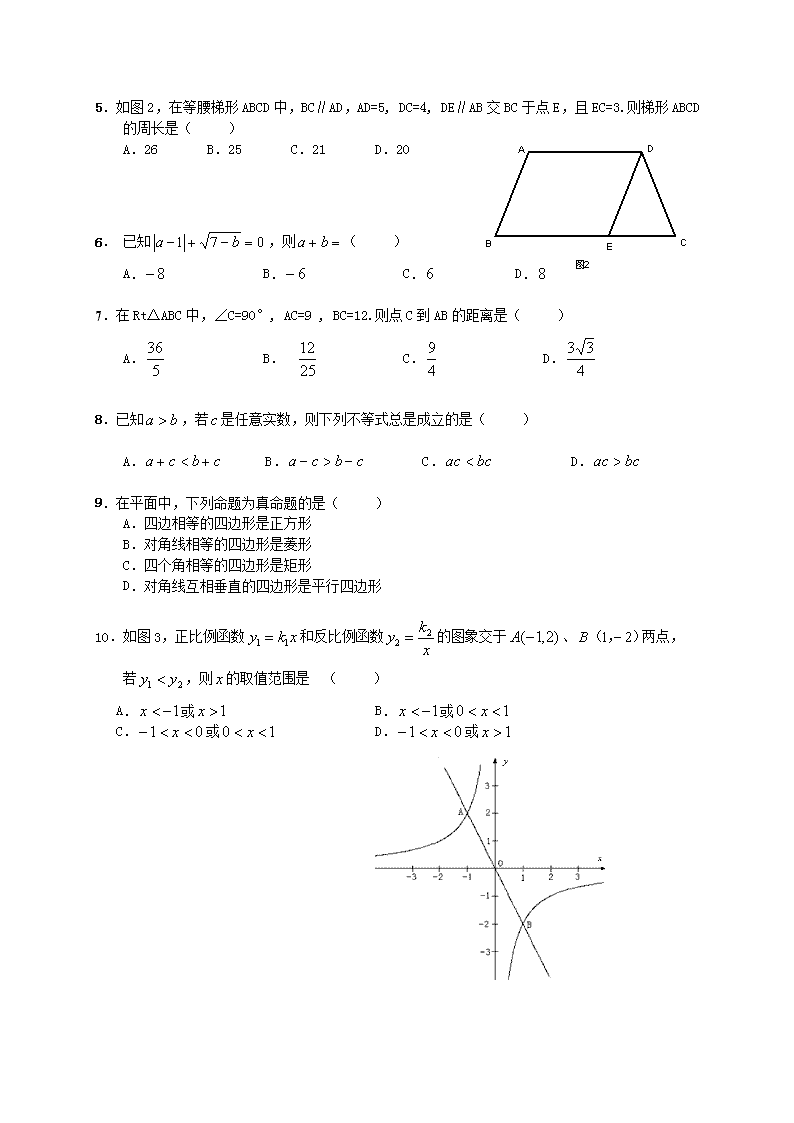）‎ ‎1． 实数3的倒数是（ ）‎ A． B． C． D．‎ ‎2． 将二次函数的图像向下平移1个单位，则平移后的二次函数的解析式为（ ）‎ A． B． C． D．‎ ‎3． 一个几何体的三视图如图1所示，则这个几何体是（ ） ‎ A． 四棱锥 B．四棱柱 C．三棱锥 D．四棱柱 ‎ ‎4．下面的计算正确的是（ ）‎ A． B． ‎ C． D．‎ ‎5．如图2，在等腰梯形ABCD中，BC∥AD，AD=5, DC=4, DE∥AB交BC于点E，且EC=3.则梯形ABCD ‎ 的周长是（ ）‎ A．26 B．25 C．21 D．20‎ ‎6． 已知，则（ ）‎ A． B． C． D．‎ ‎7．在Rt△ABC中，∠C=90°, AC=9 , BC=12.则点C到AB的距离是（ ）‎ A． B． C． D．‎ ‎8．已知，若是任意实数，则下列不等式总是成立的是（ ）‎ A． B． C． D．‎ ‎9．在平面中，下列命题为真命题的是（ ）‎ A．四边相等的四边形是正方形 ‎ B．对角线相等的四边形是菱形 C．四个角相等的四边形是矩形 D．对角线互相垂直的四边形是平行四边形 10． 如图3，正比例函数和反比例函数的图象交于、两点，‎ ‎ 若，则的取值范围是 （ ） ‎ ‎ A．或 B．或 ‎ ‎ C．或 D．或 ‎ 第二部分 非选择题 （共120分）‎ 二、填空题（本大题共6小题，每小题3分，满分18分.）‎ ‎11．已知∠ABC=30°, BD是∠ABC的平分线，则∠ABD=_______度．‎ ‎12．不等式的解集是_______．‎ ‎13．分解因式：=_______．‎ ‎14．如图4，在等边△ABC中，AB=6，D是BC上一点.且BC=3BD，△ABD绕点A旋转后的得到△ACE.‎ ‎ 则CE的长为_______．‎ ‎15．已知关于的一元二次方程有两各项等的实数根，则的值为_______．‎ ‎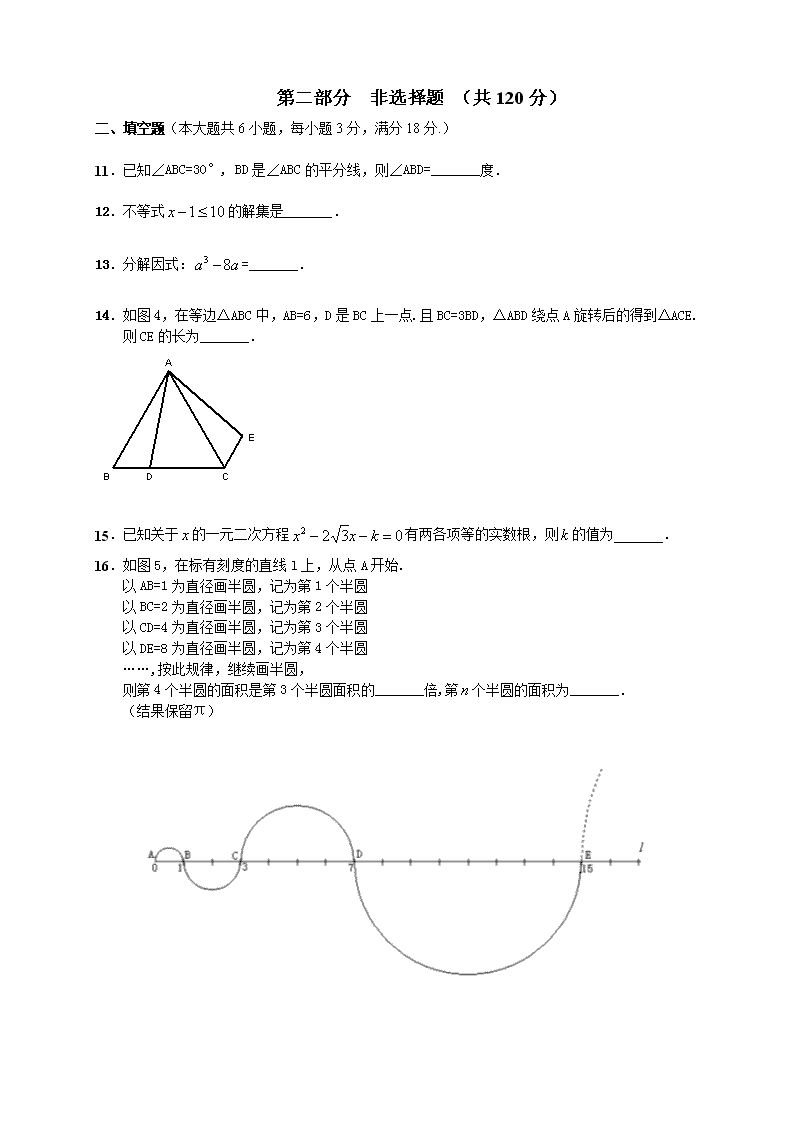16．如图5，在标有刻度的直线l上，从点A开始.‎ ‎ 以AB=1为直径画半圆，记为第1个半圆 ‎ 以BC=2为直径画半圆，记为第2个半圆 ‎ 以CD=4为直径画半圆，记为第3个半圆 ‎ 以DE=8为直径画半圆，记为第4个半圆 ‎ ‎……,按此规律，继续画半圆，‎ 则第4个半圆的面积是第3个半圆面积的_______倍,第个半圆的面积为_______．‎ ‎（结果保留π） ‎ 三、解答题（本大题共9小题，满分102分，解答应写出文字说明、证明过程或演算步骤）‎ ‎17．（本小题满分9分）‎ ‎ 解方程组：‎ ‎18．（本小题满分9分）‎ ‎ 如图6，点D在AB上，点E在AC上，AB=AC，∠B=∠C.‎ 求证：BE=CD ‎19．（本小题满分10分）‎ ‎ 广州市努力改善空气质量，近年来空气质量明显好转，根据广州市环境局公布的2006～2010这五年的全年空气质量优良的天数，绘制折线图如图7，根据图中信息回答：‎ ‎ （1）这五年的全年空气质量是优良的天数的中位数是_______ ；极差是_______ ；‎ ‎ （2） 这五年的全年空气质量优良天数与它的前一年相比较，增加最多的是______年（填写年份）；‎ ‎ （3）求这五年的全年空气质量优良天数的平均数.‎ ‎20．（本小题满分10分）‎ ‎ 已知，求的值.‎ ‎21．（本小题满分12分）‎ ‎ 甲、乙两个袋中均装有三张除所标数值外完全相同的卡片，甲袋中的三张卡片上的所标的数值分别为、、,乙袋中的三张卡片上所标的数值分别为、、 ，先从甲袋中随机取一张卡片，用表示取出的卡片上标的数值，再从乙袋从随机取出一张卡片，用表示取出的卡片上标的数值.把、分别作为点A的横坐标、纵坐标.‎ ‎（1）用适当的方法写出点的所有情况；‎ ‎（2）求点A落在第三象限的概率 .‎ ‎22．（本小题满分12分）‎ ‎ 如图8，⊙P的圆心为，半径为3，直线MN过点且平行于轴，点N在点M的上方.‎ ‎（1）在图中作出⊙P关于轴的对称的⊙P’，根据作图直接写出⊙P’与直线MN的位置关系 ；‎ ‎（2）若点N在（1）中的⊙P’上，求PN的长.‎ ‎23．（本小题满分12分） ‎ 某城市居民用水实施阶梯收费.每户每月用水量如果未超过20吨，按每吨1.9元收费：每户每月用水量如果超过20吨，未超过的部分仍按每吨1.9元收费，超过的部分则按每吨2.8元收费.设某户每月用水量为吨，应收水费为元。‎ （1） 分别写出每月用水量未超过20吨和超过20吨时，与间的函数关系式；‎ ‎（2）若该城市某户5月份水费平均为每吨2.2元，求该户5月份用水多少吨？‎ ‎24．（本小题满分14分）‎ 如图9，抛物线与轴交于A、B两点（点A在点B的左侧），与轴 交于点C ‎（1）求点A、B的坐标；‎ ‎（2）设D为已知抛物线的对称轴上任意一点，当△ACD的面积等于△ACB的面积时，求点D的 ‎ 坐标；‎ ‎（3）当直线l过点，M为直线l上的动点，当以A、B、M为顶点所作的直角三角形 ‎ 有且只有三个时，求直线l的解析式.‎ ‎25．（本小题14分）‎ ‎ 如图10，在平行四边形ABCD中，AB=5，BC=10，F为AD中点，CE⊥AB于点E，‎ ‎ 设∠ABC= ‎ （1） 当时，求CE的长；‎ （2） 当 ‎ ①是否存在正整数，使得∠EFD=∠AEF？若存在，求出的值；若不存在，请说明理由 ‎ ②连接CF，当取最大值时，求tan∠DCF的值.‎ ‎ ‎ ‎2012广州中考数学试题 参考答案 一、选择题：‎ ‎1-5：BADCC 6-10：DABCD 二、填空题：‎ ‎11-16： ‎ 三、解答题：‎ ‎17、‎ 解：‎ ‎18、‎ 解：略 ‎ ‎19、‎ 解：（1）345 24 （2） 2008 （3） 342.2 ‎ ‎20、‎ 解：‎ ‎21、‎ 解：(1) (2) ‎ ‎22、‎ 解：(1)图略。相交。 （2） PN=‎ ‎23、‎ 解：（1） （2）30‎ ‎24、解：‎ ‎（1）令y=0，解方程得 所以A（-4,0） B（2,0）‎ ‎（2）∵设直线AC与抛物线对称轴交于E点 又∵抛物线对称轴 易得E（，0）‎ ‎ ∴S△ADE+S△CDE=S△ACD 又∵S△ABC=AB··=9‎ ‎∴当S△ABC= S△ACD时 有 DE·4·=9‎ ‎∴ DE=‎ 则或 ∴D（-1）或者D（-1）‎ （1） 如图所示，△ABM为Rt三角形有三种情况：MA⊥AB，MB⊥AB，MA⊥MB 当MA⊥MB时，以AB为直径的圆与直线L相切与M点。‎ 连接，设直线L与Y轴交于H点。‎ ‎_‎ C ‎_‎ A ‎_‎ B ‎_‎ H ‎_‎ L ‎_‎ M ‎_‎ M ‎_‎ M ‎_‎ L ‎_‎ O ‎_‎ M ‎_‎ E ‎_‎ O ‎1‎ ‎∴=3，=5ME=4‎ 易证：△ △HOE ‎∴HO=3‎ ‎∴H（0,3）或者H（0，-3）‎ 则直线HE为 或者 ‎25、解：‎ ‎（1）∵∠a=60°‎ 又∵CE⊥AB ‎∴∠ECB=30°‎ ‎∴EB=CB=5‎ ‎∴CE=‎ ‎（2）‎ ‎1、存在。如图，延长CF至FG，使得CF=FG，连结AG。过F作FH∥AB交BC于H点。‎ ‎∵CF=FG，AF=FD，∠CFD=∠AFG △AFG △DFC ‎∴EF=GC=FC 由∵FH∥AB，CE⊥AB ‎∴CE⊥FH ‎∴∠EFH=∠CFH 又∵四边形ABHF与四边形CDFH为平行四边形 ‎∴∠CFD=∠CFH ‎∴∠AEF=∠EFH=∠HFC=∠CFD ‎∴k=3‎ ‎2、设EB=x，由1得GA=5，GE=10-x ‎∴‎ 又∵CF=GC ‎ ‎∴‎ ‎∴==‎ ‎∴当x=时，取到最大值 即E点在AB中点。‎ ‎∴tan∠DCF==‎