湘教版中考数学模拟试题含答案 9页

‎2011年初中毕业学业水平考试模拟试卷（二）‎ 数 学 一、选择题（请将你认为正确的选择支的代号填在下面的表格里。每小题3分，共30分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 ‎1、2007年中国月球探测工程的“嫦娥一号”卫星将发射升空飞向月球。已知地球距离月球表面约为384000千米，那么这个距离用科学记数法（保留三个有效数字）表示应为（ ）‎ A、3.84×千米 B、3.84×千米 C、3.84×千米 D、38.4×千米 ‎2、已知⊙O1的直径为‎6cm，⊙O2的直径R为‎8cm，两圆的圆心距O1O2 为‎1cm，则这两圆的位置关系是（ ）‎ A、内切 B、外切 C、相交 D、内含 ‎ ‎3、甲，乙超市为了促销一种定价相同的商品，甲超市连续两次降价10﹪，乙超市一次性降价20﹪，在哪家超市购买此种商品合算（ ）‎ A、甲 B、乙 C 、同样 D、与商品价格相关 ‎4、如下图是由一些完全相同的小立方块搭成的几何体的三种视图，那么搭成这个几何体所用的小立方块的个数是（ ）‎ A、5个 B、6个 C、7个 D、8个 ‎5、下列运算正确的是（ ）‎ A、 B、 C、 D、‎ ‎6、下列事件中，不可能事件是（ ）‎ A、掷一枚六个面分别刻有1～6数码的均匀正方体骰子，向上一面的点数是“‎‎5”‎ B、任意选择某个电视频道，正在播放动画片 C、肥皂泡会破碎 D、在平面内，度量一个三角形的内角度数，其和为360°‎ ‎7、已知代数式与是同类项，那么a、b的值分别是（ ）‎ 图1‎ A、 B、 C、 D、‎ ‎8、把一张长方形的纸片按如图1所示的方式折叠，EM、FM为折痕，折叠后的C点落在或的延长线上，那么∠EMF的度数是（ ）‎ A、85° B、90° C、95° D、100°‎ 图2‎ ‎9、如图2，梯子跟地面的夹角为∠A，关于∠A的三角函数值与梯子的倾斜程度之间，‎ 叙述正确的是（ ）‎ ‎ A、sinA的值越小，梯子越陡 B、cosA的值越小，梯子越陡 ‎ C、tanA的值越小，梯子越陡 D、陡缓程度与上A的函数值无关 图3‎ ‎10、直线（， 为常数）的图象如图3，‎ 化简：︱︱－得　　（　　　　）‎ Ａ、　　B、‎5　‎　　C、－１　　 D、‎ 图4‎ 二、填空题（把正确的答案填在相应的横线上，每小题3分，共24分）‎ ‎11、函数的自变量x的取值范围是______________。‎ ‎12、把分解因式的结果是______________。‎ ‎13、如图（4），圆锥底面半径为，母线长为，则圆锥侧面展开 图的圆心角为 。‎ ‎14、已知等腰的腰AB＝AC＝‎10cm，，底边BC=‎12cm,则的平分线的长是 cm.‎ ‎15、不等式组 的解集是________________。‎ ‎16、两个相似三角形的周长之比为4:9，那么它们的相似比为________________‎ 图5‎ ‎17、如图５，在等腰梯形ABCD中，AD∥BC，AB≠AD，对角线AC、BD相交于点O。如下四个结论：‎ ① 梯形ABCD是轴对称图形； ②∠DAC=∠DCA；‎ ‎③△AOB≌△DOC； ④△AOD∽△BOC 请把其中错误结论的序号填在横线上：___________。‎ ‎18、如图6，如果以正方形ABCD的对角线AC为边作第二个正方 图6‎ 形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下 去，…，已知正方形ABCD的面积为1，按上述方法所作的正 方形的面积依次为，，…..,（n为正整数），那么第8个正方 形的面积 ＝_______。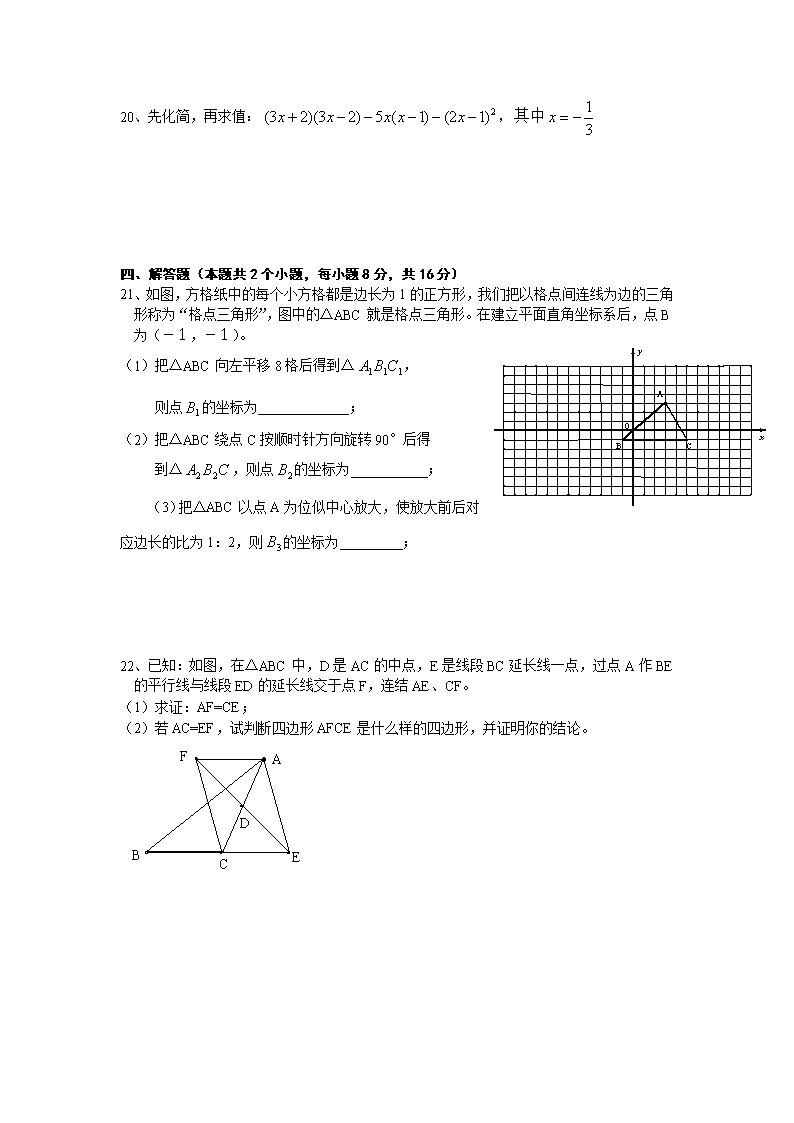‎ 三、解答题（本题共2个小题，每小题6分，共12分）‎ ‎19、计算：‎ ‎20、先化简，再求值：，其中 四、解答题（本题共2个小题，每小题8分，共16分）‎ ‎21、如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的△ABC就是格点三角形。在建立平面直角坐标系后，点B为（－１，－１）。‎ ‎（1）把△ABC向左平移8格后得到△，‎ 则点的坐标为 ；‎ ‎（2）把△ABC绕点C按顺时针方向旋转90°后得 到△，则点的坐标为 ；‎ ‎（3）把△ABC以点A为位似中心放大，使放大前后对应边长的比为1：2，则的坐标为 ； ‎ ‎22、已知：如图，在△ABC中，D是AC的中点，E是线段BC延长线一点，过点A作BE的平行线与线段ED的延长线交于点F，连结AE、CF。‎ ‎（1）求证：AF=CE；‎ ‎（2）若AC=EF，试判断四边形AFCE是什么样的四边形，并证明你的结论。‎ 五、解答题（本题共2个小题，每小题9分，共18分）‎ ‎23、如图所示，在平面直角坐标系中，抛物线的顶点P到x轴的距离是9，抛物线与x轴交于O、M两点，OM=6；矩形ABCD的边BC在线段OM上，点A、D在抛物线上。‎ ‎ （1）P点的坐标 、M点的坐标 ；‎ ‎（2）求抛物线的解析式；‎ ‎（3）设矩形ABCD的周长为，，求与的关系式，并求的最大值；‎ ‎24、某蔬菜公司收购蔬菜进行销售的获利情况如下表所示：‎ 销售方式 直接销售 粗加工后销售 精加工后销售 每吨获利（元）‎ ‎100‎ ‎250‎ ‎450‎ 现在该公司收购了140吨蔬菜，已知该公司每天能精加工蔬菜6吨或粗加工蔬菜16吨（两种加工不能同时进行）。‎ ‎（1）如果要求在18天内全部销售完这140吨蔬菜请完成下列表格：‎ 销售方式 全部直接销售 全部粗加工后销售 尽量精加工，剩余部分直接销售 获利（元）‎ ‎（2）如果精加工一部分，剩余的粗加工，要求在15天内刚好加工完140吨蔬菜，则应如何分配加工时间？‎ ‎（3）如果要求蔬菜都要加工后销售，且公司获利不能少于42200元，问至少将多少吨蔬菜进行精加工？‎ 六、解答题（本题共2个小题，每小题10分，共20分）‎ ‎25、如图：在等腰梯形ABCD中，AB∥CD，∠A=60°，AB=‎20cm，CD=‎8cm。等边三角形PMN的边长MN=‎20cm，A点与N点重合，MN和AB在一条直线上，设等腰梯形ABCD不动，等边三角形PMN沿AB所在的直线匀速向右移动，直到点M与点B重合为止。‎ ‎ （1）等边三角形PMN在整个运动过程中与等腰梯形ABCD重叠部分的形状由 形变为 形，‎ 再变为 形；‎ ‎ （2）设等边三角形移动距离x（cm）时，等边三角形PMN与等腰梯形ABCD重叠的部分的面积为y，求y与x之间的函数关系式；‎ ‎ ‎ ‎ ‎ ‎26、已知：如图所示，抛物线的顶点C在以D（―2，―2）为圆心，4为半径的圆上，且经过⊙D与轴的两个交点A、B，连结AC、BC、OC。 ‎ ‎（1）求点C的坐标；‎ ‎（2）求图中阴影部分的面积；‎ ‎（3）在抛物线上是否存在点P，使DP所在直线平分线段OC？若存在，求出点P的坐标；若不存在，请说明理由。‎ ‎ ‎ ‎2011年初中毕业学业水平考试模拟试卷（二）‎ 数学参考答案 一、选择题（请将你认为正确的选择支的代号填在下面的表格里。每小题3分，共30分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B A B D C D A B B D 二、填空题（把正确的答案填在相应的横线上，每小题3分，共24分）‎ ‎11、x≥1 　　12、 　　13、90° 　　　 14、8 ‎ ‎ 15、无解 　　 16、4:9 　　　　　 17、（2） 　　　 18、128‎ 三、解答题（本题共2个小题，每小题6分，共12分）‎ ‎19． （每对一个知识点给1分） ‎ ‎20．原式==－8　（三个整式的运算对一个给1分，合并正确给2分，代入求值1分） ‎ ‎ ‎ 四、解答题（本题共2个小题，每小题8分，共16分）‎ ‎21．（1）（-9，-1）（2）（5，5） （3）（-5，-5）或（5，5）（每问2分，第3问答对一个就给2分） ‎ ‎22．每问3分。答案略。 ‎ 五、解答题（本题共2个小题，每小题9分，共18分）‎ ‎23．（1）P（3，9） M（0，6） -------- 2分 （2） --------------3分 ‎ ‎ 　（3） -------2分，当x=2时，最大值为20-----------1分 六、解答题（本题共2个小题，每小题10分，共20分）‎ ‎25．（1）等边三角形、等腰梯形、等边三角形----------3分 ‎ （2） 下结论1分。‎ ‎26．解：（1）如图，作CH⊥轴，垂足为H， ∵直线CH为抛物线对称轴，∴H为AB的中点。…1分 ‎∴CH必经过圆心D（―2，―2）。∵DC=4，∴CH=6 ∴C点的坐标为（―2，―6）。 …3分 ‎ （2）连结AD，在Rt△ADH中，AD=4，DH=2，∴，。。。4分 ‎ ∴ ‎ ‎ ∴ ‎ ‎∴阴影部分的面积 ……… 6分 ‎ （3）又∵，H点坐标为（―2，0），H为AB的中点，‎ ‎∴A点坐标为（―2―2，0），B点坐标为（，0）。 ………7分 又∵抛物线顶点C的坐标为（―2，―6），设抛物线解析式为 ‎∵B（，0）在抛物线上， ∴，解得。‎ ‎∴抛物线的解析式为 …………8分 设OC的中点为E，过E作EF⊥轴，垂足为F，连结DE，‎ ‎∵CH⊥轴，EF⊥轴，∴CH∥EF ∵E为OC的中点，‎ ‎∴。‎ 即点E的坐标为（―1，―3）。 设直线DE的解析式为，‎ ‎∴，解得，∴直线DE的解析式为。 ……………9分 若存在P点满足已知条件，则P点必在直线DE和抛物线上。 设点P的坐标为（，），‎ ‎∴，即点P坐标为（，）， ∴，‎ 解这个方程，得， ∴点P的坐标为（0，－4）和（－6，2）。 ……10分