中考数学 辅助线 30页

1 几何辅助线（图）作法探讨 一些几何题的证明或求解，由原图形分析探究，有时显得十分复杂，若通过适当的变换，即添加适当的辅助线 （图），将原图形转换成一个完整的、特殊的、简单的新图形，则能使原问题的本质得到充分的显示，通过对新图形 的分析，原问题顺利获解。有许多初中几何常见辅助线作法歌诀，下面这一套是很好的： 人说几何很困难，难点就在辅助线。辅助线，如何添？把握定理和概念。 还要刻苦加钻研，找出规律凭经验。 三角形 图中有角平分线，可向两边作垂线。也可将图对折看，对称以后关系现。 角平分线平行线，等腰三角形来添。角平分线加垂线，三线合一试试看。 线段垂直平分线，常向两端把线连。要证线段倍与半，延长缩短可试验。 三角形中两中点，连接则成中位线。三角形中有中线，延长中线等中线。 四边形 平行四边形出现，对称中心等分点。梯形里面作高线，平移一腰试试看。 平行移动对角线，补成三角形常见。证相似，比线段，添线平行成习惯。 等积式子比例换，寻找线段很关键。直接证明有困难，等量代换少麻烦。 斜边上面作高线，比例中项一大片。 圆 半径与弦长计算，弦心距来中间站。圆上若有一切线，切点圆心半径连。 切线长度的计算，勾股定理最方便。要想证明是切线，半径垂线仔细辨。 是直径，成半圆，想成直角径连弦。弧有中点圆心连，垂径定理要记全。 圆周角边两条弦，直径和弦端点连。弦切角边切线弦，同弧对角等找完。 要想作个外接圆，各边作出中垂线。还要作个内切圆，内角平分线梦圆。 如果遇到相交圆，不要忘作公共弦。内外相切的两圆，经过切点公切线。 若是添上连心线，切点肯定在上面。要作等角添个圆，证明题目少困难。 辅助线，是虚线，画图注意勿改变。假如图形较分散，对称旋转去实验。 基本作图很关键，平时掌握要熟练。解题还要多心眼，经常总结方法显。 切勿盲目乱添线，方法灵活应多变。分析综合方法选，困难再多也会减。 虚心勤学加苦练，成绩上升成直线。 2 在几何题的证明或求解时，需要构成一些基本图形来求证（解）时往往要通过添加辅助线（图）来形成，添加 辅助线（图），构成的基本图形是结果，构造的手段是方法。 笔者从作辅助线的结果和方法两方面将几何辅助线（图）作法归纳为结果―――（1）构造基本图形；（2）构 造等腰（边）三角形：（3）构造直角三角形；（4）构造全等三角形；（5）构造相似三角形；（6）构造特殊四边 形；（7）构造圆的特殊图形；方法―――（8）基本辅助线；（ 9）截取和延长变换；（10）对称变换；（11）平移 变换；（12）旋转变换。下面通过近年全国各地中考的实例探讨其应用。 一、构造基本图形：每个几何定理都有与它相对应的几何图形，我们把它叫做基本图形，添辅助线往往是具有 基本图形的性质而基本图形不完整时补完整基本图形。如平行线，垂直线，直角三角形斜边上中线，三角形、四边 形的中位线等。等腰（边）三角形、直角三角形、全等三角形、相似三角形、特殊四边形和圆的特殊图形也都是基 本图形，但我们后面把它们单独表述。 典型例题： 例 1.（2012 四川内江 3 分）如图， 【 】 A. B. C. D. 例 2.（2012 江苏宿迁 3 分）已知点 E，F，G，H 分别是四边形 ABCD 的边 AB，BC，CD，DA 的 中点，若 AC⊥BD，且 AC≠BD，则四边形 EFGH 的形状是 ▲ .（填“梯形”“矩形”“菱形” ） 【答案】矩形。 【考点】三角形中位线定理，矩形的判定。 【分析】如图，连接 AC，BD。 ∵E，F，G，H 分别是 AB，BC，CD，DA 的中点， ∴根据三角形中位线定理，HE∥AB∥GF，HG∥AC∥EF。 又∵AC⊥BD，∴∠EHG=∠HGF=∠GFE=∠FEH=900。 ∴四边形 EFGH 是矩形。 且∵AC≠BD，∴四边形 EFGH 邻边不相等。 ∴四边形 EFGH 不可能是菱形。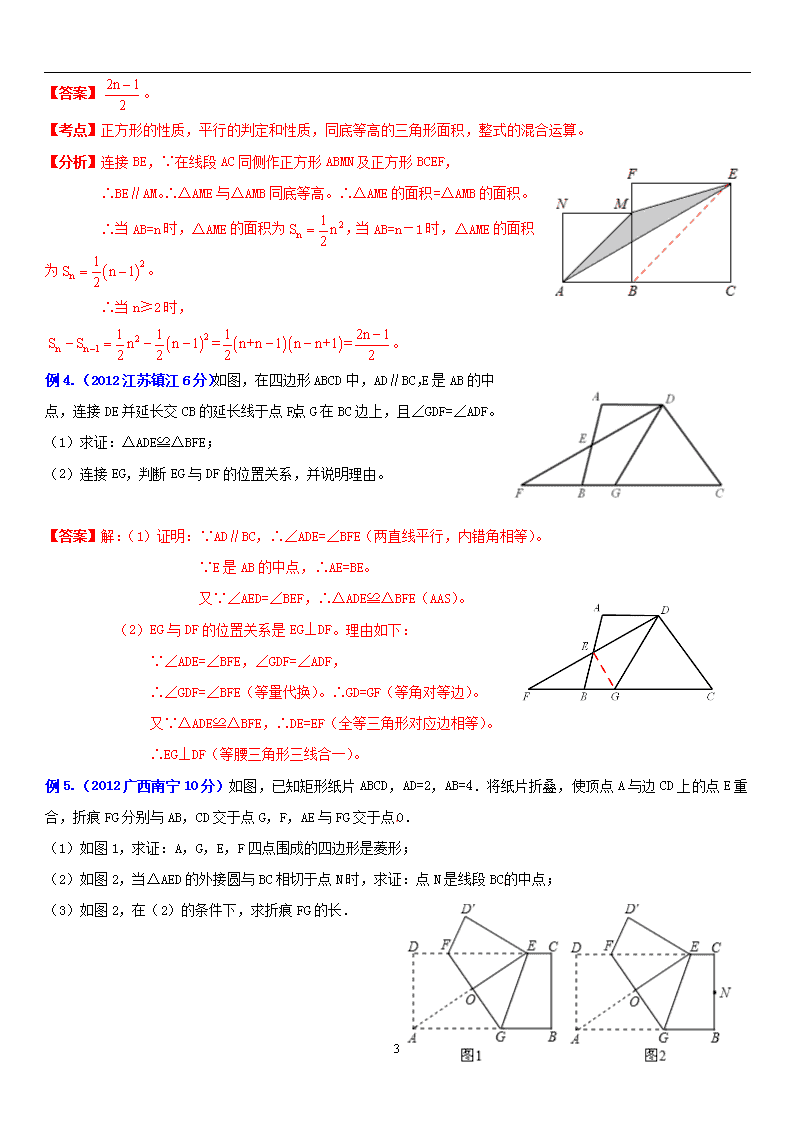 例 3.（2012 湖北天门、仙桃、潜江、江汉油田 3 分）如图，线段 AC=n+1（其中 n 为正整数），点 B 在线段 AC 上， 在线段 AC 同侧作正方形 ABMN 及正方形 BCEF，连接 AM、ME、EA 得到△AME．当 AB=1 时，△AME 的面积记为 S1；当 AB=2 时，△AME 的面积记为 S2；当 AB=3 时，△AME 的面积记为 S3；…；当 AB=n 时，△AME 的面积记为 Sn．当 n≥2 时， Sn﹣Sn﹣1=　 ▲ 　． =∠=∠=∠ 3,1402,651,// 00 则ba 0100 0105 0110 0115 3 【答案】 。 【考点】正方形的性质，平行的判定和性质，同底等高的三角形面积，整式的混合运算。 【分析】连接 BE，∵在线段 AC 同侧作正方形 ABMN 及正方形 BCEF， ∴BE∥AM。∴△AME与△AMB 同底等高。∴△AME 的面积=△AMB 的面积。 ∴当 AB=n 时，△AME 的面积为 ，当 AB=n－1 时，△AME 的面积 为 。 ∴当 n≥2 时， 。 例 4.（2012 江苏镇江 6 分）如图，在四边形 ABCD 中，AD∥BC，E 是 AB 的中 点，连接 DE 并延长交 CB 的延长线于点 F，点 G 在 BC 边上，且∠GDF=∠ADF。 （1）求证：△ADE≌△BFE； （2）连接 EG，判断 EG 与 DF 的位置关系，并说明理由。 【答案】解：（1）证明：∵AD∥BC，∴∠ADE=∠BFE（两直线平行，内错角相等）。 ∵E 是 AB 的中点，∴AE=BE。 又∵∠AED=∠BEF，∴△ADE≌△BFE（AAS）。 （2）EG 与 DF 的位置关系是 EG⊥DF。理由如下： ∵∠ADE=∠BFE，∠GDF=∠ADF， ∴∠GDF=∠BFE（等量代换）。∴GD=GF（等角对等边）。 又∵△ADE≌△BFE，∴DE=EF（全等三角形对应边相等）。 ∴EG⊥DF（等腰三角形三线合一）。 例 5.（2012 广西南宁 10 分）如图，已知矩形纸片 ABCD，AD=2，AB=4．将纸片折叠，使顶点 A 与边 CD 上的点 E 重 合，折痕 FG 分别与 AB，CD 交于点 G，F，AE 与 FG 交于点 O． （1）如图 1，求证：A，G，E，F 四点围成的四边形是菱形； （2）如图 2，当△AED 的外接圆与 BC 相切于点 N 时，求证：点 N 是线段 BC的中点； （3）如图 2，在（2）的条件下，求折痕 FG 的长． 2n 1 2 − 2 n 1S n2 = ( )2 n 1S n 12 = − ( ) ( )( )22 n n 1 1 1 1 2n 1S S n n 1 = n+n 1 n n+1 =2 2 2 2− −− = − − − − 4 【答案】解：（1 ）由折叠的性质可得，GA=GE ，∠AGF=∠EGF， ∵DC∥AB，∴∠EFG=∠AGF。∴∠EFG=∠EGF。∴EF=EG=AG。 ∴四边形 AGEF 是平行四边形（EF∥AG，EF=AG）。 又∵AG=GE，∴四边形 AGEF 是菱形。 （2）连接 ON， ∵△AED 是直角三角形，AE 是斜边，点 O 是 AE 的中点， △AED 的外接圆与 BC 相切于点 N， ∴ON⊥BC。 ∵点 O 是 AE 的中点，∴ON 是梯形 ABCE 的中位线。 ∴点 N 是线段 BC 的中点。 （3）∵OE、ON 均是△AED 的外接圆的半径，∴OE=OA=ON=2。∴AE=AB=4。 在 Rt△ADE 中，AD=2，AE=4，∴∠AED=30°。 在 Rt△OEF 中，OE=2，∠AED=30°，∴ 。∴FG= 。 二、构造等腰（边）三角形：当问题中出现一点发出的二条相等线段时往往要补完整等腰（边）三角形；出现 角平分线与平行线组合时可延长平行线与角的二边相交得等腰（边）三角形。通过构造等腰（边）三角形，应用等 腰（边）三角形的性质得到一些边角相等关系，达到求证（解）的目的。 典型例题： 例 1. （2012 浙江丽水、金华 4 分）如图，在等腰△ABC 中，AB＝AC，∠BAC＝50°．∠BAC 的平分 线与 AB 的中垂线交于点 O，点 C 沿 EF 折叠后与点 O 重合，则∠CEF 的度数是　 ▲ 　． 【答案】50°。 连接 BO，∵AB＝AC，AO 是∠BAC 的平分线，∴AO 是 BC 的中垂线。 ∴BO＝CO。∵∠BAC＝50°，∠BAC 的平分线与 AB 的中垂线交于点 O， ∴∠OAB＝∠OAC＝25°。∵等腰△ABC 中， AB＝AC，∠BAC＝50°，∴∠ABC＝∠ACB＝65° 。 ∴∠OBC＝65°－25°＝40°。∴∠OBC＝∠OCB＝40°。 ∵点 C 沿 EF 折叠后与点 O 重合，∴EO＝EC，∠CEF＝∠FEO。 ∴∠CEF＝∠FEO＝（1800－2×400）÷2＝50°。 例 2.（2012 甘肃白银 10 分）如图，已知△ABC 是等边三角形，点 D、F 分别在线段 BC、AB 上，∠EFB=60°， DC=EF． 2 3OF 3 = 4 32OF 3 = 5 （1）求证：四边形 EFCD 是平行四边形； （2）若 BF=EF，求证：AE=AD． 【答案】证明：（1）∵△ABC 是等边三角形，∴∠ABC=60°。 ∵∠EFB=60°，∴∠ABC=∠EFB。∴EF∥DC（内错角相等，两直线平行）。 ∵DC=EF，∴四边形 EFCD 是平行四边形。 （2）连接 BE。 ∵BF=EF，∠EFB=60°，∴△EFB 是等边三角形。 ∴EB=EF，∠EBF=60°。 ∵DC=EF，∴EB=DC。∵△ABC 是等边三角形，∴∠ACB=60°，AB=AC。 ∴∠EBF=∠ACB。∴△AEB≌△ADC（SAS）。∴AE=AD。 例 3.（2011 上海 12 分）如图，在梯形 ABCD 中，AD//BC，AB＝DC，过点 D 作 DE⊥BC， 垂足为 E，并延长 DE 至 F，使 EF＝DE．联结 BF、CD、AC． （1）求证：四边形 ABFC 是平行四边形； （2）如果 DE2＝BE·CE，求证四边形 ABFC 是矩形． 【答案】解：（1）证明：连接 BD。 ∵梯形 ABCD 中，AD∥BC，AB=DC，∴AC=BD，∠ACB=∠DBC ∵DE⊥BC，EF=DE，∴BD=BF，∠DBC=∠FBC。 ∴AC=BF，∠ACB=∠CBF。∴AC∥BF。 ∴四边形 ABFC 是平行四边形； （2）∵DE2＝BE·CE，∴ 。 ∵∠DEB=∠DEC=90°，∴△BDE∽△DEC。∴∠CDE=∠DBE， ∴∠BFC=∠BDC=∠BDE＋∠CDE=∠BDE＋∠DBE=90°。 ∴四边形 ABFC 是矩形。 三、构造直角三角形：通过构造直角三角形，应用直角三角形的性质得到一些边角关系（勾股定理，两锐角互 余，锐角三角函数），达到求证（解）的目的。 典型例题： 例 1.（2012 广西柳州 3 分）已知：在△ABC 中，AC=a，AB 与 BC 所在直线成 45°角，AC 与 BC 所在直 线形成的夹角的余弦值为 （即 cosC= ），则 AC 边上的中线长是 ▲ ． DE CE BE DE = 2 55 2 55 6 【答案】 或 a。 【分析】分两种情况： ①△ABC 为锐角三角形时，如图 1，BE 为 AC 边的中线。 作△ABC 的高 AD，过点 E 作 EF⊥BC 于点 F。 ∵在 Rt△ACD 中，AC=a，cosC= ， ∴CD= a，AD= a。 ∵在 Rt△ABD 中，∠ABD=45°，∴BD=AD= a。。∴BC=BD+CD= a。 ∵点 E 是 AC 的中点，EF∥AD，∴EF 是△ACD 的中位线。∴FC= DC= a，EF= AD= a。 ∴BF= a。 在 Rt△BEF 中，由勾股定理，得 。 ②△ABC 为钝角三角形时，如图 2，BE 为 AC 边的中线。 作△ABC 的高 AD。 ∵在 Rt△ACD 中，AC=a，cosC= ， ∴CD= a，AD= a。 ∵在 Rt△ABD 中，∠ABD=45°，∴BD=AD= a。∴BC= BD= a。 ∵点 E 是 AC 的中点，∴BE 是△ACD 的中位线。∴BE= AD= a。 综上所述，AC 边上的中线长是 或 a。 例 2. （2012 广西河池 3 分）如图，在矩形 ABCD 中，AD＞AB，将矩形 ABCD 折叠，使点 C 与点 A 重 合，折痕为 MN，连结 CN．若△CDN 的面积与△CMN 的面积比为 1︰4，则 的值为【 】 85 a10 5 10 2 55 2 55 5 5 5 5 3 5 5 1 2 5 5 1 2 5 10 2 55 22 2 2 22 5 17 85BE BF EF 5a a = a = a5 10 20 10   = + = +         2 55 2 55 5 5 5 5 5 5 1 2 5 10 85 a10 5 10 MN BM 7 A．2 B．4 C． D． 【答案】D。 过点 N 作 NG⊥BC 于 G， ∵四边形 ABCD 是矩形，∴四边形 CDNG 是矩形，AD∥BC。 ∴CD=NG，CG=DN，∠ANM=∠CMN。 由折叠的性质可得：AM=CM，∠AMN=∠CMN，∴∠ANM=∠AMN。 ∴AM=AN。 ∴AM=CM，∴四边形 AMCN 是平行四边形。 ∵AM=CM，∴四边形 AMCN 是菱形。 ∵△CDN 的面积与△CMN 的面积比为 1：4，∴DN：CM=1：4。 设 DN=x，则 AN=AM=CM=CN=4x，AD=BC=5x，CG=x。∴BM=x，GM=3x。 在 Rt△CGN 中， ， 在 Rt△MNG 中， ， ∴ 。故选 D。 例 3.（2012 北京市 5 分）如图，在四边形 ABCD 中，对角线 AC，BD 交于点 E，∠BAC=900，∠CED=450，∠DCE=900， DE= ，BE=2 ．求 CD 的长和四边形 ABCD 的面积． 【答案】解：过点 D 作 DH⊥AC， ∵∠CED=45°，DH⊥EC，DE= ，∴EH=DH=1。 又∵∠DCE=30°，∴DC=2，HC= 。 ∵∠AEB=45°，∠BAC=90°，BE=2 ， ∴AB=AE=2。∴AC=2+1+ =3+ 。 ∴ 。 【考点】勾股定理，含 30 度角的直角三角形的性质，等腰直角三角形的性质， 四、构造全等三角形：通过构造全等三角形，应用全等三角形对应边、角相等的性质，达到求证（解）的目的。 典型例题： 例 1. （2012 浙江绍兴 5 分）如图，在矩形 ABCD 中，点 E，F 分别在 BC，CD 上，将△ABE 沿 AE 折叠，使点 B 落在 AC 上的点 B′处，又将△CEF 沿 EF 折叠，使点 C 落在 EB′与 AD 的交点 C′处．则 BC：AB 的值为 ▲ 。 2 5 2 6 ( )22 2 2NG CN CG 4x x 15x= − = − = ( ) ( )222 2MN GM NG 3x 15x =2 6x= + = + MN 2 6x= =2 6BM x 2 2 2 3 2 3 3 ABCD 1 1 9 3 3S 2 3 3 1 3 3 2 2 2 += × × + + × × + =四 形 （ ） （ ）边 8 例 2.（2012 山东泰安 3 分）如图，AB∥CD，E，F 分别为 AC，BD 的中点，若 AB=5，CD=3，则 EF 的长是【 】 　　A．4　　B．3　　C．2　　D．1 【答案】D。 【考点】三角形中位线定理，全等三角形的判定和性质。 【分析】连接 DE 并延长交 AB 于 H， ∵CD∥AB，∴∠C=∠A，∠CDE=∠AHE。 ∵E 是 AC 中点，∴DE=EH。∴△DCE≌△HAE（AAS）。 ∴DE=HE，DC=AH。∵F 是 BD 中点，∴EF 是△DHB 的中位线。∴EF= BH。 ∴BH=AB﹣AH=AB﹣DC=2。∴EF=1。故选 D。 例 3.（2012 山东德州 12 分）如图所示，现有一张边长为 4 的正方形纸片 ABCD，点 P 为正方形 AD 边上的一点（不 与点 A、点 D 重合）将正方形纸片折叠，使点 B 落在 P 处，点 C 落在 G 处，PG 交 DC 于 H，折痕为 EF，连接 BP、BH． （1）求证：∠APB=∠BPH； （2）当点 P 在边 AD 上移动时，△PDH 的周长是否发生变化？并证明你的结论； （3）设 AP 为 x，四边形 EFGP 的面积为 S，求出 S 与 x 的函数关系式，试问 S 是 否存在最小值？若存在，求出这个最小值；若不存在，请说明理由． 1 2 9 【答案】解：（1）如图 1，∵PE=BE，∴∠EBP=∠EPB． 又∵∠EPH=∠EBC=90°， ∴∠EPH﹣∠EPB=∠EBC﹣∠EBP，即∠PBC=∠BPH。 又∵AD∥BC，∴∠APB=∠PBC。∴∠APB=∠BPH。 （2）△PHD 的周长不变为定值 8。证明如下： 如图 2，过 B 作 BQ⊥PH，垂足为 Q。 由（1）知∠APB=∠BPH， 又∵∠A=∠BQP=90°，BP=BP， ∴△ABP≌△QBP（AAS）。∴AP=QP，AB=BQ。 又∵AB=BC，∴BC=BQ。 又∵∠C=∠BQH=90°，BH=BH，∴△BCH≌△BQH（HL）。∴CH=QH。 ∴△PHD 的周长为：PD+DH+PH=AP+PD+DH+HC=AD+CD=8。 （3）如图 3，过 F 作 FM⊥AB，垂足为 M，则 FM=BC=AB。 又∵EF 为折痕，∴EF⊥BP。 ∴∠EFM+∠MEF=∠ABP+∠BEF=90°。∴∠EFM=∠ABP。 又∵∠A=∠EMF=90°，AB=ME，∴△EFM≌△BPA（ASA）。 ∴EM=AP=x． ∴在 Rt△APE 中，（4﹣BE）2+x2=BE2，即 。 ∴ 。 又∵四边形 PEFG 与四边形 BEFC 全等， ∴ 。 ∵ ，∴当 x=2 时，S 有最小值 6。 2xBE 2+ 8 = 2xCF BE EM 2+ x8 = − = − ( ) ( )2 221 1 x 1 1S BE CF BC= 4+ x 4= x 2x+8= x 2 +62 2 4 2 2  = ⋅ + ⋅ ⋅ − ⋅ − −    10 42< < 10 例 4. （2011 广西南宁 3 分）如图，在△ABC 中，∠ACB＝90º，∠A＝15º，AB＝8，则 AC·BC 的值为【 】 A．14 B．16 3 C．4 15 D．16 【答案】D。 【考点】全等三角形的判定和性质，锐角三角函数。 【分析】延长 BC 到点 D，使 CD＝CB，连接 AD，过点 D 作 DE⊥AB，垂足为点 E。则知 △ACD≌△ACB，从而由已知得∠CAD＝∠A＝15º，AD＝AB。因此，在Rt△ADE 中，AD＝ 8，∠BAD＝30º，∴DE＝AD·sin30º＝4。从而 S △ADE＝ ·AB·DE＝16，又 S △ADE＝ ·BD·AC＝ ·2BC·AC＝AC·BC，即 AC·BC＝16。 例 5. （2011 山东济南 3 分）如图，在△ABC 中，∠ACB＝90º，AC＞BC，分别以 AB、BC 、CA 为一边 向△ABC 外作正方形 ABDE、BCMN、CAFG，连接 EF、GM、ND，设△AEF、△BND、△CGM 的面积 分别为 S1、S2、S3，则下列结论正确的是【 】 A．S1＝S2＝S3 B．S1＝S2＜S3 C．S1＝S3＜S2 D．S2＝S3＜S1 【答案】A。 【分析】过点 D 作 DQ⊥MN 交 CB 的延长线于点 P，交 MN 的延长线于点 Q； 过点 E 作 ER⊥GF 交 CA 的延长线于点 S，交 GF 的延长线于点 R。 易证△CGM≌△CAB（SAS），即 S2＝S△ABC； 易证△PBD≌△CAB（AAS），∴BP=AC，即 S3 的底为 BN=BC，高为 BP=AC，∴S2＝S△ABC； 易证△SEA≌△CAB（AAS），∴AS=BC，即 S1 的底为 FA=CA，高为 AS=BC，∴S2＝S△ABC。 ∴S1＝S2＝S3＝S△ABC。故选 A。 例 6. （2011 山东德州 8 分）如图 AB=AC，CD⊥AB 于 D，BE⊥AC 于 E，BE 与 CD 相交于点 O． （1）求证 AD=AE； （2）连接 OA，BC，试判断直线 OA，BC 的关系并说明理由． 【答案】解：（1）证明：在△ACD 与△ABE 中， ∵∠A=∠A，∠ADC=∠AEB=90°，AB=AC， ∴△ACD≌△ABE（AAS）。∴AD=AE。 （2）在 Rt△ADO 与 Rt△AEO 中，∵OA=OA，AD=AE， 1 2 1 2 1 2 11 ∴△ADO≌△AEO（HL）。∴∠DAO=∠EAO。 即 OA 是∠BAC 的平分线。 又∵AB=AC，∴OA⊥BC。 五、构造相似三角形：通过构造相似三角形，应用相似三角形对应角相等、对应边成比例的性质，达到求证（解） 的目的。 典型例题： 例 1.（2012 湖北十堰 3 分）如图，矩形 ABCD 中，AB=2，AD=4，AC 的垂直平分线 EF 交 AD 于点 E、交 BC 于点 F，则 EF=　 ▲ 　． 【答案】 。 【分析】连接 EC，AC、EF 相交于点 O。 ∵AC 的垂直平分线 EF，∴AE=EC。 ∵四边形 ABCD 是矩形， ∴∠D=∠B=90°，AB=CD=2，AD=BC=4，AD∥BC。 ∴△AOE∽△COF。∴ 。 ∵OA=OC，∴OE=OF，即 EF=2OE。 在 Rt△CED 中，由勾股定理得：CE2=CD2+ED2，即 CE2=（4－CE）2+22，解得： CE= 。 ∵在 Rt△ABC 中，AB=2，BC=4，由勾股定理得：AC= ，∴CO= 。 ∵在 Rt△CEO 中，CO= ，CE= ，由勾股定理得：EO= 。∴EF=2EO= 。 例 2.（2012 天津市 10 分）已知一个矩形纸片 OACB，将该纸片放置在平面直角坐标系中，点 A（11，0），点 B（0， 6），点 P 为 BC 边上的动点（点 P 不与点 B、C 重合），经过点 O、P 折叠该纸片，得点 B′和折痕 OP．设 BP=t． （Ⅰ）如图①，当∠BOP=300 时，求点 P 的坐标； （Ⅱ）如图②，经过点 P 再次折叠纸片，使点 C 落在直线 PB′上，得点 C′和折痕 PQ，若 AQ=m，试用含有 t 的式子 表示 m； （Ⅲ）在（Ⅱ）的条件下，当点 C′恰好落在边 OA 上时，求点 P 的坐标（直接写出结果即可）． 5 AO OE OC OF = 5 2 2 5 5 5 5 2 5 2 5 12 【答案】解：（Ⅰ）根据题意，∠OBP=90°，OB=6。 在 Rt△OBP 中，由∠BOP=30°，BP=t，得 OP=2t。 ∵OP2=OB2+BP2，即（2t）2=62+t2，解得：t1= ，t2=－ （舍去）． ∴点 P 的坐标为（ ，6）。 （Ⅱ）∵△OB′P、△QC′P 分别是由△OBP、△QCP 折叠得到的， ∴△OB′P≌△OBP，△QC′P≌△QCP。 ∴∠OPB′=∠OPB，∠QPC′=∠QPC。 ∵∠OPB′+∠OPB+∠QPC′+∠QPC=180°，∴∠OPB+∠QPC=90°。 ∵∠BOP+∠OPB=90°，∴∠BOP=∠CPQ。 又∵∠OBP=∠C=90°，∴△OBP∽△PCQ。∴ 。 由题意设 BP=t，AQ=m，BC =11，AC=6，则 PC=11－t，CQ=6－m． ∴ 。∴ （0＜t＜11）。 （Ⅲ）点 P 的坐标为（ ，6）或（ ，6）。 【分析】（Ⅲ）首先过点 P 作 PE⊥OA 于 E，易证得△PC′E∽△C′QA，由勾股定理可求得 C′Q 的长，然后利用相似 三角形的对应边成比例与 ，即可求得 t 的值： 过点 P 作 PE⊥OA 于 E，∴∠PEA=∠QAC′=90°。 ∴∠PC′E+∠EPC′=90°。 ∵∠PC′E+∠QC′A=90°，∴∠EPC′=∠QC′A。 ∴△PC′E∽△C′QA。∴ 。 ∵PC′=PC=11－t，PE=OB=6，AQ=m，C′Q=CQ=6－m， ∴ 。 ∴ 。 ∵ ，即 ，∴ ，即 。 将 代入，并化简，得 。解得： 。 ∴点 P 的坐标为（ ，6）或（ ，6）。 2 3 2 3 2 3 OB BP PC CQ = 6 t 11 t 6 m =− − 21 11m t t 66 6 = − + 11 13 3 − 11+ 13 3 21 11m t t 66 6 = − + PE PC AC C Q ′=′ ′ 2 2AC C Q AQ 36 12m′ = ′ − = − 6 11 t 6 m36 12m −= −− 6 t 11 t 6 m =− − 6 11 t t 6 m −= − 6 6= t36 12m− 236 12m=t− 21 11m t t 66 6 = − + 23t 22 t 36=0− + 1 2 11 13 11+ 13t t3 3 −= =， 11 13 3 − 11+ 13 3 13 例 3.（2012 湖南岳阳 3 分）如图，△ABC 中，AB=AC，D 是 AB 上的一点，且 AD= AB，DF∥BC，E 为 BD 的中点．若 EF⊥AC，BC=6，则四边形 DBCF 的面积为　 ▲ 　． 【答案】15。 【分析】如图，过 D 点作 DG⊥AC，垂足为 G，过 A 点作 AH⊥BC，垂足为 H， ∵AB=AC，点 E 为 BD 的 中点，且 AD= AB， ∴设 BE=DE=x，则 AD=AF=4x。∵DG⊥AC，EF⊥AC， ∴DG∥EF，∴ ，即 ，解得 。 ∵DF∥BC，∴△ADF∽△ABC，∴ ，即 ，解得 DF=4。 又∵DF∥BC，∴∠DFG=∠C， ∴Rt△DFG∽Rt△ACH，∴ ，即 ，]解得 。 在 Rt△ABH 中，由勾股定理，得 。 ∴ 。 又∵△ADF∽△ABC，∴ ，∴ ∴ 。 例 4. （2011 山东淄博 4 分）如图，正方体的棱长为 3，点 M，N 分别在 CD，HE 上，CM= DM，HN=2NE， HC 与 NM 的延长线交于点 P，则 tan∠NPH 的值为 ▲ ． 【答案】 。 【考点】正方形的性质，相似三角形的判定和性质，锐角三角函数。 【分析】∵CM＝ DM，HN＝2NE，∴CM＝ CD，HN＝ HE＝ CD， 又∵△PCM∽△PHN，∴ ，即 PH＝2CH＝2CD。 ∴tan∠NPH＝ 。 2 3 2 3 AE DE=AF GF 5x x=4x GF 4GF= x5 DF AD=BC AB DF 4x=6 6x DF GF=AC HC 4 x4 5=6x 3 2 5x = 2 2 2 2 2 5AH= AB BH 36x 3 = 36 9=92 − = − × − ABC 1 1S BC AH 6 9 272 2∆ = ⋅ ⋅ = × × = 2 2 ADF ABC S DF 4 4 S BC 6 9 ∆ ∆    = = =       ADF 4S 27=129∆ = × ABC ADFDBCFS S S 27 12 15∆ ∆= − = − =四 形边 1 2 1 3 1 2 1 3 2 3 2 3 PC CM 1 PH HN 2 = = HN 1 PH 3 = 14 六、构造特殊四边形：通过构造平行四边形、矩形、菱形、正方形、梯形等特殊四边形，应用它们边、角、对 角线、中位线的性质，达到求证（解）的目的。 典型例题： 例 1. （2012 贵州遵义 3 分）如图，矩形 ABCD 中，E 是 AD 的中点，将△ABE 沿 BE 折叠后 得到△GBE，延长 BG 交 CD 于 F 点，若 CF=1，FD=2，则 BC 的长为【 】 A． B． C． D． 【答案】B。 【分析】过点 E 作 EM⊥BC 于 M，交 BF 于 N。 ∵四边形 ABCD 是矩形，∴∠A=∠ABC=90°，AD=BC， ∵∠EMB=90°，∴四边形 ABME 是矩形。∴AE=BM， 由折叠的性质得：AE=GE，∠EGN=∠A=90°，∴EG=BM。 ∵∠ENG=∠BNM，∴△ENG≌△BNM（AAS）。∴NG=NM。 ∵E 是 AD 的中点，CM=DE，∴AE=ED=BM=CM。 ∵EM∥CD，∴BN：NF=BM：CM。∴BN=NF。∴NM= CF= 。∴NG= 。 ∵BG=AB=CD=CF+DF=3，∴BN=BG﹣NG=3﹣ 。∴BF=2BN=5 ∴ 。故选 B。 例 2. （2012 四川德阳 3 分） 如图，点 D 是△ABC 的边 AB 的延长线上一点，点 F 是边 BC 上的一个动 点（不与点 B 重合）.以 BD、BF 为邻边作平行四边形 BDEF，又 AP BE（点 P、E 在直线 AB 的同侧），如果 ，那么△PBC 的面积与△ABC 面积之比为【 】 A. B. C. D. 【答案】D。 【分析】过点 P 作 PH∥BC 交 AB 于 H，连接 CH，PF，PE。 ∵AP BE，∴四边形 APEB 是平行四边形。∴PE AB。， ∵四边形 BDEF 是平行四边形，∴EF BD。 ∴EF∥AB。∴P，E，F 共线。 设 BD=a，∵ ，∴PE=AB=4a。∴PF =PE﹣EF=3a。 ∵PH∥BC，∴S△HBC=S△PBC。 ∵PF∥AB，∴四边形 BFPH 是平行四边形。∴BH=PF=3a。 ∵S△HBC：S△ABC=BH：AB=3a：4a=3：4，∴S△PBC：S△ABC=3：4。故选 D。 3 2 2 6 2 5 2 3 1 2 1 2 1 2 1 5 2 2 = 2 2 2 2BC BF CF 5 1 2 6= − = − = BD B1 4 A= 4 1 5 3 5 1 4 3 1BD AB4 = 15 例 3.（2012 安徽省 5 分）如图，P 是矩形 ABCD 内的任意一点，连接 PA、PB、PC、PD，得到△PAB、△PBC、△PCD、 △PDA，设它们的面积分别是 S1、S2、S3、S4，给出如下结论： ①S1+S2=S3+S4 ② S2+S4= S1+ S3 ③若 S3=2 S1，则 S4=2 S2 ④若 S1= S2，则 P 点在矩形的对角线上 其中正确的结论的序号是 ▲ （把所有正确结论的序号都填在横线上）. 【答案】②④。 【分析】如图，过点 P 分别作四个三角形的高， ∵△APD 以 AD 为底边，△PBC 以 BC 为底边， ∴此时两三角形的高的和为 AB，∴S1+S3= S 矩形 ABCD； 同理可得出 S2+S4= S 矩形 ABCD。 ∴②S2+S4= S1+ S3 正确，则①S1+S2=S3+S4 错误。 若 S3=2 S1，只能得出△APD 与△PBC 高度之比，S4 不一定等于 2S2；故 结论③错误。 如图，若 S1=S2，则 ×PF×AD= ×PE×AB， ∴△APD 与△PBA 高度之比为：PF：PE =AB：AD 。 ∵∠DAE=∠PEA=∠PFA=90°，∴四边形 AEPF 是矩形， ∴矩形 AEPF∽矩形 ABCD。连接 AC。∴PF：CD =PE ：BC=AP：AC，即 PF：CD =AF ：AD=AP：AC。 ∴△APF∽△ACD。∴∠PAF=∠CAD。∴点 A、P、C 共线。∴P 点在矩形的对角线上。 故结论④正确。综上所述，结论②和④正确。 例 4.（2012 广西贵港 8 分）如图，在□ABCD 中，延长 CD 到 E，使 DE＝CD，连接 BE 交 AD 于点 F，交 AC 于点 G。 （1）求证：AF＝DF； （2）若 BC＝2AB，DE＝1，∠ABC＝60°，求 FG 的长。 【答案】解：（1）证明：如图 1，连接 BD、AE， ∵四边形 ABCD 是平行四边形，∴AB∥CD，AB＝CD。 ∵DE＝CD，∴AB∥DE，AB＝DE。∴四边形 ABDE 是平行四边形。∴AF＝DF。 （2）如图 2，在 BC 上截取 BN＝AB＝1，连接 AN， ∵∠ABC＝60°，∴△ANB 是等边三角形。 ∴AN＝1＝BN，∠ANB＝∠BAN＝60°。 ∵BC＝2AB＝2，∴CN＝1＝AN。 1 2 1 2 1 2 1 2 16 ∴∠ACN＝∠CAN＝ 1 2×60°＝30°。 ∴∠BAC＝90°。 由勾股定理得：AC＝ 22－12＝ 3。 ∵四边形 ABCD 是平行四边形，∴AB∥CD。 ∴△AGB∽△CGE。∴ BG GE＝ AB CE＝ AG CG。∴ 1 1＋1＝ AG 3－AG，解 得 AG＝ 3 3 。 在△BGA 中，由勾股定理得：BG＝ 12＋( 3 3 )2＝ 2 3 3 。 ∵ BG GE＝ 1 2， ∴GE＝ 4 3 3 ，BE＝ 4 3 3 ＋ 2 3 3 ＝2 3。 ∵四边形 ABDE 是平行四边形，∴BF＝ 1 2BE＝ 3。∴FG＝ 3－ 2 3 3 ＝ 3 3 。 例 5.（2012 江苏常州 7 分）如图，在四边形 ABCD 中，AD∥BC，对角线 AC 的中点 为 O，过点 O 作 AC 的垂直平分线分别与 AD、BC 相交于点 E、F，连接 AF。 求证：AE=AF。 【答案】证明：连接 CE。 ∵AD∥BC，∴∠AEO=∠CFO，∠EAO=∠FCO，。 又∵AO=CO，∴△AEO≌△CFO（AAS）。 ∴AE=CF。∴四边形 AECF 是平行四边形。 又∵EF⊥AC，∴平行四边形 AECF 是菱形。 ∴AE=AF。 【考点】菱形的判定和性质，平行的性质，全等三角形的判定和性质。 例 6.（2012 海南省 11 分）如图（1），在矩形 ABCD 中，把∠B、∠D 分别翻折，使点 B、D 分别落在对角 线 BC 上的点 E、F 处，折痕分别为 CM、AN. （1）求证：△AND≌△CBM. （2）请连接 MF、NE，证明四边形 MFNE 是平行四边形，四边形 MFNE 是菱形吗？请说明理由？ （3）P、Q 是矩形的边 CD、AB 上的两点，连结 PQ、CQ、MN，如图（2）所示，若 PQ=CQ，PQ∥MN。且 AB=4，BC=3，求 PC 的长度. 17 【答案】（1）证明：∵四边形 ABCD 是矩形，∴∠D=∠B，AD=BC，AD∥BC。 ∴∠DAC=∠BCA。 又由翻折的性质，得∠DAN=∠NAF，∠ECM=∠BCM，∴∠DAN=∠BCM。 ∴△AND≌△CBM（ASA）。 （2）证明：∵△AND≌△CBM，∴DN=BM。 又由翻折的性质，得 DN=FN，BM=EM， ∴FN=EM。 又∠NFA=∠ACD＋∠CNF=∠BAC＋∠EMA=∠MEC， ∴FN∥EM。∴四边形 MFNE 是平行四边形。 四边形 MFNE 不是菱形，理由如下： 由翻折的性质，得∠CEM=∠B=900， ∴在△EMF 中，∠FEM＞∠EFM。 ∴FM＞EM。∴四边形 MFNE 不是菱形。 （3）解：∵AB=4，BC=3，∴AC=5。 设 DN=x，则由 S△ADC=S△AND＋S△NAC 得 3 x＋5 x=12，解得 x= ，即 DN=BM= 。 过点 N 作 NH⊥AB 于 H，则 HM=4－3=1。 在△NHM 中，NH=3，HM=1，由勾股定理，得 NM= 。 ∵PQ∥MN，DC∥AB，∴四边形 NMQP 是平行四边形。∴NP=MQ，PQ= NM= 。 又∵PQ=CQ，∴CQ= 。在△CBQ 中，CQ= ，CB=3，由勾股定理，得 BQ=1。 ∴NP=MQ= 。∴PC=4－ － =2。 【考点】翻折问题，翻折的性质，矩形的性质，平行的性质，全等三角形的判定和性质，平行四边形的判定和性质， 菱形的判定，勾股定理。 3 2 3 2 10 10 10 10 1 2 3 2 1 2 18 七、构造圆的特殊图形：通过构造圆的特殊图形，应用圆周角定理、垂径定理、切线与过切点的半（直）径的 关系、两圆相切公切线的性质、两圆相交公共弦的性质等，达到求证（解）的目的。 典型例题： 例 3.（2012 山东日照 4 分）如图，过 A、C 、D 三点的圆的圆心为 E，过 B、F、E 三点的圆的圆心为 D，如果 ∠A=63°，那么∠θ= ▲ ．[来︿源 【答案】180。 【分析】如图，连接 CE，DE， ∵过 A、C 、D 三点的圆的圆心为 E，过 B、F、E 三点的圆的圆心为 D， ∴AE=CE=DE=DB。∴∠A=∠ACE，∠ECD=∠CDE，∠DEB=∠DBE=∠θ。 ∵∠A=63°，∴∠AEC=1800－2×630=540。 又 ∵∠ECD=∠CDE=2∠θ ， ∴∠AEC=∠ ECD ＋ ∠DBE=3∠θ ， 即 3∠θ=540。∴∠θ=180。 19 例 4.（2012 湖北鄂州 3 分）如下图 OA=OB=OC 且∠ACB=30°，则∠AOB 的大小是【 】 A.40° B.50° C.60° D.70° 【答案】C。 【考点】圆周角定理。 【分析】∵OA=OB=OC，∴A、B、C 在以 O 为圆心 OA 为半径的圆上。 作⊙O。 ∵ ∠ACB 和∠AOB 是同弧 所对的圆周角和圆心角，且∠ACB=30°， ∴根据同弧所对的圆周角是圆心角的一半的性质，得∠AOB=60°。故选 C。 例 5.（2012 天津市 3 分）如图，已知正方形 ABCD 的边长为 1，以顶点 A、B 为圆心，1 为半径的两弧交于点 E，以顶点 C、D 为圆心，1 为半径的两弧交于点 F，则 EF 的长为 ▲ ． 【答案】 。 【考点】正方形的性质，全等三角形的判定和性质，勾股定理。 【分析】连接 AE，BE，DF，CF。 ∵以顶点 A、B 为圆心，1 为半径的两弧交于点 E，AB=1， ∴AB=AE=BE，∴△AEB 是等边三角形。 ∴边 AB 上的高线为： 。 同理：CD 边上的高线为： 。 延长 EF 交 AB 于 N，并反向延长 EF 交 DC 于 M，则 E、F、M，N 共线。 ∵AE=BE，∴点 E 在 AB 的垂直平分线上。 同理：点 F 在 DC 的垂直平分线上。 ∵四边形 ABCD 是正方形，∴AB∥DC。∴MN⊥AB，MN⊥DC。 由正方形的对称性质，知 EM=FN。 ∴EF＋2EM=AD=1，EF＋EM= ，解得 EF= 。 例 6.（2012 广西玉林、防城港 3 分）如图，矩形 OABC 内接于扇形 MON，当 CN=CO 时，∠NMB 的度数是 ▲ . 【答案】30°。 【分析】连接 OB，∵CN=CO，∴OB=ON=2OC。∵四边形 OABC 是矩形，∴∠BCO=90°。 ∴ 。∴∠BOC=60°。∴∠NMB= ∠BOC=30°。 AB 3 1− 3 2 3 2 3 2 3 1− OC 1cos BOC OB 2 ∠ = = 1 2 20 八、基本辅助线：基本辅助线包括连接两点的线段、平行线、垂直线、角平分线等，如连接直角三角形直角顶 点与斜边的中点构成斜边上的中线；过三角形一边的中点作另一边的平行线构成三角形的中位线；过三角形一顶点 作对边的垂直线构成直角三角形；连接圆上一点和直径的两端点构成直角三角形；等等。 典型例题： 例 2.（2012 广东佛山 6 分）如图，已知 AB=DC，DB=AC （1）求证：∠ABD=∠DCA，注：证明过程要求给出每一步结论成立的依据． （2）在（1）的证明过程中，需要作辅助线，它的意图是什么？ 【答案】证明：（1）连接 AD， 在△BAD 和△CDA 中， ∵ AB=CD （已知），DB=AC（已知）， AD=AD（公共边）， ∴△BAD≌△CDA（SSS）。 ∴∠ABD=∠DCA（全等三角形对应角相等）。 （2）作辅助线的意图是构造全等的三角形即两个三角形的公共边。 【考点】全等三角形的判定和性质。 例 3.（2012 贵州贵阳 3 分）如图，在 Rt△ABC 中，∠ACB=90°，AB 的垂直平分线 DE 交于 BC 的延长线于 F，若 ∠F=30°，DE=1，则 EF 的长是【 】 A．3 B．2 C． D．1 【答案】B。 3 21 【分析】连接 AF，∵DF 是 AB 的垂直平分线，∴AF=BF。 ∵FD⊥AB，∴∠AFD=∠BFD=30°，∠B=∠FAB=90°﹣30°=60°。 ∵∠ACB=90°，∴∠BAC=30°，∠FAC=60°﹣30°=30°。 ∵DE=1，∴AE=2DE=2。∵∠FAE=∠AFD=30°，∴EF=AE=2。故选 B。 例 5.（2012 四川宜宾 3 分）如图，在四边形 ABCD 中，DC∥AB，CB⊥AB，AB=AD，CD= AB， 点 E、F 分别为 AB．AD 的中点，则△AEF 与多边形 BCDFE 的面积之比为【 】 　 A． B． C． D． 【答案】C。 【分析】如图，连接 BD，过点 F 作 FG∥AB 交 BD 于点 G，连接 EG，CG。 ∵DC∥AB，CB⊥AB，AB=AD，CD= AB，点 E、F 分别为 AB．AD 的中点， ∴根据三角形中位线定理，得 AE=BE=AF=DF=DC=FG。 ∴图中的六个三角形面积相等。 ∴△AEF 与多边形 BCDFE 的面积之比为 。故选 C。 例 6.（2012 天津市 3 分）若一个正六边形的周长为 24，则该正六边形的面积为 ▲ ． 【答案】 。 【分析】根据题意画出图形，如图，连接 OB，OC，过 O 作 OM⊥BC 于 M， ∴∠BOC= ×360°=60°。 ∵OB=OC，∴△OBC 是等边三角形。∴∠OBC=60°。 ∵正六边形 ABCDEF 的周长为 24，∴BC=24÷6=4。 ∴OB=BC=4，∴BM=OB·sin∠OBC =4· 。 ∴ 。 例 7.（2012 福建厦门 10 分）已知 ABCD，对角线 AC 与 BD 相交于点 O，点 P 在边 AD 上，过点 P 分 别作 PE⊥AC、PF⊥BD，垂足分别为 E、F，PE＝PF． （1）如图，若 PE＝ 3，EO＝1，求∠EPF 的度数； （2）若点 P 是 AD 的中点，点 F 是 DO 的中点，BF ＝BC＋3 2－4，求 BC 的长． 【答案】解：（1）连接 PO , 1 2 1 7 1 6 1 5 1 4 1 2 1 5 24 3 1 6 3 =2 32 ABCDEF OBC 1 1S 6S 6 BC OM 6 4 2 3 24 32 2∆= = ⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ = 22 ∵ PE＝PF，PO＝PO，PE⊥AC、PF⊥BD， ∴ Rt△PEO≌Rt△PFO（HL）。 ∴∠EPO＝∠FPO。 在 Rt△PEO 中， tan∠EPO＝ EO PE＝ 3 ， ∴ ∠EPO＝30°。∴ ∠EPF＝60°。 （2）∵点 P 是 AD 的中点，∴ AP＝DP。 又∵ PE＝PF，∴ Rt△PEA≌Rt△PFD（HL）。 ∴∠OAD＝∠ODA。∴ OA＝OD。 ∴ AC＝2OA＝2OD＝BD。∴ ABCD 是矩形。 ∵ 点 P 是 AD 的中点，点 F 是 DO 的中点，∴ AO∥PF。 ∵ PF⊥BD，∴ AC⊥BD。∴ ABCD 是菱形。∴ ABCD 是正方形。 ∴ BD＝ 2BC。 ∵ BF＝ 3 4BD，∴BC＋3 2－4＝ 3 4BC，解得，BC＝4。 例 8.（2012 河北省 2 分）如图，CD 是⊙O 的直径，AB 是弦（不是直径），AB⊥CD 于点 E，则下列结 论正确的是【 】 A．AE＞BE B． C．∠D= ∠AEC D．△ADE∽△CBE 【答案】D。 【考点】垂径定理，圆周角定理，三角形外角性质，相似三角形的判定和性质。 【分析】∵CD 是⊙O 的直径，AB 是弦（不是直径），AB⊥CD于点 E， ∴根据垂径定理，得 AE=BE。故选项 A 错误。 如图，连接 AC，则根据同弧所对的圆周角相等的性质，得∠D=∠B， ∴BC=AC。 根据垂径定理，只有在 AB 是直径时才有 AC=AD ，而 AB 不是直径，∴AD≠AC 。∴ 。 ∴ 。故选项 B 错误。 如图，连接 AO，则根据同弧所对的圆周角是圆心角一半的性质，得∠D= ∠AOC。 ∵∠AEC 是△AOE 的外角，∴∠AEC＞∠AOC。∴∠D＜ ∠AEC。故选项 C 错误。  AD BC= 1 2  AD AC≠  AD BC≠ 1 2 1 2 23 ∵根据同弧所对的圆周角相等的性质，得∠D=∠B，∠DAE=∠BCE， ∴△ADE∽△CBE。故选项 D 正确。 例 9.（2012 宁夏区 6 分）在⊙O 中，直径 AB⊥CD 于点 E，连接 CO 并延长交 AD 于点 F,且 CF⊥AD. 求∠D 的度数. 【答案】解：连接 BD 。 ∵AB⊙O 是直径，∴BD ⊥AD。又∵CF⊥AD，∴BD∥CF。∴∠BDC=∠C。 又∵∠BDC= ∠BOC，∴∠C= ∠BOC。∵AB⊥CD，∴∠C=30°。∴∠ADC＝60°。 九、截取和延长变换：在一个平面几何图形内，延长或截取某一条线段，使条件和问题相对集中 ,达到化隐为 现的目的，常常使线段所在的三角形与平面内某一三角形成为全等三角形。证 明两条线段的和差，80%的情况都要用截长补短法。 典型例题： 例 1.（2012 江苏南京 2 分）如图，菱形纸片 ABCD 中，∠A=60 0，将纸片折 叠，点 A、D 分别落在 A’、D’处，且 A’D’经过 B，EF 为折痕，当 D’F CD 时， 的值为【 】 A. B. C. D. 【答案】A。 【分析】延长 DC 与 A′D′，交于点 M， ∵在菱形纸片 ABCD 中，∠A=60°， ∴∠DCB=∠A=60°，AB∥CD。 ∴∠D=180°-∠A=120°。 根据折叠的性质，可得∠A′D′F=∠D=120°， ∴∠FD′M=180°-∠A′D′F=60°。 ∵D′F⊥CD，∴∠D′FM=90°，∠M=90°-∠FD′M=30°。 ∵∠BCM=180°-∠BCD=120°，∴∠CBM=180°-∠BCM-∠M=30°。∴∠CBM=∠M。 ∴BC=CM。设 CF=x，D′F=DF=y， 则 BC=CM=CD=CF+DF=x+y。∴FM=CM+CF=2x+y， 在 Rt△D′FM 中，tan∠M=tan30°= ，∴ 。 。故选 A。 例 2.（2012 黑龙江牡丹江 3 分）如图，菱形 ABCD 中，AB=AC，点 E、F 分别为边 AB、BC 上的点， 1 2 1 2 ⊥ CF FD 3 1 2 − 3 6 2 3 1 6 − 3 1 8 + D F y 3 FM 2x y 3 ′ = =+ 3-1x y2 = CF x 3-1 FD y 2 = = 24 且 AE=BF，连接 CE、AF 交于点 H，连接 DH 交 AG 于点 O．则下列结论①△ABF≌△CAE，②∠AHC=1200，③AH+CH=DH，④AD 2=OD·DH 中，正确的是【 】． A. ①②④ B. ①②③ C. ②③④ D. ①②③④ 【答案】D。 【分析】∵菱形 ABCD 中，AB=AC，∴△ABC 是等边三角形。∴∠B=∠EAC=600。 又∵AE=BF，∴△ABF≌△CAE（SAS）。结论①正确。 ∵△ABF≌△CAE，∴∠BAF=∠ACE。 ∴∠AHC=1800－（∠ACE＋∠CAF）=1800－（∠BAF＋∠CAF）=1800－∠BAC=1800－600=1200。 结论②正确。 如图，在 HD 上截取 HG=AH。 ∵菱形 ABCD 中，AB=AC，∴△ADC 是等边三角形。 ∴∠ACD=∠ADC=∠CAD=600。 又∵∠AHC=1200，∴∠AHC＋∠ADC =1200＋600=1800。 ∴A，H，C，D 四点共圆。∴∠AHD=∠ACD =600。∴△AHG 是等边三角形。 ∴AH=AG，∠GAH=600。∴∠CAH=600－∠CAG=∠DAG。 又∵AC=AD，∴△CAH≌△DAG（SAS）。∴CH=DG。∴AH+CH= HG+ DG =DH。结论③正确。 ∵∠AHD =∠OAD=600，∠ADH=∠ODA，△ADH∽△ODA。∴ 。 ∴AD 2=OD·DH。结论④正确。 综上所述，正确的是①②③④。故选 D。 例 3.（2012 湖北天门、仙桃、潜江、江汉油田 3 分）如图，△ABC 为等边三角形，点 E 在 BA 的延长线上，点 D 在 BC 边上，且 ED=EC．若△ABC 的边长为 4，AE=2，则 BD 的长为【 】 A．2 B．3 C． D． 【答案】A。 【分析】延长 BC 至 F 点，使得 CF=BD， ∵ED=EC，∴∠EDB=∠ECF。∴△EBD≌△EFC（SAS）。∴∠B=∠F。 ∵△ABC 是等边三角形，∴∠B=∠ACB。∴∠ACB=∠F。 ∴AC∥EF。∴AE=CF=2。 ∴BD=AE=CF=2。故选 A。 AD HD OD AD = 3 3+1 25 例 4.（2012 山东枣庄 8 分）已知：如图，在四边形 ABCD 中，∠ABC＝90°，CD⊥AD，AD2＋CD2＝2AB2．（1）求证：AB＝ BC； （2）当 BE⊥AD 于 E 时，试证明：BE＝AE＋CD． 【答案】解：（1）证明：连接 AC。 ∵∠ABC＝90°，∴AB2＋BC2＝AC2。 ∵CD⊥AD，∴AD2＋CD2＝AC2。 ∵AD2＋CD2＝2AB2，∴AB2＋BC2＝2AB2。∴AB＝BC。 （2）证明：过 C 作 CF⊥BE 于 F。 ∵BE⊥AD，∴四边形 CDEF 是矩形。∴CD＝EF。 ∵∠ABE＋∠BAE＝90°，∠ABE＋∠CBF＝90°，∴∠BAE＝∠CBF。 又∵AB＝BC，∠BEA＝∠CFB，∴△BAE≌△CBF（AAS）。∴AE＝BF。 ∴BE＝BF＋EF ＝AE＋CD。 例 5.（2012 重庆市 10 分）已知：如图，在菱形 ABCD 中，F 为边 BC 的中点，DF 与 对角线 AC 交于点 M，过 M 作 ME⊥CD 于点 E，∠1=∠2． （1）若 CE=1，求 BC 的长； （2）求证：AM=DF+ME． 【答案】解：（1）∵四边形 ABCD 是菱形，∴AB∥CD。∴∠1=∠ACD。 ∵∠1=∠2，∴∠ACD=∠2。∴MC=MD。 ∵ME⊥CD，∴CD=2CE。∵CE=1，∴CD=2。∴BC=CD=2。 （2）证明：∵F 为边 BC 的中点，∴BF=CF= BC。∴CF=CE。 ∵在菱形 ABCD 中，AC 平分∠BCD，∴∠ACB=∠ACD 。 在△CEM 和△CFM 中，∵CE=CF，∠ACB=∠ACD，CM=CM， ∴△CEM≌△CFM（SAS），∴ME=MF。 延长 AB 交 DF 于点 G，∵AB∥CD，∴∠G=∠2。 ∵∠1=∠2，∴∠1=∠G。∴AM=MG。 在△CDF 和△BGF 中，∵∠G=∠2，∠BFG=∠CFD，BF=CF，∴△CDF≌△BGF（AAS）。∴GF=DF 。由图形可知，GM=GF+MF，∴AM=DF+ME。 十、平移变换：平移变换是几何变换中的基本变换之一，平移变换是使图形上的点沿同一方向平移同一距离得 1 2 26 到新的图形。平移变换前后的图形具有如下性质：（1）对应线段平行且相等； （2）对应角的两边平行且方向一致。 典型例题： 例 1. （2012 海南省 3 分）如图，∠APB=300，圆心在边 PB 上的⊙O 半径为 1cm， OP=3cm，若⊙O 沿 BP 方向移动，当⊙O 与 PA 相切时，圆心 O 移动的距离为 ▲ cm. 【答案】1 或 5。 【考点】直线与圆相切的性质，含 300 角直角三角形的性质。 【分析】如图，设⊙O 移动到⊙O1，⊙O2 位置时与 PA 相切。 当⊙O 移动到⊙O1 时，∠O1DP=900。 ∵∠APB=300，O1D=1，∴PO1=2。 ∵OP=3，∴OO1=1。 当⊙O 移动到⊙O2 时，∠O2EP=90 0。 ∵∠APB=300，O2D=1，∴∠O2PE=300，PO2=2。 ∵OP=3，∴OO1=5。 综上所述，当⊙O 与 PA 相切时，圆心 O 移动的距离为 1cm 或 5 cm。 例 2.（2012 江西南昌 3 分）如图，有 a、b、c 三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线【 】 　 A． a 户最长 B．b 户最长 C．c 户最长 D．三户一样长 【答案】D。 【考点】生活中的平移现象，平移的性质。 【分析】根据平移的性质，对于电线中横的和竖的线段分别采用割补法将线段向右进行 平移，便可直观观察到都是相等的。因此 a b c 三线长度相等。故选 D。 例 3. （2011 湖北黄冈、鄂州 3 分）如图：矩形 ABCD 的对角线 AC=10，BC=8，则图中五个小矩形的周 长之和为　 ▲ 　． 【答案】28。 【分析】由勾股定理，得 AB= ，将五个小矩形的所有上边平移至 AD，所有下边平移至 BC，所有左边平移至 AB，所有右边平移至 CD， 2 2 2 2AC BC 10 8 6− = − = 27 ∴五个小矩形的周长之和=2（AB+CD）=2×（6+8）=28。 例 4.（2012 广东珠海 9 分）如图，在等腰梯形 ABCD 中，ABDC，AB=3 ，DC= ，高 CE=2 ，对角线 AC、BD 交于 H，平行于线段 BD 的两条直线 MN、RQ 同时从 点 A 出发沿 AC 方向向点 C 匀速平移，分别交等腰梯形 ABCD 的边于 M、N 和 R、Q， 分别交对角线 AC 于 F、G；当直线 RQ 到达点 C 时，两直线同时停止移动．记等腰 梯形 ABCD 被直线 MN 扫过的图形面积为 S1、被直线 RQ 扫过的图形面积为 S2，若直 线 MN 平移的速度为 1 单位/秒，直线 RQ 平移的速度为 2 单位/秒，设两直线移动 的时间为 x 秒． （1）填空：∠AHB=　 　；AC=　 ； （2）若 S2=3S1，求 x； （3）设 S2=mS1，求 m 的变化范围． 【答案】解：（1）90°；4。 （2）直线移动有两种情况：0＜x＜ 及 ≤x≤2。 ①当 0＜x＜ 时，∵MN∥BD，∴△AMN∽△ARQ。 ∵直线 MN 平移的速度为 1 单位/秒，直线 RQ 平移的速度为 2 单位/秒， ∴△AMN 和△ARQ 的相似比为 1：2。 ∴ 。∴S2=4S1，与题设 S2=3S1 矛盾。 ∴当 0＜x＜ 时，不存在 x 使 S2=3S1。 ②当 ≤x≤2 时， ∵AB∥CD，∴△ABH∽△CDH。 ∴CH：AH=CD：AB=DH：BH=1：3。 ∴CH=DH= AC=1，AH═BH=4﹣1=3。 ∵CG=4﹣2x，AC⊥BD，∴S△BCD= ×4×1=2 ∵RQ∥BD，∴△CRQ∽△CDB。 ∴ 。 又 ， 2 2 2 3 2 3 2 3 2 2 2 1 S 2 4S 1  = =   3 2 3 2 1 4 1 2 ( )2 2 CRQ 4 2xS 2 =8 2 x1∆ − = ⋅ −   ABCD ABD 1 1 1 1S AB CD CE 3 2 2 2 2 8 S AB CE 3 2 2 2 62 2 2 2∆= + ⋅ = ⋅ + ⋅ = = ⋅ = ⋅ ⋅ =梯形 （ ） （ ） ， 28 ∵MN∥BD，∴△AMN∽△ADB。∴ ， ∴S1= x2，S2=8﹣8（2﹣x）2。 ∵S2=3S1，∴8﹣8（2﹣x）2=3· x2，解得：x1= （舍去），x2=2。 ∴x 的值为 2。 （3）由（2）得：当 0＜x＜ 时，m=4， 当 ≤x≤2 时，∵S2=mS1， ∴ 。 ∴m 是 的二次函数，当 ≤x≤2 时，即当 时，m 随 的增大而增大， ∴当 x= 时，m 最大，最大值为 4；当 x=2 时，m 最小，最小值为 3。 ∴m 的变化范围为：3≤m≤4。 【分析】（1）过点 C 作 CK∥BD 交 AB 的延长线于 K， ∵CD∥AB，∴四边形 DBKC 是平行四边形。 ∴BK=CD= ，CK=BD。 ∴AK=AB+BK= 。 ∵四边形 ABCD 是等腰梯形，∴BD=AC。 ∴AC=CK。∴AE=EK= AK=2 =CE。 ∵CE 是高，∴∠K=∠KCE=∠ACE=∠CAE=45°。∴∠ACK=90°。∴∠AHB=∠ACK=90° ∴AC=AK•cos45°= 。 （2）直线移动有两种情况：0＜x＜ 及 ≤x≤2；然后分别从这两种情况分析求解：当 0＜x＜ 时，易得 S2=4S1≠3S1；当 ≤x≤2 时，根据相似三角形的性质与直角三角形的面积的求解方法，可求得 △BCD 与△CRQ 的面积，继而可求得 S2 与 S1 的值，由 S2=3S1，即可求得 x 的值； 2 2 1 ABD S AF x S AH 9∆  = =   2 3 2 3 6 2 5 3< 3 2 3 2 ( )2 2 2 221 8 8 2 xS 36 48 1 2m= = + 12= 36 +42S x x 3xx3 − −  = − − − −   1 x 3 2 1 1 2 2 x 3 ≤ ≤ 1 x 3 2 2 3 2+ 2=4 2 1 2 2 24 2 42 × = 3 2 3 2 3 2 3 2 29 （3）由（2）可得当 0＜x＜ 时，m=4；当 ≤x≤2 时，可得 ，化为关于 的二次函数 ，利用二次函数的性 质求得 m 的变化范围。 十一、旋转变换：旋转变换是几何变换中的基本变换之一，通过旋转，改变位置后重 新组合，然后在新图形中分析有关图形间的关系，进而揭示条件与结论间的内在联系，找到证题途径。旋转变换的 性质（1）旋转不改变图形的大小与形状，只改变图形的性质，也就是旋转前后图形全等；（2）对应点与旋转中心所 连线段间的夹角为旋转角。 典型例题： 例 1. （2012 四川南充 3 分）如图，四边形 ABCD 中，∠BAD=∠BCD=900,AB=AD,若四边形 ABCD 的面积是 24cm2.则 AC 长是 ▲ cm. 【答案】4 。 【考点】等腰直角三角形的性质，旋转的性质，勾股定理。 【分析】如图，将△ADC 旋转至△ABE 处，则△AEC 的面 积和四边形 ABCD 的面积一样多为 24cm2，,这时三角形△AEC 为等腰直角三角形，作边 EC 上的高 AF，则 AF= EC=FC, ∴ S△AEC= AF·EC=AF2=24 。∴AF2=24。 ∴AC2=2AF2=48 AC=4 。 例 2. （2011 广西贵港 3 分）如图所示，在梯形 ABCD 中，AB∥CD，E 是 BC 的中点， EF⊥AD 于点 F， AD＝4，EF＝5，则梯形 ABCD 的面积是【 】 A．40 B．30 C．20 D．10 【答案】C。 【考点】旋转变换和性质。 【分析】根据旋转的概念，旋转不改变图形的大小与形状，也就是旋 转前后图形全等。如图，将四边形 ECDF 旋转到 EBGH 的位置，这 样梯形 ABCD 的面积就等于梯形 AFHG 的面积，且 HG＝FD，HG＋FA＝AD＝4，HF＝2 EF＝10。因此， 它们的面积就等于 。故选 C。 3 2 3 2 ( )2 2 21 8 8 2 xSm= 2S x3 − −= 1 x 21 2m= 36 +4x 3  − −   3 1 2 1 2 3 1 4 10=202 × × 30