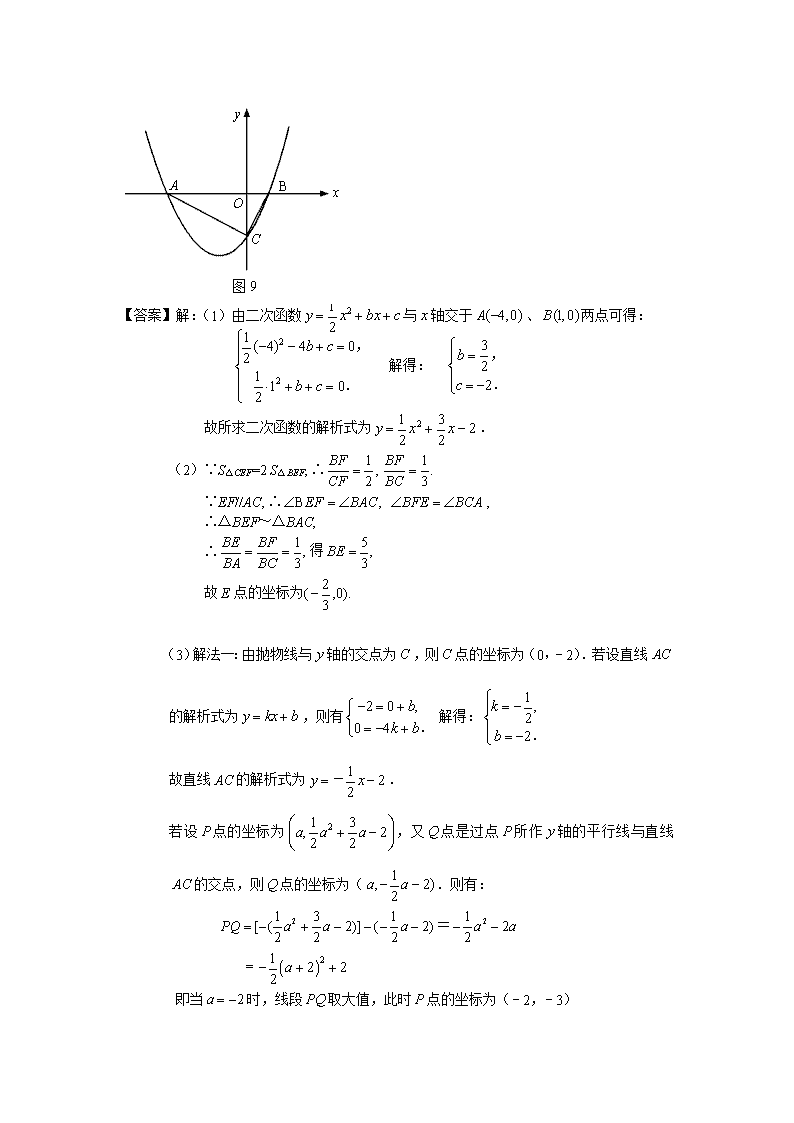2010中考数学分类汇编动态综合型问题2 27页

‎2010中考数学分类汇编 一、选择题 ‎1．（2010湖北鄂州）如图所示，四边形OABC为正方形，边长为6，点A、C分别在x轴，y轴的正半轴上， 点Ｄ在OA上，且Ｄ点的坐标为（2，0），P是OB上的一个动点，试求PD+PA和的最小值是（ ）‎ A．　　　B．　　C．4　　　D．6‎ ‎【答案】A ‎ ‎2．3．4．5．6．7．8．9．10．‎ ‎11．12．13．14．15．16．17．18．19．20．‎ ‎21．22．23．24．25．26．27．28．29．30．‎ 二、填空题 ‎1．2．3．4．5．6．7．8．9．10．‎ ‎11．12．13．14．15．16．17．18．19．20．‎ ‎21．22．23．24．25．26．27．28．29．30．‎ 三、解答题 ‎1．（2010广东中山）如图（1），（2）所示，矩形ABCD的边长AB=6，BC=4，点F在DC上，DF=2．动点M、N分别从点D、B同时出发，沿射线DA、线段BA向点A的方向运动（点M可运动到DA的延长线上），当动点N运动到点A时，M、N两点同时停止运动．连接FM、MN、FN，当F、N、M不在同一直线时，可得ΔFMN，过ΔFMN三边的中点作ΔPQW．设动点M、N的速度都是1个单位/秒，M、N运动的时间为x秒．试解答下列问题：‎ ‎（1）说明ΔFMN∽ΔQWP；‎ ‎（2）设0≤x≤4（即M从D到A运动的时间段）．试问x为何值时，ΔPQW为直角三角形？当x在何范围时，ΔPQW不为直角三角形？‎ ‎（3）问当x为何值时，线段MN最短？求此时MN的值．‎ ‎．‎ ‎【答案】解：（1）由题意可知P、W、Q分别是ΔFMN三边的中点，‎ ‎∴PW是ΔFMN的中位线，即PW∥MN ‎∴ΔFMN∽ΔQWP ‎（2）由题意可得 DM=BN=x，AN=6-x，AM=4-x，‎ 由勾股定理分别得 =，‎ ‎=+‎ ‎=+‎ ‎①当=+时，+=++‎ 解得 ‎ ‎②当=+时，+=++‎ 此方程无实数根 ‎③=+时，=+++‎ 解得 （不合题意，舍去），‎ 综上，当或时，ΔPQW为直角三角形；‎ 当0≤x＜或＜x＜4时，ΔPQW不为直角三角形 ‎（3）①当0≤x≤4，即M从D到A运动时，只有当x=4时，MN的值最小，等于2；‎ ‎②当4＜x≤6时，=+=+‎ ‎=‎ 当x=5时，取得最小值2，‎ ‎∴当x=5时，线段MN最短，MN=．‎ ‎2．（2010湖南常德）如图9, 已知抛物线与轴交于A (－4，0) 和B(1，0)两点，与轴交于C点．‎ ‎（1）求此抛物线的解析式；‎ ‎（2）设E是线段AB上的动点，作EF//AC交BC于F，连接CE，当△CEF的面积是△BEF面积的2倍时，求E点的坐标;‎ ‎（3）若P为抛物线上A、C两点间的一个动点，过P作轴的平行线，交AC于Q，当P点运动到什么位置时，线段PQ的值最大，并求此时P点的坐标．‎ x y O B C A 图9‎ ‎【答案】解：（1）由二次函数与轴交于、两点可得：‎ ‎　　　　　　　　　　解得：　‎ ‎　　　　　　故所求二次函数的解析式为． ‎ ‎（2）∵S△CEF=2 S△BEF, ∴ ‎ ‎ ∵EF//AC, ∴,‎ ‎ ∴△BEF～△BAC, ‎ ‎∴得 ‎ 故E点的坐标为(,0). ‎ ‎　　　（3）解法一：由抛物线与轴的交点为，则点的坐标为（0，－2）．若设直线的解析式为，则有　解得： ‎ 故直线的解析式为． ‎ 若设点的坐标为，又点是过点所作轴的平行线与直线的交点，则点的坐标为（．则有：‎ ‎　　　　　　　＝‎ ‎＝‎ 即当时，线段取大值，此时点的坐标为（－2，－3）‎ 解法二：延长交轴于点，则．要使线段最长，则只须△的面积取大值时即可. ‎ 设点坐标为（，则有: ‎ ‎　　　 ‎ ‎ 　 ＝‎ ‎　 ＝‎ ‎ ＝‎ ‎＝‎ ‎＝ ＝－‎ 即时，△的面积取大值，此时线段最长，则点坐标 为（－2，－3） ‎ ‎3．（2010湖北荆州）如图，直角梯形OABC的直角顶点O是坐标原点，边OA，OC分别在x轴、y轴的正半轴上，OA∥BC，D是BC上一点，BD=OA=，AB=3，∠OAB=45°，E、F分别是线段OA、AB上的两动点，且始终保持∠DEF=45°．‎ ‎（1）直接写出D点的坐标；‎ ‎（2）设OE=x，AF=y，试确定y与x之间的函数关系；‎ ‎（3）当△AEF是等腰三角形时，将△AEF沿EF折叠，得到△，求△与五边形OEFBC重叠部分的面积．‎ ‎【答案】解：（1）D点的坐标是.‎ ‎（2）连结OD,如图（1），‎ 由结论（1）知：D在∠COA的平分线上，则 ‎∠DOE=∠COD=45°,又在梯形DOAB中，∠BAO=45°,∴OD=AB=3‎ 由三角形外角定理得：∠1=∠DEA-45°,又∠2=∠DEA-45°‎ ‎∴∠1=∠2, ∴△ODE∽△AEF ‎∴，即：‎ ‎∴y与x的解析式为：‎ ‎（3）当△AEF为等腰三角形时，存在EF=AF或EF=AE或AF=AE共3种情况.‎ ① 当EF=AF时，如图（2）.‎ ‎∠FAE=∠FEA=∠DEF=45°,‎ ‎∴△AEF为等腰直角三角形.D在A’E上（A’E⊥OA）,‎ B在A’F上（A’F⊥EF）‎ ‎∴△A’EF与五边形OEFBC重叠的面积为 四边形EFBD的面积.‎ ‎∵‎ ‎∴‎ ‎∴‎ ‎∴（也可用）‎ ‎ ‎ ‎②当EF=AE时，如图（3），‎ 此时△A’EF与五边形OEFBC重叠部分面积为△A’EF面积.‎ ‎∠DEF=∠EFA=45°， DE∥AB ， 又DB∥EA ‎∴四边形DEAB是平行四边形 ‎∴AE=DB=‎ ‎∴‎ ‎③当AF=AE时，如图（4），四边形AEA’F为菱形且△A’EF在五边形OEFBC内.‎ ‎ ∴此时△A’EF与五边形OEFBC重叠部分面积为△A’EF面积.‎ ‎ ‎ 由（2）知△ODE∽△AEF,则OD=OE=3‎ ‎ ∴AE=AF=OA-OE=‎ ‎ 过F作FH⊥AE于H,则 ‎∴‎ 综上所述，△A’EF与五边形OEFBC重叠部分的面积为或1或 ‎4．（2010湖北鄂州）如图，在直角坐标系中，A（-1，0），B（0，2），一动点P沿过B点且垂直于AB的射线BM运动，P点的运动速度为每秒1个单位长度，射线BM与x轴交与点C．‎ ‎（1）求点C的坐标．‎ ‎（2）求过点A、B、C三点的抛物线的解析式．‎ ‎（3）若P点开始运动时，Q点也同时从C出发，以P点相同的速度沿x轴负方向向点A运动，t秒后，以P、Q、C为顶点的三角形为等腰三角形．（点P到点C时停止运动，点Q也同时停止运动）求t的值．‎ ‎（4）在（2）（3）的条件下，当CQ=CP时，求直线OP与抛物线的交点坐标．‎ ‎【答案】‎ ‎（1）点C的坐标是（4，0）；‎ ‎（2）设过点A、B、C三点的抛物线的解析式为y=ax2+bx+c（a≠0），将点A、B、C三点的坐标代入得：‎ 解得，∴抛物线的解析式是：y= x2+x+2．‎ ‎（3）设P、Q的运动时间为t秒，则BP=t，CQ=t．以P、Q、C为顶点的三角形为等腰三角形，可分三种情况讨论．‎ ‎①若CQ=PC，如图所示，则PC= CQ=BP=t．∴有2t=BC=，∴t=．‎ ‎②若PQ=QC，如图所示，过点Q作DQ⊥BC交CB于点D，则有CD=PD．由△ABC∽△QDC，可得出PD=CD=，∴，解得t=．‎ ‎③若PQ=PC，如图所示，过点P作PE⊥AC交AC于点E，则EC=QE=PC，∴t=（-t），解得t=．‎ ‎（4）当CQ=PC时，由（3）知t=，∴点P的坐标是（2，1），∴直线OP的解析式是：y=x，因而有x =x2+x+2，即x2-2x-4=0，解得x=1±，∴直线OP与抛物线的交点坐标为（1+，）和（1-，）．‎ ‎5．（2010湖北省咸宁）如图，直角梯形ABCD中，AB∥DC，，，．动点M以每秒1个单位长的速度，从点A沿线段AB向点B 运动；同时点P以相同的速度，从点C沿折线C-D-A向点A运动．当点M到达点B时，两点同时停止运动．过点M作直线l∥AD，与线段CD的交点为E，与折线A-C-B的交点为Q．点M运动的时间为t（秒）．‎ ‎（1）当时，求线段的长；‎ ‎（2）当0＜t＜2时，如果以C、P、Q为顶点的三角形为直角三角形，求t的值；‎ ‎（3）当t＞2时，连接PQ交线段AC于点R．请探究是否为定值，若是，试求这个定值；若不是，请说明理由．‎ A B C D ‎（备用图1）‎ A B C D ‎（备用图2）‎ Q A B C D l M P ‎（第24题）‎ E ‎【答案】解：（1）过点C作于F，则四边形AFCD为矩形．‎ Q A B C D l M P ‎（第24题）‎ E F ‎∴，．‎ 此时，Rt△AQM∽Rt△ACF．……2分 ‎∴．‎ 即，∴．‎ ‎（2）∵为锐角，故有两种情况：‎ ‎①当时，点P与点E重合．‎ 此时，即，∴．‎ A B C D ‎（备用图1）‎ Q P E l M ‎②当时，如备用图1，‎ 此时Rt△PEQ∽Rt△QMA，∴．‎ 由（1）知，，‎ 而，‎ ‎∴． ∴．‎ 综上所述，或．‎ ‎（3）为定值．‎ 当＞2时，如备用图2，‎ A B C D ‎（备用图2）‎ M Q R F P ‎．‎ 由（1）得，．‎ ‎∴． ∴．‎ ‎∴． ∴．‎ ‎∴四边形AMQP为矩形． ∴∥．‎ ‎∴△CRQ∽△CAB．‎ ‎∴．‎ ‎6．（2010江苏扬州）在△ABC中，∠C＝90°，AC＝3，BC＝4，CD是斜边AB上的高，点E在斜边AB上，过点E作直线与△ABC的直角边相交于点F，设AE＝x，△AEF的面积为y．‎ ‎（1）求线段AD的长；‎ ‎（2）若EF⊥AB，当点E在线段AB上移动时，‎ ‎①求y与x的函数关系式（写出自变量x的取值范围）‎ ‎②当x取何值时，y有最大值？并求其最大值；‎ ‎（3）若F在直角边AC上（点F与A、C两点均不重合），点E在斜边AB上移动，试问：是否存在直线EF将△ABC的周长和面积同时平分？若存在直线EF，求出x的值；若不存在直线EF，请说明理由．‎ A B C D A B C D 备用图 ‎【答案】解：（1）∵AC=3，BC=4‎ ‎∴AB=5‎ ‎∵AC·BC=AB·CD，‎ ‎∴CD=，AD=‎ ‎ （2）①当0＜x≤时 ‎ ∵EF∥CD ‎∴△AEF∽△ADC ‎∴‎ 即EF=x ‎∴y=·x·x=‎ ‎ 当＜x≤5时 ‎ 易得△BEF∽△BDC，同理可求EF=（5—x）‎ ‎ ∴y=·x·（5—x）=≤‎ ‎ ‎ ‎ ‎ ‎②当0＜x≤时，y随x的增大而增大.‎ y=≤,即当x=时，y最大值为 ‎ 当＜x≤5时，‎ ‎ ∵‎ ‎ ∴当时，y的最大值为 ‎ ∵＜‎ ‎ ∴当时，y的最大值为 ‎（3）假设存在 ‎ 当0＜x≤5时，AF=6—x ‎ ∴0＜6—x＜3‎ ‎ ∴3＜x＜6‎ ‎ ∴3＜x≤5‎ ‎ 作FG⊥AB与点G ‎ 由△AFG∽△ACD可得 ‎ ∴，即FG=‎ ‎ ∴x·=‎ ‎ ∴=3，即2x2-12x+5=0‎ ‎ 解之得x1=，x2=‎ ‎ ∵3＜x1≤5‎ ‎ ∴x1=符合题意 ‎ ∵x2=＜3‎ ‎ ∴x2不合题意，应舍去 ‎ ∴存在这样的直线EF，此时，x=‎ ‎7．（2010北京）在平面直角坐标系xOy中，抛物线与x轴的交点分别为原点O和点A，点B（2，n）在这条抛物线上．‎ ‎（1）求B点的坐标；‎ ‎（2）点P在线段OA上，从O点出发向A点运动，过P点作x轴的垂线，与直线OB交与点E，延长PE到点D，使得ED=PE，以PD为斜边，在PD右侧做等等腰直角三角形PCD（当P点运动时，C点、D点也随之运动）．‎ ‎① 当等腰直角三角形PCD的顶点C落在此抛物线上时，求OP的长；‎ ‎－1‎ y x O ‎（第24题）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎－2‎ ‎－4‎ ‎－3‎ ‎3‎ ‎－1‎ ‎－2‎ ‎－3‎ ‎－4‎ ‎4‎ ‎1‎ ‎2‎ ‎② 若P点从O点出发向A点作匀速运动，速度为每秒1个单位，同时线段OA上另一个点Q从A点出发向O点作匀速运动，速度为每秒2个单位（当Q点到达O点时停止运动，P点也同时停止运动）．过Q点做x轴的垂线，与直线AB交与点F，延长QF到点M，使得FM=QF，以QM为斜边，在QM的左侧作等腰直角三角形QMN（当Q点运动时，M点、N点也随之运动）．若P点运动到t秒时，两个等腰直角三角形分别有一条边恰好落在同一条直线上，求此刻t的值．‎ ‎【答案】解：（1）∵抛物线经过原点，‎ ‎∴m2—‎3m+2=0.‎ 解的m1=1，m2=2.‎ 由题意知m≠1.‎ ‎∴m=2，‎ ‎∴抛物线的解析式为 ‎∵点B（2，n）在抛物线，‎ n=4.‎ ‎∴B点的坐标为（2，4）‎ ‎（2）①设直线OB的解析式为y=k1x 求得直线OB的解析式y=2x ‎∵A点是抛物线与x轴的一个交点，‎ 可求得A点的坐标为（10，0），‎ 设P点的坐标为（a，0），则E点的坐标为（a，‎2a）．‎ 根据题意做等腰直角三角形PCD，如图1. ‎ 可求得点C的坐标为（‎3a，‎2a），‎ 有C点在抛物线上，‎ 得‎2a=－x（‎3a）2+x‎3a.‎ 即a2— a=0‎ 解得 a1=，a2=0（舍去）‎ ‎∴OP= ‎ ‎②依题意作等腰直角三角形QMN.‎ 设直线AB的解析式y=k2x+b 由点A(10 ，0)，点B（2，4），求得直线AB的解析式为y=－x+5‎ 当P点运动到t秒时，两个等腰直角三角形分别有一条边恰好落在同一条直线上，有以下三种情况：‎ 第一种情况：CD与NQ在同一条直线上，如图2所示，‎ 可证△DPQ为等腰直角三角形．此时QP、OP、AQ的长可依次表示为t 、4t、 2t个单位．‎ ‎∴PQ = DP = 4t ‎∴t+4t+2t=10‎ ‎∴t=‎ 第二种情况：PC与MN在同一条直线上，如图3所示．可证△PQM为等腰直角三角形．‎ 此时OP、AQ的长依次表示为t、2t个单位，‎ ‎∴OQ = 10 － 2t ‎∵F点在直线AB上 ‎∴FQ=t ‎∵MQ=2t ‎∴PQ=MQ=CQ=2t ‎∴t+2t+2t=10‎ ‎∴t=2.‎ 第三种情况：点P、Q重合时，PD、QM在同一条直线上，如图4所示，此时OP、AQ的长依次表示为t、2t个单位．‎ ‎∴t+2t=10‎ ‎∴t=‎ 综上，符合题意的值分别为，2，．‎ ‎8．（2010云南红河哈尼族彝族自治州）如图9，在直角坐标系xoy中，O是坐标原点，点A在x正半轴上，OA=cm，点B在y轴的正半轴上，OB=12cm，动点P从点O开始沿OA以cm/s的速度向点A移动，动点Q从点A开始沿AB以4cm/s的速度向点B移动，动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动，移动时间为t（0＜t＜6）s.‎ ‎（1）求∠OAB的度数.‎ ‎（2）以OB为直径的⊙O‘与AB交于点M，当t为何值时，PM与⊙O‘相切？‎ ‎（3）写出△PQR的面积S随动点移动时间t的函数关系式，并求s的最小值及相应的t值.‎ ‎（4）是否存在△APQ为等腰三角形，若存在，求出相应的t值，若不存在请说明理由.‎ ‎【答案】解：（1）在Rt△AOB中：‎ tan∠OAB=‎ ‎∴∠OAB=30°‎ ‎（2）如图10，连接O‘P，O‘M. 当PM与⊙O‘相切时，有∠PM O‘=∠PO O‘=90°，‎ ‎ △PM O‘≌△PO O‘‎ 由（1）知∠OBA=60°‎ ‎∵O‘M= O‘B ‎∴△O‘BM是等边三角形 ‎∴∠B O‘M=60°‎ 可得∠O O‘P=∠M O‘P=60°‎ ‎∴OP= O O‘·tan∠O O‘P ‎ =6×tan60°=‎ 又∵OP=t ‎∴t=，t=3‎ 即：t=3时，PM与⊙O‘相切.‎ ‎（3）如图9，过点Q作QE⊥x于点E ‎ ∵∠BAO=30°，AQ=4t ‎ ∴QE=AQ=2t ‎ AE=AQ·cos∠OAB=4t×‎ ‎∴OE=OA-AE=-t ‎ ∴Q点的坐标为（-t，2t）‎ ‎ S△PQR= S△OAB -S△OPR -S△APQ -S△BRQ ‎ =‎ ‎ =‎ ‎ = （）‎ ‎ 当t=3时，S△PQR最小=‎ ‎ （4）分三种情况：如图11.‎ 当AP=AQ1=4t时，‎ ‎∵OP+AP=‎ ‎∴t+4t=‎ ‎∴t=‎ 或化简为t=-18‎ 当PQ2=AQ2=4t时 ‎ 过Q2点作Q2D⊥x轴于点D，‎ ‎∴PA=2AD=2A Q2·cosA=t 即t+t =‎ ‎∴t=2‎ 当PA=PQ3时，过点P作PH⊥AB于点H ‎ AH=PA·cos30°=（-t）·=18-3t AQ3=2AH=36-6t 得36-6t=4t，‎ ‎∴t=3.6‎ ‎ 综上所述，当t=2，t=3.6，t=-18时，△APQ是等腰三角形.‎ ‎9．（2010云南楚雄）已知：如图，⊙与轴交于C、D两点，圆心的坐标为（1，0），⊙的半径为，过点C作⊙的切线交于点B（－4，0）．‎ ‎（1）求切线BC的解析式；‎ ‎（2）若点P是第一象限内⊙上一点，过点P作⊙A的切线与直线BC相交于点G，且∠CGP＝120°，求点的坐标；‎ ‎（3）向左移动⊙（圆心始终保持在上），与直线BC交于E、F，在移动过程中是否存在点，使得△AEF是直角三角形？若存在，求出点 的坐标，若不存在，请说明理由．‎ ‎【答案】解：（1）连接，∵是⊙A的切线，∴．‎ ‎∴．‎ ‎∵，∴，∴．‎ ‎∴△∽△，∴．‎ 即，∴．∴点坐标是（0，2）．‎ 设直线的解析式为，∵该直线经过点B（－4，0）与点（0，2），‎ ‎∴ 解得 ‎ ‎ ∴该直线解析式为．‎ ‎（2）连接，过点作．‎ 由切线长定理知 ‎．‎ 在中，∵，‎ ‎∴．‎ 在中，由勾股定理得 ‎ ‎．‎ ‎∴ ．‎ 又∵．‎ ‎∴∽，∴，‎ ‎∴．‎ 则是点的纵坐标，‎ ‎∴，解得．‎ ‎∴点的坐标．‎ ‎ (3)如图示，‎ 当在点的右侧时 ‎ ∵、在⊙上，∴．‎ 若△是直角三角形，则，且为等腰直角三角形．‎ 过点作，在中由三角函数可知 ‎．‎ 又∵∽ ，‎ ‎∴ ，‎ ‎∴．‎ ‎∴，‎ ‎∴点 坐标是．‎ 当在点的左侧时：同理可求点 坐标是．‎ ‎10．（2010四川乐山）如图(13.1)，抛物线y＝x2+bx+c与x轴交于A，B两点，与y轴交于点C(0，2)，连接AC，若tan∠OAC＝2．‎ ‎(1)求抛物线对应的二次函数的解析式；‎ ‎(2)在抛物线的对称轴l上是否存在点P，使∠APC＝90°，若存在，求出点P的坐标；若不存在，请说明理由；‎ ‎(3)如图(13.2)所示，连接BC，M是线段BC上(不与B、C重合)的一个动点，过点M作直线l′∥l，交抛物线于点N，连接CN、BN，设点M的横坐标为t．当t为何值时，△BCN的面积最大？最大面积为多少？‎ ‎【答案】解：（1）∵抛物线y=x2＋bx＋c过点C(0,2). ∴x=2‎ 又∵tan∠OAC==2, ∴OA=1,即A(1,0).‎ 又∵点A在抛物线y=x2＋bx＋2上. ∴0=12＋b×1＋2,b=－3‎ ‎∴抛物线对应的二次函数的解析式为y=x2－3x＋2‎ ‎（2）存在 过点C作对称轴l的垂线,垂足为D,如图所示,‎ ‎∴x=－.∴AE=OE-OA=-1=,∵∠APC=90°,‎ ‎∴tan∠PAE= tan∠CPD∴,即，解得PE=或PE=，‎ ‎∴点P的坐标为（，）或（，）。（备注：可以用勾股定理或相似解答）‎ ‎（3）如图，易得直线BC的解析式为：y=-x＋2，‎ ‎∵点M是直线l′和线段BC的交点，∴M点的坐标为（t，-t+2）(0＜t＜2)‎ ‎∴MN=-t+2-(t2－3t＋2)=- t2＋2t ‎∴S△BCM= S△MNC+S△MNB=MN▪t+MN▪(2-t)‎ ‎=MN▪(t+2-t)=MN=- t2＋2t(0＜t＜2),‎ ‎∴S△BCN=- t2＋2t=-(t-1)2+1‎ ‎∴当t=1时，S△BCN的最大值为1。‎ ‎11．（2010黑龙江哈尔滨）如图，在平面直角坐标系中，点O是坐标原点，四边形AOCB是梯形，AB∥OC，点A的坐标为（0，8），点C的坐标为（10，0），OB＝OC．‎ ‎ （1）求点B的坐标；‎ ‎ （2）点P从C点出发，沿线段CO以5个单位/秒的速度向终点O匀速运动，过点P作PH⊥OB，垂足为H，设△HBP的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（直接写出自变量t的取值范围）；‎ ‎ （3）在（2）的条件下，过点P作PM∥CB交线段AB于点M，过点M作MR⊥OC，垂足为R，线段MR分别交直线PH、OB于点E、G，点F为线段PM的中点，连接EF，当t为何值时，？‎ ‎ 【答案】解：（1）如图1，过点B作BN⊥OC，垂中为N 由题意知OB=OC=10，BN=OA=8‎ ‎…………1分 ∴B（6，8） ‎ ‎ （2）如图1，‎ ‎∽‎ ‎ ‎ ‎ ‎ ‎ （3）①当点G在点E上方时，‎ 如图2，过点B作，垂足为 ‎ ∴四边形BMPC是平行四边形 ‎ ‎ ‎∵PM∥CB ∴∠OPD=∠OCB ∠ODP=∠OBC ‎∴∠OPD=∠ODP ∵∠OPD+∠RMP=90° ∠ODP+∠DPH=90°‎ ‎∴∠RMP=∠DPH ∴EM=EF ‎ ‎∵点F为PM的中点 ∴EF⊥PM ‎∵∠EMF=∠PMR ∠EFM=∠PRM=90° ∴△MEF∽△MPR ‎∵AB//OC ∴∠MBG=∠BON′ 又∵∠GMB=∠ON′B=90°‎ ‎∴△MGB∽△NB′O ‎ ‎ ‎ ‎②当点G在点E下方时 如图3 同理可得 MG=ME+EG=5+2=7‎ ‎ ‎ ‎12．（2010江苏徐州）如图①，梯形ABCD中，∠C=90°．动点E、F同时从点B出发，点E沿折线 BA—AD—DC运动到点C时停止运动，点F沿BC运动到点C时停止运动，它们运动时的速度都是‎1 cm/s．设E、F出发t s时，△EBF的面积为y cm2．已知y与t的函数图象如图②所示，其中曲线OM为抛物线的一部分，MN、NP为线段．请根据图中的信息，解答下列问题：‎ ‎ (1)梯形上底的长AD=_____cm，梯形ABCD的面积_____cm2；‎ ‎ (2)当点E在BA、DC上运动时，分别求出y与t的函数关系式(注明自变量的取值范围)；‎ ‎ (3)当t为何值时，△EBF与梯形ABCD的面积之比为1：2.‎ ‎【答案】‎ ‎13．14．（2010 山东东营） 如图，在锐角三角形ABC中，，△ABC的面积为48，D，E分别是边AB，AC上的两个动点（D不与，重合），且保持DE∥BC，以DE为边，在点的异侧作正方形DEFG.‎ ‎（1）当正方形DEFG的边GF在BC上时，求正方形DEFG的边长；‎ B ‎（第24题图）‎ A D E F G C B ‎（备用图（1））‎ A C B ‎（备用图（2））‎ A C ‎（2）设DE = x，△ABC与正方形DEFG重叠部分的面积为，试求关于的函数关系式，写出x的取值范围，并求出y的最大值.‎ ‎【答案】解：（1）当正方形DEFG的边GF在BC上时，如图 ‎（1），过点A作BC边上的高AM，交DE于N，垂足为M.‎ B ‎（第24题图(1)）‎ A D E F G C M N ‎∵S△ABC=48，BC=12，∴AM=8. ‎ ‎∵DE∥BC，△ADE∽△ABC, ………1分 ‎∴，‎ 而AN=AM－MN=AM－DE，∴. ……………………2分 解之得.‎ ‎∴当正方形DEFG的边GF在BC上时，正方形DEFG的边长为4.8.…3分 B ‎（第24题图（2））‎ A D E F G C ‎（2）分两种情况：‎ ‎①当正方形DEFG在△ABC的内部时，如图（2），△ABC 与正方形DEFG重叠部分的面积为正方形DEFG的面积，‎ ‎∵DE=x，∴，此时x的范围是≤4.8…4分 ‎②当正方形DEFG的一部分在△ABC的外部时，‎ 如图（2），设DG与BC交于点Q，EF与BC交于点P，‎ M B ‎（第24题图(3)）‎ A D E F G C N P Q ‎△ABC的高AM交DE于N，‎ ‎∵DE=x，DE∥BC，∴△ADE∽△ABC, …………5分 即，而AN=AM－MN=AM－EP, ‎ ‎∴，解得.………6分 所以, 即.………7分 由题意，x>4.8，x<12,所以.‎ 因此△ABC与正方形DEFG重叠部分的面积为 ‎(0< x≤4.8)‎ ‎ ……………………………………8分 当≤4.8时，△ABC与正方形DEFG重叠部分的面积的最大值为4.82=23.04‎ 当时，因为，所以当时，‎ ‎△ABC与正方形DEFG重叠部分的面积的最大值为.‎ 因为24>23.04，‎ 所以△ABC与正方形DEFG重叠部分的面积的最大值为24. …………………10分15．（2010广东东莞）如图（1），（2）所示，矩形ABCD的边长AB＝6，BC＝4，点F在DC上，DF＝2．动点M、N分别从点D、B同时出发，沿射线DA、线段BA向点A的方向运动（点M可运动到DA的延长线上），当动点N运动到点A时，M、N两点同时停止运动．连接FM、MN、FN，当F、N、M不在同一直线时，可得△FMN，过△FMN三边的中点作△PQW．设动点M、N的速度都是1个单位／秒，M、N运动的时间为x秒．试解答下列问题：‎ ‎⑴说明△FMN ∽ △QWP；‎ ‎⑵设0≤≤4（即M从D到A运动的时间段）．试问为何值时，△PQW为直角三角形？当在何范围时，△PQW不为直角三角形？‎ ‎⑶问当为何值时，线段MN最短？求此时MN的值．‎ ‎【答案】⑴∵P、Q、W分别为△FMN三边的中点 ‎∴PQ∥FN，PW∥MN ‎∴∠MNF＝∠PQM＝∠QPW 同理：∠NFM＝∠PQW ‎∴△FMN ∽ △QWP ‎⑵‎ 由⑴得△FMN ∽ △QWP，所以△FMN为直角三角形时，△QWP也为直角三角形．如图，过点N作NECD于E，根据题意，得DM＝BM＝，∴AM＝4－，AN＝DE＝6－‎ ‎∵DF＝2，∴EF＝4－‎ ‎∴MF2＝22＋x2＝x2＋4，MN2＝（4－x）2＋（6－x）2＝2x2－20x＋52，NF2＝（4－x）2＋42＝x2－8x＋32,‎ ① 如果∠MNF＝90°，则有2x2－20x＋52＋x2－8x＋32＝x2＋4，解得x1＝4，x2＝10（舍去）；‎ ‎②如果∠NMF＝90°，则有2x2－20x＋52＋x2＋4＝x2－8x＋32，化简，得：x2－6x＋12＝0，△＝－12＜0，方程无实数根；‎ ‎③如果∠MFN＝90°，则有2x2－20x＋52＝x2＋4＋x2－8x＋32，解得x＝．‎ ‎∴当为4或时，△PQW为直角三角形，当0≤＜或＜＜4时，△PQW不为直角三角形 ‎⑶∵点M在射线DA上，点N在线段AB上，且AB⊥AD，∴当M点运动到与A点重合时，NM⊥AD，根据垂线段最短原理，此时线段MN最短，DM＝4，则BN＝4．‎ ‎∴当＝4时，线段MN最短，MN＝２．‎ ‎16．（2010湖北襄樊）如图7，四边形ABCD是平行四边形，AB=4，OB=2，抛物线过A、B、C三点，与x轴交于另一点D．一动点P以每秒1个单位长度的速度从B点出发沿BA向点A运动，运动到点A停止，同时一动点Q从点D出发，以每秒3个单位长度的速度沿DC向点C运动，与点P同时停止．‎ ‎ （1）求抛物线的解析式；‎ ‎ （2）若抛物线的对称轴与AB交于点E，与x轴交于点F，当点P运动时间t为何值时，四边形POQE是等腰梯形？‎ ‎ （3）当t为何值时，以P、B、O为顶点的三角形与以点Q、B、O为顶点的三角形相似？‎ 图7‎ ‎ ‎ ‎【答案】解：（1）∵四边形ABCD是平行四边形，‎ ‎∴OC=AB=4．‎ ‎∴A（4，2），B（0，2），C（－4，0）．‎ ‎∵抛物线y=ax2+bx+c过点B，∴c=2．‎ 由题意，有 解得 ‎∴所求抛物线的解析式为．‎ ‎（2）将抛物线的解析式配方，得．‎ ‎∴抛物线的对称轴为x=2．‎ ‎∴D（8，0），E（2，2），F（2，0）．‎ 欲使四边形POQE为等腰梯形，则有OP=QE．即BP=FQ．‎ ‎∴t=6－3t，即t=．‎ ‎ （3）欲使以P、B、O为顶点的三角形与以点Q、B、O为顶点的三角形相似，‎ ‎∵∠PBO=∠BOQ=90°，∴有或，‎ 即PB=OQ或OB2=PB·QO．‎ ‎①若P、Q在y轴的同侧．当PB=OQ时，t=8－3t，∴t=2．‎ 当OB2=PB·QO时，t(8－3t)=4，即3t2－8t+4=0．‎ 解得．‎ ‎②若P、Q在y轴的异侧．当PB=OQ时，3t－8=t，∴t=4．‎ 当OB2=PB·QO时，t(3t－8)=4，即3t2－8t－4=0．解得．‎ ‎∵t=<0．故舍去，∴t=．‎ ‎∴当t=2或t=或t=4或t=秒时，以P、B、O为顶点的三角形与以点Q、B、O为顶点的三角形相似．‎ ‎17．18．19．20．‎ ‎21．‎ ‎22． ‎ ‎23．24．25．26．27．28．29．30．‎