2019年甘肃省白银市中考数学试卷 23页

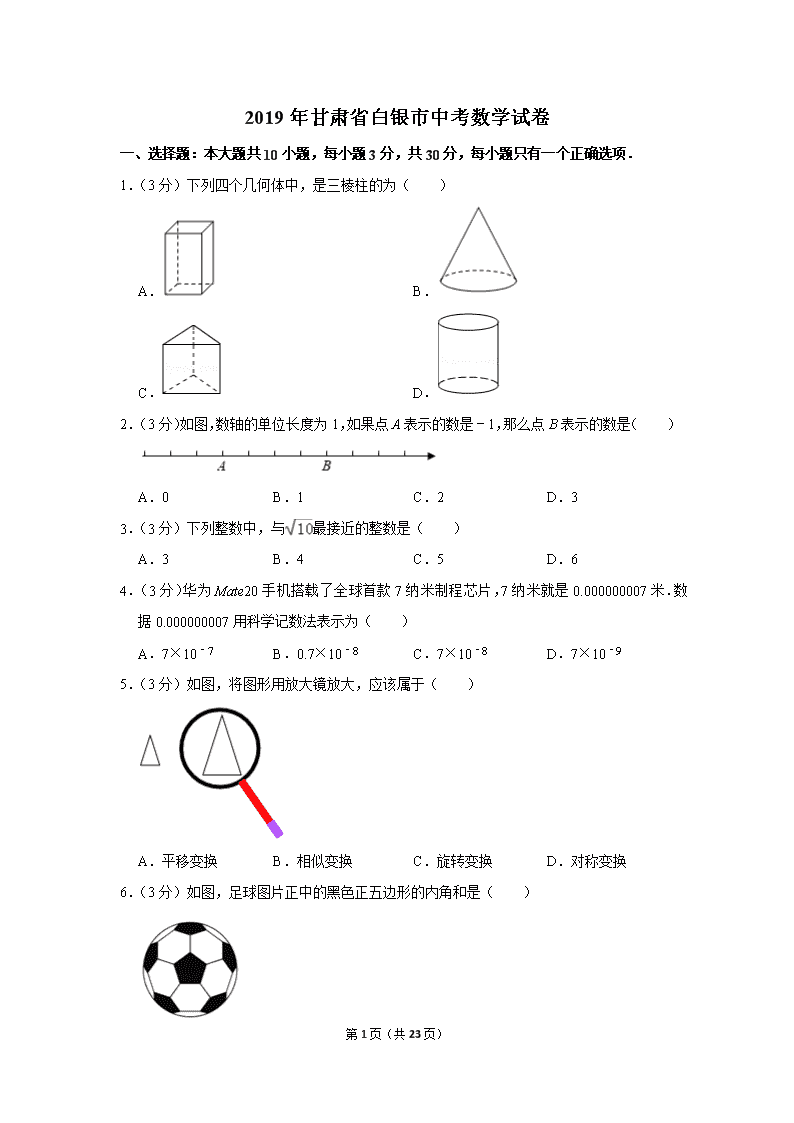
‎2019年甘肃省白银市中考数学试卷 一、选择题：本大题共10小题，每小题3分，共30分，每小题只有一个正确选项．‎ ‎1．（3分）下列四个几何体中，是三棱柱的为（　　）‎ A． B． ‎ C． D．‎ ‎2．（3分）如图，数轴的单位长度为1，如果点A表示的数是﹣1，那么点B表示的数是（　　）‎ A．0 B．1 C．2 D．3‎ ‎3．（3分）下列整数中，与最接近的整数是（　　）‎ A．3 B．4 C．5 D．6‎ ‎4．（3分）华为Mate20手机搭载了全球首款7纳米制程芯片，7纳米就是0.000000007米．数据0.000000007用科学记数法表示为（　　）‎ A．7×10﹣7 B．0.7×10﹣8 C．7×10﹣8 D．7×10﹣9‎ ‎5．（3分）如图，将图形用放大镜放大，应该属于（　　）‎ A．平移变换 B．相似变换 C．旋转变换 D．对称变换 ‎6．（3分）如图，足球图片正中的黑色正五边形的内角和是（　　）‎ 第23页（共23页）‎ 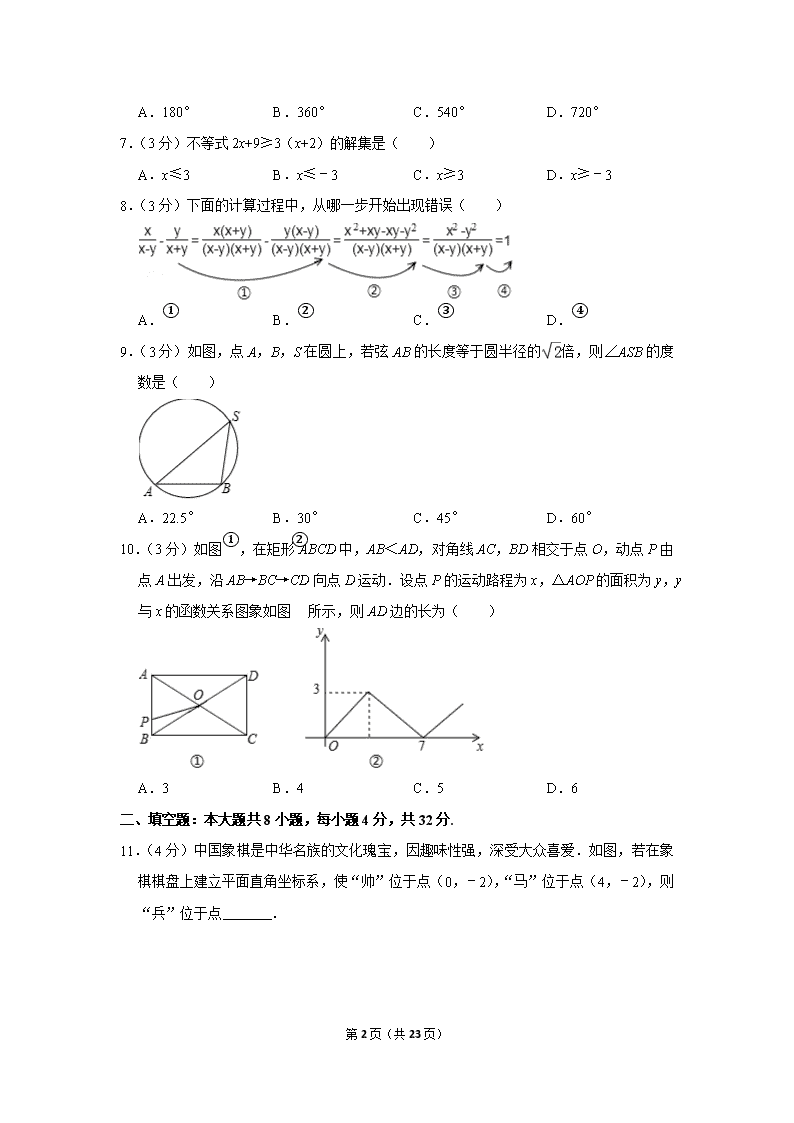A．180° B．360° C．540° D．720°‎ ‎7．（3分）不等式2x+9≥3（x+2）的解集是（　　）‎ A．x≤3 B．x≤﹣3 C．x≥3 D．x≥﹣3‎ ‎8．（3分）下面的计算过程中，从哪一步开始出现错误（　　）‎ A．① B．② C．③ D．④‎ ‎9．（3分）如图，点A，B，S在圆上，若弦AB的长度等于圆半径的倍，则∠ASB的度数是（　　）‎ A．22.5° B．30° C．45° D．60°‎ ‎10．（3分）如图①，在矩形ABCD中，AB＜AD，对角线AC，BD相交于点O，动点P由点A出发，沿AB→BC→CD向点D运动．设点P的运动路程为x，△AOP的面积为y，y与x的函数关系图象如图②所示，则AD边的长为（　　）‎ A．3 B．4 C．5 D．6‎ 二、填空题：本大题共8小题，每小题4分，共32分.‎ ‎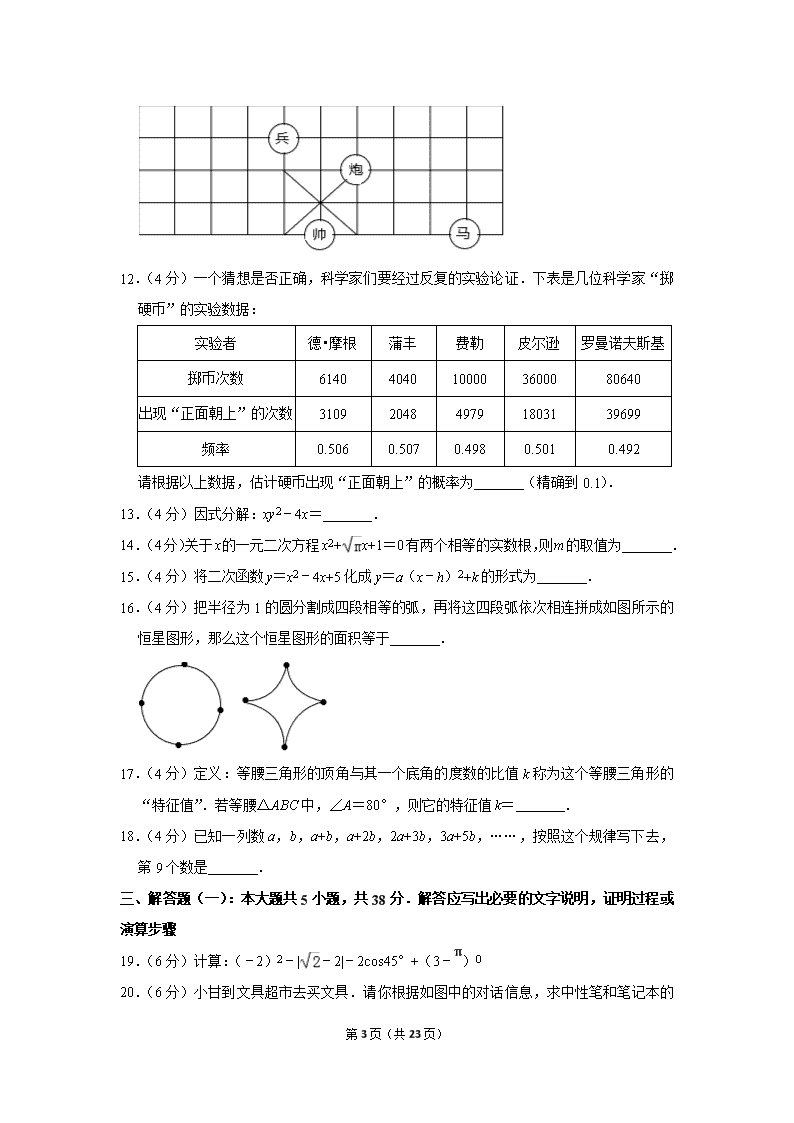11．（4分）中国象棋是中华名族的文化瑰宝，因趣味性强，深受大众喜爱．如图，若在象棋棋盘上建立平面直角坐标系，使“帅”位于点（0，﹣2），“马”位于点（4，﹣2），则“兵”位于点　 　．‎ 第23页（共23页）‎ ‎12．（4分）一个猜想是否正确，科学家们要经过反复的实验论证．下表是几位科学家“掷硬币”的实验数据：‎ 实验者 德•摩根 蒲丰 费勒 皮尔逊 罗曼诺夫斯基 掷币次数 ‎6140‎ ‎4040‎ ‎10000‎ ‎36000‎ ‎80640‎ 出现“正面朝上”的次数 ‎3109‎ ‎2048‎ ‎4979‎ ‎18031‎ ‎39699‎ 频率 ‎0.506‎ ‎0.507‎ ‎0.498‎ ‎0.501‎ ‎0.492‎ 请根据以上数据，估计硬币出现“正面朝上”的概率为　 　（精确到0.1）．‎ ‎13．（4分）因式分解：xy2﹣4x＝　 　．‎ ‎14．（4分）关于x的一元二次方程x2+x+1＝0有两个相等的实数根，则m的取值为　 　．‎ ‎15．（4分）将二次函数y＝x2﹣4x+5化成y＝a（x﹣h）2+k的形式为　 　．‎ ‎16．（4分）把半径为1的圆分割成四段相等的弧，再将这四段弧依次相连拼成如图所示的恒星图形，那么这个恒星图形的面积等于　 　．‎ ‎17．（4分）定义：等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”．若等腰△ABC中，∠A＝80°，则它的特征值k＝　 　．‎ ‎18．（4分）已知一列数a，b，a+b，a+2b，2a+3b，3a+5b，……，按照这个规律写下去，第9个数是　 　．‎ 三、解答题（一）：本大题共5小题，共38分．解答应写出必要的文字说明，证明过程或演算步骤 ‎19．（6分）计算：（﹣2）2﹣|﹣2|﹣2cos45°+（3﹣π）0‎ 第23页（共23页）‎ ‎20．（6分）小甘到文具超市去买文具．请你根据如图中的对话信息，求中性笔和笔记本的单价分别是多少元？‎ ‎21．（8分）已知：在△ABC中，AB＝AC．‎ ‎（1）求作：△ABC的外接圆．（要求：尺规作图，保留作图痕迹，不写作法）‎ ‎（2）若△ABC的外接圆的圆心O到BC边的距离为4，BC＝6，则S⊙O＝　 　．‎ ‎22．（8分）图①是放置在水平面上的台灯，图②是其侧面示意图（台灯底座高度忽略不计），其中灯臂AC＝40cm，灯罩CD＝30cm，灯臂与底座构成的∠CAB＝60°．CD可以绕点C上下调节一定的角度．使用发现：当CD与水平线所成的角为30°时，台灯光线最佳．现测得点D到桌面的距离为49.6cm．请通过计算说明此时台灯光线是否为最佳？（参考数据：取1.73）．‎ ‎23．（10分）2019年中国北京世界园艺博览会（以下简称“世园会”）于4月29日至10月7日在北京延庆区举行．世园会为满足大家的游览需求，倾情打造了4条各具特色的趣玩路线，分别是：A．“解密世园会”、B．“爱我家，爱园艺”、C．“园艺小清新之旅”和 第23页（共23页）‎ D．“快速车览之旅”．李欣和张帆都计划暑假去世园会，他们各自在这4条线路中任意选择一条线路游览，每条线路被选择的可能性相同．‎ ‎（1）李欣选择线路C．“园艺小清新之旅”的概率是多少？‎ ‎（2）用画树状图或列表的方法，求李欣和张帆恰好选择同一线路游览的概率．‎ 四、解答题（二）：本大题共5小题，共50分．解答应写出必要的文字说明，证明过程或演算步骤．‎ ‎24．（8分）为弘扬传统文化，某校开展了“传承经典文化，阅读经典名著”活动．为了解七、八年级学生（七、八年级各有600名学生）的阅读效果，该校举行了经典文化知识竞赛．现从两个年级各随机抽取20名学生的竞赛成绩（百分制）进行分析，过程如下：‎ 收集数据：‎ 七年级：79，85，73，80，75，76，87，70，75，94，75，79，81，71，75，80，86，59，83，77．‎ 八年级：92，74，87，82，72，81，94，83，77，83，80，81，71，81，72，77，82，80，70，41．‎ 整理数据：‎ ‎40≤x≤49‎ ‎50≤x≤59‎ ‎60≤x≤69‎ ‎70≤x≤79‎ ‎80≤x≤89‎ ‎90≤x≤100‎ 七年级 ‎0‎ ‎1‎ ‎0‎ a ‎7‎ ‎1‎ 八年级 ‎1‎ ‎0‎ ‎0‎ ‎7‎ b ‎2‎ 分析数据：‎ 平均数 众数 中位数 七年级 ‎78‎ ‎75‎ c 八年级 ‎78‎ d ‎80.5‎ 应用数据：‎ ‎（1）由上表填空：a＝　 　，b＝　 　，c＝　 　，d＝　 　．‎ ‎（2）估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人？‎ ‎（3）你认为哪个年级的学生对经典文化知识掌握的总体水平较好，请说明理由．‎ ‎25．（10分）如图，已知反比例函数y＝（k≠0）的图象与一次函数y＝﹣x+b的图象在第一象限交于A（1，3），B（3，1）两点 第23页（共23页）‎ ‎（1）求反比例函数和一次函数的表达式；‎ ‎（2）已知点P（a，0）（a＞0），过点P作平行于y轴的直线，在第一象限内交一次函数y＝﹣x+b的图象于点M，交反比例函数y＝上的图象于点N．若PM＞PN，结合函数图象直接写出a的取值范围．‎ ‎26．（10分）如图，在△ABC中，AB＝AC，∠BAC＝120°，点D在BC边上，⊙D经过点A和点B且与BC边相交于点E．‎ ‎（1）求证：AC是⊙D的切线；‎ ‎（2）若CE＝2，求⊙D的半径．‎ ‎27．（10分）阅读下面的例题及点拨，并解决问题：‎ 例题：如图①，在等边△ABC中，M是BC边上一点（不含端点B，C），N是△ABC的外角∠ACH的平分线上一点，且AM＝MN．求证：∠AMN＝60°．‎ 点拨：如图②，作∠CBE＝60°，BE与NC的延长线相交于点E，得等边△BEC，连接EM．易证：△ABM≌△EBM（SAS），可得AM＝EM，∠1＝∠2；又AM＝MN，则EM＝MN，可得∠3＝∠4；由∠3+∠1＝∠4+∠5＝60°，进一步可得∠1＝∠2＝∠5，又因为∠2+∠6＝120°，所以∠5+∠6＝120°，即：∠AMN＝60°．‎ 问题：如图③，在正方形A1B1C1D1中，M1是B1C1边上一点（不含端点B1，C1），N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点，且A1M1＝M1N1．求证：∠A1M1N1＝90°．‎ 第23页（共23页）‎ ‎28．（12分）如图，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，连接AC，BC．点P是第一象限内抛物线上的一个动点，点P的横坐标为m．‎ ‎（1）求此抛物线的表达式；‎ ‎（2）过点P作PM⊥x轴，垂足为点M，PM交BC于点Q．试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标，若不存在，请说明理由；‎ ‎（3）过点P作PN⊥BC，垂足为点N．请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？‎ 第23页（共23页）‎ ‎2019年甘肃省白银市中考数学试卷 参考答案与试题解析 一、选择题：本大题共10小题，每小题3分，共30分，每小题只有一个正确选项．‎ ‎1．（3分）下列四个几何体中，是三棱柱的为（　　）‎ A． B． ‎ C． D．‎ ‎【解答】解：A、该几何体为四棱柱，不符合题意；‎ B、该几何体为圆锥，不符合题意；‎ C、该几何体为三棱柱，符合题意；‎ D、该几何体为圆柱，不符合题意．‎ 故选：C．‎ ‎2．（3分）如图，数轴的单位长度为1，如果点A表示的数是﹣1，那么点B表示的数是（　　）‎ A．0 B．1 C．2 D．3‎ ‎【解答】解：∵数轴的单位长度为1，如果点A表示的数是﹣1，‎ ‎∴点B表示的数是：3．‎ 故选：D．‎ ‎3．（3分）下列整数中，与最接近的整数是（　　）‎ A．3 B．4 C．5 D．6‎ ‎【解答】解：∵32＝9，42＝16，‎ ‎∴3＜＜4，‎ ‎10与9的距离小于16与10的距离，‎ ‎∴与最接近的是3．‎ 故选：A．‎ 第23页（共23页）‎ ‎4．（3分）华为Mate20手机搭载了全球首款7纳米制程芯片，7纳米就是0.000000007米．数据0.000000007用科学记数法表示为（　　）‎ A．7×10﹣7 B．0.7×10﹣8 C．7×10﹣8 D．7×10﹣9‎ ‎【解答】解：0.000000007＝7×10﹣9；‎ 故选：D．‎ ‎5．（3分）如图，将图形用放大镜放大，应该属于（　　）‎ A．平移变换 B．相似变换 C．旋转变换 D．对称变换 ‎【解答】解：根据相似图形的定义知，用放大镜将图形放大，属于图形的形状相同，大小不相同，所以属于相似变换．‎ 故选：B．‎ ‎6．（3分）如图，足球图片正中的黑色正五边形的内角和是（　　）‎ A．180° B．360° C．540° D．720°‎ ‎【解答】解：黑色正五边形的内角和为：（5﹣2）×180°＝540°，‎ 故选：C．‎ ‎7．（3分）不等式2x+9≥3（x+2）的解集是（　　）‎ A．x≤3 B．x≤﹣3 C．x≥3 D．x≥﹣3‎ ‎【解答】解：去括号，得2x+9≥3x+6，‎ 移项，合并得﹣x≥﹣3‎ 系数化为1，得x≤3；‎ 故选：A．‎ ‎8．（3分）下面的计算过程中，从哪一步开始出现错误（　　）‎ 第23页（共23页）‎ A．① B．② C．③ D．④‎ ‎【解答】解：﹣‎ ‎＝﹣‎ ‎＝‎ ‎＝．‎ 故从第②步开始出现错误．‎ 故选：B．‎ ‎9．（3分）如图，点A，B，S在圆上，若弦AB的长度等于圆半径的倍，则∠ASB的度数是（　　）‎ A．22.5° B．30° C．45° D．60°‎ ‎【解答】解：设圆心为O，连接OA、OB，如图，‎ ‎∵弦AB的长度等于圆半径的倍，‎ 即AB＝OA，‎ ‎∴OA2+OB2＝AB2，‎ ‎∴△OAB为等腰直角三角形，∠AOB＝90°，‎ ‎∴∠ASB＝∠AOB＝45°．‎ 故选：C．‎ 第23页（共23页）‎ ‎10．（3分）如图①，在矩形ABCD中，AB＜AD，对角线AC，BD相交于点O，动点P由点A出发，沿AB→BC→CD向点D运动．设点P的运动路程为x，△AOP的面积为y，y与x的函数关系图象如图②所示，则AD边的长为（　　）‎ A．3 B．4 C．5 D．6‎ ‎【解答】解：当P点在AB上运动时，△AOP面积逐渐增大，当P点到达B点时，△AOP面积最大为3．‎ ‎∴AB•BC＝3，即AB•BC＝12．‎ 当P点在BC上运动时，△AOP面积逐渐减小，当P点到达C点时，△AOP面积为0，此时结合图象可知P点运动路径长为7，‎ ‎∴AB+BC＝7．‎ 则BC＝7﹣AB，代入AB•BC＝12，得AB2﹣7AB+12＝0，解得AB＝4或3，‎ 因为AB＜AD，即AB＜BC，‎ 所以AB＝3，BC＝4．‎ 故选：B．‎ 二、填空题：本大题共8小题，每小题4分，共32分.‎ ‎11．（4分）中国象棋是中华名族的文化瑰宝，因趣味性强，深受大众喜爱．如图，若在象棋棋盘上建立平面直角坐标系，使“帅”位于点（0，﹣2），“马”位于点（4，﹣2），则“兵”位于点　（﹣1，1）　．‎ ‎【解答】解：如图所示：可得原点位置，则“兵”位于（﹣1，1）．‎ 第23页（共23页）‎ 故答案为：（﹣1，1）．‎ ‎12．（4分）一个猜想是否正确，科学家们要经过反复的实验论证．下表是几位科学家“掷硬币”的实验数据：‎ 实验者 德•摩根 蒲丰 费勒 皮尔逊 罗曼诺夫斯基 掷币次数 ‎6140‎ ‎4040‎ ‎10000‎ ‎36000‎ ‎80640‎ 出现“正面朝上”的次数 ‎3109‎ ‎2048‎ ‎4979‎ ‎18031‎ ‎39699‎ 频率 ‎0.506‎ ‎0.507‎ ‎0.498‎ ‎0.501‎ ‎0.492‎ 请根据以上数据，估计硬币出现“正面朝上”的概率为　0.5　（精确到0.1）．‎ ‎【解答】解：因为表中硬币出现“正面朝上”的频率在0.5左右波动，‎ 所以估计硬币出现“正面朝上”的概率为0.5．‎ 故答案为0.5．‎ ‎13．（4分）因式分解：xy2﹣4x＝　x（y+2）（y﹣2）　．‎ ‎【解答】解：xy2﹣4x，‎ ‎＝x（y2﹣4），‎ ‎＝x（y+2）（y﹣2）．‎ ‎14．（4分）关于x的一元二次方程x2+x+1＝0有两个相等的实数根，则m的取值为　4　．‎ ‎【解答】解：‎ 由题意，△＝b2﹣4ac＝（）2﹣4＝0‎ 得m＝4‎ 故答案为4‎ ‎15．（4分）将二次函数y＝x2﹣4x+5化成y＝a（x﹣h）2+k的形式为　y＝（x﹣2）2+1　．‎ ‎【解答】解：y＝x2﹣4x+5＝x2﹣4x+4+1＝（x﹣2）2+1，‎ 第23页（共23页）‎ 所以，y＝（x﹣2）2+1．‎ 故答案为：y＝（x﹣2）2+1．‎ ‎16．（4分）把半径为1的圆分割成四段相等的弧，再将这四段弧依次相连拼成如图所示的恒星图形，那么这个恒星图形的面积等于　4﹣π　．‎ ‎【解答】解：如图：‎ 新的正方形的边长为1+1＝2，‎ ‎∴恒星的面积＝2×2﹣π＝4﹣π．‎ 故答案为4﹣π．‎ ‎17．（4分）定义：等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”．若等腰△ABC中，∠A＝80°，则它的特征值k＝　或　．‎ ‎【解答】解：‎ ‎①当∠A为顶角时，等腰三角形两底角的度数为：＝50°‎ ‎∴特征值k＝＝‎ ‎②当∠A为底角时，顶角的度数为：180°﹣80°﹣80°＝20°‎ ‎∴特征值k＝＝‎ 综上所述，特征值k为或 故答案为或 ‎18．（4分）已知一列数a，b，a+b，a+2b，2a+3b，3a+5b，……，按照这个规律写下去，第9个数是　13a+21b　．‎ ‎【解答】解：由题意知第7个数是5a+8b，第8个数是8a+13b，第9个数是13a+21b，‎ 故答案为：13a+21b．‎ 第23页（共23页）‎ 三、解答题（一）：本大题共5小题，共38分．解答应写出必要的文字说明，证明过程或演算步骤 ‎19．（6分）计算：（﹣2）2﹣|﹣2|﹣2cos45°+（3﹣π）0‎ ‎【解答】解：（﹣2）2﹣|﹣2|﹣2cos45°+（3﹣π）0，‎ ‎＝4﹣（2﹣）﹣2×+1，‎ ‎＝4﹣2+﹣+1，‎ ‎＝3．‎ ‎20．（6分）小甘到文具超市去买文具．请你根据如图中的对话信息，求中性笔和笔记本的单价分别是多少元？‎ ‎【解答】解：设中性笔和笔记本的单价分别是x元、y元，根据题意可得：‎ ‎，‎ 解得：，‎ 答：中性笔和笔记本的单价分别是2元、6元．‎ ‎21．（8分）已知：在△ABC中，AB＝AC．‎ ‎（1）求作：△ABC的外接圆．（要求：尺规作图，保留作图痕迹，不写作法）‎ ‎（2）若△ABC的外接圆的圆心O到BC边的距离为4，BC＝6，则S⊙O＝　25π　．‎ ‎【解答】解：（1）如图⊙O即为所求．‎ 第23页（共23页）‎ ‎（2）设线段BC的垂直平分线交BC于点E．‎ 由题意OE＝4，BE＝EC＝3，‎ 在Rt△OBE中，OB＝＝5，‎ ‎∴S圆O＝π•52＝25π．‎ 故答案为25π．‎ ‎22．（8分）图①是放置在水平面上的台灯，图②是其侧面示意图（台灯底座高度忽略不计），其中灯臂AC＝40cm，灯罩CD＝30cm，灯臂与底座构成的∠CAB＝60°．CD可以绕点C上下调节一定的角度．使用发现：当CD与水平线所成的角为30°时，台灯光线最佳．现测得点D到桌面的距离为49.6cm．请通过计算说明此时台灯光线是否为最佳？（参考数据：取1.73）．‎ ‎【解答】解：如图，作CE⊥AB于E，DH⊥AB于H，CF⊥DH于F．‎ 第23页（共23页）‎ ‎∵∠CEH＝∠CFH＝∠FHE＝90°，‎ ‎∴四边形CEHF是矩形，‎ ‎∴CE＝FH，‎ 在Rt△ACE中，∵AC＝40cm，∠A＝60°，‎ ‎∴CE＝AC•sin60°＝34.6（cm），‎ ‎∴FH＝CE＝34.6（cm）‎ ‎∵DH＝49.6cm，‎ ‎∴DF＝DH﹣FH＝49.6﹣34.6＝15（cm），‎ 在Rt△CDF中，sin∠DCF＝＝＝，‎ ‎∴∠DCF＝30°，‎ ‎∴此时台灯光线为最佳．‎ ‎23．（10分）2019年中国北京世界园艺博览会（以下简称“世园会”）于4月29日至10月7日在北京延庆区举行．世园会为满足大家的游览需求，倾情打造了4条各具特色的趣玩路线，分别是：A．“解密世园会”、B．“爱我家，爱园艺”、C．“园艺小清新之旅”和D．“快速车览之旅”．李欣和张帆都计划暑假去世园会，他们各自在这4条线路中任意选择一条线路游览，每条线路被选择的可能性相同．‎ ‎（1）李欣选择线路C．“园艺小清新之旅”的概率是多少？‎ ‎（2）用画树状图或列表的方法，求李欣和张帆恰好选择同一线路游览的概率．‎ ‎【解答】解：（1）在这四条线路任选一条，每条被选中的可能性相同，‎ ‎∴在四条线路中，李欣选择线路C．“园艺小清新之旅”的概率是；‎ ‎（2）画树状图分析如下：‎ 共有16种等可能的结果，李欣和张帆恰好选择同一线路游览的结果有4种，‎ ‎∴李欣和张帆恰好选择同一线路游览的概率为＝．‎ 第23页（共23页）‎ 四、解答题（二）：本大题共5小题，共50分．解答应写出必要的文字说明，证明过程或演算步骤．‎ ‎24．（8分）为弘扬传统文化，某校开展了“传承经典文化，阅读经典名著”活动．为了解七、八年级学生（七、八年级各有600名学生）的阅读效果，该校举行了经典文化知识竞赛．现从两个年级各随机抽取20名学生的竞赛成绩（百分制）进行分析，过程如下：‎ 收集数据：‎ 七年级：79，85，73，80，75，76，87，70，75，94，75，79，81，71，75，80，86，59，83，77．‎ 八年级：92，74，87，82，72，81，94，83，77，83，80，81，71，81，72，77，82，80，70，41．‎ 整理数据：‎ ‎40≤x≤49‎ ‎50≤x≤59‎ ‎60≤x≤69‎ ‎70≤x≤79‎ ‎80≤x≤89‎ ‎90≤x≤100‎ 七年级 ‎0‎ ‎1‎ ‎0‎ a ‎7‎ ‎1‎ 八年级 ‎1‎ ‎0‎ ‎0‎ ‎7‎ b ‎2‎ 分析数据：‎ 平均数 众数 中位数 七年级 ‎78‎ ‎75‎ c 八年级 ‎78‎ d ‎80.5‎ 应用数据：‎ ‎（1）由上表填空：a＝　11　，b＝　10　，c＝　78　，d＝　81　．‎ ‎（2）估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人？‎ ‎（3）你认为哪个年级的学生对经典文化知识掌握的总体水平较好，请说明理由．‎ ‎【解答】解：（1）由题意知a＝11，b＝10，‎ 将七年级成绩重新排列为：59，70，71，73，75，75，75，75，76，77，79，79，80，80，81，83，85，86，87，94，‎ 第23页（共23页）‎ ‎∴其中位数c＝＝78，‎ 八年级成绩的众数d＝81，‎ 故答案为：11，10，78，81；‎ ‎（2）估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有1200×＝90（人）；‎ ‎（3）八年级的总体水平较好，‎ ‎∵七、八年级的平均成绩相等，而八年级的中位数大于七年级的中位数，‎ ‎∴八年级得分高的人数相对较多，‎ ‎∴八年级的学生对经典文化知识掌握的总体水平较好（答案不唯一，合理即可）．‎ ‎25．（10分）如图，已知反比例函数y＝（k≠0）的图象与一次函数y＝﹣x+b的图象在第一象限交于A（1，3），B（3，1）两点 ‎（1）求反比例函数和一次函数的表达式；‎ ‎（2）已知点P（a，0）（a＞0），过点P作平行于y轴的直线，在第一象限内交一次函数y＝﹣x+b的图象于点M，交反比例函数y＝上的图象于点N．若PM＞PN，结合函数图象直接写出a的取值范围．‎ ‎【解答】解：（1）∵反比例函数y＝（k≠0）的图象与一次函数y＝﹣x+b的图象在第一象限交于A（1，3），B（3，1）两点，‎ ‎∴3＝，3＝﹣1+b，‎ ‎∴k＝3，b＝4，‎ 第23页（共23页）‎ ‎∴反比例函数和一次函数的表达式分别为y＝，y＝﹣x+4；‎ ‎（2）由图象可得：当1＜a＜3时，PM＞PN．‎ ‎26．（10分）如图，在△ABC中，AB＝AC，∠BAC＝120°，点D在BC边上，⊙D经过点A和点B且与BC边相交于点E．‎ ‎（1）求证：AC是⊙D的切线；‎ ‎（2）若CE＝2，求⊙D的半径．‎ ‎【解答】（1）证明：连接AD，‎ ‎∵AB＝AC，∠BAC＝120°，‎ ‎∴∠B＝∠C＝30°，‎ ‎∵AD＝BD，‎ ‎∴∠BAD＝∠B＝30°，‎ ‎∴∠ADC＝60°，‎ ‎∴∠DAC＝180°﹣60°﹣30°＝90°，‎ ‎∴AC是⊙D的切线；‎ ‎（2）解：连接AE，‎ ‎∵AD＝DE，∠ADE＝60°，‎ ‎∴△ADE是等边三角形，‎ ‎∴AE＝DE，∠AED＝60°，‎ ‎∴∠EAC＝∠AED﹣∠C＝30°，‎ 第23页（共23页）‎ ‎∴∠EAC＝∠C，‎ ‎∴AE＝CE＝2，‎ ‎∴⊙D的半径AD＝2．‎ ‎27．（10分）阅读下面的例题及点拨，并解决问题：‎ 例题：如图①，在等边△ABC中，M是BC边上一点（不含端点B，C），N是△ABC的外角∠ACH的平分线上一点，且AM＝MN．求证：∠AMN＝60°．‎ 点拨：如图②，作∠CBE＝60°，BE与NC的延长线相交于点E，得等边△BEC，连接EM．易证：△ABM≌△EBM（SAS），可得AM＝EM，∠1＝∠2；又AM＝MN，则EM＝MN，可得∠3＝∠4；由∠3+∠1＝∠4+∠5＝60°，进一步可得∠1＝∠2＝∠5，又因为∠2+∠6＝120°，所以∠5+∠6＝120°，即：∠AMN＝60°．‎ 问题：如图③，在正方形A1B1C1D1中，M1是B1C1边上一点（不含端点B1，C1），N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点，且A1M1＝M1N1．求证：∠A1M1N1＝90°．‎ ‎【解答】解：延长A1B1至E，使EB1＝A1B1，连接EM1C、EC1，如图所示：‎ 则EB1＝B1C1，∠EB1M1中＝90°＝∠A1B1M1，‎ ‎∴△EB1C1是等腰直角三角形，‎ ‎∴∠B1EC1＝∠B1C1E＝45°，‎ ‎∵N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点，‎ 第23页（共23页）‎ ‎∴∠M1C1N1＝90°+45°＝135°，‎ ‎∴∠B1C1E+∠M1C1N1＝180°，‎ ‎∴E、C1、N1，三点共线，‎ 在△A1B1M1和△EB1M1中，，‎ ‎∴△A1B1M1≌△EB1M1（SAS），‎ ‎∴A1M1＝EM1，∠1＝∠2，‎ ‎∵A1M1＝M1N1，‎ ‎∴EM1＝M1N1，‎ ‎∴∠3＝∠4，‎ ‎∵∠2+∠3＝45°，∠4+∠5＝45°，‎ ‎∴∠1＝∠2＝∠5，‎ ‎∵∠1+∠6＝90°，‎ ‎∴∠5+∠6＝90°，‎ ‎∴∠A1M1N1＝180°﹣90°＝90°．‎ ‎28．（12分）如图，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，连接AC，BC．点P是第一象限内抛物线上的一个动点，点P的横坐标为m．‎ ‎（1）求此抛物线的表达式；‎ ‎（2）过点P作PM⊥x轴，垂足为点M，PM交BC于点Q．试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标，若不存在，请说明理由；‎ ‎（3）过点P作PN⊥BC，垂足为点N．请用含m的代数式表示线段PN的长，并求出当 第23页（共23页）‎ m为何值时PN有最大值，最大值是多少？‎ ‎【解答】解：（1）由二次函数交点式表达式得：y＝a（x+3）（x﹣4）＝a（x2﹣x﹣12）＝ax2﹣ax﹣12a，‎ 即：﹣12a＝4，解得：a＝﹣，‎ 则抛物线的表达式为y＝﹣x2+x+4；‎ ‎（2）存在，理由：‎ 点A、B、C的坐标分别为（﹣3，0）、（4，0）、（0，4），‎ 则AC＝5，AB＝7，BC＝4，∠OAB＝∠OBA＝45°，‎ 将点B、C的坐标代入一次函数表达式：y＝kx+b并解得：y＝﹣x+4…①，‎ 同理可得直线AC的表达式为：y＝x+4，‎ 设直线AC的中点为K（﹣，2），过点M与CA垂直直线的表达式中的k值为﹣，‎ 同理可得过点K与直线AC垂直直线的表达式为：y＝﹣x+…②，‎ ‎①当AC＝AQ时，如图1，‎ 第23页（共23页）‎ 则AC＝AQ＝5，‎ 设：QM＝MB＝n，则AM＝7﹣n，‎ 由勾股定理得：（7﹣n）2+n2＝25，解得：n＝3或4（舍去4），‎ 故点Q（1，3）；‎ ‎②当AC＝CQ时，如图1，‎ CQ＝5，则BQ＝BC﹣CQ＝4﹣5，‎ 则QM＝MB＝，‎ 故点Q（，）；‎ ‎③当CQ＝AQ时，‎ 联立①②并解得：x＝（舍去）；‎ 故点Q的坐标为：Q（1，3）或（，）；‎ ‎（3）设点P（m，﹣m2+m+4），则点Q（m，﹣m+4），‎ ‎∵OB＝OC，∴∠ABC＝∠OCB＝45°＝∠PQN，‎ PN＝PQsin∠PQN＝（﹣m2+m+4+m﹣4）＝﹣（m﹣2）2+，‎ ‎∵﹣＜0，∴PN有最大值，‎ 当m＝2时，PN的最大值为：．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/7/13 9:10:28；用户：柯瑞；邮箱：ainixiaoke00@163.com；学号：500557‎ 第23页（共23页）‎