中考数学压轴题练习20120318 10页

‎2011福州21‎ ‎（课余时间做）21、已知，矩形ABCD中，AB=‎4cm，BC=‎8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O． （1）如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长； （2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中， ①已知点P的速度为每秒‎5cm，点Q的速度为每秒‎4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值． ②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式． ‎ ‎2011福州22‎ ‎****22、已知，如图，二次函数y=ax2+2ax‎-3a（a≠0）图象的顶点为H，与x轴交于A、B两点（B在A点右侧），点H、B关于直线对称． （1）求A、B两点坐标，并证明点A在直线l上； （2）求二次函数解析式； （3）过点B作直线BK∥AH交直线l于K点，M、N分别为直线AH和直线l上的两个动点，连接HN、NM、MK，求HN+NM+MK和的最小值．‎ ‎****2011平谷模拟25‎ ‎****2011海淀模拟25‎ ‎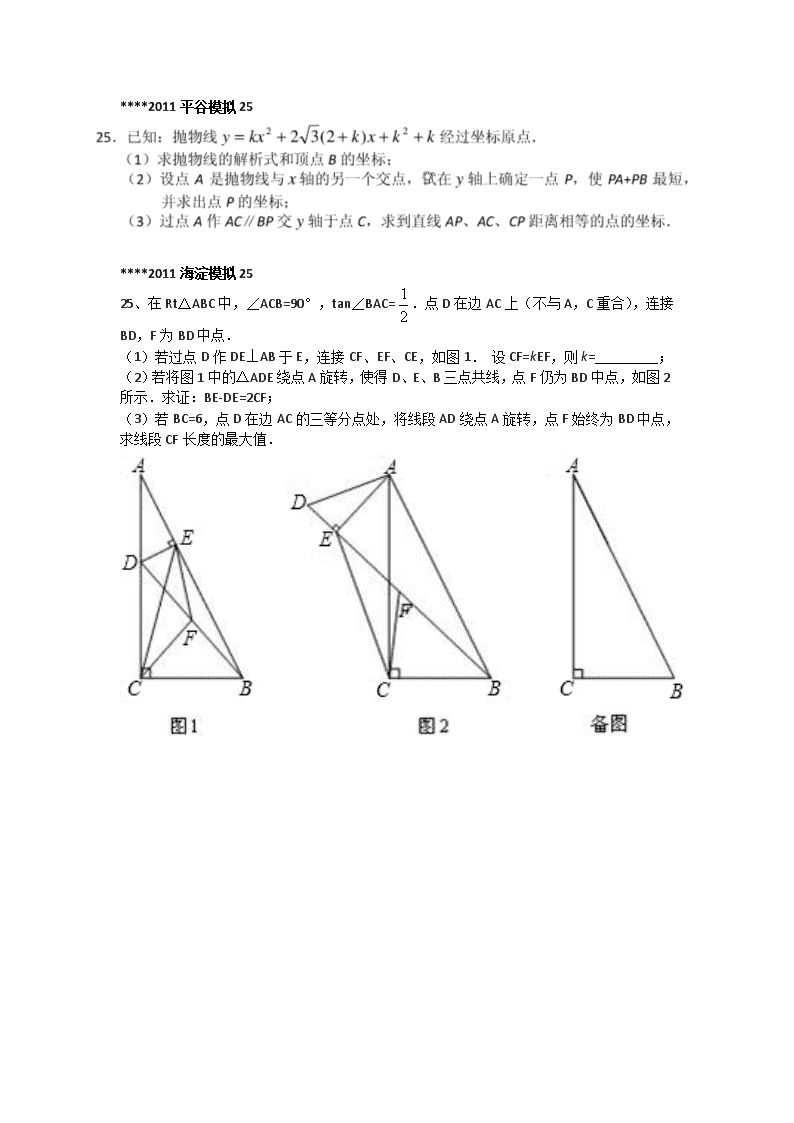25、在Rt△ABC中，∠ACB=90°，tan∠BAC=．点D在边AC上（不与A，C重合），连接BD，F为BD中点．‎ ‎（1）若过点D作DE⊥AB于E，连接CF、EF、CE，如图1． 设CF=kEF，则k= ；‎ ‎（2）若将图1中的△ADE绕点A旋转，使得D、E、B三点共线，点F仍为BD中点，如图2所示．求证：BE-DE=2CF；‎ ‎（3）若BC=6，点D在边AC的三等分点处，将线段AD绕点A旋转，点F始终为BD中点，求线段CF长度的最大值．‎ ‎****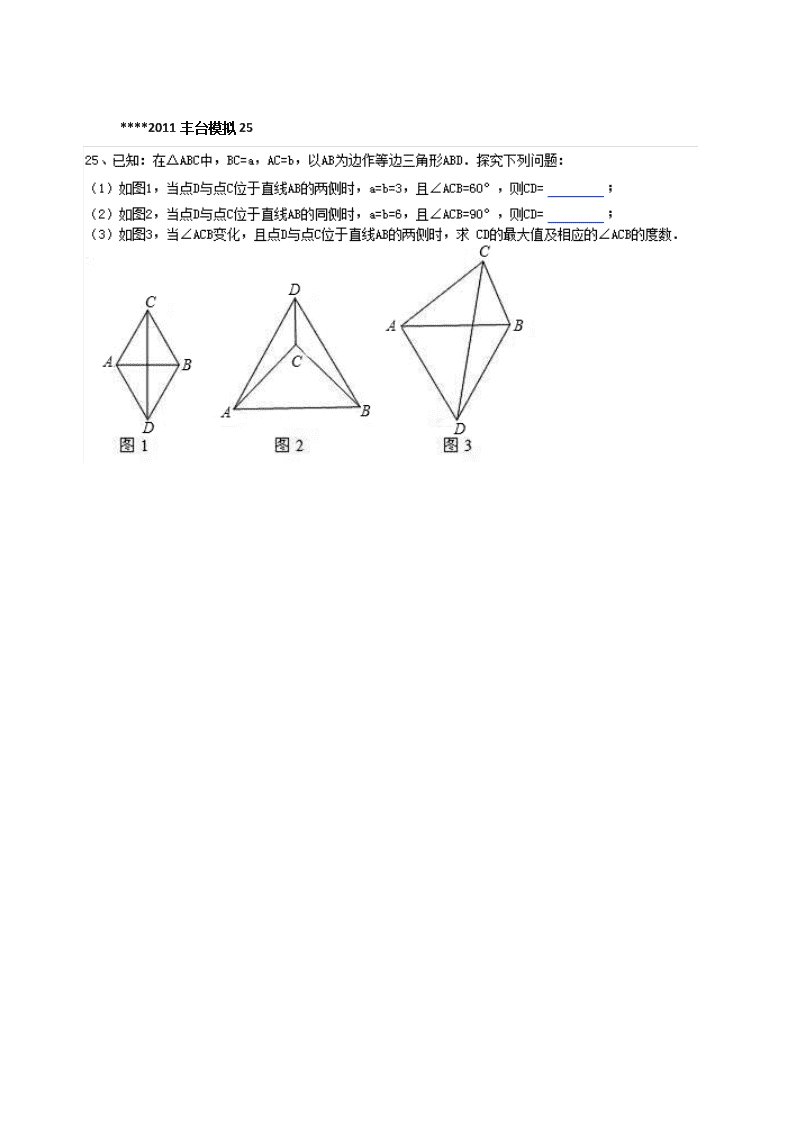2011丰台模拟25‎ ‎****2011房山模拟25‎ ‎****2010南通28‎ ‎28．（本小题满分14分）‎ 已知抛物线y＝ax 2＋bx＋c经过A（－4，3）、B（2，0）两点，当x＝3和x＝－3时，这条抛物线上对应点的纵坐标相等．经过点C（0，－2）的直线l与x轴平行，O为坐标原点．‎ ‎（1）求直线AB和这条抛物线的解析式；‎ ‎（2）以A为圆心，AO为半径的圆记为⊙A，判断直线l与⊙A的位置关系，并说明理由；‎ ‎（3）设直线AB上的点D的横坐标为－1，P（m，n）是抛物线y＝ax 2＋bx＋c上的动点，当△PDO的周长最小时，求四边形CODP的面积．‎ O x y O x y ‎2010中山22‎ ‎2010聊城25‎ ‎25、如图，已知抛物线（a≠0）的对称轴为x=1，且抛物线经过A（-1，0）、C（0，-3）两点，与x轴交于另一点B．‎ ‎（1）求这条抛物线所对应的函数关系式；‎ ‎（2）在抛物线的对称轴x=1上求一点M，使点M到点A的距离与到点C的距离之和最小，并求出此时点M的坐标；‎ ‎（3）设点P为抛物线的对称轴x=1上的一动点，求使∠PCB=90°的点P的坐标．‎ ‎2011上海徐汇模拟25‎ ‎25.在梯形ABCD中，AD//BC，AB⊥AD，AB=4，AD=5，CD=5．E为底边BC上一点，以点E为圆心，BE为半径画⊙E交直线DE于点F． ‎ (1) 如图，当点F在线段DE上时，设BE，DF，试建立关于的函数关系式，‎ 并写出自变量的取值范围； ‎ (2) 当以CD直径的⊙O与⊙E与相切时，求的值；‎ (3) 联接AF、BF，当△ABF是以AF为腰的等腰三角形时，求的值。‎ ‎2011上海卢湾模拟25‎ ‎25、已知：如图，在直角梯形ABCD中，BC∥AD （AD＞BC），BC⊥AB，AB=8，BC=6．动点E、F分别在边BC和AD上，且AF=2EC．线段EF与AC相交于点G，过点G作GH∥AD，交CD于点H，射线EH交AD的延长线于点M，交AC于点O，设EC=x．‎ ‎（1）求证：AF=DM；‎ ‎（2）当EM⊥AC时，用含x的代数式表达AD的长；‎ ‎（3）在（2）题条件下，若以MO为半径的⊙M与以FD为半径的⊙F相切，求x的值．‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎-1‎ O 第24题图 ‎-1‎ ‎5‎ ‎2011上海虹口模拟24‎ ‎24．（本题满分12分，第（1）小题6分，第（2）小题6分）‎ 在平面直角坐标系中，抛物线经过点（0，2）和点（3，5）．‎ ‎（1）求该抛物线的表达式并写出顶点坐标；‎ ‎（2）点P为抛物线上一动点，如果直径为4的 ‎⊙P与轴相切，求点P的坐标.‎ ‎2011上海奉贤模拟25‎ ‎25．（本题满分14分，第（1）、（2）小题每小题满分5分，第（3）小题满分4分）‎ 已知，在边长为6的正方形ABCD的两侧如图作正方形BEFG、正方形DMNK，恰好使得N、A、F三点在一直线上，联结MF交线段AD于点P，联结NP，设正方形BEFG的边长为x，正方形DMNK的边长为y，‎ ‎（1）求y关于x的函数关系式及自变量x的取值范围；‎ ‎（2）当△NPF的面积为32时，求x的值；‎ ‎（3）以P为圆心，AP为半径的圆能否与以G为圆心，GF为半径的圆相切，若能请求x的值，若不能，请说明理由。‎ A B C D E F G M N K P 第25题图 ‎ ‎ ‎2010盐城27‎ ‎27、如图1所示，在直角梯形ABCD中，AD∥BC，AB⊥BC，∠DCB=75°，以CD为一边的等边△DCE的另一顶点E在腰AB上．‎ ‎（1）求∠AED的度数；‎ ‎（2）求证：AB=BC；‎ ‎（3）如图2所示，若F为线段CD上一点，∠FBC=30°，求的值．‎ ‎2010盐城28‎ ‎28、已知：函数y=ax2+x+1的图象与x轴只有一个公共点．‎ ‎（1）求这个函数关系式；‎ ‎（2）如图所示，设二次函数y=ax2+x+1图象的顶点为B，与y轴的交点为A，P为图象上的一点，若以线段PB为直径的圆与直线AB相切于点B，求P点的坐标；‎ ‎（3）在（2）中，若圆与x轴另一交点关于直线PB的对称点为M，试探索点M是否在抛物线y=ax2+x+1上？若在抛物线上，求出M点的坐标；若不在，请说明理由．‎ ‎2010泰州27‎ ‎27.（12分）‎ ‎2010泰州28‎ ‎28.（14分）如图，⊙O是O为圆心，半径为的圆，直线交坐标轴于A、B两点。‎ ‎(1)若OA=OB ‎①求k ‎②若b=4，点P为直线AB上一点，过P点作⊙O的两条切线，切点分别这C、D，若∠CPD=90°，求点P的坐标；‎ ‎(2)若，且直线分⊙O的圆周为1：2两部分，求b.‎ ‎****2010福州22‎ ‎22、如图1，在平面直角坐标系中，点B在直线y=2x上，过点B作x轴的垂线，垂足为A，OA=5．若抛物线过点O、A两点．‎ ‎（1）求该抛物线的解析式；‎ ‎（2）若A点关于直线y=2x的对称点为C，判断点C是否在该抛物线上，并说明理由；‎ ‎（3）如图2，在（2）的条件下，⊙O1是以BC为直径的圆．过原点O作O1的切线OP，P为切点（P与点C不重合），抛物线上是否存在点Q，使得以PQ为直径的圆与O1相切？若存在，求出点Q的横坐标；若不存在，请说明理由．‎ ‎2011南通28‎ ‎28、如图，已知直线l经过点A（1，0），与双曲线y=（x＞0）交于点B（2，1）．过点P（p，p-1）（p＞1）作x轴的平行线分别交双曲线y=（x＞0）和y=（x＜0）于点M、N． （1）求m的值和直线l的解析式； （2）若点P在直线y=2上，求证：△PMB∽△PNA； （3）是否存在实数p，使得S△AMN=4S△AMP？若存在，请求出所有满足条件的p的值；若不存在，请说明理由．‎ ‎2011上海松江模拟24‎ ‎24．（本题满分12分，第（1）小题3分，第（2）①小题4分，第（2）②小题5分）‎ 如图，在平面直角坐标系xoy中，直角梯形OABC的顶点O为坐标原点，顶点A、C分别在x轴、y轴的正半轴上，CB∥OA， OC=4， BC=3，OA=5，点D在边OC上，CD=3，过点D作DB的垂线DE，交x轴于点E． ‎ ‎（1）求点E的坐标；‎ ‎（2）二次函数的图象经过点B和点E．‎ ‎①求二次函数的解析式和它的对称轴；‎ ‎②如果点M在它的对称轴上且位于x轴上方，满足，求点M的坐标．‎ A y C B D O x E ‎（第24题图）‎