中考数学压轴题精选四及答案 19页

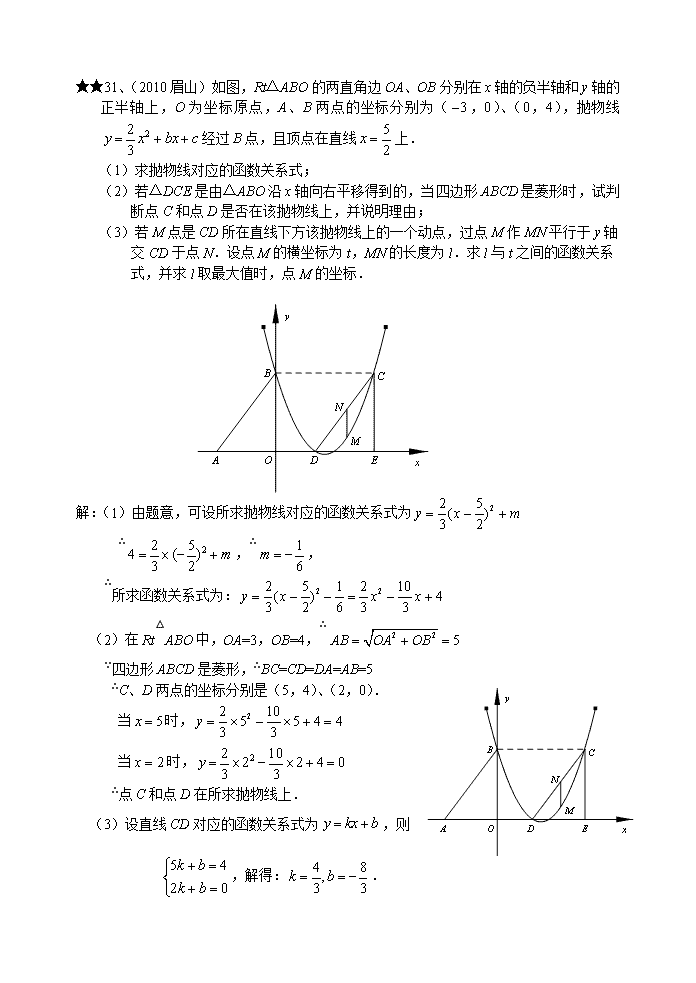
‎★★31、（2010眉山）如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为（，0）、（0，4），抛物线经过B点，且顶点在直线上．‎ ‎（1）求抛物线对应的函数关系式；‎ ‎（2）若△DCE是由△ABO沿x轴向右平移得到的，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由；‎ ‎（3）若M点是CD所在直线下方该抛物线上的一个动点，过点M作MN平行于y轴交CD于点N．设点M的横坐标为t，MN的长度为l．求l与t之间的函数关系式，并求l取最大值时，点M的坐标．‎ 解：（1）由题意，可设所求抛物线对应的函数关系式为 ‎ ‎ ∴，∴，‎ ‎∴所求函数关系式为： ‎ ‎（2）在Rt△ABO中，OA=3，OB=4，∴‎ ‎∵四边形ABCD是菱形，∴BC=CD=DA=AB=5 ‎ ‎∴C、D两点的坐标分别是（5，4）、（2，0）． ‎ 当时，‎ 当时，‎ ‎∴点C和点D在所求抛物线上． ‎ ‎（3）设直线CD对应的函数关系式为，则 ‎，解得：．‎ ‎∴，∵MN∥y轴，M点的横坐标为t，∴N点的横坐标也为t．‎ 则， ， ‎ ‎∴‎ ‎∵， ∴当时，，此时点M的坐标为（，）． ‎ ‎★★32、（2010绵阳）如图，抛物线y = ax2 + bx + 4与x轴的两个交点分别为A（－4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．‎ ‎（1）求抛物线的函数解析式，并写出顶点D的坐标；‎ ‎（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；‎ ‎（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．‎ C E D G A x y O B F 解：（1）由题意，得 解得，b =－1．‎ 所以抛物线的解析式为，顶点D的坐标为（－1，）．‎ ‎（2）设抛物线的对称轴与x轴交于点M．因为EF垂直平分BC，即C关于直线EG的对称点为B，连结BD交于EF于一点，则这一点为所求点H，使DH + CH最小，即最小为 DH + CH = DH + HB = BD =． 而 ．‎ ‎∴ △CDH的周长最小值为CD + DR + CH =．‎ 设直线BD的解析式为y = k1x + b，则 解得 ，b1 = 3．‎ 所以直线BD的解析式为y =x + 3．‎ 由于BC = 2，CE = BC∕2 =，Rt△CEG∽△COB，‎ 得 CE : CO = CG : CB，所以 CG = 2.5，GO = 1.5．G（0，1.5）．‎ 同理可求得直线EF的解析式为y =x +．‎ 联立直线BD与EF的方程，解得使△CDH的周长最小的点H（，）．‎ ‎（3）设K（t，），xF＜t＜xE．过K作x轴的垂线交EF于N．‎ 则 KN = yK－yN =－（t +）=．‎ 所以 S△EFK = S△KFN + S△KNE =KN（t + 3）+KN（1－t）= 2KN = －t2－3t + 5 =－（t +）2 +．即当t =－时，△EFK的面积最大，最大面积为，此时K（－，）．‎ ‎★★33、（2010南充）已知抛物线上有不同的两点E和F．‎ ‎（1）求抛物线的解析式．‎ ‎（2）如图，抛物线与x轴和y轴的正半轴分别交于点A和B，M为AB的中点，∠PMQ在AB的同侧以M为中心旋转，且∠PMQ＝45°，MP交y轴于点C，MQ交x轴于点D．设AD的长为m（m＞0），BC的长为n，求n和m之间的函数关系式．‎ ‎（3）当m，n为何值时，∠PMQ的边过点F．‎ ‎　　‎B A M C D O P Q x y 解：（1）抛物线的对称轴为．　 ∵　抛物线上不同两个点E和F的纵坐标相同， ∴　点E和点F关于抛物线对称轴对称，则　，且k≠－2． ∴　抛物线的解析式为．　　　　　　　　　　　　 （2）抛物线与x轴的交点为A（4，0），与y轴的交点为B（0，4）， ∴　AB＝，AM＝BM＝．　　　　　　　　　　　　　　　　‎ 在∠PMQ绕点M在AB同侧旋转过程中，∠MBC＝∠DAM＝∠PMQ＝45°， 在△BCM中，∠BMC＋∠BCM＋∠MBC＝180°，即∠BMC＋∠BCM＝135°， 在直线AB上，∠BMC＋∠PMQ＋∠AMD＝180°，即∠BMC＋∠AMD＝135°． ∴　∠BCM＝∠AMD． 故　△BCM∽△AMD．　　　　　　　　　　　　　　　　　　　　　 ∴　，即　，． 故n和m之间的函数关系式为（m＞0）．　　　　　　　　　　 （3）∵　F在上， 　　 ∴　， 　　化简得，，∴　k1＝1，k2＝3．　　　　 ‎ ‎　　即F1（－2，0）或F2（－4，－8）．　　　　　　　　　　　　　 　　①MF过M（2，2）和F1（－2，0），设MF为， 　　则　　　解得，　∴　直线MF的解析式为． 　　直线MF与x轴交点为（－2，0），与y轴交点为（0，1）． 　　若MP过点F（－2，0），则n＝4－1＝3，m＝； 　　若MQ过点F（－2，0），则m＝4－（－2）＝6，n＝．　　　 　　②MF过M（2，2）和F1（－4，－8），设MF为， 　　则　　解得，　∴　直线MF的解析式为． 　　直线MF与x轴交点为（，0），与y轴交点为（0，）． 　　若MP过点F（－4，－8），则n＝4－（）＝，m＝； 　　若MQ过点F（－4，－8），则m＝4－＝，n＝．　　 　故当　　或时，∠PMQ的边过点F．‎ ‎★★34、（2010南平）如图1，在△ABC中，AB=BC，P为AB边上一点，连接CP，以PA、PC为邻边作□APCD，AC与PD相交于点E，已知∠ABC=∠AEP=α（0°<α<90°）.‎ ‎（1）求证：∠EAP=∠EPA；‎ ‎（2）□APCD是否为矩形？请说明理由；‎ ‎（3）如图2，F为BC中点，连接FP，将∠AEP绕点E顺时针旋转适当的角度，得到∠MEN（点M、N分别是∠MEN的两边与BA、FP延长线的交点）.猜想线段EM与EN之间的数量关系，并证明你的结论.‎ 图1‎ A B D C E P 图2‎ A B D C E P M N F 解：(1)证明：在ΔABC和ΔAEP中，∵∠ABC=∠AEP，∠BAC=∠EAP ‎∴ ∠ACB=∠APE，在ΔABC中，AB=BC，∴∠ACB=∠BAC，∴ ∠EPA=∠EAP (2) 答：□ APCD是矩形 ‎∵四边形APCD是平行四边形，∴ AC=2EA, PD=2EP ‎∵ 由（1）知 ∠EPA=∠EAP，∴ EA=EP，则 AC=PD，∴□APCD是矩形 (3) 答： EM=EN， ∵EA=EP ∴ ∠EPA=90°－ α ‎∴∠EAM=180°-∠EPA=180°-(90°- α)=90°+ α 由（2）知∠CPB=90°,F是BC的中点，∴ FP=FB，∴∠FPB=∠ABC=α ‎∴ ∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°- α+α=90°+α ‎∴ ∠EAM=∠EPN ‎∵ ∠AEP绕点E顺时针旋转适当的角度，得到∠MEN，∴ ∠AEP=∠MEN ‎ ‎∴∠AEP- ∠AEN=∠MEN-∠AEN 即 ∠MEA=∠NEP ‎∴ ΔEAM≌ΔEPN ∴ EM=EN ‎★★35、（2010南平）26.(14分)如图1，已知点B（1，3）、C（1，0），直线y=x+k经过点B，且与x轴交于点A，将△ABC沿直线AB折叠得到△ABD.‎ ‎（1）填空：A点坐标为（____，____），D点坐标为（____，____）；‎ ‎（2）若抛物线y= x2+bx+c经过C、D两点，求抛物线的解析式；‎ ‎（3）将（2）中的抛物线沿y轴向上平移，设平移后所得抛物线与y轴交点为E，点M是平移后的抛物线与直线AB的公共点，在抛物线平移过程中是否存在某一位置使得直线EM∥x轴.若存在，此时抛物线向上平移了几个单位？若不存在，请说明理由.‎ ‎（提示：抛物线y=ax2+bx+c(a≠0)的对称轴是x=－，顶点坐标是（－，）‎ O y x A D B C 图1‎ O y x A B C 备用图 ‎·‎ 解：（1） A(-2，0) ，D(-2，3)‎ ‎ (2)∵抛物线y= x2+bx+c 经过C(1，0)，D(-2，3)‎ ‎ 代入，解得：b=- ,c= ‎ ‎∴ 所求抛物线解析式为：y= x2 － x+ （3） 答：存在 解法一： 设抛物线向上平移H个单位能使EM∥x轴，‎ 则平移后的解析式为：y= x2 － x++h =(x -1)² + h 此时抛物线与y轴交点E(0， +h)‎ 当点M在直线y=x+2上，且满足直线EM∥x轴时 则点M的坐标为（）‎ 又 ∵M在平移后的抛物线上，则有 ‎ +h=(h--1)²+h，解得： h= 或 h=‎ ‎（і）当 h= 时，点E（0，2），点M的坐标为（0，2）此时，点E,M重合，不合题意舍去。‎ ‎（ii）当 h=时，E（0，4）点M的坐标为（2，4）符合题意 综合（i）（ii）可知，抛物线向上平移个单位能使EM∥x轴。‎ 解法二：∵当点M在抛物线对称轴的左侧或在抛物线的顶点时，仅当M,E重合时，它们的纵坐标相等。∴EM不会与x轴平行 当点M在抛物线的右侧时，设抛物线向上平移H个单位能使EM∥x轴。‎ 则平移后的抛物线的解析式为∵y=x²++h =(x - 1)² + h ‎∴ 抛物线与Y轴交点E(0，+h)，∵抛物线的对称轴为：x=1‎ 根据抛物线的对称性，可知点M的坐标为（2，+h)时，直线EM∥x轴 将（2，+h)代入y=x+2得，+h=2+2 解得：h=‎ ‎∴ 抛物线向上平移个单位能使EM∥x轴。‎ ‎★★36、（2010宁德）如图，在梯形ABCD中，AD∥BC，∠B＝90°，BC＝6，AD＝3，∠DCB＝30°.点E、F同时从B点出发，沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍，以EF为一边在CB的上方作等边△EFG．设E点移动距离为x（x＞0）.‎ ‎⑴△EFG的边长是____（用含有x的代数式表示），当x＝2时，点G的位置在_______；‎ ‎⑵若△EFG与梯形ABCD重叠部分面积是y，求 ‎①当0＜x≤2时，y与x之间的函数关系式；‎ ‎②当2＜x≤6时，y与x之间的函数关系式；‎ B E→ F→ C A D G ‎⑶探求⑵中得到的函数y在x取含何值时，存在最大值，并求出最大值.‎ 解：⑴ x，D点； ‎ ‎⑵ ①当0＜x≤2时，△EFG在梯形ABCD内部，所以y＝x2；‎ ‎②分两种情况：‎ Ⅰ.当2＜x＜3时，如图1，点E、点F在线段BC上，‎ ‎△EFG与梯形ABCD重叠部分为四边形EFNM，‎ ‎∵∠FNC＝∠FCN＝30°,∴FN＝FC＝6－2x.∴GN＝3x－6.‎ 由于在Rt△NMG中，∠G＝60°，‎ 所以，此时 y＝x2－（3x－6）2＝. ‎ Ⅱ.当3≤x≤6时，如图2，点E在线段BC上，点F在射线CH上，‎ ‎△EFG与梯形ABCD重叠部分为△ECP，‎ ‎∵EC＝6－x,‎ ‎∴y＝（6－x）2＝.‎ ‎⑶当0＜x≤2时，∵y＝x2在x＞0时，y随x增大而增大，‎ ‎∴x＝2时，y最大＝；‎ 当2＜x＜3时，∵y＝，‎ 在x＝时，y最大＝；‎ 当3≤x≤6时，∵y＝，‎ 在x＜6时，y随x增大而减小，‎ ‎∴x＝3时，y最大＝.B E C F A D G P H 图2‎ 综上所述：当x＝时，y最大＝. ‎ B E F C A D G N M 图1‎ ‎★★37、（2010青岛）已知：把Rt△ABC和Rt△DEF按如图（1）摆放（点C与点E重合），点B、C（E）、F在同一条直线上．∠ACB = ∠EDF = 90°，∠DEF = 45°，AC = ‎8 cm，BC = ‎6 cm，EF = ‎9 cm．‎ 如图（2），△DEF从图（1）的位置出发，以‎1 cm/s的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△ABC的顶点B出发，以‎2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时，△DEF停止移动，点P也随之停止移动．DE与AC相交于点Q，连接PQ，设移动时间为t（s）（0＜t＜4.5）．解答下列问题：‎ ‎（1）当t为何值时，点A在线段PQ的垂直平分线上？‎ ‎（2）连接PE，设四边形APEC的面积为y（cm2），求y与t之间的函数关系式；是否存在某一时刻t，使面积y最小？若存在，求出y的最小值；若不存在，说明理由．‎ A D B C F ‎（‎ E ‎）‎ 图（1）‎ A D B C F E 图（2）‎ P Q ‎（3）是否存在某一时刻t，使P、Q、F三点在同一条直线上？若存在，求出此时t的值；若不存在，说明理由．（图（3）供同学们做题使用）‎ 解：（1）∵点A在线段PQ的垂直平分线上，∴AP = AQ.‎ 图（2）‎ Q A D B C F E P M ‎ ∵∠DEF = 45°，∠ACB = 90°，∠DEF＋∠ACB＋∠EQC = 180°，‎ ‎∴∠EQC = 45°. ∴∠DEF =∠EQC. ∴CE = CQ. ‎ ‎ 由题意知：CE = t，BP =2 t，∴CQ = t.，∴AQ = 8－t.‎ ‎ 在Rt△ABC中，由勾股定理得：AB = ‎10 cm .则AP = 10－2 t.‎ ‎ ∴10－2 t = 8－t. 解得：t = 2.‎ ‎ 答：当t = 2 s时，点A在线段PQ的垂直平分线上. ‎ ‎（2）过P作，交BE于M，∴.‎ 在Rt△ABC和Rt△BPM中，，‎ ‎ ∴ . ∴PM = . ∵BC = ‎6 cm，CE = t， ∴ BE = 6－t.‎ ‎ ∴y = S△ABC－S△BPE =－= －‎ ‎= = .‎ ‎∵，∴抛物线开口向上.∴当t = 3时，y最小=.‎ 答：当t = 3s时，四边形APEC的面积最小，最小面积为cm2. ‎ ‎（3）假设存在某一时刻t，使点P、Q、F三点在同一条直线上.过P作，交AC于N，∴.‎ C E A D B F 图（3）‎ P Q N ‎∵，∴△PAN ∽△BAC.‎ ‎∴.∴.‎ ‎∴，.∵NQ = AQ－AN，‎ ‎∴NQ = 8－t－() = ．‎ ‎∵∠ACB = 90°，B、C（E）、F在同一条直线上，‎ ‎∴∠QCF = 90°，∠QCF = ∠PNQ. ∵∠FQC = ∠PQN，∴△QCF∽△QNP .‎ ‎∴ . ∴ . ∵ ∴，解得：t = 1.‎ 答：当t = 1s，点P、Q、F三点在同一条直线上。 ‎ ‎★★38、（2010衢州）O y x C B A ‎1‎ ‎1‎ ‎-1‎ ‎-1‎ △ABC中，∠A=∠B=30°，AB=．把△ABC放在平面直角坐标系中，使AB的中点位于坐标原点O(如图)，△ABC可以绕点O作任意角度的旋转．‎ ‎(1)　当点B在第一象限，纵坐标是时，求点B的横坐标；‎ ‎(2)　如果抛物线(a≠0)的对称轴经过点C，请你探究：‎ ‎①　当，，时，A，B两点是否都在这条抛物线上？并说明理由；‎ ‎②　设b=-2am，是否存在这样的m的值，使A，B两点不可能同时在这条抛物线上？若存在，直接写出m的值；若不存在，请说明理由．‎ 解：(1)　 ∵　点O是AB的中点，　∴　． ‎ 设点B的横坐标是x(x>0)，则， ‎ 解得　，(舍去)． ∴　点B的横坐标是． ‎ ‎(2)　①　当，，时，得　　……(＊)‎ ‎． ‎ 以下分两种情况讨论．‎ 情况1：设点C在第一象限(如图甲)，则点C的横坐标为，‎ O y x C B A ‎(甲)‎ ‎1‎ ‎1‎ ‎-1‎ ‎-1‎ ‎． ‎ 由此，可求得点C的坐标为(，)， ‎ 点A的坐标为(，)，‎ ‎∵　A，B两点关于原点对称，‎ O y x C B A ‎(乙)‎ ‎1‎ ‎1‎ ‎-1‎ ‎-1‎ ‎∴　点B的坐标为(，)．‎ 将点A的横坐标代入(＊)式右边，计算得，即等于点A的纵坐标；‎ 将点B的横坐标代入(＊)式右边，计算得，即等于点B的纵坐标．‎ ‎∴　在这种情况下，A，B两点都在抛物线上． 　‎ 情况2：设点C在第四象限(如图乙)，则点C的坐标为(，-)，‎ 点A的坐标为(，)，点B的坐标为(，)．‎ 经计算，A，B两点都不在这条抛物线上． 　 　‎ ‎(情况2另解：经判断，如果A，B两点都在这条抛物线上，那么抛物线将开口向下，而已知的抛物线开口向上．所以A，B两点不可能都在这条抛物线上)‎ ‎②　存在．m的值是1或-1． 　‎ ‎(，因为这条抛物线的对称轴经过点C，所以-1≤m≤1．当m=±1时，点C在x轴上，此时A，B两点都在y轴上．因此当m=±1时，A，B两点不可能同时在这条抛物线上)‎ ‎★★39、（2010日照）如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC与E，交BC与D．求证：‎ ‎（1）D是BC的中点； ‎ ‎（2）△BEC∽△ADC；‎ ‎（3）BC2=2AB·CE．‎ 解：（1）证明：∵AB是⊙O的直径，∴∠ADB=90° ，‎ 即AD是底边BC上的高．又∵AB=AC，∴△ABC是等腰三角形， ‎ ‎∴D是BC的中点；‎ ‎ (2) 证明：∵∠CBE与∠CAD是同弧所对的圆周角，‎ ‎ ∴ ∠CBE=∠CAD． 又∵ ∠BCE=∠ACD， ∴△BEC∽△ADC；‎ ‎（3）证明：由△BEC∽△ADC，知，‎ 即CD·BC=AC·CE． ∵D是BC的中点，∴CD=BC． ‎ ‎ 又 ∵AB=AC，∴CD·BC=AC·CE=BC ·BC=AB·CE 即BC=2AB·CE．‎ ‎★★40、（2010绍兴）如图,设抛物线C1:, C2:,C1与C2的交点为A, B,点A的坐标是,点B的横坐标是－2.‎ ‎ （1）求的值及点B的坐标； ‎ ‎（2）点D在线段AB上,过D作x轴的垂线,垂足为点H,‎ 在DH的右侧作正三角形DHG. 记过C2顶点Ｍ的 直线为,且与x轴交于点N.‎ ‎① 若过△DHG的顶点G,点D的坐标为 ‎(1, 2)，求点N的横坐标；‎ ‎② 若与△DHG的边DG相交,求点N的横 坐标的取值范围.‎ 解：（1）∵ 点A在抛物线C1上，∴ 把点A坐标代入得 =1. ‎ 图1‎ ‎∴ 抛物线C1的解析式为,‎ ‎ 设B(－2,b)， ∴ b＝－4, ∴ B(－2,－4) . ‎ ‎（2）①如图1，‎ ‎∵ M(1, 5)，D(1, 2), 且DH⊥x轴，‎ ‎∴ 点M在DH上，MH=5. ‎ 过点G作GE⊥DH,垂足为E,‎ 由△DHG是正三角形,可得EG=, EH=1，‎ ‎∴ ME＝4. ‎ 图2‎ 设N ( x, 0 ), 则 NH＝x－1,‎ 由△MEG∽△MHN,得 ,‎ ‎∴ , ∴ ,‎ ‎∴ 点N的横坐标为． ‎ ‎② 当点Ｄ移到与点A重合时,如图2，‎ 直线与DG交于点G,此时点Ｎ的横坐标最大．‎ 图3‎ 图4‎ 过点Ｇ,Ｍ作x轴的垂线,垂足分别为点Ｑ,F,‎ 设Ｎ（x，0），‎ ‎∵ A (2, 4), ∴ G (, 2),‎ ‎∴ NQ=，ＮF =, GQ=2, MF =5.‎ ‎∵ △NGQ∽△NMF，‎ ‎∴ ,‎ ‎∴ ,‎ ‎∴ . ‎ 当点D移到与点B重合时,如图3，‎ 直线与DG交于点D,即点B，此时点N的横坐标最小.‎ ‎ ∵ B(－2, －4), ∴ H(－2, 0), D(－2, －4),‎ 设N（x，0）， ‎ ‎∵ △BHN∽△MFN， ∴ ，‎ ‎∴ , ∴ . ‎ ‎∴ 点N横坐标的范围为 ≤x≤. ‎ ‎　记住，永远不要对父母说这十句话！‎ ‎　　1.好了，好了，知道，真啰嗦！（可怜天下父母心，父母的“啰嗦”其实是一种幸福。）‎ ‎　　2.有事吗，没事？那挂了啊。（父母打电话，也许只想说说话，我们能否明白他们的用意，不要匆忙挂了电话！）‎ ‎　　3.说了你也不懂，别问了！（他们只是想和我们说说话。）‎ ‎　　4.跟你说了多少次不要你做，做又做不好。（一些他们已经力不能及的事，我们因为关心而制止，但不要这样让他们觉得自己很无用。）‎ ‎　　5.你们那一套，早就过时了。（父母的建议，也许不能起到作用，可我们是否能换一种回应的方式？）‎ ‎　　6.叫你别收拾我的房间，你看，东西找都找不到！（自己的房间还是自己收拾好，不收拾，也不要拂了老人的好意。）‎ ‎　　7.我要吃什么我知道，别夹了！（盼着我们回家的父母总想把所有关心融在特意做的菜里，我们默默领情就好。）‎ ‎　　8.说了别吃这些剩菜了，怎么老不听啊！（他们一辈子的节约习惯，很难改，让他们每次尽量少做点菜就好。）‎ ‎　　9.我自己有分寸，不要老说了，烦不烦。（他们只是担心你吃亏。）‎ ‎　　10.这些东西说了不要了，堆在这里做什么啊！（人老了都会念旧……）‎ ‎　　当你还在襁褓时，她便天天抱着你，哄你入睡；当你到少年时代，她便天天念叨着你，夜夜帮你捻着棉被；当你终于离开家，远行他方，她便天天牵挂着你。‎ ‎　　有时候，我们总是在抱怨母亲的唠叨、念叨，总是在心烦她那些说了无数遍的关心话语。都说儿女是父母前辈子欠下的债，这句话不假。让我们感恩于心，让我们感恩父母那些点滴的关怀。‎ ‎　　如果有一天，你发现母亲煮的菜太咸太难吃，如果有一天，你发现父母经常忘记关电器；‎ ‎　　如果有一天，你发现父亲的花草树木已渐荒废，如果有一天，你发现家中的地板衣柜经常沾满灰尘；‎ ‎　　如果有一天，你发现父母不再爱吃青脆的蔬果，如果有一天，你发现父母爱吃煮得烂烂的菜；‎ ‎　　如果有一天，你发现吃饭时间他们老是咳个不停，千万别误以为他们感冒或着凉（那是吞咽神经老化的现象）；‎ ‎　　如果有一天，你发觉他们不再爱出门……也许是因为身体一天不如一天……‎ ‎　　每个人都会老，父母会比我们先老。当父母不能照顾自己的时候，很多事情做得不好的时候，请不要嫌弃他们，并请维持他们的“自尊心”.‎ ‎　　当他们不爱洗澡时，请抽空定期帮他们洗身体，因为纵使他们自己洗也不可能洗干净；‎ ‎　　当我们享受美食的时候，请替他们准备大小适当、容易咀嚼的一小碗。他们不爱吃，可能是因为牙齿咬不动了。‎ ‎　　曾经听到过这样一个说法：其实，每位母亲都是一位漂亮的仙女，她们有一件非常美丽的衣裳。可是当她决定做某个孩子母亲的时候，当她准备呵护某个生命的时候，就会褪去这件美丽的衣裳，变成一名普通的女子，一辈子，平淡无奇。‎