湖北武汉市江岸区中考数学模拟试卷含答案 10页

‎2019年 中考数学模拟试卷 一、选择题 有四包真空包装的火腿肠,每包以标准质量450g为基准,超过的克数记作正数，,不足的克数记作负数.下面的数据是记录结果,其中与标准质量最接近的是（ ）‎ A.+2 B.﹣3 C.+4 D.﹣1‎ 在函数中，自变量x的取值范围是（ ）‎ A.x＜ B.x≠﹣ C.x≠ D.x＞‎ 若﹣x3ya与xby是同类项,则a+b的值为（ ）‎ A.2 B.3 C.4 D.5‎ 某商场一天中售出李宁牌运动鞋11双，其中各种尺码的鞋的销售量如下表所示，‎ 鞋的尺码（单位：厘米）‎ ‎23.5‎ ‎24‎ ‎24.5‎ ‎25‎ ‎26‎ 销售量（单位：双）‎ ‎1‎ ‎2‎ ‎2‎ ‎5‎ ‎1‎ 则这11双鞋的尺码组成一组数据中众数和中位数分别为（ ）‎ A.25，25 B.24.5，25 C.26，25 D.25，24.5‎ 若(x＋3)(x＋m)=x2-2x-15，则 m 的值为(    )‎ A.5         B.-5       C.2            D.-2‎ 若点P在第二象限，且到x轴的距离为3，到y轴的距离为4，则点P的坐标为(　　)‎ A.(3，4) B.(-3，4) C.(-4，3) D.(4，3)‎ 如图,是由几个相同的小正方体组成的一个几何体的三视图,这个几何体可能是（ ）‎ ‎ A. B. C. D.‎ 如图，在2×2网格中放置了三枚棋子，在其他格点处再放置1枚棋子，使图形中的四枚棋子成为轴对称图形的概率是（ ）‎ ‎ A. B. C. D. 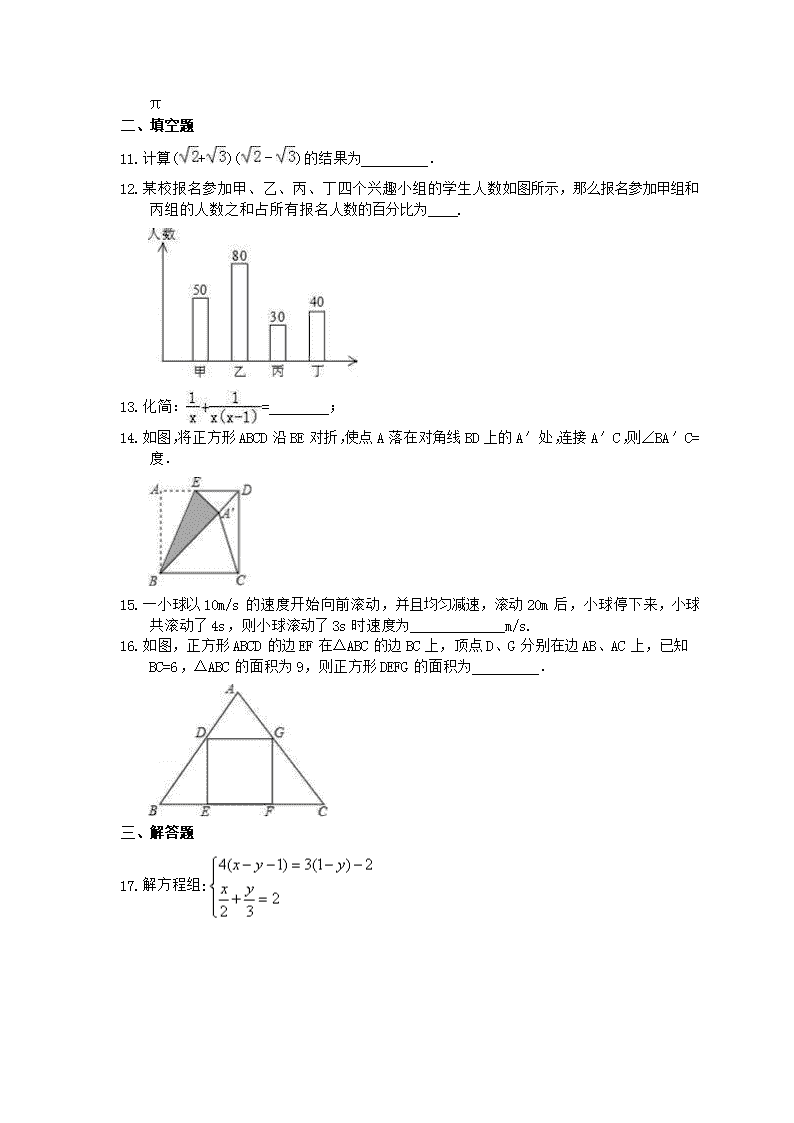‎ 某商贩在一次买卖中，同时卖出两件上衣，每件都以80元出售，若按成本计算，其中一件赢利60%，另一件亏本20%，在这次买卖中，该商贩（　　）‎ A.不盈不亏 B.盈利10元 C.亏损10元 D.盈利50元 如图，在Rt△ABC中，∠ACB=90°，∠BAC=60°．把△ABC绕点A按顺时针方向旋转60°后得到△AB/C/，若AB=4，则线段BC在上述旋转过程中所扫过部分（阴影部分）的面积是（ ）‎ ‎ A.π B.π C.2π D.4‎ π 二、填空题 计算(+)(﹣)的结果为 ．‎ 某校报名参加甲、乙、丙、丁四个兴趣小组的学生人数如图所示，那么报名参加甲组和丙组的人数之和占所有报名人数的百分比为　　.‎ 化简：=　　 ；‎ 如图，将正方形ABCD沿BE对折，使点A落在对角线BD上的A′处，连接A′C，则∠BA′C=　　　　度．‎ 一小球以10m/s的速度开始向前滚动，并且均匀减速，滚动20m后，小球停下来，小球共滚动了4s，则小球滚动了3s时速度为       m/s.‎ 如图，正方形ABCD的边EF在△ABC的边BC上，顶点D、G分别在边AB、AC上，已知BC=6，△ABC的面积为9，则正方形DEFG的面积为　　 ．‎ 三、解答题 解方程组:‎ 已知：如图AC，BD相交于点O，∠A=∠D，AB=CD，求证：△AOB≌△DOC．‎ 某校为了更好的开展“学校特色体育教育”，从全校八年级的各班分别随机抽取了5名男生和5名女生，组成了一个容量为60的样本，进行各项体育项目的测试，了解他们的身体素质情况.下表是整理样本数据，得到的关于每个个体的测试成绩的部分统计表、图：某校60名学生体育测试成绩频数分布表 ‎（说明：40﹣﹣﹣55分为不合格，55﹣﹣﹣70分为合格，70﹣﹣﹣85分为良好，85﹣﹣﹣100分为优秀）请根据以上信息，解答下列问题：‎ ‎（1）表中的a=　　　　　　，b=　　　　　　；‎ ‎（2）请根据频数分布表，画出相应的频数分布直方图；‎ ‎（3）如果该校八年级共有150名学生，根据以上数据，估计该校八年级学生身体素质良好及以上的人数为　　　　　　.‎ 国庆期间，为了满足百姓的消费需求，某商店计划用170000元购进一批家电，这批家电的进价和售价如表：‎ 类别 彩电 冰箱 洗衣机 进价（元/台） 2000 1600 1000‎ 售价（元/台） 2300 1800 1100‎ 若在现有资金允许的范围内，购买表中三类家电共100台，其中彩电台数是冰箱台数的2倍，设该商店购买冰箱x台．‎ ‎（1）商店至多可以购买冰箱多少台？‎ ‎（2）购买冰箱多少台时，能使商店销售完这批家电后获得的利润最大？最大利润为多少元？‎ 如图，在△ABC中，AB=AC，∠BAC=54°，以AB为直径的⊙O分别交AC，BC于点D，E，过点B作⊙O的切线，交AC的延长线于点F．‎ ‎（1）求证：BE=CE；（2）求∠CBF的度数；（3）若AB=6，求的长．‎ 如图，四边形OABC是面积为4的正方形，函数y=kx-1(x>0)的图象经过点B.‎ ‎(1) 求k的值；‎ ‎（2）将正方形OABC分别沿直线AB，BC翻折，得到正方形MABC′和NA′BC.设线段MC′，NA′分别与函数y=kx-1(x>0)的图象交于点F，E. 求线段EF所在直线的解析式.‎ ‎ ‎ 如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点，然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC（结果精确到1m）．‎ 如图，二次函数y=ax2+bx+3的图象与x轴相交于点A（﹣3，0）、B（1，0），与y轴相交于点C，点G是二次函数图象的顶点，直线GC交x轴于点H（3，0），AD平行GC交y轴于点D．‎ ‎（1）求该二次函数的表达式；‎ ‎（2）求证：四边形ACHD是正方形；‎ ‎（3）如图2，点M（t，p）是该二次函数图象上的动点，并且点M在第二象限内，过点M的直线y=kx交二次函数的图象于另一点N．‎ ‎①若四边形ADCM的面积为S，请求出S关于t的函数表达式，并写出t的取值范围；‎ ‎②若△CMN的面积等于，请求出此时①中S的值．‎ 答案 D C C.‎ A B ‎ C；‎ B C B C 答案为：﹣1．‎ 答案为：286；‎ 答案为：；‎ 答案为：67.5．‎ 答案为：2.5； ‎ 答案为：4．‎ 答案为:x=2,y=3.‎ 证明：在△AOB和△DOC中，，所以，△AOB≌△DOC（AAS）．‎ 解：（1）60×30%=18，30÷60×100%=50%，∴a=18，b=50%；‎ ‎（2）如图，‎ ‎（3）150×（30%+50%）=120.‎ （1）证明：连接AE，∵AB是⊙O直径，∴∠AEB=90°，即AE⊥BC，∵AB=AC，∴BE=CE．‎ ‎（2）解：∵∠BAC=54°，AB=AC，∴∠ABC=63°，‎ ‎∵BF是⊙O切线，∴∠ABF=90°，∴∠CBF=∠ABF﹣∠ABC=27°．‎ ‎（3）解：连接OD，∵OA=OD，∠BAC=54°，∴∠AOD=72°，‎ ‎∵AB=6，∴OA=3，∴弧AD的长是=．‎ 解：(1) ∵ B（2,2），∴ k= 4 ‎ ‎(2) 由翻折可知，M（4,0）N（0,4）可求得F（4,1），E（1,4）‎ 设直线EF的解析式为y=kx+b，可求得k=-1,b=5.所以，线段EF所在直线的解析式为y=-x+5.‎ 解：过点D作DE⊥AC于点E，过点D作DF⊥BC于点F，‎ 由题意可得：∠ADE=15°，∠BDF=15°，AD=1600m，AC=500m，‎ ‎∴cos∠ADE=cos15°=≈0.97，∴≈0.97，解得：DE=1552（m），‎ sin15°=≈0.26，∴≈0.26，解得；AE=416（m），‎ ‎∴DF=500﹣416=84（m），∴tan∠BDF=tan15°=≈0.27，∴≈0.27，‎ 解得：BF=22.68（m），∴BC=CF+BF=1552+22.68=1574.68≈1575（m），‎ 答：他飞行的水平距离为1575m．‎ 解：‎ ‎ ‎ ‎ ‎