初中中考复习之圆锥和扇形的计算精编含答案 9页

中考复习之圆锥和扇形的计算 一、选择题：‎ ‎1.如图是某公园的一角，∠AOB=90°，弧AB的半径OA长是‎6米，C是OA的中点，点D在弧AB上，CD∥OB，则图中休闲区（阴影部分）的面积是【 】‎ A．米2 B．米‎2 ‎C．米2D．米2‎ ‎2.如图，一根‎5m长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊A(羊只能在草地上活动)，那么小羊A在草地上的最大活动区域面积是【 】‎ ‎ A.πm2 B.πm‎2 C.πm2 D.πm2‎ ‎3.一个扇形的圆心角为60°，它所对的弧长为2πcm，则这个扇形的半径为【 】‎ A．‎6cm B．‎12cm C．‎2‎cm D．cm ‎4.如果一个扇形的半径是1，弧长是，那么此扇形的圆心角的大小为【 】‎ A. 30° B. 45° C ．60° D．90°‎ ‎5.已知一个圆锥的底面半径为‎3cm，母线长为‎10cm，则这个圆锥的侧面积为（　　）‎ ‎　A． 15πcm2 B． 30πcm2 C． 60πcm2 D． 3cm2‎ ‎6.用圆心角为120°，半径为‎6cm的扇形纸片卷成一个圆锥形无底纸帽（如图所示），则这个纸帽的高是【 】‎ ‎　　A．cm　　B．3cm　　C．4cm　　D．‎‎4cm ‎7.如图，扇形DOE的半径为3，边长为的菱形OABC的顶点A，C，B分别在OD，OE，弧DE上，若把扇形DOE围成一个圆锥，则此圆锥的高为【 】‎ ‎　A． B． C． D． ‎ ‎8.用半径为‎2cm的半圆围成一个圆锥的侧面，这个圆锥的底面半径为【 】‎ A．‎1cm B．‎2cm C．πcm D．2πcm ‎9.已知圆锥的底面半径为‎3cm，母线长为‎5cm，则圆锥的侧面积是【 】‎ ‎　A． 20cm2 B． 20πcm2 C． 15cm2 D． 15πcm2‎ ‎10.如图，一枚直径为‎4cm的圆形古钱币沿着直线滚动一周，圆心移动的距离是【 】‎ A．‎2‎cm B．‎4‎cm C．‎8‎cm D．‎16‎cm ‎11.如图所示，扇形AOB的圆心角为120°，半径为2，则图中阴影部分的面积为【 】‎ A. B. C. D. ‎ ‎12.如图，在Rt△ABC中，∠C=90°，∠A=30°，AC=‎6cm，CD⊥AB于D，以C为圆心，CD为半径画弧，交BC于E，则图中阴影部分的面积为【 】‎ A．cm2 B．cm‎2 C．cm2 D．cm2‎ ‎13.如图，⊙O的外切正六边形ABCDEF的边长为2，则图中阴影部分的面积为【 】．‎ A． B． C． D． ‎14.如图，正方形MNEF的四个顶点在直径为4的大圆上，小圆与正方形各边都相切，AB与CD是大圆的直径，AB⊥CD，CD⊥MN，则图中阴影部分的面积是【 】‎ ‎　A． 4π B． 3π C． 2π D． π ‎15.如图，圆锥形冰淇淋盒的母线长是‎13cm，高是‎12cm，则该圆锥形底面圆的面积是【 】‎ ‎　A．10πcm2 B．25πcm2 C．60πcm2 D．65πcm2‎ ‎16.一个圆锥的侧面积是底面积的2倍。则圆锥侧面展开图的扇形的圆心角是【 】‎ A .1200 B‎.1800 ‎‎ C.2400 D.3000‎ ‎17.如图，在Rt△ABC中，∠ACB=90°，∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB＇C ＇，若AB=4，则线段BC在上述旋转过程中所扫过部分（阴影部分）的面积是【 】‎ A. π B. π C. 2π D. 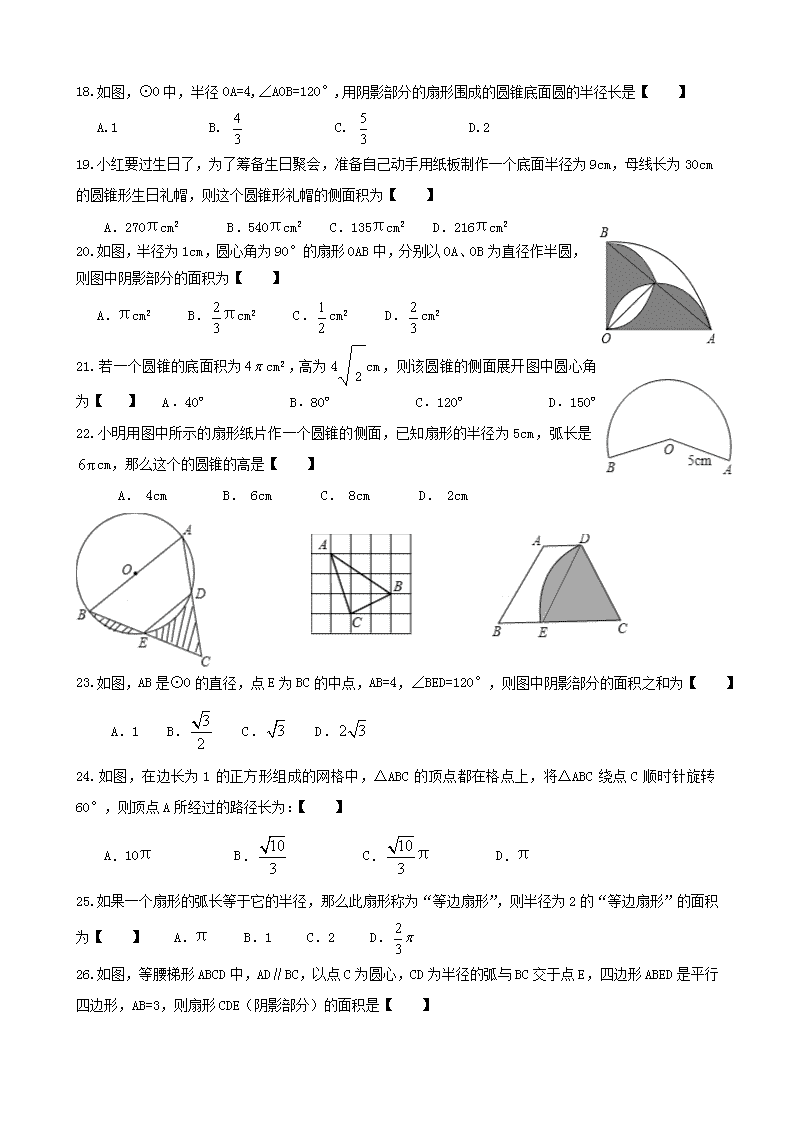4π ‎18.如图，⊙O中，半径OA=4,∠AOB=120°,用阴影部分的扇形围成的圆锥底面圆的半径长是【 】‎ A.1 B. C. D.2‎ ‎19.小红要过生日了，为了筹备生日聚会，准备自己动手用纸板制作一个底面半径为‎9cm，母线长为‎30cm的圆锥形生日礼帽，则这个圆锥形礼帽的侧面积为【 】‎ ‎　　A．270πcm2　　 B．540πcm‎2　‎　C．135πcm2　　D．216πcm2‎ ‎20.如图，半径为‎1cm，圆心角为90°的扇形OAB中，分别以OA、OB为直径作半圆，则图中阴影部分的面积为【 】‎ A．πcm2 B．πcm‎2 C．cm2 D．cm2‎ ‎21.若一个圆锥的底面积为cm2，高为‎4cm，则该圆锥的侧面展开图中圆心角为【 】 A．40º B．80º C．120º D．150º ‎22.小明用图中所示的扇形纸片作一个圆锥的侧面，已知扇形的半径为‎5cm，弧长是cm，那么这个的圆锥的高是【 】‎ A． ‎4cm B． ‎6cm C． ‎8cm D． ‎‎2cm ‎23.如图，AB是⊙O的直径，点E为BC的中点，AB=4，∠BED=120°，则图中阴影部分的面积之和为【 】A．1　　B．　　C．　　D．‎ ‎24.如图，在边长为1的正方形组成的网格中，△ABC的顶点都在格点上，将△ABC绕点C顺时针旋转60°，则顶点A所经过的路径长为：【 】‎ A．10π B． C．π D．π ‎25.如果一个扇形的弧长等于它的半径，那么此扇形称为“等边扇形”，则半径为2的“等边扇形”的面积为【 】 A．π B．‎1 ‎‎ C．2 D．‎ ‎26.如图，等腰梯形ABCD中，AD∥BC，以点C为圆心，CD为半径的弧与BC交于点E，四边形ABED是平行四边形，AB=3，则扇形CDE（阴影部分）的面积是【 】‎ A． B． C．π D．3π ‎27.‎ ‎28.如图，在△ABC中，BC=4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于点E， 交AC于点F，点P是OA上的一点，且∠EPF=450，图中阴影影部分的面积为【 】‎ ‎ A．4一 B．4—‎2‎ C、8+ D．8-2‎ ‎29.如图，AB是⊙O的直径，弦CD⊥A，∠CDB=300，CD=，则阴影部分图形的面积为【 】‎ ‎ A. B. C. D.‎ 二、填空题：‎ ‎1.一个扇形的圆心角为120°，半径为3，则这个扇形的面积为 （结果保留）‎ ‎2.如图，在平行四边形ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是　 　（结果保留π）．‎ ‎3.扇形的半径是‎9 cm ，弧长是‎3pcm，则此扇形的圆心角为 度． ‎ ‎4.已知扇形的半径为‎3 cm，圆心角为1200，则此扇形的的弧长是 cm，扇形的面积是 cm2（结果保留π）。‎ ‎5.若圆锥的底面半径为‎2cm，母线长为‎5cm，则此圆锥的侧面积为 cm2。‎ ‎6.已知扇形的圆心角为45°，弧长等于，则该扇形的半径是 .‎ ‎7.如图，SO，SA分别是圆锥的高和母线，若SA=‎12cm，∠ASO=30°，则这个圆锥的侧面积是 cm2.(结果保留π)‎ ‎8.已知一个圆锥的母线长为‎10cm，将侧面展开后所得扇形的圆心角是144°，则这个圆锥的底面圆的半径是　 　cm．‎ ‎9.若圆锥的底面半径为3，母线长为6，则圆锥的侧面积等于 。‎ ‎10.若扇形的圆心角为60°，弧长为２，则扇形的半径为　　 　　．‎ ‎11.如图，从一个直径为4dm的圆形铁皮中剪出一个圆心角为60°的扇形ABC，并将剪下来的扇形围成一个圆锥，则圆锥的底面半径为　 　dm．‎ ‎12.圆锥底面半径为，母线长为2，它的侧面展开图的圆心角是　 　．‎ ‎13.在半径为‎1cm的圆中，圆心角为120°的扇形的弧长是　 　cm．‎ ‎14.已知圆锥的底面直径和母线长都是‎10cm，则圆锥的侧面积为 ．‎ ‎15.如图，已知圆O的半径为4，∠A=45°，若一个圆锥的侧面展开图与扇形OBC能完全重合，则该圆锥的底面圆的半径为　 　．‎ ‎16.圆锥底面圆的半径为‎3cm，母线长为‎9cm，则这个圆锥的侧面积为 ‎ cm2（结果保留π）．‎ ‎17.一个几何体由圆锥和圆柱组成，其尺寸如图所示，则该几何体的全面积(即表面积)为 (结果保留π)‎ ‎18.底面半径为1，高为的圆锥的侧面积等于 ．‎ ‎19.已知圆锥的底面半径为4，母线长为6，则它的侧面积是 .（不取近似值）‎ ‎20.如图，小正方形构成的网络中，半径为1的⊙O在格点上，则图中阴影部分两个小扇形的面积之和为 （结果保留）。‎ ‎21.有一个底面半径为‎3cm，母线长‎10cm的圆锥，则其侧面积是 cm2‎ ‎22.用一个圆心角为120°，半径为4的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径为 ‎ ‎23.已知圆锥的母线长为‎8cm，底面圆的半径为‎3cm，则圆锥的侧面展开图的面积是 cm2．‎ ‎24.如图，在正方形ABCD内有一折线，其中AE⊥EF，EF⊥FC，并且AE=4，EF=8，FC=12。则正方形与其外接圆形成的阴影部分的面积为 。‎ ‎25.如图，一个圆锥形零件，高为‎8cm，底面圆的直径为‎12cm，则 此圆锥的侧面积是 ．‎ ‎26.若一个圆锥的底面半径为3，母线长为4，则这个圆锥的侧面积为 ．‎ ‎27.已知扇形AOB中，若∠AOB=450，AD=‎4cm，弧CD的长为3πcm，则图中阴影部分的面积是　 　．‎ ‎28.已知圆锥的底面半径为‎10cm，它的展开图的扇形的半径为‎30cm，则这个扇形圆心角的度数是 。‎ ‎29.如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=2．将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置，B，A，C′三点共线，则线段BC扫过的区域面积为　 　．‎ ‎30.如图，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成．已知正三角形的边长为1，则凸轮的周长等于　 　．‎ ‎31.在半径为‎6cm的圆中，60°的圆心角所对的弧长等于　 　cm（结果保留π）．‎ ‎32.从纸上剪下一个圆和一个扇形的纸片（如图），圆的半径为2，扇形的圆心角等于1200.若用它们恰好围成一个圆锥模型，则此扇形的半径为 .‎ ‎33.如图，在△ABC中，∠A＝50°，BC＝6，以BC为直径的半圆O与AB、AC分别交于点D、E，则图中阴影部分的面积之和等于　　 　　（结果保留π）。‎ ‎34.已知扇形的圆心角为半径为，则该扇形的面积为 (结果保留).‎ ‎35.母线长为3，底面圆的直径为2的圆锥的侧面积为 ‎ ‎36.一条弧所对的圆心角为135º，弧长等于半径为‎5cm的圆的周长的3倍，则这条弧的半径为 cm．‎ ‎37.如图，在Rt△ABC中，∠C=90°，AC=4，BC=2，分别以AC、BC为直径画半圆，则图中阴影部分的面积为 （结果保留π）．‎ ‎38.如图是某几何体的三视图及相关数据（单位：cm），则该几何体的侧面积为　 　cm．‎ ‎39.小明同学用纸板制作了一个圆锥形漏斗模型．如图所示，它的底面半径OB=‎3cm，高OC=‎4cm，则这个圆锥漏斗的侧面积是 cm2．‎ ‎40.用半径为9，圆心角为1200的扇形围成一个圆锥，则圆锥的高为 ．‎ ‎41.圆锥的母线长为4，侧面积为8，则圆锥的底面圆的半径是 ．‎ ‎42.如图，菱形ABCD的边长为‎2cm，∠A=600。弧BD是 以点A为圆心、AB为半径的弧，弧CD是以点B为圆心、BC长为半径的弧。则阴影部分的面积为 cm2。‎ 三、解答题：‎ ‎1.如图所示为圆柱形大型储油罐固定在U型槽上的横截面图．已知图中ABCD为等腰梯形（AB∥DC），支点A与B相距‎8m，罐底最低点到地面CD距离为‎1m．设油罐横截面圆心为O，半径为‎5m，∠D=56°，求：U型槽的横截面（阴影部分）的面积．（参考数据：sin53°≈0.8，tan56°≈1.5，π≈3，结果保留整数）‎ ‎2.如图，实线部分为某月牙形公园的轮廓示意图，它可看作是由⊙P上的一段优弧和⊙Q上的一段劣弧围成，⊙P与⊙Q的半径都是‎2km，点P在⊙Q上．(1) 求月牙形公园的面积；‎ ‎(2) 现要在公园内建一块顶点都在⊙P上的直角三角形场地ABC，其中∠C=，求场地的最大面积．‎ ‎3.如图，在⊙O中，直径AB=2，CA切⊙O于A，BC交⊙O于D，若∠C=45°，则 ‎（1）BD的长是　 　； （2）求阴影部分的面积．‎ 一、选择题：‎ ‎1、C 2、D 3、A 4、C 5、B 6、C 7、D 8、A 9、D 10、B 11、A ‎12、A 13、A 14、D 15、B 16、B 17、C 18、B 19、A 20、C 21、C ‎22、A 23、C 24、C 25、C 26、A 27、C 28、A 29、D ‎ 二、填空题：‎ ‎1、 2、 3、60 4、， 5、10π 6、2 7、 8、4 9、‎ ‎10、6 11、1 12、900 13、 14、50πcm2 15、1 16、27π 17、68π ‎18、2π 19、24π 20、 21、30π 22、 23、24π 24、‎ ‎25、60πcm2 26、 27、cm2 28、120° 29、 30、π 31、‎ ‎32、6 33、 34、 35、3π 36、40 37、 38、2π 39、‎ ‎40、 41、2 42、‎ 三、解答题：‎ ‎1、解：如图，连接AO、BO．过点A作AE⊥DC于点E，过点O作ON⊥DC于点N，ON交⊙O于点M，交AB于点F．则OF⊥AB．‎ ‎∵OA=OB=‎5m，AB=‎8m，‎ ‎∴AF=BF=AB=4（m），∠AOB=2∠AOF，‎ 在Rt△AOF中，，‎ ‎∴∠AOF=53°，∴∠AOB=106°。‎ ‎∵（m），由题意得：MN=‎1m，∴FN=OM－OF+MN=3（m）。‎ ‎∵四边形ABCD是等腰梯形，AE⊥DC，FN⊥AB，∴AE=FN=‎3m，DC=AB+2DE。‎ 在Rt△ADE中，，∴DE=‎2m，DC=‎12m。‎ ‎∴（m2）。‎ 答：U型槽的横截面积约为‎20m2‎。‎ ‎2、【答案】解：（1）连接DQ、EQ、PD、PE、PQ、DE。‎ 由已知PD=PQ=DQ，∴△DPQ是等边三角形。‎ ‎∴∠DQP=60°。‎ 同理∠EQP=60°。 ∴∠DQE=120°。‎ ‎∵，‎ ‎，，∴。‎ ‎∴月牙形公园的面积=（km2）。‎ 答：月牙形公园的面积为km2。‎ ‎（2）∵∠C=90°，∴AB是⊙P的直径。‎ 过点C作CF⊥AB于点F，CF·AB，∵AB=4 km , ‎ ‎∴取最大值就是CF长度取最大值，即CF=‎2km。‎ ‎3、解：（1）。连接AD，‎ ‎∵AC是⊙O的切线，∴AB⊥AC。‎ ‎∵∠C=45°，∴AB=AC=2。∴。‎ ‎∵AB是⊙O的直径，∴∠ADB=90°。∴D是BC的中点。∴BD=BC=。‎ ‎（2）连接OD，AD，‎ ‎∵O是AB的中点，D是BC的中点，‎ ‎∴OD是△ABC的中位线。∴OD=1。‎ ‎∴OD⊥AB，∴。‎ ‎∴与弦BD组成的弓形的面积等于与弦AD组成的弓形的面积，‎ ‎∴ =AB•AC﹣AB•OD=×2×2﹣×2×1=2﹣1=1。‎