中考数学压轴题分类解析汇编十专题专题09 几何综合问题 31页

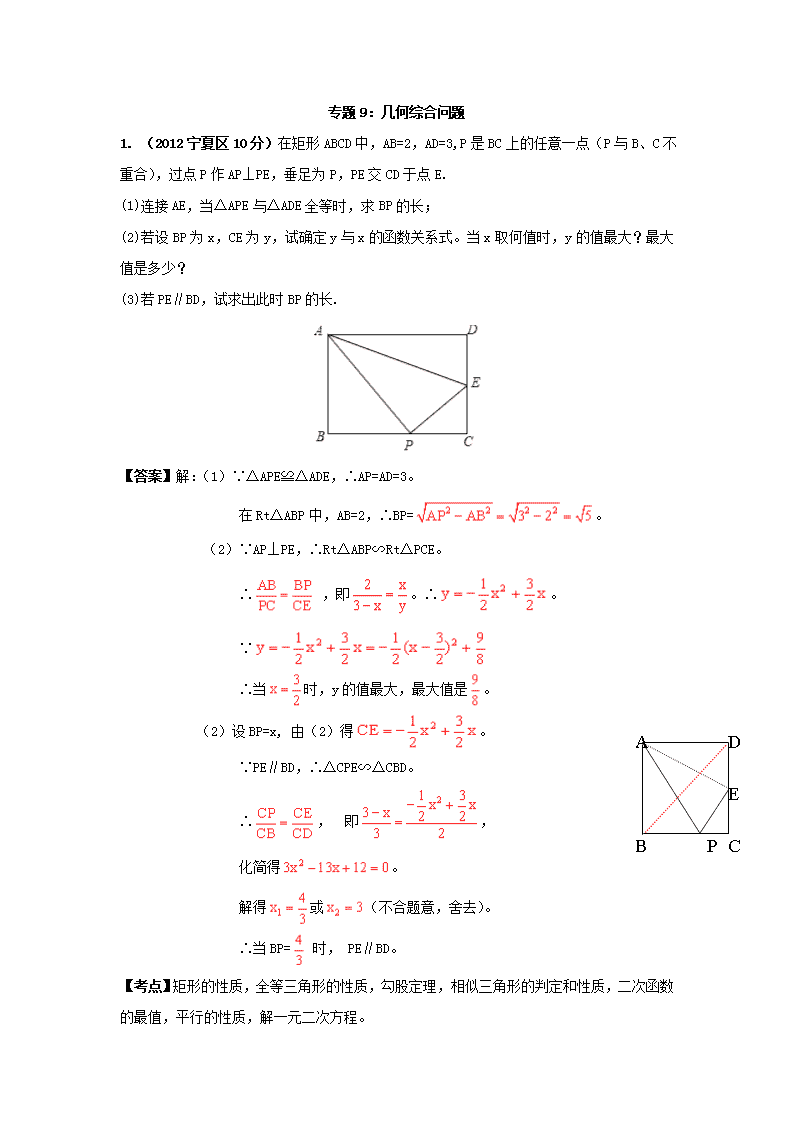
专题9：几何综合问题 ‎1. （2012宁夏区10分）在矩形ABCD中，AB=2，AD=3,P是BC上的任意一点（P与B、C不重合），过点P作AP⊥PE，垂足为P，PE交CD于点E.‎ ‎(1)连接AE，当△APE与△ADE全等时，求BP的长；‎ ‎(2)若设BP为x，CE为y，试确定y与x的函数关系式。当x取何值时，y的值最大？最大值是多少？‎ ‎(3)若PE∥BD，试求出此时BP的长.‎ ‎【答案】解：（1）∵△APE≌△ADE，∴AP=AD=3。‎ 在Rt△ABP中，AB=2，∴BP=。‎ ‎（2）∵AP⊥PE，∴Rt△ABP∽Rt△PCE。‎ ‎∴ ，即。∴。 ‎ ‎∵‎ ‎∴当时，y的值最大，最大值是。‎ ‎（2）设BP=x, 由（2）得。‎ ‎∵PE∥BD，∴△CPE∽△CBD。‎ ‎∴， 即，‎ 化简得。‎ 解得或（不合题意，舍去）。‎ ‎∴当BP= 时， PE∥BD。‎ ‎【考点】矩形的性质，全等三角形的性质，勾股定理，相似三角形的判定和性质，二次函数的最值，平行的性质，解一元二次方程。‎ ‎【分析】（1）由△APE≌△ADE可得AP=AD=3，在Rt△ABP中，应用勾股定理即可求得BP的长。‎ ‎（2）由AP⊥PE，得Rt△ABP∽Rt△PCE，根据相似三角形的对应边成比例可列式得y与x的函数关系式。化为顶点式即可求得当时，y的值最大，最大值是。‎ ‎（3）由PE∥BD，得△CPE∽△CBD，根据相似三角形的对应边成比例可列式可求得BP的长。‎ ‎2. （2012山西省12分）问题情境：将一副直角三角板（Rt△ABC和Rt△DEF）按图1所示的方式摆放，其中∠ACB=90°，CA=CB，∠FDE=90°，O是AB的中点，点D与点O重合，DF⊥AC于点M，DE⊥BC于点N，试判断线段OM与ON的数量关系，并说明理由．‎ 探究展示：小宇同学展示出如下正确的解法：‎ 解：OM=ON，证明如下：‎ 连接CO，则CO是AB边上中线，‎ ‎∵CA=CB，∴CO是∠ACB的角平分线．（依据1）‎ ‎∵OM⊥AC，ON⊥BC，∴OM=ON．（依据2）‎ 反思交流：‎ ‎（1）上述证明过程中的“依据1”和“依据2”分别是指：‎ 依据1： ‎ 依据2： ‎ ‎（2）你有与小宇不同的思考方法吗？请写出你的证明过程．‎ 拓展延伸：‎ ‎（3）将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置，使点D落在BA的延长线上，FD的延长线与CA的延长线垂直相交于点M，BC的延长线与DE垂直相交于点N，连接OM、ON，试判断线段OM、ON的数量关系与位置关系，并写出证明过程．‎ ‎【答案】（1）解：等腰三角形三线合一（或等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合）；角平分线上的点到角的两边距离相等。‎ ‎（2）证明：∵CA=CB，∴∠A=∠B。‎ ‎∵O是AB的中点，∴OA=OB。‎ ‎∵DF⊥AC，DE⊥BC，∴∠AMO=∠BNO=90°。‎ ‎∵在△OMA和△ONB中，∠A=∠B，OA=OB，∠AMO=∠BNO，‎ ‎∴△OMA≌△ONB（AAS）。∴OM=ON。‎ ‎（3）解：OM=ON，OM⊥ON。理由如下：‎ 连接CO，则CO是AB边上的中线。‎ ‎∵∠ACB=90°，∴OC=AB=OB。‎ 又∵CA=CB，‎ ‎∴∠CAB=∠B=45，∠1=∠2=45°，∠AOC=∠BOC=90°。∴∠2=∠B。‎ ‎∵BN⊥DE，∴∠BND=90°。‎ 又∵∠B=45°，∴∠3=45°。∴∠3=∠B。∴DN=NB。‎ ‎∵∠ACB=90°，∴∠NCM=90°。‎ 又∵BN⊥DE，∴∠DNC=90°。∴四边形DMCN是矩形。∴DN=MC。∴MC=NB。‎ ‎∴△MOC≌△NOB（SAS）。∴OM=ON，∠MOC=∠NOB。‎ ‎∴∠MOC﹣∠CON=∠NOB﹣∠CON，即∠MON=∠BOC=90°。‎ ‎∴OM⊥ON。‎ ‎【考点】等腰三角形的性质，角平分线的性质，全等三角形的判定和性质，矩形的判定和性质。‎ ‎【分析】（1）根据等腰三角形和角平分线的性质直接作答。‎ ‎（2）利用AAS证明△OMA≌△ONB即可。‎ ‎（3）利用SAS证明△MOC≌△NOB即可得到OM=ON，∠MOC=∠NOB。通过角的等量代换即可得∠MON=∠BOC=90°，而得到OM⊥ON。‎ ‎3. （2012福建厦门10分）已知ABCD，对角线AC与BD相交于点O，点P在边AD上，过点P分 别作PE⊥AC、PF⊥BD，垂足分别为E、F，PE＝PF．‎ ‎（1）如图，若PE＝，EO＝1，求∠EPF的度数；‎ ‎（2）若点P是AD的中点，点F是DO的中点，BF ＝BC＋3－4，求BC的长．‎ ‎【答案】解：（1）连接PO , ‎ ‎∵ PE＝PF，PO＝PO，PE⊥AC、PF⊥BD，‎ ‎∴ Rt△PEO≌Rt△PFO（HL）。‎ ‎∴∠EPO＝∠FPO。‎ 在Rt△PEO中， tan∠EPO＝＝，‎ ‎∴ ∠EPO＝30°。∴ ∠EPF＝60°。‎ ‎（2）∵点P是AD的中点，∴ AP＝DP。‎ 又∵ PE＝PF，∴ Rt△PEA≌Rt△PFD（HL）。‎ ‎∴∠OAD＝∠ODA。∴ OA＝OD。‎ ‎∴ AC＝2OA＝2OD＝BD。∴ABCD是矩形。 ‎ ‎∵ 点P是AD的中点，点F是DO的中点，∴ AO∥PF。‎ ‎∵ PF⊥BD，∴ AC⊥BD。∴ABCD是菱形。∴ABCD是正方形。‎ ‎∴ BD＝BC。‎ ‎∵ BF＝BD，∴BC＋3－4＝BC，解得，BC＝4。‎ ‎【考点】平行四边形的性质，角平分线的性质，三角形中位线定理，全等三角形的判定和性质，正方形的判定和性质，锐角三角函数定义。‎ ‎【分析】（1）连接PO，利用解直角三角形求出∠EPO=30°，再利用“HL”证明△PEO和△PFO全等，根据全等三角形对应角相等可得∠FPO=∠EPO，从而得解。‎ ‎（2）根据条件证出 ABCD是正方形。根据正方形的对角线与边长的关系列式计算即可得解。‎ ‎4. （2012甘肃白银10分）如图，点A，B，C，D在⊙O上，AB=AC，AD与BC相交于点E，，延长DB到点F，使，连接AF．‎ ‎（1）证明：△BDE∽△FDA；‎ ‎（2）试判断直线AF与⊙O的位置关系，并给出证明．‎ ‎【答案】解:（1）证明：在△BDE和△FDA中，∵FB＝BD，AE＝ED，∴。‎ 又∵∠BDE＝∠FDA，∴△BDE∽△FDA。‎ ‎（2）直线AF与⊙O相切。证明如下：‎ 连接OA，OB，OC，‎ ‎∵AB＝AC，BO＝CO，OA＝OA，‎ ‎∴△OAB≌△OAC（SSS）。∴∠OAB＝∠OAC。‎ ‎∴AO是等腰三角形ABC顶角∠BAC的平分线。‎ ‎∴AO⊥BC。‎ ‎∵△BDE∽FDA，得∠EBD＝∠AFD，∴BE∥FA。‎ ‎∵AO⊥BE，∴AO⊥FA。∴直线AF与⊙O相切。‎ ‎【考点】相似三角形的判定和性质，全等三角形的判定和性质，等腰三角形的性质，平行的判定和性质，切线的判定。‎ ‎【分析】（1）因为∠BDE公共，夹此角的两边BD：DF=ED：AD=2：3，由相似三角形的判定，可知△BDE∽△FDA。‎ ‎（2）连接OA、OB、OC，证明△OAB≌OAC，得出AO⊥BC．再由△BDE∽FDA，得出∠EBD=∠AFD，则BE∥FA，从而AO⊥FA，得出直线AF与⊙O相切。‎ ‎5. （2012广东广州14分）如图，在平行四边形ABCD中，AB=5，BC=10，F为AD的中点，CE⊥AB于E，设∠ABC=α（60°≤α＜90°）．‎ ‎（1）当α=60°时，求CE的长；‎ ‎（2）当60°＜α＜90°时，‎ ‎①是否存在正整数k，使得∠EFD=k∠AEF？若存在，求出k的值；若不存在，请说明理由．‎ ‎②连接CF，当CE2﹣CF2取最大值时，求tan∠DCF的值．‎ ‎【答案】解：（1）∵α=60°，BC=10，∴sinα=，即sin60°=，解得CE=。‎ ‎（2）①存在k=3，使得∠EFD=k∠AEF。理由如下：‎ 连接CF并延长交BA的延长线于点G，‎ ‎∵F为AD的中点，∴AF=FD。‎ 在平行四边形ABCD中，AB∥CD，∴∠G=∠DCF。‎ 在△AFG和△CFD中，‎ ‎∵∠G=∠DCF， ∠G=∠DCF，AF=FD，‎ ‎∴△AFG≌△CFD（AAS）。∴CF=GF，AG=CD。‎ ‎∵CE⊥AB，∴EF=GF。∴∠AEF=∠G。‎ ‎∵AB=5，BC=10，点F是AD的中点，∴AG=5，AF=AD=BC=5。∴AG=AF。‎ ‎∴∠AFG=∠G。‎ 在△AFG中，∠EFC=∠AEF+∠G=2∠AEF，‎ 又∵∠CFD=∠AFG，∴∠CFD=∠AEF。‎ ‎∴∠EFD=∠EFC+∠CFD=2∠AEF+∠AEF=3∠AEF，‎ 因此，存在正整数k=3，使得∠EFD=3∠AEF。‎ ‎②设BE=x，∵AG=CD=AB=5，∴EG=AE+AG=5﹣x+5=10﹣x，‎ 在Rt△BCE中，CE2=BC2﹣BE2=100﹣x2。‎ 在Rt△CEG中，CG2=EG2+CE2=（10﹣x）2+100﹣x2=200﹣20x。‎ ‎∵CF=GF（①中已证），∴CF2=（CG）2=CG2=（200﹣20x）=50﹣5x。‎ ‎∴CE2﹣CF2=100﹣x2﹣50+5x=﹣x2+5x+50=﹣（x﹣）2+50+。‎ ‎∴当x=，即点E是AB的中点时，CE2﹣CF2取最大值。‎ 此时，EG=10﹣x=10﹣，CE=，‎ ‎∴。‎ ‎【考点】锐角三角函数定义，特殊角的三角函数值，平行四边形的性质，对顶角的性质，全等三角形的判定和性质，直角三角形斜边上的中线性质，等腰三角形的性质，二次函数的最值，勾股定理。‎ ‎【分析】（1）利用60°角的正弦值列式计算即可得解。‎ ‎（2）①连接CF并延长交BA的延长线于点G，利用“角边角”证明△AFG和△CFD全等，根据全等三角形对应边相等可得CF=GF，AG=CD，再利用直角三角形斜边上的中线等于斜边的一半可得EF=GF，再根据AB、BC的长度可得AG=AF，然后利用等边对等角的性质可得∠AEF=∠G=∠AFG，根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EFC=2∠G，然后推出∠EFD=3∠AEF，从而得解。‎ ‎②设BE=x，在Rt△BCE中，利用勾股定理表示出CE2，表示出EG的长度，在Rt△CEG中，利用勾股定理表示出CG2，从而得到CF2，然后相减并整理，再根据二次函数的最值问题解答。‎ ‎6. （2012广东肇庆10分）如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC于点E，交BC于点D，连结BE、AD交于点P. 求证：‎ ‎（1）D是BC的中点；‎ ‎（2）△BEC ∽△ADC；‎ ‎（3）AB× CE=2DP×AD．‎ ‎【答案】证明：（1）∵AB是⊙O的直径，∴∠ADB=90°，即AD⊥BC。‎ ‎∵AB=AC，∴D是BC的中点。 （2）∵AB是⊙O的直径，∴∠AEB=∠ADB=90°，即∠CEB=∠CDA=90°，‎ ‎∵∠C是公共角，∴△BEC∽△ADC。‎ ‎（3）∵△BEC∽△ADC，∴∠CBE=∠CAD。‎ ‎∵AB=AC，AD=CD，∴∠BAD=∠CAD。∴∠BAD=∠CBE。‎ ‎∵∠ADB=∠BEC=90°，∴△ABD∽△BCE。‎ ‎∴。∴。‎ ‎∵BC=2BD，∴，即。‎ ‎∵∠BDP=∠BEC=90°，∠PBD=∠CBE，∴△BPD∽△BCE。∴。‎ ‎∴，即AB•CE=2DP•AD。‎ ‎【考点】圆周角定理，等腰三角形的性质，相似三角形的判定和性质。‎ ‎【分析】（1）由AB是⊙O的直径，可得AD⊥BC，又由AB=AC，由三线合一，即可证得D是BC的中点。‎ ‎（2）由AB是⊙O的直径，∠AEB=∠ADB=90°，又由∠C是公共角，即可证得△BEC∽△ADC。‎ ‎（3）易证得△ABD∽△BCE与△BPD∽△BCE，根据相似三角形的对应边成比例与BC=2BD，即可证得AB•CE=2DP•AD。‎ ‎7. （2012贵州毕节14分）如图，AB是⊙O的直径，AC为弦，D是的中点，过点D作EF⊥AC的延长线于E，交AB的延长线于E，交AB的延长线于F。‎ ‎（1）求证：EF是⊙O的切线；‎ ‎（2）若∠F=，AE=4，求⊙O的半径和AC的长。‎ ‎【答案】（1）证明：连接OD，‎ ‎∵D是的中点，∴∠BOD=∠A。‎ ‎∴OD∥AC。‎ ‎∵EF⊥AC，∴∠E=90°。∴∠ODF=90°。‎ ‎∴EF是⊙O的切线；‎ ‎（2）解：在△AEF中，∵∠E=90°，sin∠F= ，AE=4，‎ ‎∴。‎ 设⊙O的半径为R，则OD=OA=OB=R，AB=2R．‎ 在△ODF中，∵∠ODF=90°，sin∠F=，∴OF=3OD=3R。‎ ‎∵OF+OA=AF，∴3R+R=12，∴R=3。‎ 连接BC，则∠ACB=90°。‎ ‎∵∠E=90°，∴BC∥EF。∴AC：AE=AB：AF。‎ ‎∴AC：4=2R：4R，∴AC=2。‎ ‎∴⊙O的半径为3，AC的长为2。‎ ‎【考点】弧、圆周角和圆心角的关系，圆周角定理，平行的判定和性质，切线的判定，锐角三角函数定义，平行线分线段成比例定理。‎ ‎【分析】（1）连接OD，根据圆周角定理，可得∠BOD=∠A，则OD∥AC，从而得出∠ODF=90°，即EF是⊙O的切线。‎ ‎（2）先解直角△AEF，由sin∠F= ，得出AF=3AE=12，再在Rt△ODF中，由sin∠F=，得出OF=3OD，设⊙O的半径为R，由AF=12列出关于R的方程，解方程即可求出⊙O的半径。连接BC，证明BC∥EF，根据平行线分线段成比例定理得出AC：AE=AB：AF，即可求出AC的长。‎ ‎8. （2012江苏泰州12分）如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5，OA与⊙O相交于点 P，AB与⊙O相切于点B，BP的延长线交直线l于点C．‎ ‎（1）试判断线段AB与AC的数量关系，并说明理由；‎ ‎（2）若PC=，求⊙O的半径和线段PB的长；‎ ‎（3）若在⊙O上存在点Q，使△QAC是以AC为底边的等腰三角形，求⊙O的半径r的取值范围．‎ ‎【答案】解：（1）AB=AC。理由如下：‎ 连接OB。‎ ‎∵AB切⊙O于B，OA⊥AC，∴∠OBA=∠OAC=90°。‎ ‎∴∠OBP+∠ABP=90°，∠ACP+∠CPB=90°。‎ ‎∵OP=OB，∴∠OBP=∠OPB。‎ ‎∵∠OPB=∠APC，∴∠ACP=∠ABC。‎ ‎∴AB=AC。‎ ‎（2）延长AP交⊙O于D，连接BD，‎ 设圆半径为r，则由OA=5得，OP=OB=r，PA=5－r。‎ 又∵PC=，‎ ‎∴ 。‎ 由（1）AB=AC得，解得：r=3。‎ ‎∴AB=AC=4。‎ ‎∵PD是直径，∴∠PBD=90°=∠PAC。‎ ‎∵∠DPB=∠CPA，∴△DPB∽△CPA。∴，即，解得。‎ ‎ （3）作线段AC的垂直平分线MN，作OE⊥MN，‎ 则OE=AC=AB=。‎ 又∵圆O要与直线MN交点，∴OE=≤r，‎ ‎∴r≥。‎ 又∵圆O与直线l相离，∴r＜5。‎ ‎∴⊙O的半径r的取值范围为≤r＜5．‎ ‎【考点】切线的性质，三角形内角和定理，等腰三角形的判定和性质，勾股定理，直线与圆的位置关系，相似三角形的判定和性质。‎ ‎【分析】（1）连接OB，根据切线的性质和垂直得出∠OBA=∠OAC=90°，推出∠OBP+∠ABP=90°，‎ ‎∠ACP+∠CPB=90°，求出∠ACP=∠ABC，根据等腰三角形的判定推出即可。‎ ‎（2）延长AP交⊙O于D，连接BD，设圆半径为r，则OP=OB=r，PA=5－r，根据AB=AC推出 ‎，求出r，证△DPB∽△CPA，得出 ，代入求出PB即可。‎ ‎（3）根据已知得出Q在AC的垂直平分线上，作出线段AC的垂直平分线MN，作OE⊥MN，求出OE＜r，求出r范围，再根据相离得出r＜5，即可得出答案。‎ ‎9. （2012江苏南京10分）如图，A、B为⊙O上的两个定点，P是⊙O上的动点（P不与A、B重合），我们称∠APB为⊙O上关于A、B的滑动角。‎ ‎（1）已知∠APB是上关于点A、B的滑动角。‎ ‎① 若AB为⊙O的直径，则∠APB= ‎ ‎② 若⊙O半径为1，AB=，求∠APB的度数 ‎（2）已知为外一点，以为圆心作一个圆与相交于A、B两点，∠APB为上关于点A、B的滑动角，直线PA、PB分别交于点M、N（点M与点A、点N与点B均不重合），连接AN，试探索∠APB与∠MAN、∠ANB之间的数量关系。‎ ‎【答案】解：（1）①900。‎ ‎②如图，连接AB、OA、OB．‎ 在△AOB中，∵OA=OB=1．AB=，∴OA2+OB2=AB2。‎ ‎∴∠AOB=90°。‎ 当点P在优弧 AB 上时（如图1），∠APB=∠AOB=45°；‎ 当点P在劣弧 AB 上时（如图2），‎ ‎∠APB=（360°－∠AOB）=135°。‎ ‎（2）根据点P在⊙O1上的位置分为以下四种情况．‎ 第一种情况：点P在⊙O2外，且点A在点P与点M之间，点B在点P与点N之间，如图3，‎ ‎∵∠MAN=∠APB+∠ANB，‎ ‎∴∠APB=∠MAN-∠ANB。‎ 第二种情况：点P在⊙O2外，且点A在点P与点M之间，点N在点P与点B之间，如图4，‎ ‎∵∠MAN=∠APB+∠ANP=∠APB+（180°－∠ANB），‎ ‎∴∠APB=∠MAN+∠ANB－180°。‎ 第三种情况：点P在⊙O2外，且点M在点P与点A之间，点B在点P与点N之间，如图5，‎ ‎∵∠APB+∠ANB+∠MAN=180°，‎ ‎∴∠APB=180°－∠MAN－∠ANB。‎ 第四种情况：点P在⊙O2内，如图6，‎ ‎∠APB=∠MAN+∠ANB。‎ ‎【考点】圆周角定理，勾股定理逆定理，三角形内角和定理和外角性质。‎ ‎【分析】（1）①根据直径所对的圆周角等于90°即可得∠APB=900。‎ ‎②根据勾股定理的逆定理可得∠AOB=90°，再分点P在优弧上；点P在劣弧上两种情况讨论即可。‎ ‎（2）根据点P在⊙O1上的位置分为四种情况得到∠APB与∠MAN、∠ANB之间的数量关系。‎ ‎10. （2012四川宜宾10分）如图，⊙O1、⊙O2相交于P、Q两点，其中⊙O1的半径r1=2，⊙O2的半径r2=．过点Q作CD⊥PQ，分别交⊙O1和⊙O2‎ 于点C．D，连接CP、DP，过点Q任作一直线AB交⊙O1和⊙O2于点A．B，连接AP、BP、AC．DB，且AC与DB的延长线交于点E．‎ ‎（1）求证：；‎ ‎（2）若PQ=2，试求∠E度数．‎ ‎【答案】（1）证明：∵⊙O1的半径r1=2，⊙O2的半径r2=，∴PC=4，PD=2。‎ ‎∵CD⊥PQ，∴∠PQC=∠PQD=90°。‎ ‎∴PC．PD分别是⊙O1、⊙O2的直径，在⊙O1中，∠PAB=∠PCD，在⊙O2中，∠PBA=∠PDC，‎ ‎∴△PAB∽△PCD。∴，即。‎ ‎（2）解：在Rt△PCQ中，∵PC=2r1=4，PQ=2，∴cos∠CPQ=。∴∠CPQ=60°。‎ ‎∵在Rt△PDQ中，PD=2r2=2，PQ=2，∴sin∠PDQ=。∴∠PDQ=45°。‎ ‎∴∠CAQ=∠CPQ=60°，∠PBQ=∠PDQ=45°。‎ 又∵PD是⊙O2的直径，∴∠PBD=90°。∴∠ABE=90°﹣∠PBQ=45°。‎ 在△EAB中，∴∠E=180°﹣∠CAQ﹣∠ABE=75°。‎ 答：∠E的度数是75°。‎ ‎【考点】相交两圆的性质，相似三角形的判定和性质，锐角三角函数定义，特殊角的三角函数值，圆周角定理，三角形内角和定理。‎ ‎【分析】（1）求出PC、PD，证△PAB∽△PCD，得出，从而。‎ ‎（2）由cos∠CPQ=，求出∠CPQ=60°，同理求出∠PDQ=45°。由圆周角定理，得出 ‎∠CAQ=∠CPQ=60°，∠PBQ=∠PDQ=45°，求出∠PBD=90°，求出∠ABE=45°根据三角形的内角和定理求出即可。‎ ‎11. （2012四川广安9分）如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP．‎ ‎（1）求证：直线CP是⊙O的切线．‎ ‎（2）若BC=2，sin∠BCP=，求点B到AC的距离．‎ ‎（3）在第（2）的条件下，求△ACP的周长．‎ ‎【答案】解：（1）∵∠ABC=∠ACB且∠CAB=2∠BCP，在△ABC中，∠ABC+∠BAC+∠BCA=180°，‎ ‎∴2∠BCP+2∠BCA=180°。‎ ‎∴∠BCP+∠BCA=90°，即∠PCA=90°。‎ 又∵AC是⊙O的直径，∴直线CP是⊙O的切线。‎ ‎（2）如图，作BD⊥AC于点D，‎ ‎∵PC⊥AC，∴BD∥PC。∴∠PCB=∠DBC。‎ ‎∵C=2，sin∠BCP=‎ ‎∴，解得：DC=2。‎ ‎∴由勾股定理得：BD=4。∴点B到AC的距离为4。‎ ‎（3）如图，连接AN，‎ 在Rt△ACN中，，‎ 又CD=2，∴AD=AC﹣CD=5﹣2=3。‎ ‎∵BD∥CP，∴△ABD∽△ACP。‎ ‎∴，即。∴。‎ 在Rt△ACP中，。‎ ‎∴△ACP的周长为。‎ ‎【考点】切线的判定和性质，三角形内角和定理，等腰三角形的性质，勾股定理，相似三角形的判定和性质，锐角三角函数定义。‎ ‎【分析】（1））根据∠ABC=∠AC且∠CAB=2∠BCP，在△ABC中∠ABC+∠BAC+∠BCA=180°，得到2∠BCP+2∠BCA=180°，从而得到∠BCP+∠BCA=90°，证得直线CP是⊙O的切线。‎ ‎（2）作BD⊥AC于点D，得到BD∥PC，从而利用求得DC=2，再根据勾股定理求得点B到AC的距离为4。‎ ‎（3）先求出AC的长度，然后由BD∥PC求得△ABD∽△ACP，利用比例线段关系求得CP的长度，再由勾股定理求出AP的长度，从而求得△ACP的周长。‎ ‎12. （2012四川达州7分）如图，C是以AB为直径的⊙O上一点，过O作OE⊥AC于点E，过点A作 ‎⊙O的切线交OE的延长线于点F，连结CF并延长交BA的延长线于点P.‎ ‎（1）求证：PC是⊙O的切线.‎ ‎（2）若AF=1，OA=，求PC的长. ‎ ‎【答案】解：（1）证明：连结OC， ‎  ∵OE⊥AC，∴AE=CE。∴FA=FC。‎ ∴∠FAC=∠FCA。‎ ‎∵OA=OC，∴∠OAC=∠OCA。‎ ‎∴∠OAC+∠FAC=∠OCA+∠FCA，即∠FAO=∠FCO。‎ ‎∵FA与⊙O相切，且AB是⊙O的直径，∴FA⊥AB。∴∠FCO=∠FAO=90°。‎ 又∵OC是⊙O的半径，∴PC是⊙O的切线。‎ ‎（2）∵PC是⊙O的切线，∴∠PCO=90°。‎ 而∠FPA=∠OPC，∠PAF=90°，∴△PAF∽△PCO 。∴。‎ ‎∵CO=OA=，AF=1，∴PC=PA 。‎ 设PA=x，则PC=‎ 在Rt△PCO中，由勾股定理得， ，解得：。‎ ‎∴PC。‎ ‎【考点】切线的判定和性质，垂径定理，圆周角定理，相似三角形的判定和性质，勾股定理。‎ ‎【分析】（1）连接OC，根据垂径定理，利用等角代换可证明∠FAC=∠FCA，然后根据切线的性质得出∠FAO=90°，然后即可证明结论。‎ ‎ （2）先证明△PAF∽△PCO，利用相似三角形的性质得出PC与PA的关系，在Rt△PCO中，利用勾股定理可得出x的值，从而也可得出PC得长。‎ ‎13. （2012四川德阳14分） 如图，已知点C是以AB为直径的⊙O上一点，CH⊥AB于点H，过点B作⊙O 的切线交直线AC于点D，点E为CH的中点，连结并延交BD于点F，直线CF交AB的延长线于G.‎ ‎⑴求证：AE·FD=AF·EC；‎ ‎⑵求证：FC=FB；‎ ‎⑶若FB=FE=2，求⊙O 的半径r的长.‎ ‎【答案】（1）证明：∵BD是⊙O的切线，∴∠DBA=90°。‎ ‎∵CH⊥AB，∴CH∥BD。∴△AEC∽△AFD。‎ ‎∴。∴AE•FD=AF•EC。‎ ‎（2）证明：∵CH∥BD，∴△AEC∽△AFD，△AHE∽△ABF。∴。‎ ‎∵CE=EH（E为CH中点），∴BF=DF。‎ ‎∵AB为⊙O的直径，∴∠ACB=∠DCB=90°。∴CF=DF=BF，即CF=BF。‎ ‎（3）解：∵BF=CF=DF（已证），EF=BF=2，∴EF=FC。∴∠FCE=∠FEC。‎ ‎∵∠AHE=∠CHG=90°，∴∠FAH+∠AEH=90°，∠G+∠GCH=90°。‎ ‎∵∠AEH=∠CEF，∴∠G=∠FAG。∴AF=FG。‎ ‎∵FB⊥AG，∴AB=BG。‎ 连接OC，BC，‎ ‎∵BF切⊙O于B，∴∠FBC=∠CAB。‎ ‎∵OC=OA，CF=BF，‎ ‎∴∠FCB=∠FBC，∠OCA=∠OAC ‎∴∠FCB=∠CAB。‎ ‎∵∠ACB=90°，∴∠ACO+∠BCO=90°。∴∠FCB+∠BCO=90°，即OC⊥CG。‎ ‎∴CG是⊙O切线。‎ ‎∵GBA是⊙O割线，FB=FE=2，由切割线定理得：（2+FG）2=BG×AG=2BG2，‎ ‎【注，没学切割线定理的可由△AGC∽△CGB求得】‎ 在Rt△BFG中，由勾股定理得：BG2=FG2﹣BF2，∴FG2﹣4FG﹣12=0。‎ 解得：FG=6，FG=﹣2（舍去）。‎ 由勾股定理得：AB=BG=。‎ ‎∴⊙O的半径r是。‎ ‎【考点】切线的判定和性质，等腰三角形判定和的性质，直角三角形斜边上的中线性质，勾股定理，圆周角定理，切割线定理，相似三角形的判定和性质。‎ ‎【分析】（1）由BD是⊙O的切线得出∠DBA=90°，推出CH∥BD，证△AEC∽△AFD，得出比例式即可。‎ ‎（2）证△AEC∽△AFD，△AHE∽△ABF，推出BF=DF，根据直角三角形斜边上中线性质得出CF=DF=BF即可。‎ ‎（3）求出EF=FC，求出∠G=∠FAG，推出AF=FG，求出AB=BG，连接OC，BC，求出∠FCB=∠CAB推出CG是⊙O切线，由切割线定理（或△AGC∽△CGB）得出（2+FG）2=BG×AG=2BG2，在Rt△BFG中，由勾股定理得出BG2=FG2﹣BF2，推出FG2﹣4FG﹣12=0，求出FG即可，从而由勾股定理求得AB=BG 的长，从而得到⊙O的半径r。‎ ‎14. （2012四川资阳9分）如图，在△ABC中，AB＝AC，∠A＝30°，以AB为直径的⊙O交BＣ于点D，交AC于点，连结DE，过点B作BP平行于DE，交⊙O于点P，连结EP、CP、OP．‎ ‎（1）(3分)BD＝DC吗？说明理由；‎ ‎（2）(3分)求∠BOP的度数；‎ ‎（3）(3分)求证：CP是⊙O的切线；‎ 如果你解答这个问题有困难，可以参考如下信息：‎ 为了解答这个问题，小明和小强做了认真的探究，然后分别用不同的思路完成了这个题目．在进行小组交流的时候，小明说：“设OP交AC于点G，证△AOG∽△CPG”；小强说：“过点C作CH⊥AB于点H，证四边形CHOP是矩形”．‎ ‎【答案】解：（1）BD=DC。理由如下：连接AD，‎ ‎∵AB是直径，∴∠ADB=90°。‎ ‎∵AB=AC，∴BD=DC。‎ ‎（2）∵AD是等腰△ABC底边上的中线，‎ ‎ ∴∠BAD=∠CAD 。∴。‎ ‎∴BD=DE。‎ ‎∴BD=DE=DC。∴∠DEC=∠DCE。‎ ‎ ∵△ABC中，AB=AC，∠A=30°，‎ ‎∴∠DCE=∠ABC= (180°－30°)=75°。∴∠DEC=75°。‎ ‎∴∠EDC=180°－75°－75°=30°。‎ ‎∵BP∥DE，∴∠PBC=∠EDC=30°。‎ ‎∴∠ABP=∠ABC－∠PBC=75°－30°=45°。‎ ‎∵OB=OP，∴∠OBP=∠OPB=45°。∴∠BOP=90°。‎ ‎（3）设OP交AC于点G，则∠AOG=∠BOP =90°。‎ 在Rt△AOG中，∵∠OAG=30°，∴。‎ 又∵，∴。∴。‎ 又∵∠AGO=∠CGP，[w∴△AOG∽△CPG。‎ ‎∴∠GPC=∠AOG=90°。∴CP是⊙的切线。‎ ‎【考点】圆周角定理，等腰三角形的性质，三角形内角和定理，相似三角形的判定和性质，切线的判定。‎ ‎【分析】（1）连接AD，由圆周角定理可知∠ADB=90°，再由AB=AC可知△ABC是等腰三角形，故BD=DC。‎ ‎（2）由于AD是等腰三角形ABC底边上的中线，所以∠BAD=∠CAD，故，从而可得出BD=DE，故BD=DE=DC，所以∠DEC=∠DCE，△ABC中由等腰三角形的性质可得出∠ABC=75°，故∠DEC=75°由三角形内角和定理得出∠EDC的度数，再根据BP∥DE可知∠PBC=∠EDC=30°，进而得出∠ABP的度数，再由OB=OP，可知∠OBP=∠OPB，由三角形内角和定理即可得出∠BOP=90°。‎ ‎（3）设OP交AC于点G，由∠BOP=90°可知∠AOG=90°在Rt△AOG中，由∠OAG=30°，可知，由得， ，由∠AGO=∠CGP可得出△AOG∽△CPG，由相似三角形形的性质可知∠GPC=∠AOG=90°，故可得出CP是⊙O的切线。 ‎ ‎15. （2012山东滨州12分）如图1，l1，l2，l3，l4是一组平行线，相邻2条平行线间的距离都是1个单位长度，正方形ABCD的4个顶点A，B，C，D都在这些平行线上．过点A作AF⊥l3于点F，交l2于点H，过点C作CE⊥l2于点E，交l3于点G．‎ ‎（1）求证：△ADF≌△CBE；‎ ‎（2）求正方形ABCD的面积；‎ ‎（3）如图2，如果四条平行线不等距，相邻的两条平行线间的距离依次为h1，h2，h3，试用h1，h2，h3‎ 表示正方形ABCD的面积S．‎ ‎【答案】解：（1）证明：在Rt△AFD和Rt△CEB中，‎ ‎∵AD=BC，AF=CE，∴Rt△AFD≌Rt△CEB（HL）。‎ ‎（2）∵∠ABH+∠CBE=90°，∠ABH+∠BAH=90°，∴∠CBE=∠BAH。‎ 又∵AB=BC，∠AHB=∠CEB=90°，∴△ABH≌△BCE（AAS）。‎ 同理可得，△ABH≌△BCE≌△CDG≌△DAF。‎ ‎∴S正方形ABCD=4S△ABH+S正方形HEGF=4××2×1+1+1=5。‎ ‎（3）由（1）知，△AFD≌△CEB，故h1=h3，‎ 由（2）知，△ABH≌△BCE≌△CDG≌△DAF，‎ ‎∴S正方形ABCD=4S△ABH+S正方形HEGF=4×（h1+h2）•h1+h22=2h12+2h1h2+h22．‎ ‎【考点】全等三角形的判定和性质，平行线之间的距离，正方形的性质。‎ ‎【分析】（1）直接根据HL定理得出Rt△AFD≌Rt△CEB。‎ ‎（2）由AAS定理得出△ABH≌△BCE≌△CDG≌△DAF，再根据S正方形ABCD=4S△ABH+S正方形HEGF即可得出结论。‎ ‎（3）由△AFD≌△CEB可得出h1=h3，再根据（2）中△ABH≌△BCE≌△CDG≌△DAF，可知 S正方形ABCD=4S△ABH+S正方形HEGF，从而得出结论。‎ ‎16. （2012山东泰安10分）如图，E是矩形ABCD的边BC上一点，EF⊥AE，EF分别交AC，CD于点M，F，BG⊥AC，垂足为C，BG交AE于点H．‎ ‎（1）求证：△ABE∽△ECF；‎ ‎（2）找出与△ABH相似的三角形，并证明；‎ ‎（3）若E是BC中点，BC=2AB，AB=2，求EM的长．‎ ‎【答案】解：（1）证明：∵四边形ABCD是矩形，∴∠ABE=∠ECF=90°．‎ ‎∵AE⊥EF，∠AEB+∠FEC=90°，∴∠AEB+∠BEA=90°。‎ ‎∴∠BAE=∠CEF。∴△ABE∽△ECF。‎ ‎（2）△ABH∽△ECM。证明如下：‎ ‎∵BG⊥AC，∴∠ABG+∠BAG=90°。∴∠ABH=∠ECM。‎ 由（1）知，∠BAH=∠CEM，∴△ABH∽△ECM。‎ ‎（3）作MR⊥BC，垂足为R，‎ ‎∵AB=BE=EC=2，‎ ‎∴AB：BC=MR：RC=2，∠AEB=45°。‎ ‎∴∠MER=45°，CR=2MR。‎ ‎∴MR=ER=。∴EM=。‎ ‎【考点】矩形的性质，相似三角形的判定和性质，解直角三角形，锐角三角函数，特殊角的三角函数值。‎ ‎【分析】（1）由四边形ABCD是矩形，可得∠ABE=∠ECF=90°，又由EF⊥AE，利用同角的余角相等，可得∠BAE=∠CEF，然后利用有两组角对应相等的两个三角形相似，即可证得：△ABE∽△ECF。‎ ‎（2）由BG⊥AC，易证得∠ABH=∠ECM，又由（1）中∠BAH=∠CEM，即可证得 ‎△ABH∽△ECM。‎ ‎（3）首先作MR⊥BC，垂足为R，由AB：BC=MR：RC=2，∠AEB=45°，即可求得MR的长，又由EM= 即可求得答案。‎ ‎17. （2012山东聊城10分）如图，⊙O是△ABC的外接圆，AB=AC=10，BC=12，P是上的一个动点，过点P作BC的平行线交AB的延长线于点D．‎ ‎（1）当点P在什么位置时，DP是⊙O的切线？请说明理由；‎ ‎（2）当DP为⊙O的切线时，求线段DP的长．‎ ‎【答案】解：（1）当点P是的中点时，DP是⊙O的切线。理由如下：‎ 连接AP。‎ ‎∵AB=AC，∴。‎ 又∵，∴。∴PA是⊙O的直径。‎ ‎∵，∴∠1=∠2。‎ 又∵AB=AC，∴PA⊥BC。‎ 又∵DP∥BC，∴DP⊥PA。∴DP是⊙O的切线。‎ ‎（2）连接OB，设PA交BC于点E。．‎ 由垂径定理，得BE=BC=6。‎ 在Rt△ABE中，由勾股定理，得：AE=。‎ 设⊙O的半径为r，则OE=8﹣r，‎ 在Rt△OBE中，由勾股定理，得：r2=62+（8﹣r）2，解得r=。‎ ‎∵DP∥BC，∴∠ABE=∠D。‎ 又∵∠1=∠1，∴△ABE∽△ADP，‎ ‎∴，即，解得：。‎ ‎【考点】圆心角、弧、弦的关系，圆周角定理，切线的判定，勾股定理，垂径定理，相似三角形的判定和性质。‎ ‎【分析】（1）根据当点P是的中点时，得出，得出PA是⊙O的直径，再利用DP∥BC，得出DP⊥PA，问题得证。‎ ‎（2）利用切线的性质，由勾股定理得出半径长，进而得出△ABE∽△ADP，即可得出DP的长。‎ ‎18. （2012山东东营10分）‎ ‎（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．求证：CE＝CF；‎ ‎（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD．‎ ‎（3）运用（1）（2）解答中所积累的经验和知识，完成下题：‎ 如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE=10, 求直角梯形ABCD的面积．‎ ‎【答案】解：（1）证明：在正方形ABCD中，∵BC＝CD，∠B＝∠CDF，BE＝DF，‎ ‎∴△CBE≌△CDF（SAS）。∴CE＝CF。‎ ‎（2）证明： 如图，延长AD至F，使DF=BE．连接CF。‎ ‎ 由（1）知△CBE≌△CDF，‎ ‎∴∠BCE＝∠DCF。‎ ‎∴∠BCE＋∠ECD＝∠DCF＋∠ECD，‎ 即∠ECF＝∠BCD＝90°。‎ 又∠GCE＝45°，∴∠GCF＝∠GCE＝45°。‎ ‎∵CE＝CF，∠GCE＝∠GCF，GC＝GC，‎ ‎∴△ECG≌△FCG（SAS）。∴GE＝GF，‎ ‎∴GE＝DF＋GD＝BE＋GD。‎ ‎（3）如图，过C作CG⊥AD，交AD延长线于G．‎ 在直角梯形ABCD中，∵AD∥BC，∴∠A＝∠B＝90°。‎ 又∠CGA＝90°，AB＝BC，‎ ‎∴四边形ABCD 为正方形。 ∴AG＝BC。‎ 已知∠DCE＝45°，‎ 根据（1）（2）可知，ED＝BE＋DG。 ‎ ‎∴10=4+DG，即DG=6。‎ 设AB＝x，则AE＝x－4，AD＝x－6，‎ 在Rt△AED中，∵DE2=AD2＋AE2，即102=（x－6）2＋（x－4）2。‎ 解这个方程，得：x=12或x=－2（舍去）。‎ ‎∴AB=12。‎ ‎∴。‎ ‎∴梯形ABCD的面积为108。‎ ‎【考点】正方形的性质，全等三角形的判定和性质，勾股定理，直角梯形。‎ ‎【分析】（1）由四边形是ABCD正方形，易证得△CBE≌△CDF（SAS），即可得CE=CF。‎ ‎（2）延长AD至F，使DF=BE，连接CF，由（1）知△CBE≌△CDF，易证得∠ECF=∠BCD=90°，又由∠GCE=45°，可得∠GCF=∠GCE=45°，即可证得△ECG≌△FCG，从而可得GE=BE+GD。‎ ‎（3）过C作CG⊥AD，交AD延长线于G，易证得四边形ABCG为正方形，由（1）（2）可知，ED=BE+DG，即可求得DG的长，设AB=x，在Rt△AED中，由勾股定理DE2=AD2+AE2，可得方程，解方程即可求得AB的长，从而求得直角梯形ABCD的面积。‎ ‎19. （2012广西来宾10分）如图，AB是⊙O的直径，点C是⊙O上一点，∠BAC的平分线AD交⊙O于点D，过点D垂直于AC的直线交AC的延长线于点E．‎ ‎（1）求证：DE是⊙O的切线；‎ ‎（2）如图AD=5，AE=4，求⊙O的直径．‎ ‎【答案】（1）证明：如图，连接OD， ‎ ‎∵AD为∠CAB的平分线，∴∠CAD=∠BAD。‎ 又OA=OD，∴∠BAD=∠ODA。∴∠CAD=∠ODA。‎ ‎∴AC∥OD。∴∠E+∠EDO=180°。‎ 又AE⊥ED，即∠E=90°，∴∠EDO=90°。‎ ‎∴OD为圆O的切线。 ‎ ‎（2）解：如图，连接BD，‎ ‎∵AB为圆O的直径，∴∠ADB=90°。‎ 在Rt△AED中，AE=4，AD=5，∴。‎ 又∵∠EAD=∠DAB，在Rt△ABD中，∴。‎ ‎∴，即圆的直径为。‎ ‎【考点】等腰三角形的性质，平行的判定和性质，切线的判定，圆周角定理，锐角三角函数定义，特殊角的三角函数值。‎ ‎【分析】（1）连接OD，由AD为角平分线，得到一对角相等，再由OA=OD，得到一对角相等，等量代换得到一对内错角相等，根据内错角相等两直线平行可得AC∥OD，由两直线平行同旁内角互补，得到∠E与∠EDO互补，再由∠E为直角，可得∠EDO为直角，即DE为圆O的切线。‎ ‎（2）连接BD，由AB为⊙O的直径，根据直径所对的圆周角为直角的性质，得到∠ADB=90°。在Rt△AED中，由AE和AD的长，根据锐角三角函数定义求出cos∠EAD。又在Rt△ABD中，根据锐角三角函数定义得到 ，即可求出直径AB的长。‎ ‎20. （2012广西柳州10分）如图，AB是⊙O的直径，AC是弦．‎ ‎（1）请你按下面步骤画图（画图或作辅助线时先使用铅笔画出，确定后必须使用黑色字迹的签字笔描黑）；‎ 第一步，过点A作∠BAC的角平分线，交⊙O于点D；‎ 第二步，过点D作AC的垂线，交AC的延长线于点E．‎ 第三步，连接BD．‎ ‎（2）求证：AD2=AE•AB；‎ ‎（3）连接EO，交AD于点F，若‎5AC=3AB，求的值．‎ ‎【答案】解：（1）如图：‎ ‎（2）证明：∵AB是⊙O的直径，∴∠ADB=90°。‎ ‎ 又∵DE⊥AC，∴∠AED=90°。‎ ‎∵AD平分∠CAB，∴∠CAD=∠DAB。∴Rt△ADE∽Rt△ABD。‎ ‎∴AD：AB=AE：AD，∴AD2=AE•AB。‎ ‎（3）如图，连接OD、BC，它们交于点G， ‎ ‎∵‎5AC=3AB，即AC：AB=3：5，∴不妨设AC=3x，AB=5x，‎ ‎∵AB是⊙O的直径，∴∠ACB=90°。∴∠ECG=90°。‎ 又∵∠CAD=∠DAB，∴。∴OD垂直平分BC。‎ ‎∴OD∥AE，OG=AC=x。∴四边形ECGD为矩形。‎ ‎∴CE=DG=OD－OG=x－x =x。∴AE=AC+CE=3x+x=4x。‎ ‎∵AE∥OD，∴△AEF∽△DOF。∴AE：OD=EF：OF，∴EF：OF=4x：x=8：5。‎ ‎∴。‎ ‎【考点】圆的综合题，圆周角定理，相似三角形的判定和性质，垂径定理，矩形的判定和性质。‎ ‎【分析】（1）根据基本作图作出∠BAC的角平分线AD交⊙O于点D；点D作AC的垂线，垂足为点E。‎ ‎（2）根据直径所对的圆周角为直角得到∠ADB=90°，DE⊥AC，则∠AED=90°，又由AD平分∠CAB 得到∠CAD=∠DAB，根据相似三角形的判定得到Rt△ADE∽Rt△ABD，根据相似的性质得到AD：AB=AE：AD，利用比例的性质即可得到AD2=AE•AB。‎ ‎（3）连接OD、BC，它们交于点G，由‎5AC=3AB，则不妨设AC=3x，AB=5x，根据直径所对 的圆周角为直角得到∠ACB=90°，由∠CAD=∠DAB得到，根据垂径定理的推论得到OD垂直平分BC，则有OD∥AE，OG=AC=x，并且得到四边形ECGD为矩形，则可求出CE，从而计算出AE，利用AE∥OD可得到△AEF∽△DOF，则AE：OD=EF：OF，即EF：OF=4x：x=8：5，然后根据比例的性质即可得到 的值。‎ ‎21. （2012广西桂林10分）如图，等圆⊙O1和⊙O2相交于A、B两点，⊙O1经过⊙O2的圆心，顺次连接 A、O1、B、O2．‎ ‎(1)求证：四边形AO1BO2是菱形；‎ ‎(2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E，连接CO2交AE于D，求证：CE＝2O2D；‎ ‎(3)在(2)的条件下，若△AO2D的面积为1，求△BO2D的面积．‎ ‎【答案】解：（1）证明：∵⊙O1与⊙O2是等圆，∴AO1=O1B=BO2=O‎2A。‎ ‎∴四边形AO1BO2是菱形。‎ ‎（2）证明：∵四边形AO1BO2是菱形，∴∠O1AB=∠O2AB。‎ ‎∵CE是⊙O1的切线，AC是⊙O1的直径，∴∠ACE=∠AO‎2C=90°。‎ ‎∴△ACE∽△AO2D。∴，即CE=2DO2。‎ ‎（3）∵四边形AO1BO2是菱形，∴AC∥BO2。∴△ACD∽△BO2D。‎ ‎∴。∴AD=2BD。‎ ‎∵S，∴。‎ ‎【考点】相交两圆的性质，菱形的判定和性质，圆周角定理，相似三角形的判定和性质。‎ ‎【分析】（1）根据⊙O1与⊙O2是等圆，可得AO1=O1B=BO2=O‎2A，利用四条边都相等的四边形是菱形可判定出结论。‎ ‎（2）根据已知得出△ACE∽△AO2D，从而得出，即可得出结论。‎ ‎（3）首先证明△ACD∽△BO2D，得出 ，AD=2BD，再利用等高不等底的三角形面积关系得出答案即可。‎ ‎22. （2012广西北海10分）如图，AB是O的直径，AE交O于点E，且与O的切线CD互相垂直，垂足 为D。‎ ‎（1）求证：∠EAC＝∠CAB；‎ ‎（2）若CD＝4，AD＝8：‎ ‎①求O的半径；‎ ‎②求tan∠BAE的值。‎ ‎【答案】（1）证明：连接OC。 ‎ ‎∵CD是⊙O的切线，∴CD⊥OC。‎ 又∵CD⊥AE，∴OC∥AE。∴∠1＝∠3。‎ ‎∵OC＝OA，∴∠2＝∠3。‎ ‎∴∠1＝∠2，即∠EAC＝∠CAB。‎ ‎（2）解：①连接BC。‎ ‎∵AB是⊙O的直径，CD⊥AE于点D，‎ ‎∴∠ACB＝∠ADC＝90°。‎ ‎∵∠1＝∠2，∴△ACD∽△ABC。∴。‎ ‎∵AC2＝AD2＋CD2＝42＋82＝80，‎ ‎∴AB＝＝10。‎ ‎∴⊙O的半径为10÷2＝5。‎ ‎②连接CF与BF。‎ ‎∵四边形ABCF是⊙O的内接四边形，‎ ‎∴∠ABC＋∠AFC＝180°。‎ ‎∵∠DFC＋∠AFC＝180°，∴∠DFC＝∠ABC。‎ ‎∵∠2＋∠ABC＝90°， ∠DFC＋∠DCF＝90°，‎ ‎∴∠2＝∠DCF。‎ ‎∵∠1＝∠2，∴∠1＝∠DCF。‎ ‎∵∠CDF＝∠CDF，∴△DCF∽△DAC。∴ 。∴DF＝＝2。‎ ‎∴AF＝AD－DF＝8－2＝6。‎ ‎∵AB是⊙O的直径，∴∠BFA＝90°。‎ ‎∴BF＝＝8。∴tan∠BAD＝。 ‎ ‎【考点】切线的性质，平行的判定和性质，等腰三角形的性质，圆周角定理，勾股定理，相似三角形的判定和性质，锐角三角函数定义。‎ ‎【分析】（1）连接OC，由CD是⊙O的切线，CD⊥OC，又由CD⊥AE，即可判定OC∥AE，根据平行线的性质与等腰三角形的性质，即可证得∠EAC=∠CAB。‎ ‎（2）①连接BC，易证得△ACD∽△ABC，根据相似三角形的对应边成比例，即可求得AB的长，‎ 从而可得⊙O的半径长。‎ ‎ ②连接CF与BF．由四边形ABCF是⊙O的内接四边形，易证得△DCF∽△DAC，然后根据 相似三角形的对应边成比例，求得AF的长，又由AB是⊙O的直径，即可得∠BFA是直角，利用勾股定理求得BF的长，即可求得tan∠BAE的值。‎ ‎23. （2012内蒙古呼和浩特8分）如图，已知AB为⊙O的直径，PA与⊙O相切于点A，线段OP与弦AC垂直并相交于点D，OP与弧AC相交于点E，连接BC．‎ ‎（1）求证：∠PAC=∠B，且PA•BC=AB•CD；‎ ‎（2）若PA=10，sinP=，求PE的长．‎ ‎【答案】（1）证明：∵PA是⊙O的切线，AB是直径，∴∠PAO=90°，∠C=90°。‎ ‎∴∠PAC+∠BAC=90°，∠B+∠BAC=90°。∴∠PAC=∠B。‎ 又∵OP⊥AC，∴∠ADP=∠C=90°。∴△PAD∽△ABC，∴AP：AB=AD：BC，‎ ‎∵在⊙O中，AD⊥OD，∴AD=CD。∴AP：AB=CD：BC。∴PA•BC=AB•CD；‎ ‎（2）解：∵sinP=，且AP=10，∴。∴AD=6。∴AC=2AD=12。‎ 在Rt△ADP中，根据勾股定理得：。‎ 又∵△PAD∽△ABC，∴AP：AB=PD：AC。∴AB==15。∴AO=。‎ 在Rt△APO中，根据勾股定理得：。‎ ‎∴PE=OP﹣OE= ﹣=5。‎ ‎【考点】切线的性质，勾股定理，圆周角定理，垂径定理，相似三角形的判定和性质，锐角三角函数定义。‎ ‎【分析】（1）由PA为圆O的切线，利用切线的性质得到AP垂直于AB，可得出∠PAO为直角，得到∠PAD与∠DAO互余，再由AB为圆O的直径，根据直径所对的圆周角为直角，可得出∠ACB为直角，得到∠DAO与∠B互余，根据同角的余角相等可得出∠PAC=∠B，再由一对直角相等，利用两对对应角相等的两三角形相似可得出△APD与△ABC相似，由相似得比例，再由OD垂直于AC，利用垂径定理得到AD=CD，等量代换可得证。‎ ‎（2）在Rt△APD中，由PA及sinP的值求出AD的长，再利用勾股定理求出PD的长，从而确定出AC的长，由（1）两三角形相似得到的比例式，将各自的值代入求出AB的上，求出半径AO的长，在Rt△APO中，由AP及AO的长，利用勾股定理求出OP的长，用OP﹣OE即可求出PE的长。‎