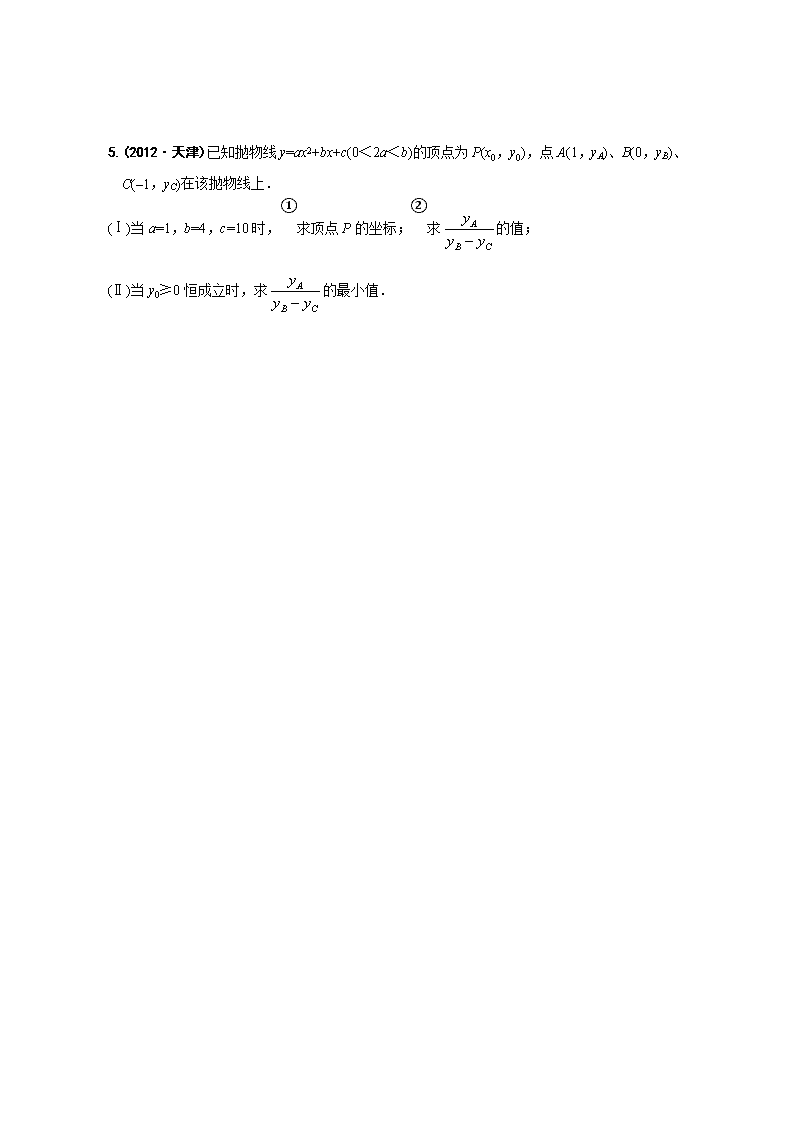20010年—2016年天津中考数学压轴题学生版 21页

20010 年—2016 年天津中考压轴题解析 3.(2010·天津)在平面直角坐标系中，已知抛物线 与 轴交于点 、 (点 在点 的左侧)，与 轴的正半轴交于点 ，顶点为 . (Ⅰ)若 ， ，求此时抛物线顶点 的坐标； (Ⅱ)将(Ⅰ )中 的 抛 物 线 向 下 平 移 ，若 平 移 后 ，在 四 边 形 ABEC 中 满 足 S △BCE = S△ABC，求此 时直线 的解析式； (Ⅲ)将(Ⅰ)中的抛物线作适当的平移，若平移后，在四边形 ABEC 中满足 S△BCE = 2S△AOC，且顶点 恰好落在直线 上，求此时抛物线的解析式. 2y x bx c= − + + x A B A B y C E 2b = 3c = E BC E 4 3y x= − + 4.(2011·天津)已知抛物线 ： ．点 F(1，1)． (Ⅰ) 求抛物线 的顶点坐标； (Ⅱ) ①若抛物线 与 y 轴的交点为 A．连接 AF，并延长交抛物线 于点 B，求证： ②抛物线 上任意一点 P( ))( )．连接 PF．并延长交抛物线 于点 Q( )， 试判断 是否成立？请说明理由； (Ⅲ) 将抛物线 作适当的平移．得抛物线 ： ，若 时． 恒成立， 求 m 的最大值． 1C 2 1 1 12y x x= − + 1C 1C 1C 1 1 2AF BF + = 1C P Px y， 0 1Px< < 1C Q Qx y， 1 1 2PF QF + = 1C 2C 2 2 1 ( )2y x h= − 2 x m< ≤ 2y x≤ 5.(2012·天津)已知抛物线 y=ax2+bx+c(0＜2a＜b)的顶点为 P(x0，y0)，点 A(1，yA)、B(0，yB)、 C(–1，yC)在该抛物线上． (Ⅰ)当 a=1，b=4，c=10 时，①求顶点 P 的坐标；②求 的值； (Ⅱ)当 y0≥0 恒成立时，求 的最小值． A B C y y y− A B C y y y− 6.(2013·天津)已知抛物线 y1=ax2+bx+c(a≠0)的对称轴是直线 l，顶点为点 M．若自变量 x 和函数值 y1 的部分对应值如下表所示： (Ⅰ)求 y1 与 x 之间的函数关系式； (Ⅱ)若经过点 T(0，t)作垂直于 y 轴的直线 l′，A 为直线 l′上的动点，线段 AM 的垂直平分线交直线 l 于点 B，点 B 关于直线 AM 的对称点为 P，记 P(x，y2)． (1)求 y2 与 x 之间的函数关系式； (2)当 x 取任意实数时，若对于同一个 x，有 y1＜y2 恒成立，求 t 的取值范围． x … –1 0 3 … y1=ax2+bx+c … 0 0 …9 4 A F M E O P x y 1 7.(2014·天津) 在平面直角坐标系中，O 为原点，直线 l：x=1，点 A(2，0)，点 E、点 F、点 M 都在直线 l 上，且点 E 和点 F 关于点 M 对称，直线 EA 与直线 OF 交于点 P. (Ⅰ)若点 M 的坐标为(1，–1). ① 当点 F 的坐标为(1，1)时，如图，求点 P 的坐标； ② 当点 F 为直线 l 上的动点时，记点 P(x，y)，求 y 关于 x 的函数解析式； (Ⅱ)若点 M (1，m)，点 F(1，t)，其中 t ≠0.过点 P 作 PQ⊥l 于点 Q，当 OQ＝PQ 时，试用含 t 的式子表示 m. 8.(2015·天津)已知二次函数 y=x2+bx+c(b，c 为常数)． (Ⅰ)当 b=2，c= –3 时，求二次函数的最小值； (Ⅱ)当 c=5 时，若在函数值 y=l 的情况下，只有一个自变量 x 的值与其对应，求此时二次函数的解析 式； (Ⅲ)当 c=b2 时，若在自变量 x 的值满足 b≤x≤b+3 的情况下，与其对应的函数值 y 的最小值为 21， 求此时二次函数的解析式． 9.（2016 年）已知抛物线 C： 的顶点为 P，与 y 轴的交点为 Q，点 F（1， ）. （Ⅰ）求点 P，Q 的坐标； （Ⅱ）将抛物线 C 向上平移得到抛物线 C′，点 Q 平移后的对应点为 Q′，且 FQ′＝OQ′. ① 求抛物线 C′的解析式； ② 若点 P 关于直线 Q′F 的对称点为 K，射线 FK 与抛物线 C′相交于点 A，求点 A 的坐标. 2 2 1y x x= − + 1 2 E y xFBDA O C 1x = 解析版 3.(2010·天津)在平面直角坐标系中，已知抛物线 与 轴交于点 、 (点 在点 的左侧)，与 轴的正半轴交于点 ，顶点为 . (Ⅰ)若 ， ，求此时抛物线顶点 的坐标； (Ⅱ)将(Ⅰ )中 的 抛 物 线 向 下 平 移 ，若 平 移 后 ，在 四 边 形 ABEC 中 满 足 S △BCE = S△ABC，求此 时直线 的解析式； (Ⅲ)将(Ⅰ)中的抛物线作适当的平移，若平移后，在四边形 ABEC 中满足 S△BCE = 2S△AOC，且顶点 恰好落在直线 上，求此时抛物线的解析式. 解：(Ⅰ)当 ， 时，抛物线的解析式为 ，即 . ∴ 抛物线顶点 的坐标为(1，4)． ．．．．．．．．．．．．．．．．．2 分 (Ⅱ)将(Ⅰ)中的抛物线向下平移，则顶点 在对称轴 上，有 ， ∴ 抛物线的解析式为 ( )． ∴ 此时，抛物线与 轴的交点为 ，顶点为 ． ∵ 方程 的两个根为 ， ， ∴ 此时，抛物线与 轴的交点为 ， ． 如图，过点 作 EF∥CB 与 轴交于点 ，连接 ，则 S△BCE = S△BCF． ∵ S△BCE = S△ABC， ∴ S△BCF = S△ABC． ∴ ． 设对称轴 与 轴交于点 ， 则 ． 由 EF∥CB，得 ． ∴ Rt△EDF∽Rt△COB．有 ． ∴ ．结合题意，解得 ． ∴ 点 ， ． 设直线 的解析式为 ，则 2y x bx c= − + + x A B A B y C E 2b = 3c = E BC E 4 3y x= − + 2b = 3c = 2 2 3y x x= − + + 2( 1) 4y x= − − + E E 1x = 2b = 2 2y x x c= − + + 0c > y 0( )C c， 1( 1 )E c+， 2 2 0x x c− + + = 1 1 1x c= − + 2 1 1x c= + + x 1 1 0( )A c− + ， 1 1 0( )B c+ + ， E x F CF 2 1BF AB c= = + 1x = x D 1 3 12DF AB BF c= + = + EFD CBO∠ = ∠ ED CO DF OB = 1 3 1 1 1 c c c c + = + + + 5 4c = 5 4( 0 )C ， 5 2( 0)B ， BC y mx n= + 解得 ∴ 直线 的解析式为 . ．．．．．．．．．．．．．．．．．．．．．6 分 (Ⅲ)根据题意，设抛物线的顶点为 ，( ， ) 则抛物线的解析式为 ， 此时，抛物线与 轴的交点为 ， 与 轴的交点为 ， .( ) 过点 作 EF∥CB 与 轴交于点 ，连接 ， 则 S△BCE = S△BCF. 由 S△BCE = 2S△AOC， ∴ S△BCF = 2S△AOC. 得 . 设该抛物线的对称轴与 轴交于点 . 则 . 于是，由 Rt△EDF∽Rt△COB，有 ． ∴ ，即 ． 结合题意，解得 ． ① ∵ 点 在直线 上，有 ． ② ∴ 由①②，结合题意，解得 ． 有 ， ．∴ 抛物线的解析式为 ． ．．．．．．．．．．10 分 4.(2011·天津)已知抛物线 ： ．点 F(1，1)． (Ⅰ) 求抛物线 的顶点坐标； (Ⅱ) ①若抛物线 与 y 轴的交点为 A．连接 AF，并延长交抛物线 于点 B，求证： ②抛物线 上任意一点 P( ))( )．连接 PF．并延长交抛物线 于点 Q( )， 5 ,4 50 .2 n m n  =  = + 1 ,2 5.4 m n  = −  = BC 1 5 2 4y x= − + ( )E h k， 0h > 0k > 2( )y x h k= − − + y 2( 0 )C h k− +， x 0( )A h k− ， 0( )B h k+ ， 0k h> > E x F CF 2 2( )BF AO k h= = − x D 1 3 22DF AB BF k h= + = − ED CO DF OB = 2 3 2 k h k k h h k − += − + 22 5 2 0h kh k− + = 1 2h k= ( )E h k， 4 3y x= − + 4 3k h= − + 1k = 1k = 1 2h = 2 3 4y x x= − + + 1C 2 1 1 12y x x= − + 1C 1C 1C 1 1 2AF BF + = 1C P Px y， 0 1Px< < 1C Q Qx y， A B O Q NF M P x y 试判断 是否成立？请说明理由； (Ⅲ) 将抛物线 作适当的平移．得抛物线 ： ，若 时． 恒成立， 求 m 的最大值． 解 (I)∵ ， ∴抛物线 的顶点坐标为( )． (II)①根据题意，可得点 A(0，1)， ∵F(1，1)． ∴AB∥x 轴．得 AF=BF=1， ② 成立． 理由如下： 如图，过点 P( )作 PM⊥AB 于点 M，则 FM= ，PM= ( ) ∴Rt△PMF 中，由勾股定理，得 又点 P( )在抛物线 上， 得 ，即 ∴ 即 ． 过点 Q( )作 QN⊥AB，与 AB 的延长线交于点 N， 同理可得 ． 图文∠PMF=∠QNF=90°，∠MFP=∠NFQ， ∴△PMF∽△QNF 有 这里 ， 1 1 2PF QF + = 1C 2C 2 2 1 ( )2y x h= − 2 x m< ≤ 2y x≤ 2 2 1 1 1 11 ( 1)2 2 2y x x x= − + = − + 1C 11 2 ， 1 1 2AF BF + = 1 1 2PF QF + = P Px y， 1 Px− 1 Py− 0 1Px< < 2 2 2 2 2(1 ) (1 )P PPF FM PM x y= + = − + − P Px y， 1C 21 1( 1)2 2P Py x= − + 2( 1) 2 1P Px y− = − 2 2 22 1 (1 )P P PPF y y y= − + − = PPF y= Q Qx y， QQF y= PF PM QF QN = 1 1PPM y PF= − = − 1 1QQN y QF= − = − x0O y3=x C2 2 x y x0′ ∴ 即 (Ⅲ) 令 ， 设其图象与抛物线 交点的横坐标为 ，x0′，且 < x0′， ∵抛物线 可以看作是抛物线 左右平移得到的， 观察图象．随着抛物线 向右不断平移， ，x0′ 的值不断增大， ∴当满足 ，． 恒成立时，m 的最大值在 x0′ 处取得. 可得当 时．所对应的 x0′ 即为 m 的最大值． 于是，将 带入 ， 有 解得 或 (舍) ∴ 此时， ，得 解得 ，x0′=8 ∴m 的最大值为 8. 5.(2012·天津)已知抛物线 y=ax2+bx+c(0＜2a＜b)的顶点为 P(x0，y0)，点 A(1，yA)、B(0，yB)、 C(–1，yC)在该抛物线上． (Ⅰ)当 a=1，b=4，c=10 时，①求顶点 P 的坐标；②求 的值； (Ⅱ)当 y0≥0 恒成立时，求 的最小值． 解：(Ⅰ)若 a=1，b=4，c=10，此时抛物线的解析式为 y=x2+4x+10. ①∵y=x2+4x+10=(x+2)2+6，∴抛物线的顶点坐标为 P(–2，6). ②∵点 A(1，yA)、B(0，yB)、C(–1，yC)在抛物线 y=x2+4x+10 上， 1 1 PF PF QF QF −= − 1 1 2PF QF + = 3y x= 2C 0x 0x 2C 21 2y x= 2C 0x 2 x m< ≤ 2y x≤ 0 2x = 0 2x = 21 ( )2 x h x− = 21 (2 ) 22 h− = 4h = 0h = 2 2 1 ( 4)2y x= − 2 3y y= 21 ( 4)2 x x− = 0 2x = A B C y y y− A B C y y y− xO y A C D E F B G x1x2 A1 –1 1 ∴yA=15，yB=10，yC=7.∴ . (Ⅱ)由 0＜2a＜b，得 . 由题意，如图过点 A 作 AA1⊥x 轴于点 A1， 则 AA1=yA，OA1=1. 连接 BC，过点 C 作 CD⊥y 轴于点 D， 则 BD=yB－yC，CD=1. 过点 A 作 AF∥BC，交抛物线于点 E(x1，yE)， 交 x 轴于点 F(x2，0). 则∠FAA1=∠CBD.∴Rt△AFA1∽Rt△BCD. ∴ ，即 . 过点 E 作 EG⊥AA1 于点 G，易得△AEG∽△BCD. ∴ ，即 =1–x1. ∵点 A(1，yA)、B(0，yB)、C(–1，yC)、E(x1，yE)在抛物线 y=ax2+bx+c 上， ∴yA=a+b+c，yB=c，yC=a–b+c，yE=ax12+bx1+c， ∴ ，化简，得 x12+x1–2=0， 解得 x1= –2(x1=1 舍去).∵y0≥0 恒成立，根据题意，有 x2≤x1＜–1. 则 1–x2≥1–x1，即 1–x2≥3.∴ 的最小值为 3. 解法 2： (Ⅱ)解：设 m＞0，由于 b＞2a＞0，令 b=2a+m 当 y0≥0 恒成立时，应有 b2–4ac≤0 ∴(2a+m)2–4ac≤0 ∵a＞0 ∴c≥ = –2m+2m= +2m ∵ ≥0 ∴c≥2m 15 510 7 A B C y y y = =− − 0 12 bx a = − −＜ 1 1AA FA BD CD = 2 2 1 11 A B C y x xy y −= = −− AG EG BD CD = A E B C y y y y − − 2 1 1 1 ( ) ( ) 1( ) a b c ax bx c xc a b c + + − + + = −− − + A B C y y y− 2(2 ) 4 a m a + 2(2 ) 4 a m a + 2(2 ) 4 a m a − 2(2 ) 4 a m a − ∵点 A(1,yA)、B(0,yB)、C(–1,yC)在抛物线 y=ax2+bx+c 上 ∴yA=a+b+c, yB=c, yC= a–b+c ∴ = = 代入 b=2a+m,得 = = = ∵c≥2m, ∴ = ≥ =3 ∴ 的最小值为 3 解法 3： A(1,a+b+c)、B(0,c)、C(–1,a–b+c) 由 B(0,c)、C(–1,a–b+c)得直线 BC 为 y=(b–a)x+c ∵AE∥BC ∴设直线 AE 为 y=(b–a)x+m 将 A(1,a+b+c)代入上式，得 m=2a+c. ∴直线 AE 为 y=(b–a)x+2a+c 由 得 x2+x–2=0. 解得 E 点横坐标为 x1=–2(x1=1 舍去) ∵y0≥0 恒成立，根据题意，有 x2≤x1＜－1. 则 1－x2≥1－x1，即 1－x2≥3.∴ 的最小值为 3. 6.(2013·天津)已知抛物线 y1=ax2+bx+c(a≠0)的对称轴是直线 l，顶点为点 M．若自变量 x 和函数值 y1 的部分对应值如下表所示： (Ⅰ)求 y1 与 x 之间的函数关系式； (Ⅱ)若经过点 T(0，t)作垂直于 y 轴的直线 l′，A 为直线 l′上的动点，线段 AM 的垂直平分线交直线 l 于点 B，点 B 关于直线 AM 的对称点为 P，记 P(x，y2)． (1)求 y2 与 x 之间的函数关系式； (2)当 x 取任意实数时，若对于同一个 x，有 y1＜y2 恒成立，求 t 的取值范围． x … –1 0 3 … y1=ax2+bx+c … 0 0 … A B C y y y− ( ) a b c c a b c + + − − + a b c b a + + − A B C y y y− 2 2 a a m c a m a + + + + − 2a m a c a m + + + + 21 a c a m ++ + A B C y y y− 21 a c a m ++ + 2 21 a m a m ++ + A B C y y y− ( ) 2 – 2y b a x a c y ax bx c  = + + = + + A B C y y y− 9 4 A B C O T L PQ M l x y l′ A B C O T L PQ M l x y l′ 解：(Ⅰ)∵抛物线经过点(0， )， ∴c= ． ∴y1=ax2+bx+ ， ∵点(–1，0)、(3，0)在抛物线 y1=ax2+bx+ 上， ∴ ，解得， ∴y1 与 x 之间的函数关系式为：y1= – x2+ x+ ； (II)∵y1= – x2+ x+ ， ∴y1= – (x–1)2+3， ∴直线 l 为 x=1，顶点 M(1，3)． ①由题意得，t≠3， 如图，记直线 l 与直线 l′交于点 C(1，t)，当点 A 与点 C 不重合时， ∵由已知得，AM 与 BP 互相垂直平分， ∴四边形 ANMP 为菱形， ∴PA∥l， 又∵点 P(x，y2)， ∴点 A(x，t) (x≠1)， ∴PM=PA=|y2–t|， 过点 P 作 PQ⊥l 于点 Q，则点 Q(1，y2)， ∴QM=|y2–3|，PQ=AC=|x–1|， 在 Rt△PQM 中， ∵PM2=QM2+PQ2，即(y2–t)2=(y2–3)2+(x–1)2，整理得，y2= (x–1)2+ ， 即 y2= x2– x+ ， ∵当点 A 与点 C 重合时，点 B 与点 P 重合， ∴P(1， )， ∴P 点坐标也满足上式， 9 4 9 4 9 4 9 4 9 04 99 3 04 a b a b  − + =  + + = 3 4 3 2 a b  = −  = 3 4 3 2 9 4 3 4 3 2 9 4 3 4 1 6 2t− 3 2 t + 1 6 2t− 1 3 t− 210 6 2 t t − − 3 2 t + A B C O T L PQ M l x y l′ A F M E O P x y 1 ∴y2 与 x 之间的函数关系式为 y2= x2– x+ (t≠3)； ②根据题意，借助函数图象： 当抛物线 y2 开口方向向上时，6–2t＞0，即 t＜3 时，抛物线 y1 的顶点 M(1，3)，抛物线 y2 的顶点(1， )， ∵3＞ ， ∴不合题意， 当抛物线 y2 开口方向向下时，6–2t＜0，即 t＞3 时， y1–y2= – (x–1)2+3–[ (x–1)2+ ] = (x–1)2+ ， 若 3t–11≠0，要使 y1＜y2 恒成立， 只要抛物线 y= (x–1)2+ 开口方向向下，且顶点(1， )在 x 轴下方， ∵3–t＜0，只要 3t–11＞0，解得 t＞ ，符合题意； 若 3t–11=0，y1–y2= – ＜0，即 t= 也符合题意． 综上，可以使 y1＜y2 恒成立的 t 的取值范围是 t≥ ． 7.(2014·天津) 在平面直角坐标系中，O 为原点，直线 l：x=1，点 A(2，0)，点 E、点 F、点 M 都在直线 l 上，且点 E 和点 F 关于点 M 对称，直线 EA 与直线 OF 交于点 P. (Ⅰ)若点 M 的坐标为(1，–1). ① 当点 F 的坐标为(1，1)时，如图，求点 P 的坐标； ② 当点 F 为直线 l 上的动点时，记点 P(x，y)，求 y 关于 x 的函数解析式； (Ⅱ)若点 M (1，m)，点 F(1，t)，其中 t ≠0.过点 P 作 PQ⊥l 于点 Q，当 OQ＝PQ 时，试用含 t 的式子表示 m. 1 6 2t− 1 3 t− 210 6 2 t t − − 3 2 t + 3 2 t + 3 4 1 6 2t− 3 2 t + 3 11 4(3 ) t t − − 3 2 t− 3 11 4(3 ) t t − − 3 2 t− 3 2 t− 11 3 1 3 11 3 11 3 解：(Ⅰ) ①∵点 O(0,0),点 F(1,1). ∴直线 OF 的解析式为 y=x 设直线 EA 的解析式为 y=kx+b 由点 E 和点 F 关于点 M(1,–1)对称，得点 E(1,–3) 又点 A(2,0).点 E 在直线 EA 上. ∴ 解得 ∴直线 EA 的解析式为 y=3x–6 ∵点 P 是直线 OF 与直线 EA 的交点， 有 .解得 ∴点 P 坐标为(3,3) ②由已知，设点 F(1,t) ∴直线 OF 的解析式为 y=tx 设直线 EA 的解析式为 y=kx+b 由点 E 和点 F 关于点 M(1，–1)对称，得点 E(1,–2–t) 又点 A、点 E 在直线 EA 上 ∴ 解得 ∴直线 EA 的解析式为 y=(2+t)x–2(2+t) ∵点 P 为直线 OF 与直线 EA 的交点 ∴tx=(2+t)x–2(2+t)，化简，得 t=x–2 有 y=tx=(x–2)x=x2–2x ∴y 关于 x 的函数解析式为 y=x2–2x (Ⅱ)根据题意，同(Ⅰ)可得 直线 OF 的解析式为 y=tx 直线 EA 的解析式为 y=(t–2m)x–2(t–2m) ∵点 P 为直线 OF 与直线 EA 的交点 ∴tx=(t–2m)x–2(t–2m)，m≠0 化简，得 . 有 y=tx= ∴点 P 坐标为( , ) 2 0 3 k b k b + =  + = − 3 6 k b =  = − 3 6 y x y x =  = − 3 3 x y =  = 2 0 2 k b k b t + =  + = − − 2 2(2 ) k t b t = +  = − + 2 tx m = − 2 2 tt m − 2 t m − 2 2 tt m − ∵PQ⊥l 于点 Q，点 Q(1, ) ∴OQ2= ，PQ2= ∵OQ=PQ ∴ = 化简，得 t(t–2m)(t2–2mt–1)=0. 又 t≠0 ∴t–2m=0 或 t2–2mt–1=0 ∴m= 或 即为所求. 8.(2015·天津)已知二次函数 y=x2+bx+c(b，c 为常数)． (Ⅰ)当 b=2，c= –3 时，求二次函数的最小值； (Ⅱ)当 c=5 时，若在函数值 y=l 的情况下，只有一个自变量 x 的值与其对应，求此时二次函数的解析 式； (Ⅲ)当 c=b2 时，若在自变量 x 的值满足 b≤x≤b+3 的情况下，与其对应的函数值 y 的最小值为 21， 求此时二次函数的解析式． 解：(Ⅰ)当 b=2，c= –3 时，二次函数的解析式为 y=x2+2x–3=(x+1)2–4， ∴当 x= –1 时，二次函数取得最小值–4； (Ⅱ)当 c=5 时，二次函数的解析式为 y=x2+bx+5， 由题意得，x2+bx+5=1 有两个相等是实数根， ∴△=b2–16=0， 解得，b1=4，b2= –4， ∴次函数的解析式 y=x2+4x+5，y=x2–4x+5； (Ⅲ)当 c=b2 时，二次函数解析式为 y=x2+bx+b2， 图象开口向上，对称轴为直线 x= – b 2， ①当– b 2＜b，即 b＞0 时， 在自变量 x 的值满足 b≤x≤b+3 的情况下，y 随 x 的增大而增大， ∴当 x=b 时，y=b2+b•b+b2=3b2 为最小值， ∴3b2=21，解得，b1= – 7(舍去)，b2= 7； ②当 b≤– b 2≤b+3 时，即–2≤b≤0， ∴x= – b 2，y= 3 4b2 为最小值， ∴ 3 4b2=21，解得，b1= –2 7(舍去)，b2=2 7(舍去)； 2 2 tt m − 2 21 (2 )tt m + − 2(1 )t m − 2 21 (2 )tt m + − 2(1 )t m − 2 t 2 1 2 tm t −= ③当– b 2＞b+3，即 b＜–2， 在自变量 x 的值满足 b≤x≤b+3 的情况下，y 随 x 的增大而减小， 故当 x=b+3 时，y=(b+3)2+b(b+3)+b2=3b2+9b+9 为最小值， ∴3b2+9b+9=21．解得，b1=1(舍去)，b2=﹣4； ∴b= 7时，解析式为：y=x2+ 7x+7 b= –4 时，解析式为：y=x2–4x+16． 综上可得，此时二次函数的解析式为 y=x2+ 7x+7 或 y=x2–4x+16． 本题考查了二次函数的最值：当 a＞0 时，抛物线在对称轴左侧，y 随 x 的增大而减少；在对称 轴右侧，y 随 x 的增大而增大，因为图象有最低点，所以函数有最小值，当 x= – b 2a时，y= 4ac–b2 4a ； 当 a＜0 时，抛物线在对称轴左侧，y 随 x 的增大而增大；在对称轴右侧，y 随 x 的增大而减少，因 为图象有最高点，所以函数有最大值，当 x= – b 2a时，y= 4ac–b2 4a ；确定一个二次函数的最值，首先看 自变量的取值范围，当自变量取全体实数时，其最值为抛物线顶点坐标的纵坐标；当自变量取某个 范围时，要分别求出顶点和函数端点处的函数值，比较这些函数值，从而获得最值． 9.（2016 年）已知抛物线 C： 的顶点为 P，与 y 轴的交点为 Q，点 F（1， ）. （Ⅰ）求点 P，Q 的坐标； （Ⅱ）将抛物线 C 向上平移得到抛物线 C′，点 Q 平移后的对应点为 Q′，且 FQ′＝OQ′. ③ 求抛物线 C′的解析式； ④ 若点 P 关于直线 Q′F 的对称点为 K，射线 FK 与抛物线 C′相交于点 A，求点 A 的坐标. 2 2 1y x x= − + 1 2 2.2 2 1.8 1.6 1.4 1.2 1 0.8 0.6 0.4 0.2 0.2 0.4 y 1 0.5 0.5 1 1.5 2 2.5 x N AK Q' F Q O P 由点 N 在直线 Q′F 上，得 ，解得 . 将 代入 ，得 . ∴点 A 的坐标为 （Ⅱ） ②解法二：设 K . 连接 Q′P、Q′K、FP. 由 P、K 关于直线 Q′F 对称，有 Q′K＝Q′P，FK＝FP，因此，Q′K 2＝Q′P 2，FK 2＝ FP 2. 根据勾股定理，得 . 解方程组，得 ，即点 K 的坐标为 . 设直线 FK 的解析式为 ，代入 F 及 K ， 得 ，解方程组得， ， 即直线 FK 的解析式为 . 点 A 为射线 FK 与抛物线 C′的交点，把 代入 ， 得方程 ，解得 . 此时， ， 即点 A 的坐标为 . 0 3 5 04 4x− + = 0 5 3x = 0 5 3x = 2 0 0 0 52 4y x x= − + 0 25 36y = 5 25( )3 36 ， 0 0( )x y， 2 2 2 2 0 0 2 2 2 0 0 5 5( ) 1 ( )4 4 1 1( 1) ( ) ( )2 2 x y x y  + − = +  − + − = 0 0 37 25 16 25 x y  =  = 37 16( )25 25 ， y kx b= + 1(1 )2 ， 37 16( )25 25 ， 1 2 37 16 25 25 k b k b  + =  + = 7 24 5 24 k b  =  = 7 5 24 24y x= + 7 5 24 24y x= + 2 52 4y x x= − + 2 55 25 024 24x x− + = 1 2 5 5 13 8x x= = <， （舍去） 25 36y = 5 25( )3 36 ， 2.2 2 1.8 1.6 1.4 1.2 1 0.8 0.6 0.4 0.2 0.2 0.4 y 0.5 0.5 1 1.5 2 2.5 3 x AK Q' F Q O P