聊城市2013年中考数学卷 8页

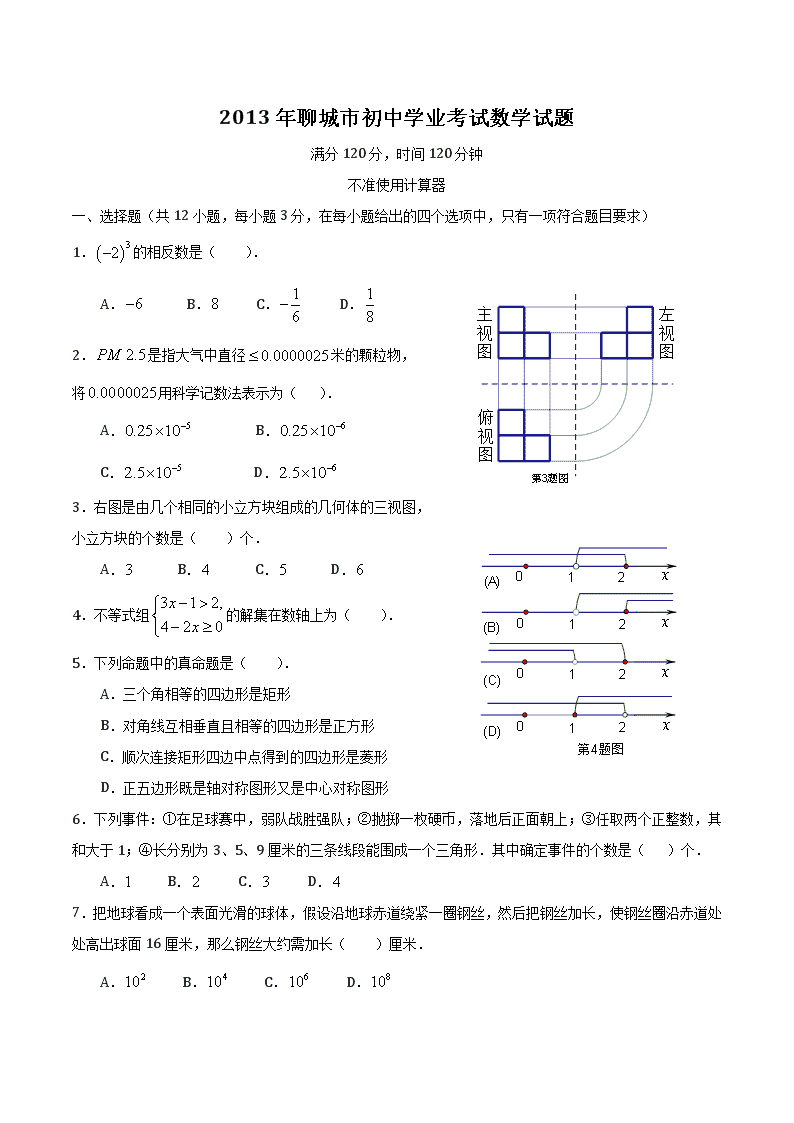
‎2013年聊城市初中学业考试数学试题 满分120分，时间120分钟 不准使用计算器 一、选择题（共12小题，每小题3分，在每小题给出的四个选项中，只有一项符合题目要求）‎ ‎1．的相反数是（ ）．Www.12999.com A． B． C． D．‎ ‎2．是指大气中直径米的颗粒物，‎ 将用科学记数法表示为（ ）．‎ A． B．‎ C． D．‎ ‎3．右图是由几个相同的小立方块组成的几何体的三视图，‎ 小立方块的个数是（ ）个．‎ A． B． C． D．‎ ‎4．不等式组的解集在数轴上为（ ）．‎ ‎5．下列命题中的真命题是（ ）．‎ A．三个角相等的四边形是矩形 B．对角线互相垂直且相等的四边形是正方形 C．顺次连接矩形四边中点得到的四边形是菱形 D．正五边形既是轴对称图形又是中心对称图形 ‎6．下列事件：①在足球赛中，弱队战胜强队；②抛掷一枚硬币，落地后正面朝上；③任取两个正整数，其和大于1；④长分别为3、5、9厘米的三条线段能围成一个三角形．其中确定事件的个数是（ ）个．‎ A． B． C． D．‎ ‎7．把地球看成一个表面光滑的球体，假设沿地球赤道绕紧一圈钢丝，然后把钢丝加长，使钢丝圈沿赤道处处高出球面16厘米，那么钢丝大约需加长（ ）厘米． ‎ A． B． C． D．‎ ‎8．二次函数的图象如图所示，那么一次函数的图象大致是（ ）．‎ ‎9．河堤横断面如图所示，堤高BC=6米，迎水坡AB的坡比为，‎ 则AB的长为（ ）米．‎ A． B． C． D．‎ ‎10．某校七年级共320名学生参加数学测试，随机抽取50名学生的成绩进行统计，其中15名学生的成绩达到优秀．估计该校七年级学生在这次数学测试中达到优秀的人数大约有（ ）人．‎ A． B． C． D．‎ ‎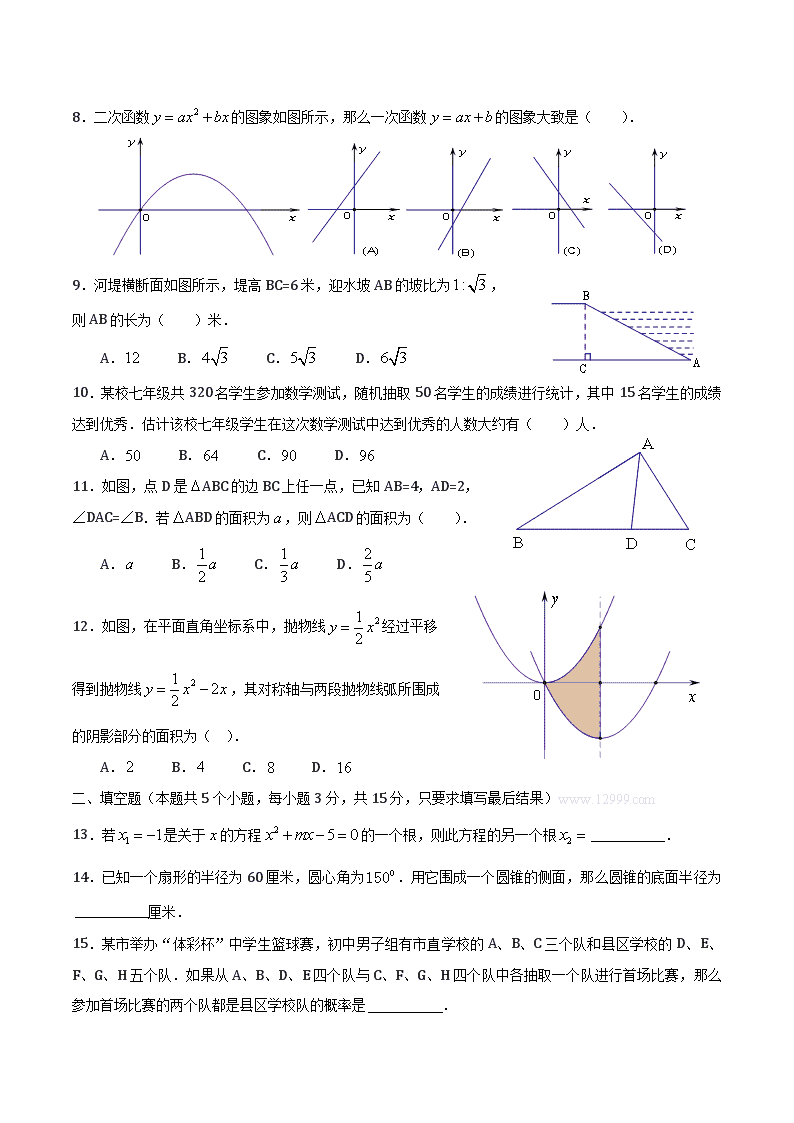11．如图，点D是ABC的边BC上任一点，已知AB=4，AD=2，‎ ‎∠DAC=∠B．若ABD的面积为，则ACD的面积为（ ）．‎ A． B． C． D．‎ ‎12．如图，在平面直角坐标系中，抛物线经过平移 得到抛物线，其对称轴与两段抛物线弧所围成 的阴影部分的面积为（ ）．‎ A． B． C． D．‎ 二、填空题（本题共5个小题，每小题3分，共15分，只要求填写最后结果）www.12999.com ‎13．若是关于的方程的一个根，则此方程的另一个根．‎ ‎14．已知一个扇形的半径为60厘米，圆心角为．用它围成一个圆锥的侧面，那么圆锥的底面半径为厘米．‎ ‎15．某市举办“体彩杯”中学生篮球赛，初中男子组有市直学校的A、B、C三个队和县区学校的D、E、F、G、H五个队．如果从A、B、D、E四个队与C、F、G、H四个队中各抽取一个队进行首场比赛，那么参加首场比赛的两个队都是县区学校队的概率是．‎ ‎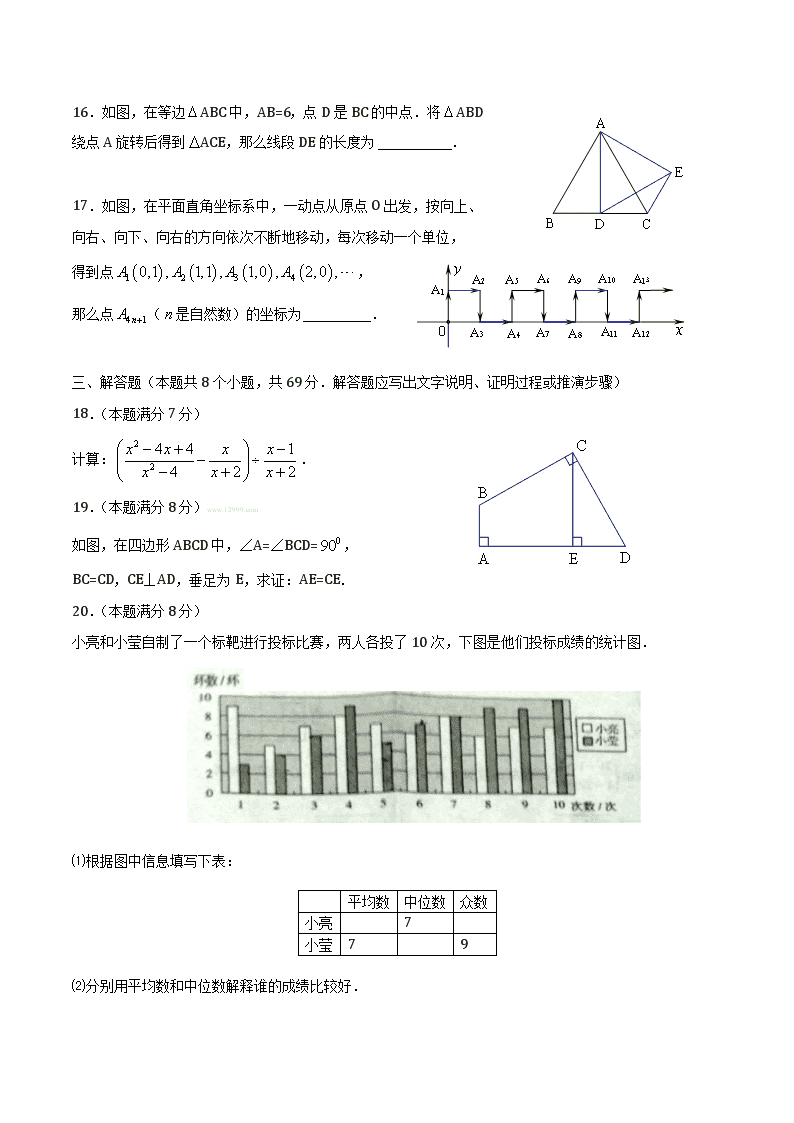16．如图，在等边ABC中，AB=6，点D是BC的中点．将ABD 绕点A旋转后得到ACE，那么线段DE的长度为．‎ ‎17．如图，在平面直角坐标系中，一动点从原点O出发，按向上、‎ 向右、向下、向右的方向依次不断地移动，每次移动一个单位，‎ 得到点，‎ 那么点（是自然数）的坐标为．‎ 三、解答题（本题共8个小题，共69分．解答题应写出文字说明、证明过程或推演步骤）‎ ‎18．（本题满分7分）‎ 计算：．‎ ‎19．（本题满分8分）www.12999.com 如图，在四边形ABCD中，∠A=∠BCD=，‎ BC=CD，CE⊥AD，垂足为E，求证：AE=CE．‎ ‎20．（本题满分8分）‎ 小亮和小莹自制了一个标靶进行投标比赛，两人各投了10次，下图是他们投标成绩的统计图．‎ 平均数 中位数 众数 小亮 ‎7‎ 小莹 ‎7‎ ‎9‎ ‎⑴根据图中信息填写下表：‎ ‎⑵分别用平均数和中位数解释谁的成绩比较好．‎ ‎21．（本题满分8分）夏季来临，天气逐渐炎热起来．某商店将某种碳酸饮料每瓶的价格上调了10%，将某种果汁饮料每瓶的价格下调了5%．已知调价前买这两种饮料各一瓶共花费7元，调价后买上述碳酸饮料3瓶和果汁饮料2瓶共花费17.5元，问这两种饮料在调价前每瓶各多少元？‎ ‎22．（本题满分8分）如图，一只猫头鹰蹲在一颗树AC的点B处，发现一只老鼠躲进短墙DF的另一侧，猫头鹰的视线被短墙遮住．为了寻找这只老鼠，猫头鹰向上飞至树顶C处．已知点B在AC上，DF=4米，短墙底部D与树的底部A的距离AD=2.7米，猫头鹰从C点观察F点的俯角为，老鼠躲藏处M距D点3米，且点M在DE上．‎ ‎（参考数据：）．‎ ‎⑴猫头鹰飞至C处后，能否看到这只老鼠？为什么？‎ ‎⑵要捕捉到这只老鼠，猫头鹰至少要飞多少米（精确到0.1米）？‎ ‎23．（本题满分8分）如图，一次函数的图象与轴、轴分别相交 于A、B两点，且与反比例函数的图象在第二象限交于点C．‎ 如果点A的坐标为，B是AC的中点．‎ ‎⑴求点C的坐标；‎ ‎⑵求一次函数的解析式．‎ ‎24．（本题满分10分）如图，AB是的直径，AF是的 切线，CD是垂直于AB的弦，垂足为E，过点C作DA的平行线 与AF相交于点F，CD=，BE=2．‎ 求证：⑴四边形FADC是菱形；‎ ‎⑵FC是的切线．‎ ‎25．（本题满分12分）已知在ABC中，边BC的长与BC边上的高的和为20．‎ ‎⑴写出ABC的面积与BC的长之间的函数关系式，并求出面积为48时BC的长；‎ ‎⑵当BC多长时，ABC的面积最大？最大面积是多少？‎ ‎⑶当ABC面积最大时，是否存在其周长最小的情形？如果存在，请说明理由，并求出其最小周长；如果不存在，请给予说明．‎ 参考答案 一、选择题：答案BDBAC BACAD CB ‎11．【解析】由已知∠DAC=∠B，∠ACD=∠BCA，∴ABC∽DAC，∴，‎ 即，∴，∴．‎ ‎12．【解析】依据平移的定义及抛物线的对称性可得：‎ 区域D的面积=区域C的面积=区域B的面积， ‎ ‎∴阴影面积=区域A的面积加上区域D的面积=正方形的面积4．‎ 二、填空题：答案 5 25 0.375 ‎ ‎13．【解析】把代入得：，由根与系数的关系得：，∴．‎ ‎14．【解析】依题意得：，解得：．‎ ‎15．【解析】依题意得：概率．‎ ‎16．【解析】依题意知：ACE≌ABD≌ACD，∴ADE是等边三角形，∴．‎ ‎17．【解析】不难发现规律：动点的横坐标每变换4次就增加2，纵坐标不变，故点的坐标为．‎ 三、解答题 ‎18．【解析】原式．‎ ‎19．【证明】连接BD、AC，∵BC=CD，∠BCD=，∴BCD是等腰直角三角形，∴∠CBD=，‎ ‎∵∠A=∠BCD=，∴A、B、C、D四点共圆，‎ ‎∴∠CAE=∠CAD=∠CBD=，‎ 又∵CE⊥AD，∴ACE是等腰直角三角形，∴AE=CE．‎ ‎【法二】作BF⊥CE于F，∵∠BCF+∠DCE=，∠D+∠DCE=，‎ ‎∴∠BCF=∠D，又BC=CD，∴RtBCF≌RtCDE，∴BF=CE，‎ 又∠BFE=∠AEF=∠A=，∴四边形ABFE是矩形，∴BF=AE，‎ 因此AE=CE．‎ 平均数 中位数 众数 小亮 ‎7‎ ‎7‎ ‎7‎ 小莹 ‎7‎ ‎7.5‎ ‎9‎ ‎20．【解析】⑴‎ ‎⑵平均数相等说明：两人整体水平相当，成绩一样好；小莹的中位数大说明：小莹的成绩比小亮好．‎ ‎21．【解析】设调价前碳酸饮料每瓶元，果汁饮料每瓶元，依题意得：www.12999.com ‎ 即 解得：‎ 答：调价前这种碳酸饮料每瓶的价格为3元，这种果汁饮料每瓶的价格为4元．‎ ‎22．【解析】⑴依题意得：∠AGC=，∠GFD=∠GCA=，‎ ‎∴DG=DF=3米=DM，因此这只猫头鹰能看到这只老鼠；‎ ‎⑵ ∵AG=AD+DG=2.7+3=5.7，∴CG=AG=9.5（米），‎ 因此猫头鹰至少要飞9.5米．‎ ‎23．【解析】⑴作CD⊥轴于D，则CD∥BO，‎ ‎∵B是AC的中点，∴O是AD的中点，∴点D的横坐标为﹣2，‎ 把代入到中，得：，‎ 因此点C的坐标为；‎ ‎⑵ 设一次函数为，由于A、C两点在其图象上，‎ ‎∴ 解得：‎ 因此一次函数的解析式为．‎ ‎24．【证明】⑴连接OC，‎ 依题意知：AF⊥AB，又CD⊥AB，∴AF∥CD，‎ 又CD∥AD，∴四边形FADC是平行四边形，‎ 由垂径定理得：CE=ED=，www.12999.com 设的半径为R，则OC=R，OE=OB﹣BE=R﹣2，‎ 在ECO中，由勾股定理得：，解得：R=4，‎ ‎∴AD=，∴AD=CD，‎ 因此平行四边形FADC是菱形；‎ ‎⑵ 连接OF，由⑴得：FC=FA，又OC=OA，FO=FO，‎ ‎∴FCO≌FAO，∴∠FCO=∠FAO=，‎ 因此FC是的切线．‎ ‎25．【解析】⑴依题意得：，‎ 解方程得：，∴当ABC面积为48时BC的长为12 或8；‎ ‎⑵ 由⑴得：，www.12 999.com ‎∴当即BC=10时，ABC的面积最大，最大面积是50；‎ ‎⑶ABC的周长存在最小的情形，理由如下：‎ 由⑵可知ABC的面积最大时，BC=10，BC边上的高也为10，‎ 过点A作直线L平行于BC，作点B关于直线L的对称点，‎ 连接交直线L于点，再连接，‎ 则由对称性得：，‎ ‎∴，‎ 当点A不在线段上时，则由三角形三边关系可得：‎ ‎，‎ 当点A在线段上时，即点A与重合，这时，‎ 因此当点A与重合时，ABC的周长最小；‎ 这时由作法可知：，∴，∴，‎ 因此当ABC面积最大时，存在其周长最小的情形，最小周长为．‎