- 1000.21 KB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
特殊四边形综合题
1.如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.
2.已知在矩形ABCD中,∠ADC的平分线DE与BC边所在的直线交于点E,点P是线段DE上一定点(其中EP<PD)
(1)如图1,若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交射线DA于点H、G.
①求证:PG=PF; ②探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.
(2) 拓展:如图2,若点F在CD的延长线上(不与D重合),过点P作PG⊥PF,交射线DA于点G,你认为(1)中DF、DG、DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.
3.已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与
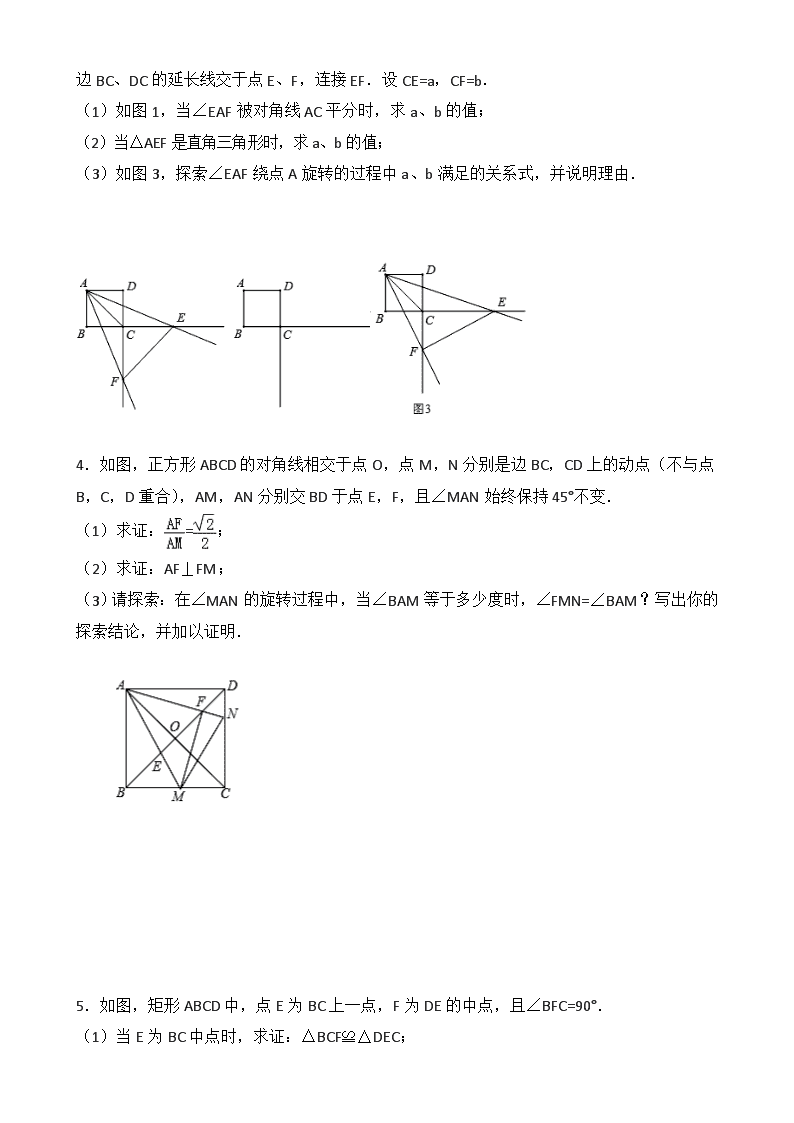
边BC、DC的延长线交于点E、F,连接EF.设CE=a,CF=b.
(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;
(2)当△AEF是直角三角形时,求a、b的值;
(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由.
4.如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.
(1)求证:=;
(2)求证:AF⊥FM;
(3)请探索:在∠MAN的旋转过程中,当∠BAM等于多少度时,∠FMN=∠BAM?写出你的探索结论,并加以证明.
5.如图,矩形ABCD中,点E为BC上一点,F为DE的中点,且∠BFC=90°.
(1)当E为BC中点时,求证:△BCF≌△DEC;
(2)当BE=2EC时,求的值;
(3)设CE=1,BE=n,作点C关于DE的对称点C′,连结FC′,AF,若点C′到AF的距离是,求n的值.
6.如图1,在菱形ABCD中,AB=6,tan∠ABC=2,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.
(1)求证:BE=DF;
(2)当t= 秒时,DF的长度有最小值,最小值等于 ;
(3)如图2,连接BD、EF、BD交EC、EF于点P、Q,当t为何值时,△EPQ是直角三角形?
(4)如图3,将线段CD绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CG.在点E的运动过程中,当它的对应点F位于直线AD上方时,直接写出点F到直线AD的距离y关于时间t的函数表达式.
7.已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
8.如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.
(1)求证:BG=AE;
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)
①求证:BG⊥GE;
②设DG与AB交于点M,若AG:AE=3:4,求的值.
9.如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.
10.如图(1)矩形ABCD中,AB=2,BC=5,BP=1,∠MPN=90°将∠MPN绕点P从PB处开始按顺时针方向旋转,PM交AB(或AD)于点E,PN交边AD(或CD)于点F,当PN旋转至PC处时,∠MPN的旋转随即停止
(1)特殊情形:如图(2),发现当PM过点A时,PN也恰好过点D,此时,△ABP ∽ △PCD(填:“≌”或“~”
(2)类比探究:如图(3)在旋转过程中,的值是否为定值?若是,请求出该定值;若不是,请说明理由;
(3)拓展延伸:设AE=t,△EPF面积为S,试确定S关于t的函数关系式;当S=4.2时,求所对应的t的值.
11.已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为点E、F,点O为AC的中点.
(1)当点P与点O重合时如图1,易证OE=OF(不需证明)
(2)直线BP绕点B逆时针方向旋转,当∠OFE=30°时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3
的猜想,并选择一种情况给予证明.
12.如图,在正方形ABCD中,点E为对角线AC上的一点,连接BE,DE.
(1)如图1,求证:△BCE≌△DCE;
(2)如图2,延长BE交直线CD于点F,G在直线AB上,且FG=FB.
①求证:DE⊥FG;
②已知正方形ABCD的边长为2,若点E在对角线AC上移动,当△BFG为等边三角形时,求线段DE的长(直接写出结果,不必写出解答过程).
13.如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
14.如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)探究线段EG、GF、AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2,求BE的长.
15.如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3时,求线段DH的长.
16.如图1,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD、BC分别交于点E、F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.
(1)求证:①△DOK≌△BOG;②AB+AK=BG;
(2)若KD=KG,BC=4﹣.
①求KD的长度;
②如图2,点P是线段KD上的动点(不与点D、K重合),PM∥DG交KG于点M,PN∥KG交DG于点N,设PD=m,当S△PMN=时,求m的值.
17.已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
18.在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
(1)当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
19.已知菱形ABCD的边长为1,∠ADC=60°,等边△AEF两边分别交DC、CB于点E、F.
(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点,求证:菱形ABCD对角线AC、BD的交点O即为等边△AEF的外心;
(2)若点E、F始终分别在边DC、CB上移动,记等边△AEF的外心为P. ①猜想验证:如图2,猜想△AEF的外心P落在哪一直线上,并加以证明;②拓展运用:如图3,当E、F分别是边DC、CB的中点时,过点P任作一直线,分别交DA边于点M,BC边于点G,DC
边的延长线于点N,请你直接写出的值.
20.在正方形ABCD中,BD是一条对角线,点E在直线CD上(与点C,D不重合),连接AE,平移△ADE,使点D移动到点C,得到△BCF,过点F作FG⊥BD于点G,连接AG,EG.
(1)问题猜想:如图1,若点E在线段CD上,试猜想AG与EG的数量关系是 ,位置关系是 ;
(2)类比探究:如图2,若点E在线段CD的延长线上,其余条件不变,小明猜想(1)中的结论仍然成立,请你给出证明;
(3)解决问题:若点E在线段DC的延长线上,且∠AGF=120°,正方形ABCD的边长为2,请在备用图中画出图形,并直接写出DE的长度.
21.如图,正方形ABCD边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG=2时,
求证:菱形EFGH为正方形;
(3)设AH=x,DG=2x,△FCG的面积为y,试求y的最大值.
22.如图1,四边形ABCD中,AD∥BC,AB⊥BC,点E在边AB上,∠DEC=90°,且DE=EC.
(1)求证:△ADE≌△BEC;
(2)若AD=a,AE=b,DE=c,请用图1证明勾股定理:a2+b2=c2;
(3)线段AB上另有一点F(不与点E重合),且DF⊥CF(如图2),若AD=2,BC=4,求EF的长.
23.如图1,正方形ABCD中,AC是对角线,等腰Rt△CMN中,∠CMN=90°,CM=MN,点M在CD边上,连接AN,点E是AN的中点,连接BE.
(1)若CM=2,AB=6,求AE的值;
(2)求证:2BE=AC+CN;
(3)当等腰Rt△CMN的点M落在正方形ABCD的BC边上,如图2,连接AN,点E是AN的中点,连接BE,延长NM交AC于点F.请探究线段BE、AC、CN的数量关系,并证明你的结论.
24.正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.
(1)如图1,若点E是DC的中点,CH与AB之间的数量关系是 ;
(2)如图2,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
(3)如图3,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.
25.问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40
(﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:=1.41,=1.73)
26.如图1,正方形OABC与正方形ODEF放置在直线l上,连结AD、CF,此时AD=CF.AD⊥CF成立.
(1)正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?若成立,请证明;若不成立,请说明理由.
(2)正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,求证:AD⊥CF.
(3)在(2)小题的条件下,AD与OC的交点为G,当AO=3,OD=时,求线段CG的长.
27.如图,在正方形ABCD与等腰直角三角形BEF中,∠BEF=90°,BE=EF,连接PF,点P是FD的中点,连接PE、PC.
(1)如图1,当点E在CB边上时,
求证:PE=CE;
(2)如图2,当点E在CB的延长线上时,线段PC、CE有怎样的数量关系,写出你的猜想,并给与证明.
28.已知:l1∥l2∥l3∥l4,平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”.
(1)如图1,正方形ABCD为“格线四边形”,则正方形ABCD的边长为 .
(2)矩形ABCD为“格线四边形”,其长:宽=2:1,求矩形ABCD的宽.
(3)如图1,EG过正方形ABCD的顶点D且垂直l1于点E,分别交l2,l4于点F,G.将∠AEG绕点A顺时针旋转30°得到∠AE′D′(如图2),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′,C′分别在直线l2,l4上,求菱形AB′C′D′的边长.
29.正方形ABCD边长为4cm,点E,M分别是线段AC,CD上的动点,连接DE并延长,交正方形ABCD的边于点F,过点M作MN⊥DF于H,交AD于N.
(1)如图1,若点M与点C重合,
求证:DF=MN;
(2)如图2,若点M从点C出发,以1cm/s的速度沿CD向点D运动,点E同时从点A出发,以cm/s速度沿AC向点C运动,运动时间为t(t>0);
①当点F是边AB的中点时,求t的值;
②连结FM,FN,当t为何值时△MNF是等腰三角形(直接写出t值).
30.已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边长分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.
(1)如图①,当∠MAN点A旋转到BM=DN时,请你直接写出AH与AB的数量关系: ;
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;
(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.
特殊四边形综合题答案
1.如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.
解:(1)四边形APQD为平行四边形;
(2)OA=OP,OA⊥OP,理由如下:
∵四边形ABCD是正方形,
∴AB=BC=PQ,∠ABO=∠OBQ=45°,
∵OQ⊥BD, ∴∠PQO=45°,
∴∠ABO=∠OBQ=∠PQO=45°,∴OB=OQ,
在△AOB和△OPQ中,
∴△AOB≌△POQ(SAS),
∴OA=OP,∠AOB=∠POQ,
∴∠AOP=∠BOQ=90°,
∴OA⊥OP;
(3)如图,过O作OE⊥BC于E.
①如图1,当P点在B点右侧时,
则BQ=x+2,OE=,
∴y=וx,即y=(x+1)2﹣,
又∵0≤x≤2,
∴当x=2时,y有最大值为2;
②如图2,当P点在B点左侧时,
则BQ=2﹣x,OE=,
∴y=וx,即y=﹣(x﹣1)2+,
又∵0≤x≤2,
∴当x=1时,y有最大值为;
综上所述,∴当x=2时,y有最大值为2;
2.已知在矩形ABCD中,∠ADC的平分线DE与BC边所在的直线交于点E,点P是线段DE上一定点(其中EP<PD)
(1)如图1,若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交射线DA于点H、G.
①求证:PG=PF; ②探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.
(2)拓展:如图2,若点F在CD的延长线上(不与D重合),过点P作PG⊥PF,交射线DA于点G,你认为(1)中DF、DG、DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.
【分析】(1)①若证PG=PF,可证△HPG≌△DPF,已知∠DPH=∠HPG,由旋转可知∠GPF=∠HPD=90°及DE平分∠ADC得△HPD为等腰直角三角形,即∠DHP=∠PDF=45°、PD=PH,即可得证;
②由△HPD为等腰直角三角形,△HPG≌△DPF知HD=DP,HG=DF,根据DG+DF=DG+GH=DH即可得;
(2)过点P作PH⊥PD交射线DA于点H,先证△HPD为等腰直角三角形可得PH=PD,HD=DP,再证△HPG≌△DPF可得HG=DF,根据DH=DG﹣HG=DG﹣DF可得DG﹣DF=DP.
解:(1)①∵∠GPF=∠HPD=90°,∠ADC=90°,
∴∠GPH=∠FPD,
∵DE平分∠ADC,
∴∠PDF=∠ADP=45°,
∴△HPD为等腰直角三角形,
∴∠DHP=∠PDF=45°,
在△HPG和△DPF中,
∵,
∴△HPG≌△DPF(ASA),
∴PG=PF;
②结论:DG+DF=DP,
由①知,△HPD为等腰直角三角形,△HPG≌△DPF,
∴HD=DP,HG=DF,
∴HD=HG+DG=DF+DG,
∴DG+DF=DP;
(2)不成立,数量关系式应为:DG﹣DF=DP,
如图,过点P作PH⊥PD交射线DA于点H,
∵PF⊥PG,
∴∠GPF=∠HPD=90°,
∴∠GPH=∠FPD,
∵DE平分∠ADC,且在矩形ABCD中,∠ADC=90°,
∴∠HDP=∠EDC=45°,得到△HPD为等腰直角三角形,
∴∠DHP=∠EDC=45°,且PH=PD,HD=DP,
∴∠GHP=∠FDP=180°﹣45°=135°,
在△HPG和△DPF中,
∵
∴△HPG≌△DPF,
∴HG=DF,
∴DH=DG﹣HG=DG﹣DF,
∴DG﹣DF=DP.
3.已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF.设CE=a,CF=b.
(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;
(2)当△AEF是直角三角形时,求a、b的值;
(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由.
【分析】(1)当∠EAF被对角线AC平分时,易证△ACF≌△ACE,因此CF=CE,即a=b.
(2)分两种情况进行计算,①先用勾股定理得出CF2=8(CE+4)①,再用相似三角形得出4CF=CE(CE+4)②,两式联立解方程组即可;
(3)先判断出∠AFD=∠CEF,再判断出AF=EF,从而得到△ADF≌△FCE即可.
解:(1)∵四边形ABCD是正方形,
∴∠BCF=∠DCE=90°
∵AC是正方形ABCD的对角线,
∴∠ACB=∠ACD=45°,
∴∠ACF=∠ACE,
∵∠EAF被对角线AC平分,
∴∠CAF=∠CAE,
在△ACF和△ACE中,
,
∴△ACF≌△ACE,
∴CE=CE,
∵CE=a,CF=b,
∴a=b,
∵△ACF≌△ACE,
∴∠AEF=∠AFE,
∵∠EAF=45°,
∴∠AEF=∠AFE=67.5°,
∵CE=CF,∠ECF=90°,∠AEC=∠AFC=22.5°,
∵∠CAF=∠CAE=22.5°,
∴∠CAE=∠CEA,
∴CE=AC=4,
即:a=b=4;
(2)当△AEF是直角三角形时,
①当∠AFE=90°时,∴∠AFD+∠CFE=90°,
∵∠CEF+∠CFE=90°,
∴∠AFD=∠CEF
∵∠AFE=90°,∠EAF=45°,
∴∠AEF=45°=∠EAF
∴AF=EF,
在△ADF和△FCE中
∴△ADF≌△FCE,
∴FC=AD=4,CE=DF=CD+FC=8,
∴a=8,b=4
②当∠AEF=90°时,
同①的方法得,CF=4,CE=8,
∴a=4,b=8.
(3)ab=32,
理由:如图,
∵AB∥CD
∴∠BAG=∠AFC,
∵∠BAC=45°,
∴∠BAG+∠CAF=45°,
∴∠AFC+∠CAF=45°,
∵∠AFC+∠AEC=180°﹣(∠CFE+∠CEF)﹣∠EAF=180°﹣90°﹣45°=45°,
∴∠CAF=∠AEC,
∵∠ACF=∠ACE=135°,
∴△ACF∽△ECA,
∴,
∴EC×CF=AC2=2AB2=32
∴ab=32.
4.(2016•淄博)如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.
(1)求证:=;
(2)求证:AF⊥FM;
(3)请探索:在∠MAN的旋转过程中,当∠BAM等于多少度时,∠FMN=∠BAM?写出你的探索结论,并加以证明.
【分析】(1)先证明A、B、M、F四点共圆,根据圆内接四边形对角互补即可证明∠AFM=90°,根据等腰直角三角形性质即可解决问题.
(2)由(1)的结论即可证明.
(3)由:A、B、M、F四点共圆,推出∠BAM=∠EFM,因为∠BAM=∠FMN,所以∠EFM=∠FMN,推出MN∥BD,得到=,推出BM=DN,再证明△ABM≌△ADN即可解决问题.
(1)证明:∵四边形ABCD是正方形,
∴∠ABD=∠CBD=45°,∠ABC=90°,
∵∠MAN=45°,
∴∠MAF=∠MBE,
∴A、B、M、F四点共圆,
∴∠ABM+∠AFM=180°,
∴∠AFM=90°,
∴∠FAM=∠FMA=45°,
∴AM=AF,
∴=.
(2)由(1)可知∠AFM=90°,
∴AF⊥FM.
(3)结论:∠BAM=22.5时,∠FMN=∠BAM
理由:∵A、B、M、F四点共圆,
∴∠BAM=∠EFM,
∵∠BAM=∠FMN,
∴∠EFM=∠FMN,
∴MN∥BD,
∴=,∵CB=DC,
∴CM=CN,
∴MB=DN,
在△ABM和△ADN中,
,
∴△ABM≌△ADN,
∴∠BAM=∠DAN,
∵∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠BAM=22.5°.
5.(2016•丽水)如图,矩形ABCD中,点E为BC上一点,F为DE的中点,且∠BFC=90°.
(1)当E为BC中点时,求证:△BCF≌△DEC;
(2)当BE=2EC时,求的值;
(3)设CE=1,BE=n,作点C关于DE的对称点C′,连结FC′,AF,若点C′到AF的距离是,求n的值.
【分析】(1)由矩形和直角三角形斜边上的中线性质得出CF=DE=EF,由等腰三角形的性质得出∠FEC=∠FCE,证出CF=CE,由ASA证明△BCF≌△DEC即可;
(2)设CE=a,则BE=2a,BC=3a,证明△BCF∽△DEC,得出对应边成比例=,得出ED2=6a2,由勾股定理得出DC=a,即可得出结果;
(3)过C′作C′H⊥AF于点H,连接CC′交EF于M,由直角三角形斜边上的中线性质得出∠FEC=∠FCE,证出∠ADF=∠BCF,由SAS证明△ADF≌△BCF,得出∠AFD=∠BFC=90°,证出四边形C′MFH是矩形,得出FM=C′H=,设EM=x,则FC=FE=x+,由勾股定理得出方程,解方程求出EM=,FC=FE=+;由(2)得:,把CE=1,BE=n代入计算即可得出n的值.
(1)证明;∵在矩形ABCD中,∠DCE=90°,F是斜边DE的中点,
∴CF=DE=EF,
∴∠FEC=∠FCE,
∵∠BFC=90°,E为BC中点,
∴EF=EC,∴CF=CE,
在△BCF和△DEC中,,
∴△BCF≌△DEC(ASA);
(2)解:设CE=a,由BE=2CE,得:BE=2a,BC=3a,
∵CF是Rt△DCE斜边上的中线,
∴CF=DE,
∵∠FEC=∠FCE,∠BFC=∠DCE=90°,
∴△BCF∽△DEC,
∴=,
即:=,
解得:ED2=6a2
由勾股定理得:,
∴==;
(3)解:过C′作C′H⊥AF于点H,连接CC′交EF于M,如图所示:
∵CF是Rt△DCE斜边上的中线,
∴FC=FE=FD,
∴∠FEC=∠FCE,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴∠ADF=∠CEF,
∴∠ADF=∠BCF,
在△ADF和△BCF中,,
∴△ADF≌△BCF(SAS),
∴∠AFD=∠BFC=90°,
∵CH⊥AF,C′C⊥EF,∠HFE=∠C′HF=∠C′MF=90°,
∴四边形C′MFH是矩形,
∴FM=C′H=,
设EM=x,则FC=FE=x+,
在Rt△EMC和Rt△FMC中,
由勾股定理得:CE2﹣EM2=CF2﹣FM2,
∴12﹣x2=(x+)2﹣()2,
解得:x=,或x=﹣(舍去),
∴EM=,FC=FE=+;
由(2)得:,
把CE=1,BE=n代入上式计算得:CF=,
∴,
解得:n=4.
6.如图1,在菱形ABCD中,AB=6,tan∠ABC=2,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.
(1)求证:BE=DF;
(2)当t= 6+6 秒时,DF的长度有最小值,最小值等于 12 ;
(3)如图2,连接BD、EF、BD交EC、EF于点P、Q,当t为何值时,△EPQ是直角三角形?
(4)如图3,将线段CD绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CG.在点E的运动过程中,当它的对应点F位于直线AD上方时,直接写出点F到直线AD的距离y关于时间t的函数表达式.
【分析】(1)由∠ECF=∠BCD得∠DCF=∠BCE,结合DC=BC、CE=CF证△DCF≌△BCE即可得;
(2)当点E运动至点E′时,由DF=BE′知此时DF最小,求得BE′、AE′即可得答案;
(3)①∠EQP=90°时,由∠ECF=∠BCD、BC=DC、EC=FC得∠BCP=∠EQP=90°,根据AB=CD=6,tan∠ABC=tan∠ADC=2即可求得DE;
②∠EPQ=90°时,由菱形ABCD的对角线AC⊥BD知EC与AC重合,可得DE=6;
(4)连接GF分别角直线AD、BC于点M、N,过点F作FH⊥AD于点H,证△DCE≌△GCF可得∠3=∠4=∠1=∠2,即GF∥CD,从而知四边形CDMN是平行四边形,由平行四边形得MN=CD=6;再由∠CGN=∠DCN=∠CNG知CN=CG=CD=6,根据tan∠ABC=tan∠CGN=2可得GM=6+12,由GF=DE=t得FM=t﹣6﹣12,
利用tan∠FMH=tan∠ABC=2即可得FH.
解:(1)∵∠ECF=∠BCD,即∠BCE+∠DCE=∠DCF+∠DCE,
∴∠DCF=∠BCE,
∵四边形ABCD是菱形,
∴DC=BC,
在△DCF和△BCE中,
∵,
∴△DCF≌△BCE(SAS),
∴DF=BE;
(2)如图1,
当点E运动至点E′时,DF=BE′,此时DF最小,
在Rt△ABE′中,AB=6,tan∠ABC=tan∠BAE′=2,
∴设AE′=x,则BE′=2x,
∴AB=x=6,
则AE′=6
∴DE′=6+6,DF=BE′=12,
故答案为:6+6,12;
(3)∵CE=CF,
∴∠CEQ<90°,
①当∠EQP=90°时,如图2①,
∵∠ECF=∠BCD,BC=DC,EC=FC,
∴∠CBD=∠CEF,
∵∠BPC=∠EPQ,
∴∠BCP=∠EQP=90°,
∵AB=CD=6,tan∠ABC=tan∠ADC=2,
∴DE=6,
∴t=6秒;
②当∠EPQ=90°时,如图2②,
∵菱形ABCD的对角线AC⊥BD,
∴EC与AC重合,
∴DE=6,
∴t=6秒;
(4)y=t﹣12﹣,
如图3,连接GF分别角直线AD、BC于点M、N,过点F作FH⊥AD于点H,
由(1)知∠1=∠2,
又∵∠1+∠DCE=∠2+∠GCF,
∴∠DCE=∠GCF,
在△DCE和△GCF中,
∵,
∴△DCE≌△GCF(SAS),
∴∠3=∠4,
∵∠1=∠3,∠1=∠2,
∴∠2=∠4,
∴GF∥CD,
又∵AH∥BN,
∴四边形CDMN是平行四边形,
∴MN=CD=6,
∵∠BCD=∠DCG,
∴∠CGN=∠DCN=∠CNG,
∴CN=CG=CD=6,
∵tan∠ABC=tan∠CGN=2,
∴GN=12,
∴GM=6+12,
∵GF=DE=t,
∴FM=t﹣6﹣12,
∵tan∠FMH=tan∠ABC=2,
∴FH=(t﹣6﹣12),
即y=t﹣12﹣.
7.已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
【分析】(1)结论AE=EF=AF.只要证明AE=AF即可证明△AEF是等边三角形.
(2)欲证明BE=CF,只要证明△BAE≌△CAF即可.
(3)过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,根据FH=CF•cos30°,因为CF=BE,只要求出BE即可解决问题.
(1)解:结论AE=EF=AF.
理由:如图1中,连接AC,
∵四边形ABCD是菱形,∠B=60°,
∴AB=BC=CD=AD,∠B=∠D=60°,
∴△ABC,△ADC是等边三角形,
∴∠BAC=∠DAC=60°
∵BE=EC,
∴∠BAE=∠CAE=30°,AE⊥BC,
∵∠EAF=60°,
∴∠CAF=∠DAF=30°,
∴AF⊥CD,
∴AE=AF(菱形的高相等),
∴△AEF是等边三角形,
∴AE=EF=AF.
(2) 证明:如图2中,
∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAE,
在△BAE和△CAF中,
,
∴△BAE≌△CAF,
∴BE=CF.
(3)解:过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,
∵∠EAB=15°,∠ABC=60°,
∴∠AEB=45°,
在RT△AGB中,∵∠ABC=60°AB=4,
∴BG=2,AG=2,
在RT△AEG中,∵∠AEG=∠EAG=45°,
∴AG=GE=2,
∴EB=EG﹣BG=2﹣2,
∵△AEB≌△AFC,
∴AE=AF,EB=CF=2﹣2,
在RT△CHF中,∵∠HCF=180°﹣∠BCD=60°,CF=2﹣2,
∴FH=CF•sin60°=(2﹣2)•=3﹣.
∴点F到BC的距离为3﹣.
8.如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.
(1)求证:BG=AE;
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)
①求证:BG⊥GE;
②设DG与AB交于点M,若AG:AE=3:4,求的值.
【分析】(1)如图①,根据等腰直角三角形的性质得AD=BD,再根据正方形的性质得∠GDE=90°,DG=DE,则可根据“SAS“判断△BDG≌△ADE,于是得到BG=AE;
(2)①如图②,先判断△DEG为等腰直角三角形得到∠1=∠2=45°,再由△BDG≌△ADE得到∠3=∠2=45°,则可得∠BGE=90°,所以BG⊥GE;
②设AG=3x,则AE=4x,即GE=7x,利用等腰直角三角形的性质得DG=GE=x,由(1)的结论得BG=AE=4x,则根据勾股定理得AB=5x,接着由△ABD为等腰直角三角形得到∠4=45°,BD=AB=x,然后证明△DBM∽△DGB,则利用相似比可计算出DM=x,所以GM=x,于是可计算出的值.
(1)证明:如图①,
∵AD为等腰直角△ABC的高,
∴AD=BD,
∵四边形DEFG为正方形,
∴∠GDE=90°,DG=DE,
在△BDG和△ADE中
,
∴△BDG≌△ADE,
∴BG=AE;
(2)①证明:如图②,
∵四边形DEFG为正方形,
∴△DEG为等腰直角三角形,
∴∠1=∠2=45°,
由(1)得△BDG≌△ADE,
∴∠3=∠2=45°,
∴∠1+∠3=45°+45°=90°,即∠BGE=90°,
∴BG⊥GE;
②解:设AG=3x,则AE=4x,即GE=7x,
∴DG=GE=x,
∵△BDG≌△ADE,∴BG=AE=4x,
在Rt△BGA中,
,
∵△ABD为等腰直角三角形,
∴∠4=45°,BD=AB=x,
∴∠3=∠4,
而∠BDM=∠GDB,
∴△DBM∽△DGB,
∴BD:DG=DM:BD,即x:x=DM:x,解得DM=x,
∴GM=DG﹣DM=x﹣x=x,
∴==.
9.如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 AF=AE ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.
【分析】(1)如图①中,结论:AF=AE,只要证明△AEF是等腰直角三角形即可.
(2)如图②中,结论:AF=AE,连接EF,DF交BC于K,先证明△EKF≌△EDA再证明△AEF是等腰直角三角形即可.
(3)如图③中,结论不变,AF=AE,连接EF,延长FD交AC于K,先证明△EDF≌△ECA,再证明△AEF是等腰直角三角形即可.
解:(1)如图①中,结论:AF=AE.
理由:∵四边形ABFD是平行四边形,
∴AB=DF,
∵AB=AC,
∴AC=DF,
∵DE=EC,
∴AE=EF,
∵∠DEC=∠AEF=90°,
∴△AEF是等腰直角三角形,
∴AF=AE.
故答案为AF=AE.
(2)如图②中,结论:AF=AE.
理由:连接EF,DF交BC于K.
∵四边形ABFD是平行四边形,
∴AB∥DF,
∴∠DKE=∠ABC=45°,
∴EKF=180°﹣∠DKE=135°,EK=ED,
∵∠ADE=180°﹣∠EDC=180°﹣45°=135°,
∴∠EKF=∠ADE,
∵∠DKC=∠C,
∴DK=DC,
∵DF=AB=AC,
∴KF=AD,
在△EKF和△EDA中,
,
∴△EKF≌△EDA,
∴EF=EA,∠KEF=∠AED,
∴∠FEA=∠BED=90°,
∴△AEF是等腰直角三角形,
∴AF=AE.
(3)如图③中,结论不变,AF=AE.
理由:连接EF,延长FD交AC于K.
∵∠EDF=180°﹣∠KDC﹣∠EDC=135°﹣∠KDC,
∠ACE=(90°﹣∠KDC)+∠DCE=135°﹣∠KDC,
∴∠EDF=∠ACE,
∵DF=AB,AB=AC,
∴DF=AC
在△EDF和△ECA中,
,
∴△EDF≌△ECA,
∴EF=EA,∠FED=∠AEC,
∴∠FEA=∠DEC=90°,
∴△AEF是等腰直角三角形,
∴AF=AE.
10.如图(1)矩形ABCD中,AB=2,BC=5,BP=1,∠MPN=90°将∠MPN绕点P从PB处开始按顺时针方向旋转,PM交AB(或AD)于点E,PN交边AD(或CD)于点F,当PN旋转至PC处时,∠MPN的旋转随即停止
(1)特殊情形:如图(2),发现当PM过点A时,PN也恰好过点D,此时,△ABP ∽ △PCD(填:“≌”或“~”
(2)类比探究:如图(3)在旋转过程中,的值是否为定值?若是,请求出该定值;若不是,请说明理由;
(3)拓展延伸:设AE=t,△EPF面积为S,试确定S关于t的函数关系式;当S=4.2时,求所对应的t的值.
【分析】(1)根据矩形的性质找出∠B=∠C=90°,再通过角的计算得出∠BAP=∠CPD,由此即可得出△ABP∽△PCD;
(2)过点F作FH⊥PC于点H,根据矩形的性质以及角的计算找出∠B=∠FHP=90°、∠BEP=∠HPE,由此即可得出△BEP∽△HPE,根据相似三角形的性质,找出边与边之间的关系即可得出结论;
(3)分点E在AB和AD上两种情况考虑,根据相似三角形的性质找出各边的长度,再利用分割图形求面积法找出S与t之间的函数关系式,令S=4.2求出t值,此题得解.
解:(1)∵四边形ABCD为矩形,
∴∠B=∠C=90°,∴∠BAP+∠BPA=90°.
∵∠MPN=90°,∴∠BPA+∠CPD=90°,
∴∠BAP=∠CPD,∴△ABP∽△PCD.
故答案为:∽.
(2)是定值.如图3,过点F作FH⊥PC于点H,
∵矩形ABCD中,AB=2,
∴∠B=∠FHP=90°,HF=AB=2,
∴∠BPE+∠BEP=90°.
∵∠MPN=90°,
∴∠BPE+∠HPE=90°,
∴∠BEP=∠HPE,
∴△BEP∽△HPE,
∴,∵BP=1,
∴.
(3)分两种情况:
①如图3,当点E在AB上时,0≤t≤2.
∵AE=t,AB=2,
∴BE=2﹣t.
由(2)可知:△BEP∽△HPE,
∴,即,
∴HP=4﹣2t.
∵AF=BH=PB+BH=5﹣2t,
∴S=S矩形ABHF﹣S△AEF﹣S△BEP﹣S△PHF
=AB•AF﹣AE•AF﹣BE•PB﹣PH•FH
=t2﹣4t+5(0≤t≤2).
当S=4.2时,t2﹣4t+5=4.2,
解得:t=2±.
∵0≤t≤2,
∴t=2﹣;
②如图4,当点E在AD上时,0≤t≤1,过点E作EK⊥BP于点K,
∵AE=t,BP=1,
∴PK=1﹣t.
同理可证:△PKE∽△FCP,
∴,即,
∴FC=2﹣2t.
∴DF=CD﹣FC=2t,DE=AD﹣AE=5﹣t,
∴S=S矩形EKCD﹣S△EKP﹣S△EDF﹣S△PCF=CD•DE﹣EK•KP﹣DE•DF﹣PC•FC=t2﹣2t+5(0≤t≤1).
当S=4.2时,t2﹣2t+5=4.2,
解得:t=1±.
∵0≤t≤1,
∴t=1﹣.
综上所述:当点E在AB上时,S=t2﹣4t+5(0≤t≤2),当S=4.2时,t=2﹣;当点E在AD上时,S=t2﹣2t+5(0≤t≤1),当S=4.2时,t=1﹣.
11.(2016•龙东地区)已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为点E、F,点O为AC的中点.
(1)当点P与点O重合时如图1,易证OE=OF(不需证明)
(2)直线BP绕点B逆时针方向旋转,当∠OFE=30°时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.
【分析】(1)由△AOE≌△COF即可得出结论.
(2)图2中的结论为:CF=OE+AE,延长EO交CF于点G,只要证明△EOA≌△GOC,△OFG是等边三角形,即可解决问题.
图3中的结论为:CF=OE﹣AE,延长EO交FC的延长线于点G,证明方法类似.
解:(1)∵AE⊥PB,CF⊥BP,
∴∠AEO=∠CFO=90°,
在△AEO和△CFO中,
,
∴△AOE≌△COF,
∴OE=OF.
(2)图2中的结论为:CF=OE+AE.
图3中的结论为:CF=OE﹣AE.
如图2中的结论证明如下:
延长EO交CF于点G,
∵AE⊥BP,CF⊥BP,
∴AE∥CF,
∴∠EAO=∠GCO,
在△EOA和△GOC中,
,
∴△EOA≌△GOC,
∴EO=GO,AE=CG,
在Rt△EFG中,∵EO=OG,
∴OE=OF=GO,
∵∠OFE=30°,
∴∠OFG=90°﹣30°=60°,
∴△OFG是等边三角形,
∴OF=GF,∵OE=OF,
∴OE=FG,∵CF=FG+CG,
∴CF=OE+AE.
选图3的结论证明如下:
延长EO交FC的延长线于点G,
∵AE⊥BP,CF⊥BP,
∴AE∥CF,
∴∠AEO=∠G,
在△AOE和△COG中,
,
∴△AOE≌△COG,
∴OE=OG,AE=CG,
在Rt△EFG中,∵OE=OG,
∴OE=OF=OG,
∵∠OFE=30°,
∴∠OFG=90°﹣30°=60°,
∴△OFG是等边三角形,
∴OF=FG,
∵OE=OF,
∴OE=FG,
∵CF=FG﹣CG,
∴CF=OE﹣AE.
12.如图,在正方形ABCD中,点E为对角线AC上的一点,连接BE,DE.
(1)如图1,求证:△BCE≌△DCE;
(2)如图2,延长BE交直线CD于点F,G在直线AB上,且FG=FB.
①求证:DE⊥FG;
②已知正方形ABCD的边长为2,若点E在对角线AC上移动,当△BFG为等边三角形时,求线段DE的长(直接写出结果,不必写出解答过程).
【分析】(1)利用判定定理(SAS)可证;
(2)①利用(1)的结论与正方形的性质,只需证明∠FDE+∠DFG=90°即可;
②由DE⊥FG可构造直角三角形,利用等边三角形的性质及三角函数可求DE的长.
解:(1)∵四边形ABCD是正方形,AC是其对角线,
∴∠DCE=∠BCE,CD=CB
在△BCE与△DCE中,
∴△BCE≌△DCE(SAS).
(2)①证明:∵由(1)可知△BCE≌△DCE,
∴∠FDE=∠FBC
又∵四边形ABCD是正方形,
∴CD∥AB,
∴∠DFG=∠BGF,∠CFB=∠GBF,
又∵FG=FB,
∴∠FGB=∠FBG,
∴∠DFG=∠CFB,
又∵∠FCB=90°,
∴∠CFB+∠CBF=90°,
∴∠EDF+∠DFG=90°,
∴DE⊥FG
②解:如下图所示,
∵△BFG为等边三角形,
∴∠BFG=60°,
∵由(1)知∠DFG=∠CFB=60°,
在Rt△FCB中,∠FCB=90°,
∴FC=CB•cot60°=,DF=2﹣,
又∵DE⊥FG,
∴∠FDE=∠FED=30°,OD=OE,
在Rt△DFO中,
OD=DF•cos30°=﹣1,
∴DE=2(﹣1)
13.如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
【分析】(1)①由旋转的性质可知:AF=AG,∠DAF=∠BAG,接下来在证明∠GAE=∠FAE,然后依据SAS证明△GAE≌△FAE即可;②由全等三角形的性质可知:AB=AH,GE=EF=5.设正方形的边长为x,接下来,在Rt△EFC中,依据勾股定理列方程求解即可;
(2)将△ABM逆时针旋转90°得△ADM′.在△NM′D中依据勾股定理可证明NM′2=ND2+DM′2,接下来证明△AMN≌△ANM′,于的得到MN=NM′,最后再由BM=DM′证明即可.
解:(1)①由旋转的性质可知:AF=AG,∠DAF=∠BAG.
∵四边形ABCD为正方形,
∴∠BAD=90°.
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠FAE.
在△GAE和△FAE中,
∴△GAE≌△FAE.
②∵△GAE≌△FAE,AB⊥GE,AH⊥EF,
∴AB=AH,GE=EF=5.
设正方形的边长为x,则EC=x﹣2,FC=x﹣3.
在Rt△EFC中,由勾股定理得:EF2=FC2+EC2,即(x﹣2)2+(x﹣3)2=25.
解得:x=6.
∴AB=6.
∴AH=6.
(3)如图所示:将△ABM逆时针旋转90°得△ADM′.
∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°.
由旋转的性质可知:∠ABM=∠ADM′=45°,BE=DM′.
∴∠NDM′=90°.
∴NM′2=ND2+DM′2.
∵∠EAM′=90°,∠EAF=45°,
∴∠EAF=∠FAM′=45°.
在△AMN和△ANM′中,,
∴△AMN≌△ANM′.
∴MN=NM′.
又∵BM=DM′,
∴MN2=ND2+BM2.
14.如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF
于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)探究线段EG、GF、AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2,求BE的长.
【分析】(1)先依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF;
(2)连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF=GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FO•AF,于是可得到GE、AF、FG的数量关系;
(3)过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD﹣GH求解即可.
解:(1)证明:∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.
∴DG=GE=DF=EF.
∴四边形EFDG为菱形.
(2)EG2=GF•AF.
理由:如图1所示:连接DE,交AF于点O.
∵四边形EFDG为菱形,
∴GF⊥DE,OG=OF=GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴,即DF2=FO•AF.
∵FO=GF,DF=EG,
∴EG2=GF•AF.
(3)如图2所示:过点G作GH⊥DC,垂足为H.
∵EG2=GF•AF,AG=6,EG=2,
∴20=FG(FG+6),整理得:FG2+6FG﹣40=0.
解得:FG=4,FG=﹣10(舍去).
∵DF=GE=2,AF=10,
∴AD==4.
∵GH⊥DC,AD⊥DC,
∴GH∥AD.
∴△FGH∽△FAD.
∴,即=.
∴GH=.
∴BE=AD﹣GH=4﹣=.
15.如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3时,求线段DH的长.
【分析】(1)根据旋转变换的性质和全等三角形的判定定理证明△CAF≌△BAD,证明结论;
(2)①根据全等三角形的性质、垂直的定义证明即可;
②连接DF,延长AB交DF于M,根据题意和等腰直角三角形的性质求出DM、BM的长,根据勾股定理求出BD的长,根据相似三角形的性质列出比例式,计算即可得到答案.
解:(1)BD=CF.
理由如下:由题意得,∠CAF=∠BAD=θ,
在△CAF和△BAD中,
,
∴△CAF≌△BAD,
∴BD=CF;
(2)①由(1)得△CAF≌△BAD,
∴∠CFA=∠BDA,
∵∠FNH=∠DNA,∠DNA+∠NAD=90°,
∴∠CFA+∠FNH=90°,
∴∠FHN=90°,即BD⊥CF;
②连接DF,延长AB交DF于M,
∵四边形ADEF是正方形,AD=3,AB=2,
∴AM=DM=3,BM=AM﹣AB=1,
∵△ABC绕点A逆时针旋转45°,
∴∠BAD=45°,
∴AM⊥DF,
∴DB==,
∵∠MAD=∠MDA=45°,
∴∠AMD=90°,又∠DHF=90°,∠MDB=∠HDF,
∴△DMB∽△DHF,
∴=,即=,
解得,DH=.
16.如图1,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD、BC分别交于点E、F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.
(1)求证:①△DOK≌△BOG;②AB+AK=BG;
(2)若KD=KG,BC=4﹣.
①求KD的长度;
②如图2,点P是线段KD上的动点(不与点D、K重合),PM∥DG交KG于点M,PN∥KG交DG于点N,设PD=m,当S△PMN=时,求m的值.
【分析】(1)①先根据AAS判定△DOK≌△BOG,②再根据等腰三角形ABF和平行四边形AFKG的性质,得出结论BG=AB+AK;
(2)①先根据等量代换得出AF=KG=KD=BG,再设AB=a,根据AK=FG列出关于a的方程,求得a的值,进而计算KD的长;②先过点G作GI⊥KD,求得S△DKG的值,再根据四边形PMGN是平行四边形,以及△DKG∽△PKM∽△DPN,求得S△DPN和S△PKM的表达式,最后根据等量关系S平行四边形PMGN=S△DKG﹣S△DPN﹣S△PKM,列出关于m的方程,求得m的值即可.
解:(1)①∵在矩形ABCD中,AD∥BC
∴∠KDO=∠GBO,∠DKO=∠BGO
∵点O是BD的中点
∴DO=BO
∴△DOK≌△BOG(AAS)
②∵四边形ABCD是矩形
∴∠BAD=∠ABC=90°,AD∥BC
又∵AF平分∠BAD
∴∠BAF=∠BFA=45°
∴AB=BF
∵OK∥AF,AK∥FG
∴四边形AFGK是平行四边形
∴AK=FG
∵BG=BF+FG
∴BG=AB+AK
(2)①由(1)得,四边形AFGK是平行四边形
∴AK=FG,AF=KG
又∵△DOK≌△BOG,且KD=KG
∴AF=KG=KD=BG
设AB=a,则AF=KG=KD=BG=a
∴AK=4﹣﹣a,FG=BG﹣BF=a﹣a
∴4﹣﹣a=a﹣a
解得a=
∴KD=a=2
②过点G作GI⊥KD于点I
由(2)①可知KD=AF=2
∴GI=AB=
∴S△DKG=×2×=
∵PD=m
∴PK=2﹣m
∵PM∥DG,PN∥KG
∴四边形PMGN是平行四边形,△DKG∽△PKM∽△DPN
∴,即S△DPN=()2
同理S△PKM=()2
∵S△PMN=
∴S平行四边形PMGN=2S△PMN=2×
又∵S平行四边形PMGN=S△DKG﹣S△DPN﹣S△PKM
∴2×=﹣()2﹣()2,即m2﹣2m+1=0
解得m1=m2=1
∴当S△PMN=时,m的值为1
17.已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
【分析】(1)根据正方形的性质和全等三角形的判定定理证明△APE≌△CFE,根据全等三角形的性质证明结论;
(2)①根据正方形的性质、等腰直角三角形的性质解答;
②根据PE∥CF,得到=,代入a、b的值计算求出a:b,根据角平分线的判定定理得到∠HCG=∠BCG,证明∠AEC=∠ACB,即可求出∠AEC的度数.
解:(1)∵四边形ABCD和四边形BPEF是正方形,
∴AB=BC,BP=BF,
∴AP=CF,
在△APE和△CFE中,
,
∴△APE≌△CFE, ∴EA=EC;
(2)①∵P为AB的中点,
∴PA=PB,又PB=PE,∴PA=PE,
∴∠PAE=45°,又∠DAC=45°,
∴∠CAE=90°,即△ACE是直角三角形;
②
∵EP平分∠AEC,EP⊥AG,
∴AP=PG=a﹣b,BG=a﹣(2a﹣2b)=2b﹣a
∵PE∥CF,
∴=,即=,
解得,a=b;
作GH⊥AC于H,
∵∠CAB=45°,
∴HG=AG=×(2b﹣2b)=(2﹣)b,又BG=2b﹣a=(2﹣)b,
∴GH=GB,GH⊥AC,GB⊥BC,
∴∠HCG=∠BCG,
∵PE∥CF,
∴∠PEG=∠BCG,
∴∠AEC=∠ACB=45°.
∴a:b=:1;∴∠AEC=45°.
18.在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
(1)当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
【分析】(1)根据矩形的性质及角之间的关系证明△BOD′≌△AOC′;
(2)①先进行假设,然后根据平行四边形的性质及相似三角形比例关系即可得出答案;
②易证△BOD′≌△C′OA,则AC′=BD′,∠OBD′=∠OC′A≠∠OAC′,从而得出∠AMB=α.
(1)证明:在矩形ABCD中,AC=BD,OA=OC=AC,OB=OD=BD,
∴OA=OC=OB=OD,
又∵OD=OD′,OC=OC′,
∴OB=OD′=OA=OC′,
∵∠D′OD=∠C′OC,
∴180°﹣∠D′OD=180°﹣∠C′OC,
∴∠BOD′=∠AOC′,
∴在△BOD′和△AOC′中,
∴△BOD′≌△AOC′;
(2)解:①△AOC′∽△BOD′;理由如下:
∵在平行四边形ABCD中,OB=OD,OA=OC,
又∵OD=OD′,OC=OC′,
∴OC′=OA,OD′=OB,
∵∠D′OD=∠C′OC,
∴180°﹣∠D′OD=180°﹣∠C′OC,
∴∠BOD′=∠AOC′,
∴△BOD′∽△AOC′,
∴BD′:AC′=OB:OA=BD:AC,
∵AC=kBD,
∴AC′=kBD′,
∴△BOD′∽△AOC′;
②AC′=kBD′,∠AMB=α;
设BD′与OA相交于点N,
∴∠BNO=∠ANM,
∴180°﹣∠OAC′﹣∠ANM=180°﹣∠OBD′﹣∠BNO,即∠AMB=∠AOB=α,
综上所述,AC′=kBD′,∠AMB=α;
19.已知菱形ABCD的边长为1,∠ADC=60°,等边△AEF两边分别交DC、CB于点E、F.
(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点,求证:菱形ABCD对角线AC、BD的交点O即为等边△AEF的外心;
(2)若点E、F始终分别在边DC、CB上移动,记等边△AEF的外心为P. ①猜想验证:如图2,猜想△AEF的外心P落在哪一直线上,并加以证明;②拓展运用:如图3,当E、F分别是边DC、CB的中点时,过点P任作一直线,分别交DA边于点M,BC边于点G,DC边的延长线于点N,请你直接写出的值.
【分析】(1)连接OE、0F,由四边形ABCD是菱形,得出AC⊥BD,BD平分∠ADC,AD=DC=BC,又由E、F分别为DC、CB中点,证得0E=OF=OA,则可得点O即为△AEF的外心;
(2)①连接PE、PA,过点P分别作PI⊥CD于I,PJ⊥AD于J,求出∠IPJ的度数,又由点P是等边△AEF的外心,易证得△PIE≌△PJA,可得PI=PJ,即点P在∠ADC的平分线上,即点P落在直线DB上;
②连接BD、AC交于点P,由(1)可得点P即为△AEF的外心.设DM=x,DN=y(x≠0,y≠O),则CN=y﹣1,先利用AAS证明△GBP≌△MDP,得出BG=DM=x,CG=1﹣x,再由BC∥DA,得出△NCG∽△NDM,根据相似三角形对应边成比例得出=,进而求出为定值2.
(1)证明:如图1,连接OE、0F,
∵四边形ABCD是菱形,
∴AC⊥BD,BD平分∠ADC,AD=DC=BC,
∴∠COD=∠COB=∠AOD=90°.
∠ADO=∠ADC=×60°=30°,
又∵E、F分别为DC、CB中点,
∴OE=CD,OF=BC,AO=AD,
∴0E=OF=OA,
∴点O即为△AEF的外心;
(2)解:①猜想:外心P一定落在直线DB上.理由如下:
如图2,分别连接PE、PA,过点P分别作PI⊥CD于I,PJ⊥AD于J,
∴∠PIE=∠PJD=90°,
∵∠ADC=60°,
∴∠IPJ=360°﹣∠PIE﹣∠PJD﹣∠JDI=120°,
∵点P是等边△AEF的外心,
∴∠EPA=120°,PE=PA,
∴∠IPJ=∠EPA,
∴∠IPE=∠JPA,
∴△PIE≌△PJA,
∴PI=PJ,
∴点P在∠ADC的平分线上,即点P落在直线DB上;
②为定值2.
连接BD、AC交于点P,由(1)可得点P即为△AEF的外心.
如图3,设MN交BC于点G,
设DM=x,DN=y(x≠0,y≠O),则CN=y﹣1,
∵BC∥DA,
∴∠GBP=∠MDP,∠BGP=∠DMP,
又由(1)知BP=DP,
∴△GBP≌△MDP(AAS),
∴BG=DM=x,
∴CG=1﹣x.
∵BC∥DA,
∴△NCG∽△NDM,
∴=,
∴=,
∴x+y=2xy,
∴+=2,
即=2.
20.在正方形ABCD中,BD是一条对角线,点E在直线CD上(与点C,D不重合),连接AE,平移△ADE,使点D移动到点C,得到△BCF,过点F作FG⊥BD于点G,连接AG,EG.
(1)问题猜想:如图1,若点E在线段CD上,试猜想AG与EG的数量关系是 AG=EG ,位置关系是 AG⊥EG ;
(2)类比探究:如图2,若点E在线段CD的延长线上,其余条件不变,小明猜想(1)中的结论仍然成立,请你给出证明;
(3)解决问题:若点E在线段DC的延长线上,且∠AGF=120°,正方形ABCD的边长为2
,请在备用图中画出图形,并直接写出DE的长度.
【分析】(1)由平移得到EF=AD,再由正方形的性质得出∠ADG=∠CDB,DG=FG,从而证明△AGD≌△EGF即可;
(2)由平移得到EF=AD,再由正方形的性质得出∠ADG=∠CDB,DG=FG,从而证明△AGD≌△EGF即可;
(3)由(1)的结论AG=EG,AG⊥EG,得出∠GEA=45°,推导出∠AED=30°,再由三角函数即可求解.
解:(1)如图1,
由平移得,EF=AD,
∵BD是正方形的对角线,
∴∠ADB=∠CDB=45°,
∵CF⊥BD,
∴∠DGF=90°,
∴∠GFD+∠CBD=90°,
∴∠DFG=45°,
∴GD=GF,
在△AGD和△EGF中,
,
∴△AGD≌△EGF
∴AG=EG,∠AGD=∠EGF,
∴∠AGE=∠AGD+∠DGE=∠EGF+DGE=90°,
∴AG⊥EG.
故答案为AG=EG,AG⊥EG.
(2)(1)中的结论仍然成立,
证明:如图2
由平移得,EF=AD,
∵BD是正方形的对角线,
∴∠ADB=∠CDB=45°,
∵CF⊥BD,
∴∠DGF=90°,
∴∠GFD+∠CBD=90°,
∴∠DFG=45°,
∴GD=GF,
在△AGD和△EGF中,
,
∴△AGD≌△EGF
∴AG=EG,∠AGD=∠EGF,
∴∠AGE=∠AGD+∠DGE=∠EGF+DGE=90°,
∴AG⊥EG.
(3)由(1)有,AG=CG,AG⊥EG,
∴∠GEA=45°,
∵∠AGF=120°,
∴∠AGB=∠CGB,=30°,
∴∠FGE=∠CGB=∠CGE=30°,
∴∠CEG=75°,
∴∠AED=30°,
在Rt△ADE中,AD=2,
∴DE=2.
21.如图,正方形ABCD边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG=2时,求证:菱形EFGH为正方形;
(3)设AH=x,DG=2x,△FCG的面积为y,试求y的最大值.
【分析】(1)过F作FM⊥CD,垂足为M,连接GE,由AB与CD平行,利用两直线平行内错角相等得到一对角相等,再由GE为菱形的对角线,利用菱形的性质得到一对内错角相等,利用等式的性质即可得证;
(2)由于四边形ABCD为正方形,四边形HEFG为菱形,那么∠D=∠A=90°,HG=HE,而AH=DG=2,易证△AHE≌△DGH,从而有∠DHG=∠HEA,等量代换可得∠AHE+∠DHG=90°,易证四边形HEFG为正方形;
(3)欲求△FCG的面积,由已知得CG的长易求,只需求出GC边的高,通过证明△AHE≌△MFG可得.
(1)证明:过F作FM⊥CD,垂足为M,连接GE,
∵CD∥AB,∴∠AEG=∠MGE,
∵GF∥HE,∴∠HEG=∠FGE,
∴∠AEH=∠FGM;
(2)证明:在△HDG和△AEH中,
∵四边形ABCD是正方形,
∴∠D=∠A=90°,
∵四边形EFGH是菱形,
∴HG=HE,
在Rt△HDG和△AEH中,
,
∴Rt△HDG≌△AEH(HL),
∴∠DHG=∠AEH,
∴∠DHG+∠AHE=90°
∴∠GHE=90°,
∴菱形EFGH为正方形;
(3)解:过F作FM⊥CD于M,
在△AHE与△MFG中,,
∴△AHE≌△MFG,
∴MF=AH=x,∵DG=2x,
∴CG=6﹣2x,
∴y=CG•FM=•x•(6﹣2x)=﹣(x﹣)2+,
∵a=﹣1<0,∴当x=时,y最大=.
22.如图1,四边形ABCD中,AD∥BC,AB⊥BC,点E在边AB上,∠DEC=90°,且DE=EC.
(1)求证:△ADE≌△BEC;
(2)若AD=a,AE=b,DE=c,请用图1证明勾股定理:a2+b2=c2;
(3)线段AB上另有一点F(不与点E重合),且DF⊥CF(如图2),若AD=2,BC=4,求EF的长.
【分析】(1)首先得出∠ADE=∠CEB,再利用全等三角形的判定方法得出△ADE≌△BEC(AAS);
(2)利用梯形的面积和直角三角形面积公式求出答案;
(3)利用全等三角形的性质结合相似三角形的判定与性质得出AF的长,进而得出答案.
(1)证明:如图1,∵∠DEC=90°,
∴∠AED+∠CEB=90°,
∵∠ADE+∠AED=90°,
∴∠ADE=∠CEB,
在△ADE和△BEC中
,
∴△ADE≌△BEC(AAS);
(2) 证明:如图1,
∵AB⊥BC,∠DEC=90°,
∴△ADE,△DEC,△BEC都是直角三角形,
∵AD=a,AE=b,DE=c,且DE=EC,△ADE≌△BEC,
∴BE=a,BC=b,
∴(a+b)(a+b)=ab+c2+ab,
整理得:a2+b2=c2;
(3) 解:如图2,
由(1)得:△ADE≌△BEC(AAS),
则AD=BE=2,BC=AE=4,
∵DF⊥CF,∴∠AFD+∠BFC=90°,
∵∠BFC+∠BCF=90°,∴∠AFD=∠BCF,
又∵∠A=∠B,∴△AFD∽△BCF,
∴=,
设AF=x,则BF=6﹣x,
故=,
解得:x1=2,x2=4,
∵点F不与点E重合,
∴x=2,
∴EF=6﹣2﹣2=2.
23.如图1,正方形ABCD中,AC是对角线,等腰Rt△CMN中,∠CMN=90°,CM=MN,点M在CD边上,连接AN,点E是AN的中点,连接BE.
(1)若CM=2,AB=6,求AE的值;
(2)求证:2BE=AC+CN;
(3)当等腰Rt△CMN的点M落在正方形ABCD的BC边上,如图2,连接AN,点E是AN的中点,连接BE,延长NM交AC于点F.请探究线段BE、AC、CN的数量关系,并证明你的结论.
【分析】(1)根据正方形的性质和等腰直角三角形的性质知∠ACN=90°,运用勾股定理计算即可;
(2)延长NC与AB的延长线交于一点G,AC+CN转化为GN,运用三角形的中位线性质易得证;
(3)类比(2)易得BE=(AC﹣CN).
【解答】解:(1)
∵四边形ABCD是正方形,AB=6,
∴AC=6,
∵等腰Rt△CMN中,∠CMN=90°,CM=MN,CM=2,
∴CN=2,∵∠ACN=90°,
∴AN===4,
∵点E是AN的中点,
∴AE=2;
(2)如图①,延长NC与AB的延长线交于一点G,
则△ACG是等腰直角三角形,B为AG的中点,
∴AC=CG ∴GN=AC+CN,
∵点E是AN的中点,∴BE=GN
∴BE=AC+CN;
(3)BE=(AC﹣CN)
如图②,延长CN与AB的延长线交于一点G,
则△ACG是等腰直角三角形,B为AG的中点,
∴AC=CG,∴GN=AC﹣CN,
∵点E是AN的中点,
∴BE=GN,∴BE=(AC﹣CN).
24.正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.
(1)如图1,若点E是DC的中点,CH与AB之间的数量关系是 CH=AB ;
(2)如图2,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
(3)如图3,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.
【分析】(1)首先根据全等三角形判定的方法,判断出△ABF≌△CBE,即可判断出∠1=∠2;然后根据EH⊥BF,∠BCE=90°,可得C、H两点都在以BE为直径的圆上,判断出∠4=∠HBC,即可判断出CH=BC,最后根据AB=BC,判断出CH=AB即可.
(2)首先根据全等三角形判定的方法,判断出△ABF≌△CBE,即可判断出∠1=∠2;然后根据EH⊥BF,∠BCE=90°,可得C、H两点都在以BE为直径的圆上,判断出∠4=∠HBC,即可判断出CH=BC,最后根据AB=BC,判断出CH=AB即可.
(3)首先根据三角形三边的关系,可得CK<AC+AK,据此判断出当C、A、K三点共线时,CK的长最大;然后根据全等三角形判定的方法,判断出△DFK≌△DEH,即可判断出DK=DH,再根据全等三角形判定的方法,判断出△DAK≌△DCH,即可判断出AK=CH=AB;最后根据CK=AC+AK=AC+AB,求出线段CK长的最大值是多少即可.
解:(1)如图1,连接BE,,
在正方形ABCD中,
AB=BC=CD=AD,∠A=∠BCD=∠ABC=90°,
∵点E是DC的中点,DE=DF,
∴点F是AD的中点,
∴AF=CE,
在△ABF和△CBE中,
∴△ABF≌△CBE,
∴∠1=∠2,
∵EH⊥BF,∠BCE=90°,
∴C、H两点都在以BE为直径的圆上,
∴∠3=∠2,
∴∠1=∠3,
∵∠3+∠4=90°,∠1+∠HBC=90°,
∴∠4=∠HBC,
∴CH=BC,
又∵AB=BC,
∴CH=AB.
故答案为:CH=AB.
(2)当点E在DC边上且不是DC的中点时,(1)中的结论CH=AB仍然成立.
如图2,连接BE,
在正方形ABCD中,
AB=BC=CD=AD,∠A=∠BCD=∠ABC=90°,
∵AD=CD,DE=DF,
∴AF=CE,
在△ABF和△CBE中,
∴△ABF≌△CBE,
∴∠1=∠2,
∵EH⊥BF,∠BCE=90°,
∴C、H两点都在以BE为直径的圆上,
∴∠3=∠2,
∴∠1=∠3,
∵∠3+∠4=90°,∠1+∠HBC=90°,
∴∠4=∠HBC,
∴CH=BC,
又∵AB=BC,
∴CH=AB.
(3) 如图3,
∵CK≤AC+AK,
∴当C、A、K三点共线时,CK的长最大,
∵∠KDF+∠ADH=90°,∠HDE+∠ADH=90°,
∴∠KDF=∠HDE,
∵∠DEH+∠DFH=360°﹣∠ADC﹣∠EHF=360°﹣90°﹣90°=180°,
∠DFK+∠DFH=180°,∴∠DFK=∠DEH,
在△DFK和△DEH中,
∴△DFK≌△DEH,
∴DK=DH,
在△DAK和△DCH中,
∴△DAK≌△DCH,∴AK=CH
又∵CH=AB,∴AK=CH=AB,
∵AB=3,∴AK=3,AC=3,
∴CK=AC+AK=AC+AB=,
即线段CK长的最大值是.
25.问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F
分别在边BC、CD上,则当∠EAF与∠BAD满足 ∠BAD=2∠EAF 关系时,仍有EF=BE+FD.
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:=1.41,=1.73)
【分析】【发现证明】根据旋转的性质可以得到△ADG≌△ABE,则GF=BE+DF,只要再证明△AFG≌△AFE即可.
【类比引申】延长CB至M,使BM=DF,连接AM,证△ADF≌△ABM,证△FAE≌△MAE,即可得出答案;
【探究应用】利用等边三角形的判定与性质得到△ABE是等边三角形,则BE=AB=80米.把△ABE绕点A逆时针旋转150°至△ADG,只要再证明∠BAD=2∠EAF即可得出EF=BE+FD.
【发现证明】证明:如图(1),
∵△ADG≌△ABE,
∴AG=AE,∠DAG=∠BAE,DG=BE,
又∵∠EAF=45°,即∠DAF+∠BEA=∠EAF=45°,
∴∠GAF=∠FAE,
在△GAF和△FAE中,
,
∴△AFG≌△AFE(SAS),
∴GF=EF,
又∵DG=BE,
∴GF=BE+DF,
∴BE+DF=EF;
【类比引申】∠BAD=2∠EAF.
理由如下:如图(2),延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,
,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
故答案是:∠BAD=2∠EAF.
【探究应用】如图3,把△ABE绕点A逆时针旋转150°至△ADG,连接AF,过A作AH⊥GD,垂足为H.
∵∠BAD=150°,∠DAE=90°,
∴∠BAE=60°.
又∵∠B=60°,
∴△ABE是等边三角形,
∴BE=AB=80米.
根据旋转的性质得到:∠ADG=∠B=60°,
又∵∠ADF=120°,
∴∠GDF=180°,即点G在 CD的延长线上.
易得,△ADG≌△ABE,
∴AG=AE,∠DAG=∠BAE,DG=BE,
又∵AH=80×=40,HF=HD+DF=40+40(﹣1)=40
故∠HAF=45°,
∴∠DAF=∠HAF﹣∠HAD=45°﹣30°=15°
从而∠EAF=∠EAD﹣∠DAF=90°﹣15°=75°
又∵∠BAD=150°=2×75°=2∠EAF
∴根据上述推论有:EF=BE+DF=80+40(﹣1)≈109(米),即这条道路EF的长约为109米.
26.如图1,正方形OABC与正方形ODEF放置在直线l上,连结AD、CF,此时AD=CF.AD⊥CF成立.
(1)正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?若成立,请证明;若不成立,请说明理由.
(2)正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,求证:AD⊥CF.
(3)在(2)小题的条件下,AD与OC的交点为G,当AO=3,OD=时,求线段CG的长.
【分析】(1)根据正方形的性质,可得OA与OC的关系,OD与OF的关系,∠AOC与∠DOF的关系,根据等式的性质,可得∠AOD与∠COF的关系,根据SAS,可得三角形全等,根据全等三角形的性质,可得证明结论;
(2)根据全等三角形的性质、对顶角的性质,可得三角形的两个对应角相等,可得三角形相似,根据相似三角形的性质,可得证明结论;
(3)根据勾股定理,可得OE的长,根据根据正方形的性质,可得OM、OD、OE的关系,根据线段的和差,可得AM的长,根据同一个角的正切的两种表达方式,可得OG的长,再根据线段的和差,可得答案.
(1)解:AD=CF.
理由如下:
在正方形ABCO和正方形ODEF中,
AO=CO,OD=OF,∠AOC=∠DOF=90°,
∴∠AOC+∠COD=∠DOF+∠COD,(等式的性质)
即∠AOD=∠COF,
在△AOD和△COF中,
,
∴△AOD≌△COF(SAS),
∴AD=CF;
(2)证明:如图2,设AD与CF交于点H
∵△AOD≌△COF(SAS)∴∠OCF=∠GAO.
∵∠CGH=∠AGO,∴△AOG∽△CHG.
∴∠CHG=∠GOA=90°.∴AD⊥CF.
(3)解:如图,连接DF交OE于M,则DF⊥OE,DM=OM=OE,
∵正方形ODEF的边长为,由勾股定理得
∴OE==2,
∴DM=OM=OE×=1,
∴AM=AO+OM=3+1=4(线段的和差)
在Rt△ADM中,tan∠DAM=.
∴tan∠GAO=tan∠DAM=,
∴OG==
∴CG=OC﹣OG=3﹣=.
27如图,在正方形ABCD与等腰直角三角形BEF中,∠BEF=90°,BE=EF,连接PF,点P是FD的中点,连接PE、PC.
(1)如图1,当点E在CB边上时,求证:PE=CE;
(2)如图2,当点E在CB的延长线上时,线段PC、CE有怎样的数量关系,写出你的猜想,并给与证明.
【分析】(1)延长EP交DC于点G,由正方形的性质和已知条件可证明△PEF≌△PGD(AAS),进而可证明△CGE是等腰直角三角形,则CP⊥GE,CP=EG=PE,所以△CPE是等腰直角三角形.由等腰三角形的性质可得PE=CE,问题得证;
(2)PE=CE,延长EP交CD的延长线于点G,由(1)的证明思路即可证得.
解:(1)延长EP交DC于点G,如图(1)所示:
∵∠FEC=∠DCE=90°,
∴EF∥CD,
∴∠PFE=∠PDG,
又∵∠EPF=∠GPD,PF=PD,
∴在△PEF和△PGD中
∴△PEF≌△PGD(AAS),
∴PE=PG,EF=GD,
∵BE=EF,
∴BE=GD.
∵CD=CB,
∴CG=CE,
∴△CGE是等腰直角三角形,
∴CP⊥GE,CP=EG=PE,
∴△CPE是等腰直角三角形.
∴PE=CE;
(2)PE=CE,理由如下:如图(2)所示:
延长EP交CD的延长线于点G,
∵∠FEB+∠DCB=180°,
∴EF∥CD,
∴∠PEF=∠PGD,
又∵∠EPF=∠GPD,PF=PD,
∴在△PEF和△PGD中,
,
∴△PEF≌△PGD(AAS),
∴PE=PG,EF=GD,
∵BE=EF,∴BE=GD.
∵CD=CB,∴CG=CE,
∴△CGE是等腰直角三角形,
∴CP⊥GE,CP=EG=PE,
∴△CPE是等腰直角三角形.
∴PE=CE.
28.已知:l1∥l2∥l3∥l4,平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”.
(1)如图1,正方形ABCD为“格线四边形”,则正方形ABCD的边长为 .
(2)矩形ABCD为“格线四边形”,其长:宽=2:1,求矩形ABCD的宽.
(3)如图1,EG过正方形ABCD的顶点D且垂直l1于点E,分别交l2,l4于点F,G.将∠AEG绕点A顺时针旋转30°得到∠AE′D′(如图2),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′,C′分别在直线l2,l4上,求菱形AB′C′D′的边长.
【分析】(1)利用已知得出△AED≌△DGC(AAS),即可得出AE,以及正方形的边长;
(2)如图2过点B作BE⊥L1于点E,反向延长BE交L4于点F,则BE=1,BF=3,由四边形ABCD是矩形,∠ABC=90°,∠ABE+∠FBC=90°,根据∠ABE+∠EAB=90°,得到∠FBC=∠EAB,然后分类讨论,求得矩形的宽.
(3)首先过点E′作ON垂直于l1分别交l1,l2于点O,N,∠AEO=30°,则∠ED′N=60°,可求出AE=1,EO,EN,ED′的长,进而由勾股定理可知菱形的边长.
解:(1)
∵l1∥l2∥l3∥l4,∠AED=90°
∴∠DGC=90°,
∵四边形ABCD为正方形
∴∠ADC=90°,AD=CD,∵∠ADE+∠2=90°,
∴∠1+∠2=90°,∴∠1=∠ADE,
∵l3∥l4,∴∠1=∠DCG,
∠ADE=∠DCG,
在△AED与△DGC中,
,
∴△AED≌△GDC(AAS),
∴AE=GD=1,ED=GC=3,
∴AD==,
故答案为:;
(2)如图2过点B作BE⊥L1于点E,反向延长BE交L4于点F,
则BE=1,BF=3,
∵四边形ABCD是矩形,
∴∠ABC=90°,∴∠ABE+∠FBC=90°,
∵∠ABE+∠EAB=90°,∴∠FBC=∠EAB,
当AB<BC时,AB=BC,
∴AE=BF=,
∴AB==;
如图3当AB>BC时,
同理可得:BC=,
∴矩形的宽为:,;
(3)如图4过点E′作ON垂直于l1分别交l1,l4于点O,N,
∵∠OAE′=30°,则∠E′FN=60°
∵AE′=AE=1,
故E′O=,E′N=,E′D′=,
由勾股定理可知菱形的边长为:==.
29.正方形ABCD边长为4cm,点E,M分别是线段AC,CD上的动点,连接DE并延长,交正方形ABCD的边于点F,过点M作MN⊥DF于H,交AD于N.
(1)如图1,若点M与点C重合,求证:DF=MN;
(2)如图2,若点M从点C出发,以1cm/s的速度沿CD向点D运动,点E同时从点A出发,以cm/s速度沿AC向点C运动,运动时间为t(t>0);
①当点F是边AB的中点时,求t的值;
②连结FM,FN,当t为何值时△MNF是等腰三角形(直接写出t值).
【分析】(1)先判定△ADF≌△DNC,即可得到结论;
(2)①当点F是AB中点时,由比例式,计算即可,②先表示出AF,DN=CM=t,AN=DM=4﹣t,再分三种情况计算.
证明:(1)∵∠DNC+ADF=90°,∠DNC+∠DCN=90°,
∴∠ADF=∠DCN,
在△ADF和△DNC中
,
∴△ADF≌△DNC,∴DF=MN;
(2)①当点F是AB中点时,
∴AF=AB=2,
由题意可知,CM=t,AE=t,CE=4﹣t,
∵AB∥CD,
∴,∴,
∴t=,
②∵△AEF∽△CED,
∴,∴,
∴AF=,
∵△MND∽△DFA,
∴,∴,
∴DN=CM=t,AN=DM=4﹣t,
∵△MNF是等腰三角形,
Ⅰ、当FN=FM,
∵MN⊥DF,∴FD是MN的垂直平分线,
∴DN=DM,∴t=4﹣t,
∴t=2(此时点F与点B重合),
Ⅱ、当FM=MN时,点F在BC上,如图1,
∵∠NDM=∠MCF,ND=MC,FM=MN,
∴△MFC≌△NMD,∴FC=DM=4﹣t,
∵△NDM∽△DCF,
∴,
∴,
∴t=4(此时点F与点C重合),
Ⅲ、当FN=MN时,如图2,
∵∠FAN=∠NDM,AN=DM,FN=MN,
∴△FAN≌△NDM,∴AF=DN,
∴=t,∴t=0(舍),
即:当t=2或t=4时,△MNF是等腰三角形.
30.已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边长分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.
(1)如图①,当∠MAN点A旋转到BM=DN时,请你直接写出AH与AB的数量关系: AH=AB ;
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;
(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.
【分析】(1)由三角形全等可以证明AH=AB,
(2)延长CB至E,使BE=DN,证明△AEM≌△ANM,能得到AH=AB,
(3)分别沿AM、AN翻折△AMH和△ANH,得到△ABM和△AND,然后分别延长BM和DN交于点C,得正方形ABCE,设AH=x,则MC=x﹣2,NC=x﹣3,在Rt△MCN中,由勾股定理,解得x.
解:(1)如图①AH=AB,
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
在△ABM与△ADN中,,
∴△ABM≌△ADN,
∴∠BAM=∠DAN,AM=AN,
∵AH⊥MN,
∴∠MAH=MAN=22.5°,
∵∠BAM+∠DAN=45°,∴∠BAM=22.5°,
在△ABM与△AHM中,,
∴△ABM≌△AHM,∴AB=AH;
故答案为:AH=AD;
(2)数量关系成立.如图②,延长CB至E,使BE=DN.
∵ABCD是正方形,
∴AB=AD,∠D=∠ABE=90°,
在Rt△AEB和Rt△AND中,,
∴Rt△AEB≌Rt△AND,
∴AE=AN,∠EAB=∠NAD,
∴∠EAM=∠NAM=45°,
在△AEM和△ANM中,,
∴△AEM≌△ANM,
∴S△AEM=S△ANM,EM=MN,
∵AB、AH是△AEM和△ANM对应边上的高,
∴AB=AH;
(3)如图③分别沿AM、AN翻折△AMH和△ANH,得到△ABM和△AND,
∴BM=2,DN=3,∠B=∠D=∠BAD=90°,
分别延长BM和DN交于点C,得正方形ABCD,
由(2)可知,AH=AB=BC=CD=AD,
设AH=x,则MC=x﹣2,NC=x﹣3,
在Rt△MCN中,由勾股定理,得MN2=MC2+NC2,
∴52=(x﹣2)2+(x﹣3)2,
解得x1=6,x2=﹣1(不符合题意,舍去)
∴AH=6.